3种水文模型在淮河息县流域洪水模拟中的比较
2013-04-17李致家
邓 鹏,李致家
(1.南京信息工程大学水文气象学院,江苏南京 210044;2.河海大学水文水资源学院,江苏 南京 210098)
流域水文模型作为一种数学模型,它从定量上分析流域出口断面流量过程线形成的全部过程[1-2]。传统流域水文模型大多数是集总式概念性模型。分布式水文模型从提出至今经过近40 a的发展,逐渐显示出了它的理论意义和具有挑战性的应用价值[3-4]。在当前条件下,大部分的分布式模型采用概念性模型的方法,只是模型参数是分布式的。大多数分布式水文模型的一个显著特点是同DEM相结合,TOPMODEL就是在DEM基础上建立的最具代表性的模型[5-6]。常见的分布式水文模型主要有SHE模型、TOPKAPI模型[7-9]、SWAT模型[10]等。本文根据流域水文模型的发展过程,选用3种具有代表性的水文模型:新安江模型、TOPMODEL模型和SWAT模型,对淮河息县流域进行洪水模拟,比较这3种模型在该流域的适用性及特点。这3种模型分别代表了概念性模型、半分布式模型和分布式模型。
1 模型简介
1973年赵人俊[11]建立了国内第一个完整的流域水文模型——新安江模型,它是目前国内应用最广泛的流域水文模型之一,是一种分散参数的概念性模型。三水源新安江模型蒸散发计算采用三层模型;产流计算采用蓄满产流模型;用自由蓄水库结构将总径流划分为地表径流、壤中流和地下径流;流域汇流计算采用线性水库;河道汇流采用马斯京根分段连续演算或滞后演算法。1979年,Beven等[5]提出了以变源产流为基础的TOPMODEL模型。该模型主要借助地形指数ln(a/tanβ)来描述和解释径流趋势以及下垫面的空间变化对流域水文循环过程的影响。基于重力作用导致径流沿坡向运动的原理,模拟了径流产生的变动产流面积,尤其是地表或地下饱和水源面积的变动。该模型结构简单,参数较少。SWAT模型是由美国农业部开发的流域尺度分布式模型,可用来模拟预测在具有多种土壤类型、土地利用和管理条件的复杂大流域中,土地管理措施对水、沙、化学物质等的长期影响。SWAT模型是基于物理过程的模拟模型,其主要输入要素包括气象、水文、土壤特性、植被覆盖、化学物质和土地利用情况等,计算效率较高,可以模拟和研究长期的变化过程。

图1 息县流域水系示意图Fig.1 Sketch map of stream networKof Xixian Basin
2 应用与比较
2.1 流域简介
息县以上流域位于河南省南部,居淮河上游。息县水文站控制面积10190 km2,干流河长250km,主要的支流有浉河、竹竿河和清水河,在浉河和竹竿河支流小潢河上分别建有南湾(集水面积1058 km2)和石山口(集水面积306 km2)2座大型水库,扣除2座大型水库后息县以上的集水面积为8 826 km2,其中南湾水库多年平均年入库水量约占息县水文站多年平均年来水量的10%(图1)。息县水文站断面一般宽700~800 m,最大测流断面宽2470 m,最大水深10.50 m。
该流域处于北亚热带和暖温带,在气候上具有过渡特征。汛期降雨受季风影响,一般每年四五月份雨量开始逐渐增多,随着江淮流域进入梅雨季节,6月上中旬汛期开始。多年平均年降雨量1060 mm,其中50%左右的降雨集中在汛期(6—9月),多年平均气温在14~16℃之间。流域内地形呈现西高东低趋势,高程范围在15~982 m之间,平均高程142 m。流域辖区的中山区、低山区、丘陵区主要土壤类型为黄棕壤土类,土体有明显的黏化过程,呈酸性或微酸性,生长有松、衫等针叶和阔叶林,以及漆树、油桐、油茶等经济林木。在中山、低山、岗丘及河谷等各种地貌类型的农田主要种植稻、麦、油菜等农作物。
2.2 资料情况及处理
流域的数字高程数据资料可从美国国家航空航天局(NASA)提供的30 m精度ASTER全球数字高程模型获得[12],从美国马里兰大学(UMD)网站可以下载全球相当于1 km尺度的土地利用网格资料[13],从NASA的全球土地资料同化系统(GLDAS)中可以获取相当于10 km尺度的土壤类型资料[14],由DEM采用GIS软件可以提取息县以上流域模拟水系及流域边界。淮河息县以上流域的地形和DEM模拟生成的水系、土地利用和土壤类型分别见图2~4。
根据流域内的测站分布情况,搜集了桐柏、黄岗、大坡岭等13个雨量站1985—2006年的雨量资料、息县水文站的流量资料以及2座水库的出库流量资料,时段长为1 h,同时转化为以日为时段的资料;搜集了信阳、驻马店、固始气象站1951—2007年以日为时段的各种气象资料,包括日最高和最低气温、降水、风速、湿度、日照时数等,资料站点的分布情况如图5所示。

图2 息县流域DEM及模拟水系Fig.2 DEM and drainage networKof Xixian Basin

图3 息县流域土地利用分布Fig.3 Land use of Xixian Basin
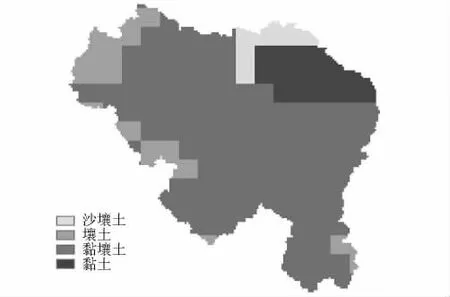
图4 息县流域土壤类型分布Fig.4 Soil types of Xixian Basin
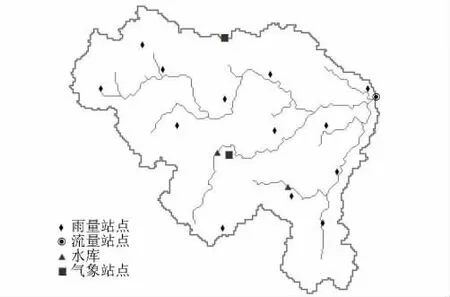
图5 息县流域资料站点分布Fig.5 Gauge stations of Xixian Basin
2.3 应用
新安江模型、TOPMODEL模型及SWAT模型的应用中,都是利用1985—1997年的资料进行模型参数率定,用1998—2006年的资料进行参数检验。新安江模型的应用中,根据雨量站的分布采用泰森多边形法将流域分为13个子流域,计算每个子流域的产流及汇流,再用马斯京根法进行河道汇流计算,演算到流域出口,同时将水库出流也演算至流域出口并叠加,得到流域出口的流量过程。
TOPMODEL模型应用中,划分子流域的方法以及水库出流的处理方法与新安江模型应用的方法相同。计算每个子流域的地形指数分布曲线,进而计算产流过程,子流域的汇流计算采用基于地形的等流时线法。
SWAT模型应用中,使用的是最新的ArcSWAT2009[15]。按水系分布情况将流域划分为23个子流域,每个子流域再按土地利用状况、土壤特性以及坡度划分为若干个水文响应单元(HRU)。对率定期资料进行参数敏感性分析,并对主要的敏感性参数进行自动率定,将率定好的SWAT模型再应用于检验期资料。对各场洪水模拟计算结果特征值比较如表1所示,洪水模拟与实测过程线比较如图6所示。
2.4 比较与讨论
2.4.1 模型结构比较
在产流计算中,新安江模型采用的是经验性的蓄水容量曲线来分配水量,从而得到产流量。TOPMODEL模型采用的是地形指数曲线来模拟变动的饱和区从而得到产流量。新安江模型和TOPMODEL模型在模拟饱和区水量的方法上具有相似性,并且蓄水容量曲线与地形指数曲线在原理上具有相通性[16-17]。所不同的是,地形指数曲线可以根据地形关系计算得到,具有一定的物理基础,而蓄水容量曲线参数需要人为率定[18],因而TOPMODEL模型作为一种半分布式模型,结合了地形信息,所需率定的参数比新安江模型少,是TOPMODEL模型的优点之一。TOPMODEL模型按照地下水面深在空间上的分布及变化判断出源面积,并将壤中流和饱和坡面流分别计算,最后汇总到流域总径流中。与此相反,新安江模型是先计算出总径流量,然后通过自由水蓄水库结构划分成地表径流、壤中流和地下径流,以供接下来的汇流计算。它们的产流计算模式都可以看作是蓄满产流,但是TOPMODEL模型可以具体分析流域产流面积的位置和分布,而新安江模型只是将整个流域的产流过程用一条蓄水容量曲线来描述。

表1 洪水模拟特征值比较Table 1 Comparison of characteristic values for simulation of floods

图6 洪水模拟与实测过程线比较Fig.6 Comparison of simulated and observed flood processes
TOPMODEL模型作为一种半分布式模型,以地形指数值来反映流域各点的水文属性,地形指数值相同或相似的点可以归为同类流域区域,并将其作为计算单元。SWAT模型是以HRU为计算单元,SWAT模型的HRU分配考虑因素比TOPMODEL模型多,包括土地利用、土壤属性、坡度等,所以与TOPMODEL模型相比,SWAT模型是一种综合考虑流域各种信息的分布式水文模型,其结构和参数比TOPMODEL模型及新安江模型要复杂很多。
2.4.2 汇流方法比较
汇流计算方法对模拟结果起着重要影响。新安江模型根据已划分好的3种水源,采用线性水库的概念分别进行汇流计算,得到计算单元的径流过程,这是一种概念性的方法,各种汇流参数需要人为率定。TOPMODEL模型则是根据以地形为基础的等流时线法进行汇流,与新安江模型相比,它结合了地形信息去考虑汇流过程,率定参数少,并且结合了一定的实际物理意义。SWAT模型的汇流方法采用水力学计算方法,这也是大部分代表前沿性分布式水文模型应当研究和采取的汇流计算方法。这3种模型的汇流计算方法也代表了从简单到复杂、从经验关系到物理过程的这样一种发展趋势。
2.4.3 应用结果比较
新安江模型作为一种分散参数的概念性模型,采用划分子流域的方法考虑下垫面的不均匀性,其模拟结果很好。TOPMODEL模型在洪水模拟中设置了针对每场洪水都可调试的植被根系层初始水含量参数,模拟结果很好,并且其参数少、结构简单,特别适用于湿润地区[19-21]。SWAT模型作为分布式模型,充分考虑了流域的各种下垫面信息,并且尽量根据物理基础去描述水流运动及其变化规律,可以得到较好的结果,但是其结果比新安江模型和TOPMODEL模型结果略差。以上结果从图6亦可见一斑。分布式水文模型尽管结构复杂、考虑全面,但对于河道断面的洪水预报而言,其应用效果不一定比传统概念性或半分布式水文模型好。产生这种现象的一个原因可能是分布式模型考虑因素众多,反而将各种误差叠加放大了,而结构简单的概念性模型或半分布式模型反而在误差积累问题上更具优势[22]。然而分布式水文模型代表了模型研究的前沿方向,它为深入仔细地探求水文运动及其变化规律打下基础,并且通过分布式模型可以研究某些具体要素对水文循环及其运动规律的影响,做到了水文模型模拟的精细化。
3 结 语
本文将具有代表性的3种水文模型应用于淮河息县流域的洪水过程模拟中,得到较好的结果。这3种模型也代表了水文模型从简单到复杂、从概念性到具有物理基础、从集总式到分布式的发展过程。在结果比较中发现新安江模型和TOPMODEL模型结果好于SWAT模型,说明在洪水过程模拟中,结构复杂、考虑全面的分布式模型的模拟结果并不一定优于传统的概念性或半分布式模型。然而分布式模型的最大优点不在于洪水过程模拟,而是其做到了模拟过程的精细化,考虑因素更加全面,代表了水文模型发展的前沿方向。例如在当前各种气候变化或覆被变化对水文过程影响的研究中,SWAT模型可以作为各种因素对水文过程变化研究的工具,也可以对其他各种要素如泥沙运动、河道化学物质的变化过程进行模拟。而新安江模型和TOPMODEL模型的结构简单、参数较少、应用方便,对洪水过程模拟的结果精度较高,得到广泛的应用。
这3种模型各有自己的优缺点,因而可以考虑如何采用集合预报的方法取长补短,提高模拟精度。例如美国国家海洋和大气管理局(NOAA)在对北美径流的模拟和预测中,采用多种模型模拟结果取均值的方法进行集合预报。这里也可考虑根据模型特点及应用流域特征,采用加权方法对模拟结果进行优化集合,相关方法有待于进一步研究。
[1]包为民.水文预报[M].北京:水利水电出版社,2006:139-142.
[2]李致家.水文模型的应用与研究[M].南京:河海大学出版社,2008:3-12.
[3]熊立华,郭生练.分布式流域水文模型[M].北京:水利水电出版社,2004:3-18.
[4]董李勤,章光新.全球气候变化对湿地生态水文的影响研究综述[J].水科学进展,2011,22(3):429-436.(DONG Liqin,ZHANG Guangxin.Review of the impacts of climate change on wetland ecohydrology[J].Advances in Water Science,2011,22(3):429-436.(in Chinese))
[5]BEVEN KJ,KIRKBY M J.A physically based variable contributing area model of basin hydrology[J].Hydrological Science Bulletin,1979,24(1):43-69.
[6]SINGH V P.Computer models of watershed hydrology[M].Highlands Ranch Colorado,USA:Water Resources Publications,1995:627-668.
[7]刘志雨.基于GIS的分布式托普卡匹水文模型在洪水预报中的应用[J].水利学报,2004,35(4):70-75.(LIU Zhiyu.Application of GIS-based distributed hydrological model to flood forecasting[J].Journal of Hydraulic Engineering,2004,35(4):70-75.(in Chinese))
[8]赵君,张晓民.改进的TOPKAPI模型及其在洪水预报中的应用[J].河海大学学报:自然科学版,2011,39(2),131-136.(ZHAO Jun,ZHANG Xiaomin.Application of improved TOKAPI model to flood forecast[J].Journal of Hohai University:Natural Sciences,2011,39(2),131-136.(in Chinese))
[9]DENG Peng,LI Zhijia,LIU Zhiyu.Numerical algorithm of distributed TOPKAPI model and its application[J].Water Science and Engineering,2008,1(4):14-21.
[10]李晓,李致家,董佳瑞.SWAT模型在伊河上游径流模拟中的应用[J].河海大学学报:自然科学版,2009,37(1):23-26.(LI Xiao,LI Zhijia,DONG Jiarui.Application of SWAT model in runoff simulation in upper reaches of Yihe River[J].Journal of Hohai University:Natural Sciences,2009,37(1):23-26.(in Chinese))
[11]赵人俊.流域水文模拟:新安江模型与陕北模型[M].北京:水利电力出版社,1984:106-130.
[12]NASA.ASTER global digital elevation model 002[EB/OL].[2011-12-05].https://wist.echo.nasa.gov/api/.
[13]UMD.1km Global land cover[EB/OL].[2010-05-04].http://www.geog.umd.edu/landcover/1km-map/meta-data.html.
[14]NASA.GLDASglobal soils dataset of Reynolds[EB/OL].[2010-05-04].http://www.ngdc.noaa.gov/.
[15]SWAT.Soil and water assessment tool[EB/OL].[2012-01-09].http://swatmodel.tamu.edu/.
[16]董小涛,李致家,李利琴.不同水文模型在半干旱地区的应用比较研究[J].河海大学学报:自然科学版,2006,34(2),132-135.(DONG Xiaotao,LI Zhijia,LI Liqin.Application and comparison of three hydrological models in semi-arid region[J].Journal of Hohai University:Natural Sciences,2006,34(2),132-135.(in Chinese))
[17]SIVAPALAN M,WOODSR A,KALMA J D.Variable bucket representation of TOPMODEL and investigation of the effects of rainfall heterogeneity[J].Hydrological Processes,1997,11:1307-1330.
[18]戴建男,李致家,黄鹏年,等.新安江模型参数不确定性分析[J].河海大学学报:自然科学版,2011,39(6):618-622.(DAI Jiannan,LI Zhijia,HUANG Pengnian,et al.Uncertainty analysis of Xin’anjiang model parameters[J].Journal of Hohai University:Natural Sciences,2011,39(6):618-622.(in Chinese))
[19]DENG Peng,LI Zhijia,XIE Fan.Application of TOPMODEL in Buliu River Basin and comparison with Xin'anjiang model[J].Water Science and Engineering,2008,1(2):25-32.
[20]邓鹏,李致家,谢帆.TOPMODEL在珠江流域布柳河流域的应用及其与新安江模型的比较[J].湖泊科学,2009,21(3):441-444.(DENG Peng,LI Zhijia,XIE Fan.Application of TOPMODEL in Buliu River catchment,Pearl River basin and comparison with Xin’anjiang model[J].Journal of Lake Sciences,2009,21(3):441-444.(in Chinese))
[21]谢帆,李致家,姚成.TOPMODEL 和新安江模型的应用比较[J]. 水力发电,2007,33(10):14-18.(XIEFan,LI Zhijia,YAO Cheng.The application and comparative study of TOPMODEL and Xin’anjiang model[J].Water Power,2007,33(10):14-18.(in Chinese)).
[22]叶金印,姚成,李京兵,等.综合误差系数在新安江模型参数全局优化中的应用[J].河海大学学报:自然科学版,2013,41(1):1-5.(YE Jinyin,YAO Cheng,LI Jingbing,et al.Application of comprehensive error coefficient to global parameter optimization in Xin’anjiang model[J].Journal of Hohai University:Natural Sciences,2013,41(1):1-5.(in Chinese))
