坝基岩体力学参数的PSO-ABAQUS联合反演

韩 峰，徐 磊，张太俊

(1.浙江省水利水电勘测设计院，浙江杭州 310002;2.河海大学水利水电学院，江苏 南京 210098)

各类坝基岩体都是在漫长地质历史中形成的天然地质体，在给定力学模型的前提下，合理确定其力学参数是开展坝体-坝基系统应力变形分析及稳定性评价并取得合理成果的关键之一［1］。坝基岩体力学参数的确定一般采用试验与工程类比相结合的方法，但由于坝基岩体固有的复杂性和不确定性，基于这一方法所确定的力学参数往往与实际情况不符，导致了以岩体为基础的坝工设计分析成果与实际情况不符。随着计算机、现代监测仪器和监测技术、岩石力学理论和数值计算方法的不断发展、应用，基于实测变形资料的力学参数反演分析方法逐渐成为解决这一问题的有效手段［2-4］。坝基岩体力学参数的反演本质上是一个相关参数的寻优过程，因而如何选择一个高效的优化算法是其核心问题之一［5］。自20世纪80年代以来，相关学者提出并发展了一些区别于传统优化方法的智能优化算法，如人工神经网络(ANN)法、蚁群算法(ACO)、遗传算法(GA)及粒子群优化算法(PSO)等，其中，PSO算法因其收敛快、鲁棒性好、隐含并行性及易于实现［6］等特点，一经出现即得到了很快的发展。目前，已有相关学者将PSO算法应用于初始地应力场反演等诸多领域，效果良好［7-12］。

笔者将PSO算法引入坝基岩体力学参数反演领域，并提出基于PSO算法［13］和ABAQUS的坝基岩体力学参数联合反演法。在介绍粒子群优化算法基本理论的基础上，构建了坝基岩体力学参数的数学反演模型，给出了具体的实施流程并开发了相应的程序，实现了基于施工和运行期实测变形资料的坝基岩体力学参数PSO-ABAQUS联合反演。算例分析表明，所提出的联合反演法不仅简便易行，而且反演效率较高，是一种合理确定坝基岩体力学参数的通用方法。

1 坝基岩体力学参数的反演模型

反演分析按照所采用方法的不同，总体上可以分为正反分析法和逆反分析法两大类。在坝基岩体力学参数反演领域，由于所涉及的研究对象为具有复杂工程特性的天然地质体，因此通常不具备采用逆反分析法进行参数反演的前提条件，故笔者采用正反分析法开展参数反演。

对于正反分析法，基于实测变形数据(通常为实测位移)的坝基岩体力学参数反演本质上是一个数学优化问题，待反演的力学参数即为此优化问题的设计变量，寻优过程即为寻找满足目标函数极小的一组参数来使得正演分析的计算结果(通常采用有限元法)与监测数据一致。

在坝工建设和运行过程中，通过布置各类监测仪器，可以获取包括坝体应力、变形在内的多种监测资料。理论上，监测资料都可以作为坝基岩体力学参数反演分析的基础信息，但考虑到监测资料的精度以及待反演参数对监测资料的敏感性，目前在坝基岩体力学参数反演分析中，大多选取实测位移作为反演分析的基础信息［14］，鉴于此，本文所建立的坝基岩体力学参数反演模型中亦选择实测位移资料作为基础反演信息。

基于数学优化基本理论，建立坝基岩体力学参数反演数学模型:

其中

式中:φ(X)——目标函数;X——m维反演参数向量，具体的反演参数需在地质调查分析的基础上确定;hi(X)=0——第i个等式约束;gj(X)≤0——第j个不等式约束;N——位移实测点数目;M——位移分量数目;U'pq(X)——与反演参数向量X对应的第p测点的计算位移值;Upq——第p个测点的实测位移值。

对于待反演参数的一组特定取值，一般首先采用有限单元法来求解与之相对应的位移场，进而提取测点处的位移值。

在基于PSO算法的坝基岩体力学参数反演中，计算量最大的部分是每一组试算力学参数所对应的正演计算以及后续目标函数值(各粒子适应值)的计算，正演计算模型通常都很复杂，且计算规模很大，因而选择一个功能强大且通用的正演分析计算工具十分必要。考虑到通用有限元软件平台ABAQUS的适用性和计算效率［15］，本文采用ABAQUS作为正演分析的计算工具。

2 PSO算法

PSO算法是1995年由Kennedy和Eberhart提出的一种群体智能优化算法［13］。在PSO算法中，优化问题的每一个潜在解都是搜索空间中的一个粒子，若干个粒子构成一个粒子群。粒子的适应度即为被优化问题的目标函数值。每个粒子都具有位置和速度2个特征，位置决定粒子的适应度，而速度决定下一代粒子运动的方向和距离。在迭代过程中，粒子通过跟踪个体极值pBest和全局极值gBest实现代际更新，直到在整个搜索空间中找到最优解或达到最大迭代次数为止。

假设在一个m维的搜索空间中，由n个粒子构成一个粒子群X'={x1，…，xa，…，xn}，其中，第a个粒子的位置为 xa={xa1，xa2，…，xam}T，速度为 va={va1，va2，…，vam}T，其个体极值为 pa={pa1，pa2，…，pam}T，全局极值为pg={pg1，pg2，…，pgm}T，则第a个粒子的速度和位置按式(2)、式(3)完成代际更新。

式中:k——粒子更新代数;wk——惯性权重，控制PSO算法的搜索能力，wk取值较大，则全局寻优能力强，局部寻优能力弱，wk通常依代数的增加而线性递减;rand()——均匀分布于(0，1)之间的随机数;c1，c2——加速常数，均可取为2.0。式(2)右边第1部分为粒子先前行为的惯性;第 2部分为“认知(cognition)”部分，表示粒子本身的思考;第3部分为“社会(social)”部分，表示粒子间的信息共享与相互合作。

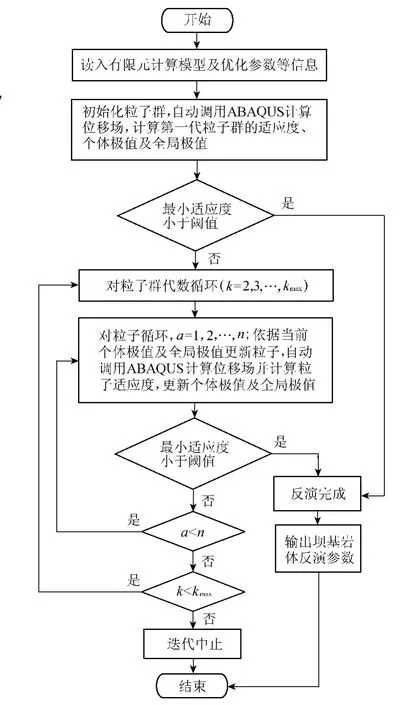
图1 PSO-ABAQUS联合反演程序流程Fig.1 Flow chart of PSO and ABAQUS combined inversion

3 程序开发及流程图

在第1节、第2节的基础上，笔者提出了坝基岩体力学参数的PSO-ABAQUS联合反演法，并编制了相应的FORTRAN计算程序。该程序在获取有限元计算模型及优化参数等相关信息的基础上，首先采用随机方法形成初始粒子群，然后基于每个粒子的位置，自动生成用以计算应力场的INP文件并调用ABAQUS求解器来完成坝体-坝基系统的应力变形分析，进而计算粒子的适应度(即目标函数值)，最后基于PSO算法完成粒子更新，直至找到符合预定最小阈值的最优粒子或达到最大迭代次数为止。若达到最大迭代次数仍未收敛，可调整反演模型或增加最大迭代次数，再次运行反演程序。图1为PSO-ABAQUS联合反演程序流程。

4 算例分析

为了验证本文所提PSO-ABAQUS联合反演法的有效性其相应FORTRAN程序的正确性，进行如下算例分析。假定一建于均质岩基上的重力坝，坝高为50 m，坝顶宽10 mm，坝底宽40 mm。建立此重力坝的有限元模型(图2)，模型共划分平面应变四结点四变形等参数单元337个，结点380个。在有限元计算模型中选取坝顶上、下游，坝趾，坝踵以及下游坝面折坡处5个结点作为变形观测点。

在算例分析中，取反演参数为坝基岩体的变形模量，依据工程经验，反演参数取值范围为1.0～30.0 GPa。

除反演参数外，模型介质的其他物理力学参数如下:坝体混凝土密度ρ1=2400 kg/m3，弹性模量E=20 GPa，泊松比v1=0.167;坝基岩体密度ρ2=2 000 kg/m3，泊松比v2=0.25，摩擦系数f=1.05，黏聚力c=0.95 MPa。计算中坝体混凝土采用线弹性本构模型，坝基岩体采用基于Drucker-Prager屈服准则的理想弹塑性本构模型。计算以坝基岩体的自重应力场作为初始地应力场，作用坝体的荷载包括坝体自重、上下游面水压力以及扬压力。

首先给定坝基岩体变形模量(取为9 GPa)进行有限元计算，并以5个测点处有限元计算所得的位移值(见表1)作为反演所需的实测变形数据，随后应用PSO-ABAQUS联合反演程序反演坝基岩体力学参数(变形模量)，最后将反演所得的变形模量以及相应的变形场与给定的变形模量及相应的变形场进行对比分析，以验证本文所提方法以及程序开发的正确性及有效性。

图2 重力坝有限元模型及测点位置Fig.2 FEM mesh of gravity dam and location of measuring points

利用PSO-ABAQUS联合反演程序，对算例开展了坝基岩体力学参数反演分析。反演中取粒子群组数为5组，目标函数预定最小阈值为0.05。反演所得的坝基岩体弹性模量为8.797 GPa，误差为2.3%。

图3为在给定力学参数条件下、对坝基岩体赋予反演参数下的坝体水平向、垂向位移分布云图。由图3可知，给定参数和反演参数下模型计算位移场基本一致。由表1可知，5个测点的实测位移值与基于反演参数的计算位移值亦非常接近。

表1 各测点位移Table 1 Displacement of measuring points mm

图3 坝体水平向和竖向位移云图(单位:mm)Fig.3 Contour of horizontal and vertical displacement of dam(units:mm)

图4为了优化反演中目标函数的变化过程。由图4可知，在较少粒子组数和较小阈值条件下，反演经过27次迭代就达到了较高的精度，可以预计，若设定较多的粒子组数并采用较大的阈值，优化迭代的次数还可以进一步减少，说明本文所提出的PSO-ABAQUS联合反演法具有较高的效率。

图4 目标函数值变化过程线Fig.4 Change process of object function value

5 结 语

合理确定坝基岩体力学参数是开展坝体-坝基系统的应力变形分析及稳定性评价并取得合理成果的关键之一，但基于通常的试验和工程类比所确定的力学参数往往与实际情况不符。鉴于此，本文将PSO算法引入坝基岩体力学参数反演领域，并提出基于PSO算法和ABAQUS的坝基岩体力学参数联合反演法。在介绍粒子群优化算法基本理论的基础上，构建了坝基岩体力学参数的数学反演模型，给出了具体的实施流程并开发了相应的程序，实现了基于施工和运行期实测变形资料的坝基岩体力学参数PSO-ABAQUS联合反演。算例分析表明，本文所提的PSO-ABAQUS联合反演法不仅简便易行，而且效率较高，是一种用于合理确定坝基岩体力学参数的通用方法。

［1］贺里尧.一般性坝基岩体力学参数取值研究路线的探讨［D］.兰州:兰州大学，2009.

［2］张强勇，向文，杨文东，等.坝区岩体蠕变参数反演与边坡开挖流变计算分析［J］.武汉大学学报:工学版，2008，41(5):72-76.(ZHANG Qiangyong，XIANG Wen，YANG Wendong，et al.Creep parameters inversion for dam zone rockmass and rheological computational analysis of slope excavation［J］.Engineering Journal of Wuhan University，2008，41(5):72-76.(in Chinese))

［3］常晓林，喻胜春，马刚，等.基于粒子迁徙的粒群优化算法及其在岩土工程中的应用［J］.岩土力学，2011，32(4):1077-1082(CHANG Xiaolin，YU Shengchun，MA Gang，et al.Particle swarm optimization based on particle migration and its application to geotechnical engineering［J］.RocKand Soil Mechanics，2011，32(4):1077-1082.(in Chinese))

［4］张强勇，陈芳，杨文东，等.大岗山坝区岩体现场剪切蠕变试验及参数反演［J］.岩土力学，2011，32(9):2584-2590.(ZHANG Qiangyong，CHEN Fang，YANG Wendong，et al.Field shear creep test and creep parameters inversion for dam zone rocKmass of Dagangshan hydropower station［J］.RocKand Soil Mechanics，2011，32(9):2584-2590.(in Chinese))

［5］陈益峰，周创兵.隔河岩坝基岩体在运行期的弹塑性力学参数反演［J］.岩石力学与工程学报，2002，21(7):968-975.(CHEN Yifeng，ZHOU Chuangbing.BacKanalysis on elastic-plastic mechanic parameters of rocKfoundation of Geheyan dam during running period［J］.Chinese Journal of RocKMechanics and Engineering，2002，21(7):968-975.(in Chinese))

［6］倪绍虎，肖明，何世海，等.地下工程并行优化反演分析及算例验证［J］.岩石力学与工程学报，2013，32(3):501-511.(NI Shaohu，XIAO Ming，HE Shihai，et al.BacKanalysis in underground engineering based on parallel computing and optimization algorithm and its verification［J］.Chinese Journal of RocKMechanics and Engineering，2013，32(3):501-511.(in Chinese))

［7］李金风，杨启贵，徐卫亚.基于改进粒子群算法CHPSO-DS的面板坝堆石体力学参数反演［J］.岩石力学与工程学报，2008，27(6):1229-1235.(LI Jinfeng，YANG Qigui，XU Weiya.BacKanalysis mechanical parameters of rockfill based on modified particle swarm optimization CHPSO-DS［J］.Chinese Journal of RocKMechanics and Engineering，2008，27(6):1229-1235.(in Chinese))

［8］苏国韶，张克实，吕海波.位移反分析的粒子群优化-高斯过程协同优化方法［J］.岩土力学，2011，32(2):510-515.(SU Guoshao，ZHANG Keshi，LYU Haibo.A cooperative optimization based on particle swarm optimization and Gaussian process for displacement bacKanalysis［J］.RocKand Soil Mechanics，2011，32(2):510-515.(in Chinese))

［9］罗润林，阮怀宁，黄亚哲，等.岩体初始应力场的粒子群优化反演及在FLAC3D中的实现［J］.长江科学院学报，2008，25(4):73-76.(LUO Runlin，RUAN Huaining，HUANG Yazhe，et al.Particle swarm optimization inversion method of initial ground stress and implementation in FLAC3D［J］.Journal of Yangtze River Scientific Research Institute，2008，25(4):73-76.(in Chinese))

［10］张鹄志，郭建青.粒子群优化算法在确定越流含水层参数中的应用［J］.水利水电科技进展，2011，31(3):13-16.(ZHANG Huzhi，GUO Jianqing.Application of particle swarm optimization algorithm to determination of leakage aquifer parameters［J］.Advances in Science and Technology of Water Resource，2011，31(3):13-16.(in Chinese))

［11］李占超，侯会静.基于改进粒子群优化算法的施工期拱坝结构性态反演分析［J］.水利水电科技进展，2011，31(4):24-28.(LI Zhanchao，HOU huijing.Inverse analysis of structural behaviors of arch dams during construction period based on improved particle swarm optimization［J］.Advances in Science and Technology of Water Resource，2011，31(4):24-28.(in Chinese))

［12］赵迪，张宗亮，陈建生.粒子群算法和ADINA在土石坝参数反演中的联合应用［J］.水利水电科技进展，2012，32(3):43-47.(ZHAO Di，ZHANG Zongliang，CHEN Jiansheng.A combined application of particle swarm optimization algorithm and ADINA for parametric inversion of earth rocKdam［J］.Advances in Science and Technology of Water Resources，2012，32(3):43-47.(in Chinese))

［13］张丽平.粒子群优化算法的理论及实践［D］.杭州:浙江大学，2005.

［14］贾善坡，伍国军，陈卫忠.基于粒子群算法与混合罚函数法的有限元优化反演模型及应用［J］.岩土力学，2011，32(增刊2):598-603.(JIA Shanpo，WUGuojun，CHENWeizhong.Application of finite element inverse model based on improved particle swarm optimization and mixed penalty function［J］.RocKand Soil Mechanics，2011，32(Sup2):598-603.(in Chinese))

［15］徐磊.基于ABAQUS的强度储备安全系数精确自动求解［J］.三峡大学学报:自然科学版，2011，33(3):10-13.(XU Lei.Accurate auto-calculation of strength reserve safety coefficients based on ABAQUS［J］.Journal of China Three Gorges University:Natural Sciences，2011，33(3):10-13.(in Chinese))