多孔材料弹性模量预测的数值方法

顾 政，郑建军，周欣竹

（浙江工业大学建筑工程学院，杭州 310014）

多孔材料普遍存在于自然界中，木材、生物的骨骼以及岩石等都是天然的多孔材料。随着科学技术的发展，出现了越来越多用金属、陶瓷和高聚合物等制成的人造多孔材料［1］。这些多孔材料已广泛应用于各个工程领域，它们不仅具有多种优异的性能，而且制造工艺简单。因此，研究其力学性能具有突出的重要性。

由于多孔材料是由孔隙和固相所组成的复合体，孔结构（如孔形状、孔隙率和孔的连通性等）是影响宏观弹性性能的主要因素，因而细观结构与宏观力学性能之间的定量关系成为当前国际工程界的前沿课题之一。Voigt和Reuss分别根据等应变和等应力假设给出了多晶体材料体积模量和剪切模量的近似解［2］，Gibson和Ashby［3］在单孔单元的基础上建立模型，获得了蜂窝多孔材料二维弹性参数，即Gibson－Ashby方程，Roberts［4］研究了开孔和闭孔泡沫的弹性性能。随着数值方法和计算机技术的日益发展，有限元法被广泛用于多孔材料的力学性能分析［5］，对“代表性体积元”进行数值求解，获得宏观力学性能。但对于复杂的多孔材料，不仅网格划分极其困难，总刚度矩阵占据大量内存，而且总刚度方程求解花费大量时间，以至于无法获得满意的数值解。为此，该文在前人工作的基础上，应用快速傅里叶变换法讨论了多孔材料弹性模量的计算方法。

1 数值方法

1.1 多孔材料模拟

类似于“代表性体积元”，可以从细观结构图像的像素点上获得结构单元的代表性信息［6］。因而为了能较准确地预测多孔材料的弹性模量，首先应建立多孔材料模型，作为初步尝试，文章仅考虑二维模型。多孔材料区别于普通密实固体材料的最显著特点是具有孔隙，多孔材料建模时应着重考虑孔隙分布特点以及孔隙率大小。大量的试验研究表明［7］，多孔材料中的孔隙率、孔径分布、孔隙位置等均服从一定的统计分布规律，如随机分布和正态分布等。因此，建立多孔材料几何模型的关键是按照一定的概率分布确定孔隙大小和位置，在数学上可以通过各种变换或抽样来实现。

为了便于计算，该文假设孔隙为圆形，而且大小相等、互不重叠。在模拟孔隙时，先选取一边长为L的正方形，在分布第i个半径为R的圆孔时，在正方形区域内生成其圆心坐标（xi，yi），如果第i个圆孔与前面已经分布某一个或几个圆孔重叠，则重新生成第i个圆孔的圆心坐标；如果第i个圆孔不与前面已经分布的（i－1）个圆孔重叠，那么继续分布第i＋1个圆孔，直到达到给定的孔隙率为止。作为一个算例，设L＝100mm，R＝4mm，孔隙率C分别为0.1、0.3和0.5，所获得的孔分布如图1所示。

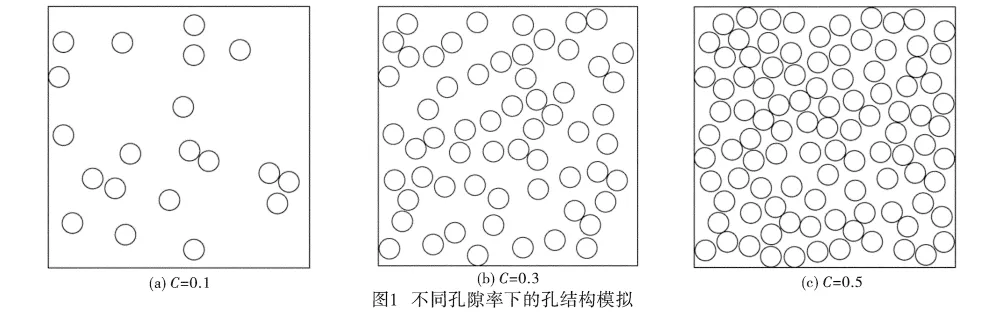
1.2 基本方程

首先在模拟区域内等距离选取像素点，根据快速傅里叶变换原理，每个二维细观结构分布图都包含2K×2K个像素点，这些像素点各自具有力学性质，且相互独立，计算步骤如下：

1）将图像划分为2K×2K个细胞单元，如图2所示，取每个细胞单元的中心点为像素点，这里称K为像素点个数指数。

2）对每个像素点进行判断，如果落在孔隙内，弹性模量取为零；如果落在固相内，弹性模量取单位值，这样所获得的多孔材料的弹性模量为相对值。

多孔材料各点的弹性张量Cijkl（x）是坐标x的函数，其应力－应变关系可表示成

式中，C0ijkl为弹性张量常数，τij（x）定义为

通过引入周期性格林张量Γijkl，式（1）的解可表示为［6］

对式（3）进行傅里叶变换有

对于各向同性材料，（ξ）为［6］

式中，λ和μ为拉梅常数，εi为傅里叶空间坐标。

1.3 迭代求解

方程（1）～方程（4）可以通过以下迭代方法进行求解：

1）给定初始均匀应变ε0ij，由式（1）求得初值应力σ0ij；

2）对于第i＋1次迭代，先由（2）计算τij（x），对τij（x）进行傅里叶变换求得＾τij（ξ），再检验收敛性；

3）由式（4）计算第i＋1次迭代应变，再将应变进行傅里叶反变换；

4）由式（1）计算应力。

一旦迭代收敛，计算各点的加权应力和加权应变，最后获得多孔材料的弹性模量。该文以前后两次迭代值的相对误差小于10－3作为收敛准则。

2 收敛性和有效性验证

2.1 收敛性验证

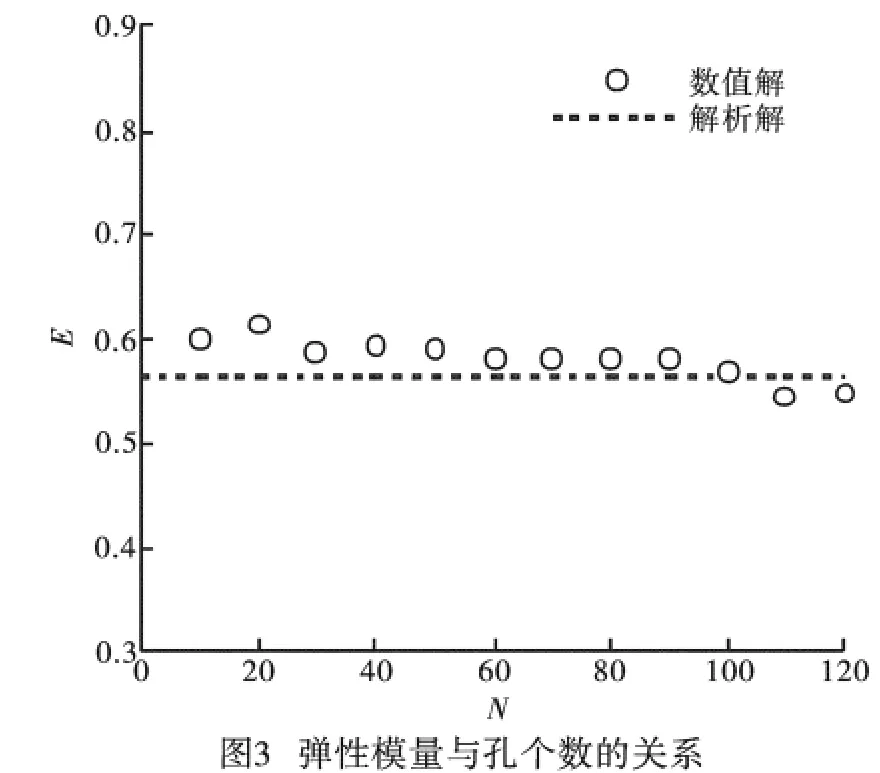
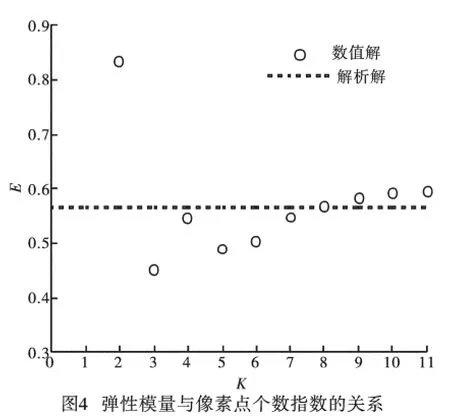
在下面的计算中，取正方形边长为1 000mm，孔隙率C＝0.2，像素点个数为28×28个，固相材料的泊松比为0.3，计算所得的相对弹性模量与孔隙个数之间的关系如图3所示，其中，虚线表示解析解［8］。从该图可以看出，当孔隙个数较少时，弹性模量上下波动，当孔隙数大于100时，弹性模量基本趋于稳定，这与文献［9］的结论一致，这是因为孔隙越多，材料越均匀，像素点所代表的结构单元性质越接近于真实情况。再取孔隙个数为100，相对弹性模量与像素点个数指数之间的关系如图4所示。从该图可以看出，当K较小时，弹性模量上下波动幅度较大，随着K的增大，结果趋于稳定，K＝10与K＝11之间弹性模量的相对误差仅为0.3%，表明该方法已经收敛。图4还表示，随着像素点的增加，数值解与解析解越接近，这是因为随着像素点的增加，结构单元性质得到更细致的描述，更接近于真实情况，另一方面，由于傅里叶变换本身具有一定的误差，当像素点超过一定值后，累积误差也会影响计算结果。由图4还可以得出，当像素点个数为256×256时，数值解与解析解最接近。

2.2 有效性性验证

基于前面的讨论，取孔隙个数为100，像素点个数为256×256，相对弹性模量随孔隙率变化如图5所示。从图5可以看出，数值解与解析解良好吻合，当孔隙率为0.10、0.20、0.30、0.40和0.50时，两者之间的误差分别为6.70%、1.17%、2.12%、3.36%和7.03%，其平均值为4.37%。因此，文中方法的有效性得到初步证实。

3 结 论

a.基于Moulinec和Suquet所提出的快速傅里叶变换法，讨论了多孔材料弹性模量计算，通过与文献中的解析解比较，初步证实了该数值方法的有效性。

b.定量评价了孔隙个数和像素点个数对计算结果的影响，发现多孔材料越均匀、像素点个数越多，数值解越精确。

［1］ 刘培生.多孔材料引论［M］.北京：清华大学出版社，2004.

［2］ Torquato S.Random Heterogenerous Materials：Microstructure and Macroscopic Properties［M］.New York：Springerverlag，2001.

［3］ Gibson L J，Ashby M F.Cellular Solids：Structure and Properties［M］.Cambridge：Cambridge University Press，1997.

［4］ Roberts A P，Garboczi E J.Elastic moduli of model random three－dimensional closed－cell cellular solids［J］.Acta materialia，2001，49（2）：189－197.

［5］ Bardenhagena S G，Brydona A D，Guilkey J E.Insight into the physics of foam densification via numerical simulation［J］.Journal of the Mechanics and Physics of Solids，2005，53（3）：597－617.

［6］ Moulinec H，Suquet P.A Numerical Method for Computing the Overall Response of Nonlinear Composites with Complex Microstructure［J］.Computer Methods in Applied Mechanics and Engineering，1998，157（1－2）：69－94.

［7］ 鞠 杨，杨永明，宋振铎，等.岩石孔隙结构的统计模型［J］.中国科学E辑，2008，38（7）：1026－1041.

［8］ Zheng Q S，Hwang K C.Two－dimensional Elastic Compliances of Materials with Holes and Microcracks［J］.Proceedings of the Royal Society of London，1997，453（1957）：353－364.

［9］ Hu N，Wang B，Tan G W，et al.Effective Elastic Properties of 2－D Solids with Circular Holes：Numerical Simulations［J］.Composites Science and Technology，2000，60（9）：1811－1823.