基于网格覆盖法的城市巡逻车问题的设置与求解
2013-04-13王小朋牛剑敏
王小朋 牛剑敏 刘 建
(1.武汉理工大学 理学院数学系,湖北 武汉 430070;2.长治市郊区职业高中,山西 长治 046000;3.吕梁学院 汾阳师范分校,山西 汾阳 032200)
随着国民经济的快速发展与城市化进程的速度加快,警车在城市道路上的巡逻所起的作用越来越大,它既能减少一定的违法犯罪行为,又能大大增加市民出行的安全感,同时合理的设置和制定巡逻方案将会在很大程度上缩短接警处理突发事件的时间.因此,合理的运用警车和设置制定巡逻方案将会使警车的巡逻效率达到最优.长治市是十大魅力城市之一,下文将以其为例,为该市城区警车的设置制定巡逻方案及求解模型与方法.
为了便于问题的解决,现将该市城区地形图 (该图的比例尺:1:83334),下图1进行相应的假设与处理,即:把图1中的道路交叉口看成图论中所说的结点并且给其命名,相邻两个路口间的道路看成是图论中的边.则得到下图2.从图2可知该区域的交叉路口(结点)数和各个结点的坐标,运用Matlab编程可得到任意相邻两个交叉路口距离分别为:
AB=1964.61,AI=1037.40,BC=808.95,BE=819.19,CD=1430.28,CF=818.41,DH=464.41,EF=783.85,EK=338.17,FG=813.94,FL=407.06,GM=402.92,GH=787.46,HN=785.88,LJ=874.93,LO=495.84,JP=469.06,JK=829.96,KQ=449.07,KL=740.91,LR=349.28,LM=823.77,MS=366.74,MN=747.33,OX=908.61,OP=1038.70,PY=1024.89,PQ=802.31,QT=596.41,QR=773.18,RU=836.30,RS=806.04,SV=867.44,NW=1135.30,TU=810.25,YZ=1380.51,UZ=457.93,VW=929.14,XZ3=651.23,Z3Z4=1298.08,YZ4=645.37,Z4Z5=1278.83,ZZ1=827.65,Z1Z2=960.47,ZZ5=353.84,VZ1=392.17,WZ2=494.77
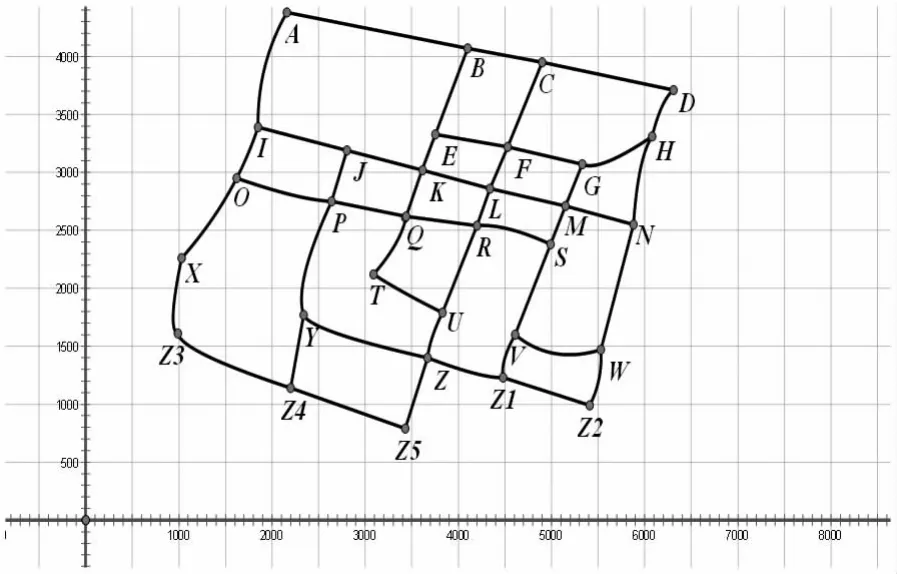
图2
1 区域内最少警车数量分析
以长治市为例,该市增加了一批配备有GPS卫星定位系统及先进通讯设备的110警车.设110警车的平均巡逻速度为40km/h,接警后的平均行驶速度为60km/h,警车接警后三分钟到达案发现场.如何设置警车才能保证在整个城区区域内巡逻所需警车数量最少,并且警车巡逻范围所覆盖的交叉路口超过90%.考虑到实际情况中,单辆警车的巡逻只是在小区域内进行的而不可能在短时间内巡逻整个城市,故可将整个城市的区域划分成多个小区域,每个小区域派一辆警车循环巡逻.因此,要考虑该如何划分整个城区区域.从整个城区区域地形图上可以看到,该区域的交叉路口大多数为十字路口、丁字路口及V字路口.假设警车所巡逻的范围是一定的,先固定警车的初始位置.将一辆警车想象成一个点,搜索到与这个点距离小于警车接警后所走的最大距离的所有点,可构成一个小区域.即以该点为中心小于最大距离长为半径的圆形区域.假设在各个路口处都设置上警车来巡逻,任意两个相邻交叉路口间的距离若不是该圆域直径的整数倍,那么在道路上也得设置警车巡逻.这样一来他们巡逻的范围难免会存在交集,交集部分越大,所需的警车数量就越多.因此,得到的解是一个可行解而不是最优解.因此还需应用网格覆盖法来做进一步的处理,应用网格来覆盖整个区域,需满足方形网格所覆盖的道路上任意两点之间的距离均小于警车接警后三分钟所走的最大距离,且每个方格由一辆警车巡逻.即方形网格所覆盖的道路上,任意一点处均可作为警车的初始位置.这样才能更好的求解出巡逻整个区域所需警车的最少数量.
2 静态警车设置问题的模型
由于警车接警后的平均行驶速度为60km/h,且三分钟内到达案发现场.那么该案发现场距这辆警车的最大距离为(3/60).60=3km.因此,静态的警车设置问题可以归纳为一个最优模型.设警车的数量为n,警车的初始位置是随机分布的.警车所在的巡逻区域为方形区域,各个区域所覆盖的面积与整个城区区域所覆盖的面积进行比较.运用图形覆盖的知识可知,只有方形区域所覆盖的面积大于整个城区区域所覆盖的面积才能把整个城区区域给覆盖,而且还要满足已知条件中所强调的警车巡逻所覆盖的交叉路口应达到90%.假设m(i)(1≤i≤n)表示第i辆警车巡逻所在的方形区域的面积,MP表示所有警车巡逻所在方形区域的面积和,M表示整个城区所有覆盖的面积和,NP表示警车巡逻所覆盖的结点数,N表示城区地形图中的结点总数,RP表示警车巡逻所覆盖的结点率.则以上的最优模型为:
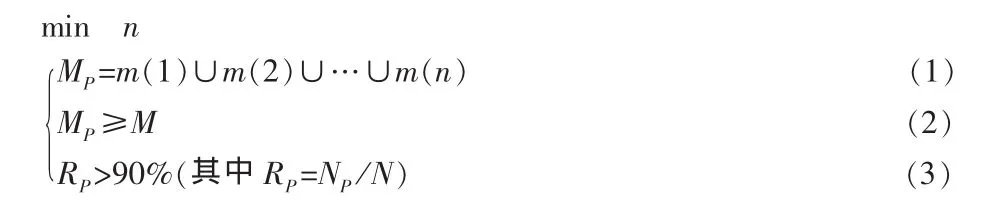
3 区域内最少警车的计算
由于警车的初始位置是随机分布的且假设警车的初始位置是静止状态的.由于警车接警后的的平均行驶速度为60km/h,则接警后三分钟所能行驶的最大距离为3000m.运用网格来覆盖整个城区区域,相当于用方形纸片来覆盖一个不规则图形.假设每个小方形区域的周长为3000m,即警车接警后巡逻这个方形区域所需时间在3分钟之内.故只需说明周长为3000m的方形所覆盖的城区区域,警车接警后到达案发现场的时间均在3分钟之内.通过对网格所覆盖的城区区域做进一步的定性分析可知:除孤立结点外,任意两个可达结点间的距离小于正方形的周长都可以作为警车的初始位置.故对长治市城区地形图进行方形网格覆盖.用两簇平行线构造出方形网格,且每个网格由一辆警车进行巡逻.由于每个网格的周长为3000m.则其对角线长为1057.5m.而经过数学处理的图2是在城区地形图1的整体上缩小了1.68倍得到的.故在进行网格覆盖时,每个网格的图上周长为1785.71m,对角线长为631.35m.为了方便计算,选取的两簇平行线方程为:
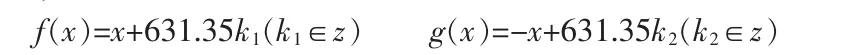
即得到下图3,再根据之前分析的内容即任意两个可达结点间的距离小于方形的周长都可以作为警车的初始位置也就是被方形网格所覆盖的道路上任意一点处都可作为警车的初始位置,通过优化处理覆盖之后,可以得出巡逻完整个区域最少需要23辆警车.即下图4:
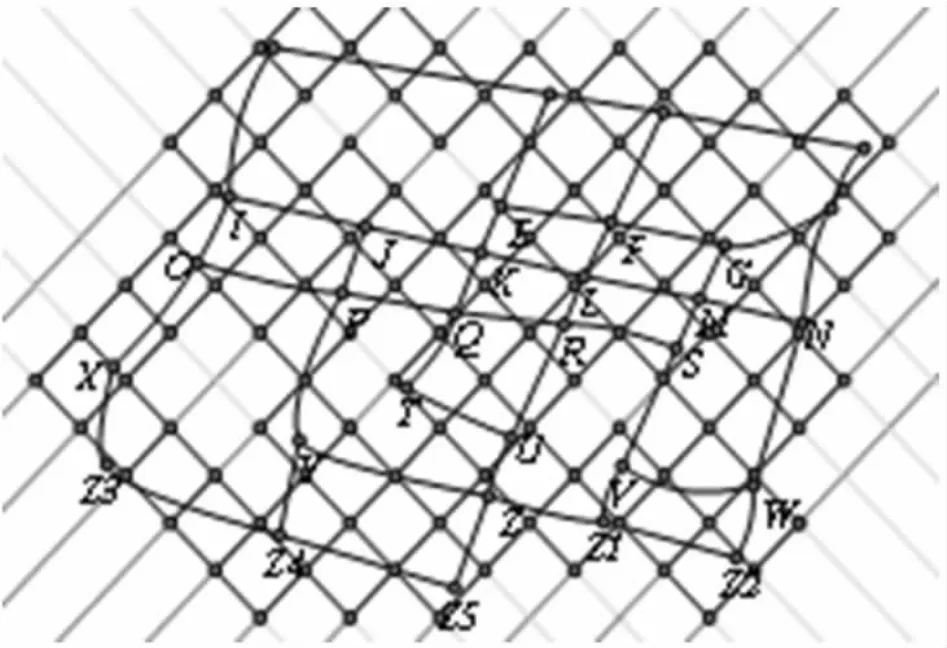
图3
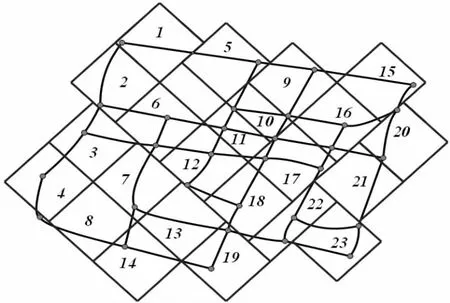
图4
验证约束条件(2),由于每辆警车巡逻所在方形区域的面积为m(i)≈797193.876m2,故可知所有警车巡逻所在方形区域面积和为MP≈17540051m2=17.5km2,而整个城区所覆盖的面积为M≈13km2即满足MP≥M.验证约束条件(3),网格区域所覆盖的结点数为30,而整个城区区域图中共有 31 个交叉路口则 RP=(NP/N).100%≈96.8%>90%即满足约束条件(3),满足原优化问题的约束条件,故23即为原问题的最优解.
[1]张仲斐.110警车配置及巡逻方案[D].浙江:浙江大学.
[2]林阳斌,陈碧黎,苏圳泷.110配置及巡逻方案[J].数学的实践与识.
