基于主成分分析、聚类分析的绿化树种及其生理指标分类

杨 旸

（东南大学 机械工程学院，江苏 南京 211189）

在环境保护、环境治理、城市规划、园林设计、住宅绿地设计中,可供选择的绿化树种种类繁多，生理指标也较为复杂，但各生理指标具有一定的相关性，各不同树种也具有一定的功能类别特性.在参考了大量论文及书籍后，本文应用主成分分析和聚类分析的方法对绿化树种的生理指标和不同种类的树种进行分类，以期为环保部门和城市建设提供新的思路.在相关领域，主成分分析法被用于小兴安岭低质林不同皆伐改造模式评价[9]、居民自愿供给城市森林生态服务研究[5]，均有明显的效果，将绿化树种及其生理指标运用主成分分析法和聚类分析法，可以将各个生理指标归纳为相似相近的类别、将各个树种同样划分类别，大大简化了实际操作中树种选择的难度，有效增强了对周围环境的针对性，也行有效减少树种选择失误造成的经济损失.

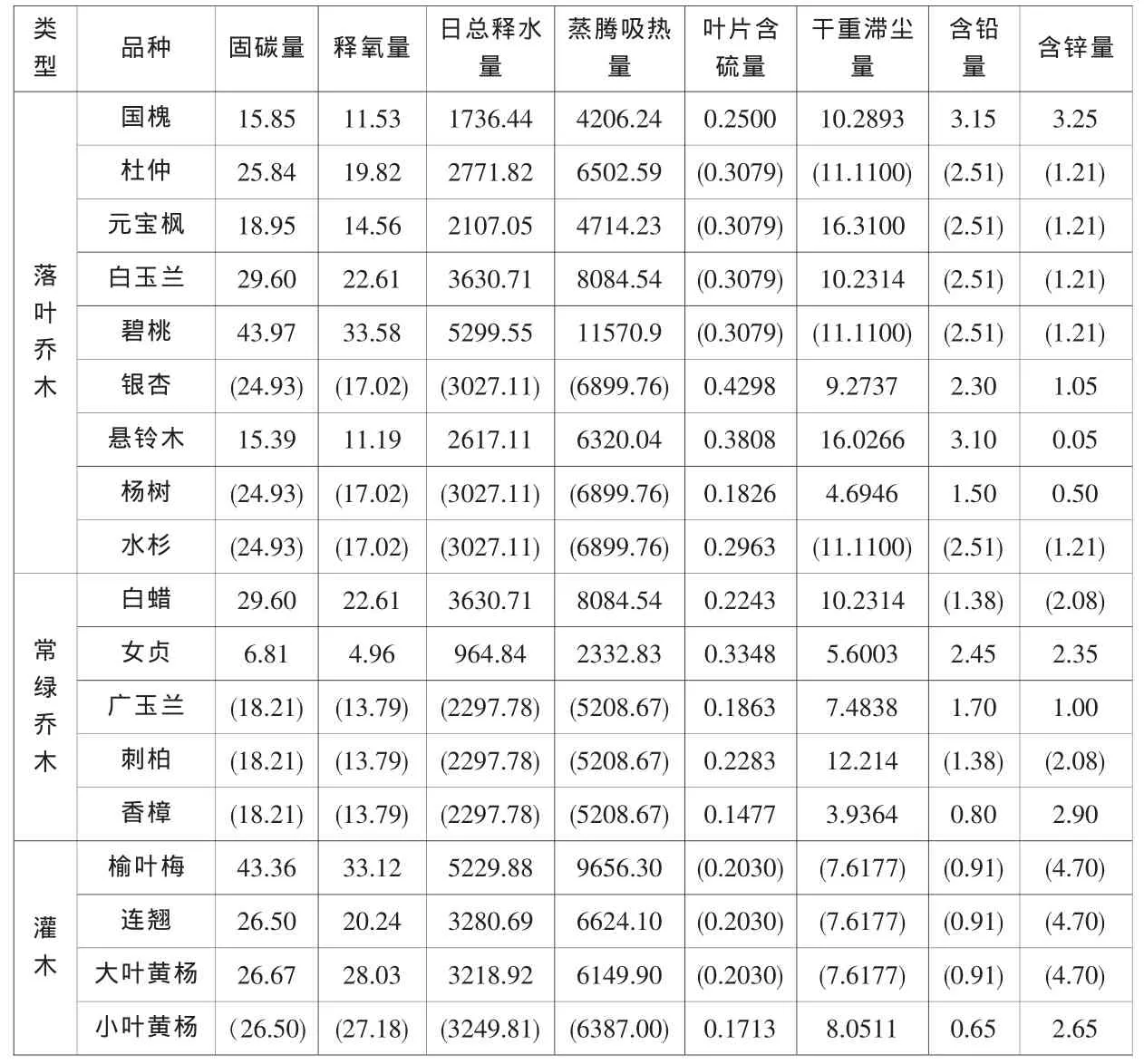
表1 绿化植物各项生理指标原始数据表

1 数据来源

本文所有的数据都收集引用自参考论文.参考论文中的数据经过统计并不能涵盖每个树种的每个生理指标，只取了其中较为有代表性的树种，对于缺少的项目，取参考文献中所有同类树种（同为落叶乔木、常绿乔木或者为灌木）单项指标求平均值，同时也能降低其对整个数据分析的影响.各树种的各项生理指标原始数据表1.表中只列出了常规的特征性指标，而一些较少的指标，对于分析研究没有很大影响，便没有在表中列出.已取得的平均值在表中已用括号做出了标记.

2 主成分分析法和聚类分析法（Principal Component Analysis， PCA；Cluster Analysis，CA）

主成分分析法也称主分量分析或矩阵数据分析，通过变量变换的方法把相关的变量变为若干不相关的综合指标变量.

若某研究对象有两项指标 ζ1和 ζ2，从总体 ζ(ζ1，ζ2)中抽取了N个样品，它们散布在椭圆平面内(见图 1)，指标 ζ1与 ζ2有相关性.η1和 η2分别是椭圆的长轴和短轴，η1⊥η2， 故 η1与 η2互不相关.其中 η1是点 ζ(ζ1，ζ2)在长轴上的投影坐标，η2是该点在短轴上的投影坐标.从图1可以看出点的N个观测值的波动大部分可以归结为η1轴上投影点的波动，而η2轴上投影点的波动较小.若η1作为一个综台指标，则η1可较好地反映出N个观测值的变化情况，η2的作用次要.综合指标η1称为主成分，找出主成分的工作称为主成分分析.

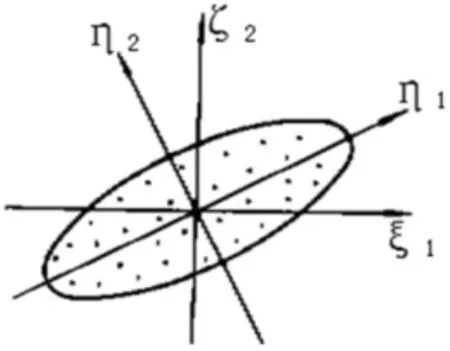
图1 主成分分析法示意图

可见，主成分分析即选择恰当的投影方向，将高维空间的点投影到低维空间上，且使低维空间上的投影尽可能多地保存原空间的信息，就是要使低维空间上投影的方差尽可能地大[6].

给定一个对象集合 X={x1，x2，…，xn}，假设每个对象 xi，i=1，2…，n含有m个特征，在此用向量的方式来表示对象的特征，xi=(l1，l2，…lm)，聚类分析的过程就是根据对象的特征来分析对象之间的相似程度，并根据某种聚类决策准则来获得聚类结果.聚类的结果用C={c1，c2，…，ck}表示，则聚类结果满足以下条件:c1不为空集，i=1，2，…，k；ci∩cj不为空集，i≠j，j=1，2，…，k.模糊聚类的结果没有上面的约束条件，模糊聚类给出的结果只是对象隶属于每个类的程度.通常聚类分析算法一般包含四个部分:1）特征获取与选择；2）计算相似度；3）分组；4）聚类结果展示.

特征获取与选择就是为了获得能够恰当表示对象属性的数据，并且减少数据的冗余度，在本文的前面一章中已经介绍了部分特征获取与选择的知识.计算相似度就是根据对象的特征来计算对象之间的相似程度，在聚类过程中可能一次性的计算所有对象之间的相似度信息，也可能在聚类分析的过程中按需要来计算对象之间的相似度信息，具体的过程要依据所采用的聚类方法而定，分组就是根据对象之间的相似程度来判断对象之间的类别信息，将类似的对象分组到同一个类中，不相似的对象分组到不同的类中.聚类结果展示可以只是简单的输出对象分组信息，也可以用图形化的方式来展示聚类结果，但是目前的研究趋势要求算法能够自动的归纳出每个不同的分组所代表的类信息并抽象出类中对象的共同特性[12].

3 主成分分析法和聚类分析法的应用

本文均利用SPSS软件对所得数据进行分析处理，得到所要的主成分分析结果和聚类分析结果

3.1 主成分分析

3.1.1 原始数据的处理和标准化

根据主成分分析法的要求先对原始数据进行标准化处理，这里运用的是SPSS统计软件进行的主成分分析，软件在分析过程中会自动进行标准化处理，因此在这里不给出原始数据标准化结果.表2是SPPS软件给出的经过标准化后对变量进行分析计算得出的相关性表.

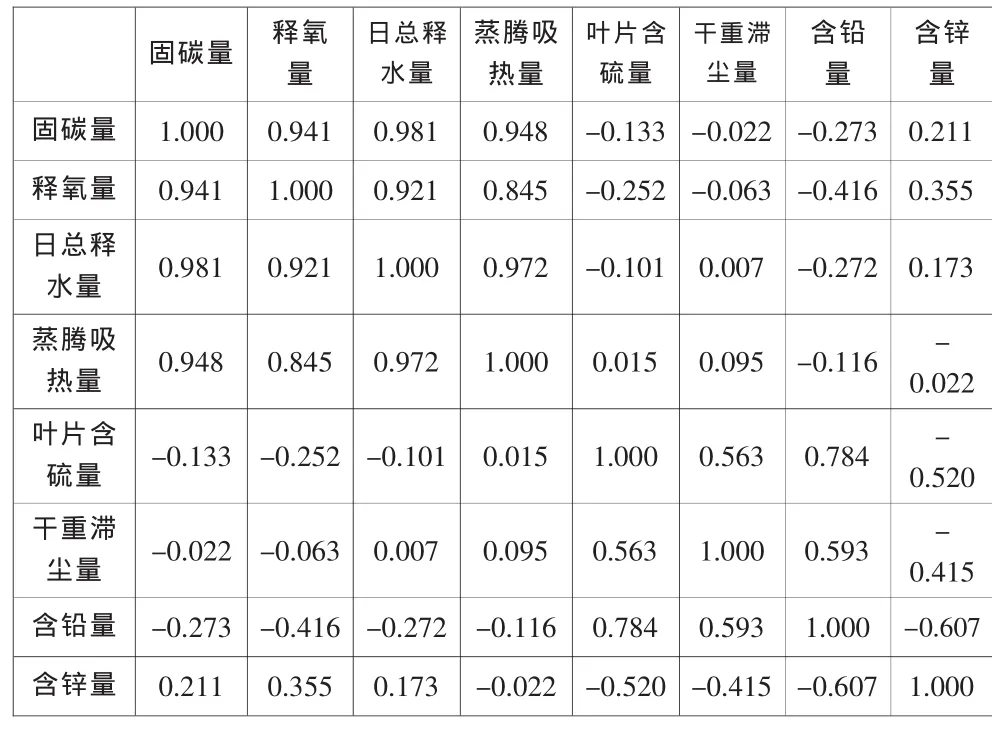
表2 变量相关性表

3.1.2 绿化树种生理指标主成分分析的计算结果

主成分分析的计算结果中，新变量所代表的方差（即对应的特征值）贡献率和由原变量变换为新变量的线性变换系数（即对应的特征向量）就成为我们进行综合分析的重点.在主成分分析中一般要求少数新变量的累积方差贡献率应大于70%[9].下列表3、表4和表5分别给出了原始数据的公因子方差、各个主成分的解释的总方差和主成分的计算结果.图2则是各个主成分的特征值.

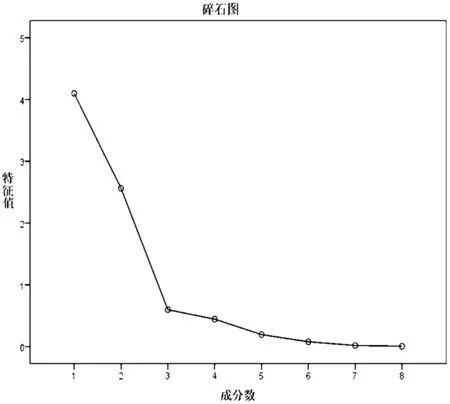
图2 主成分特征值图（碎石图）

图2表明，前三个主成分积累方差贡献率达到90.76%，根据主成分分析法的一般原理，可取前三个具有明显代表性的主成分.原有的8个变量可用三个主成分表示，如表5所示.再进过矩阵的旋转，得到相关性更为明显的三个主成分，如表6，其中相关的变量的相关性都达到了78%以上.

本文可以依据以上计算结果绘出成分图，表明新旧变量之间的关系.同时，也可以为原始的绿化树种生理指标分类再进过旋转矩阵旋转，得到成分图，如图3.

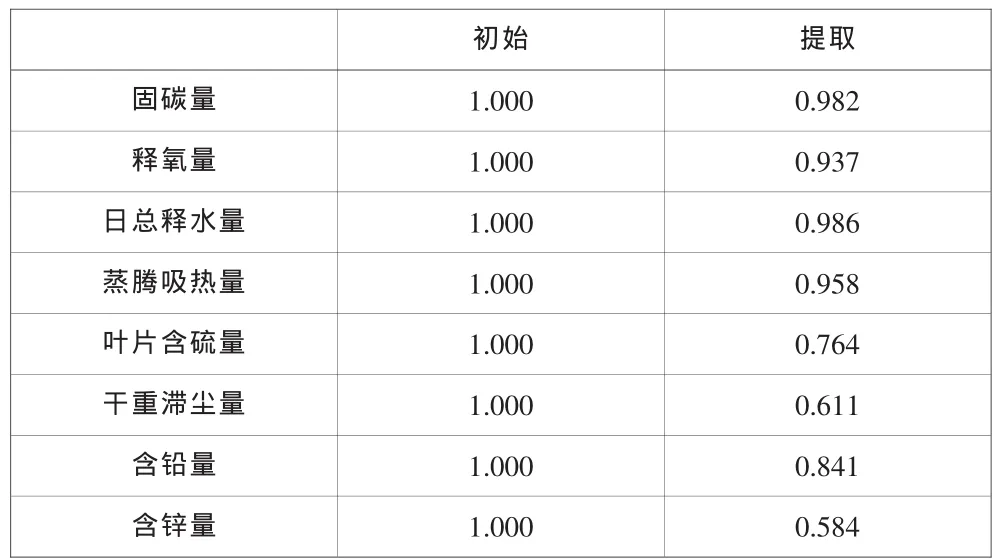
表3 原始数据公因子方差

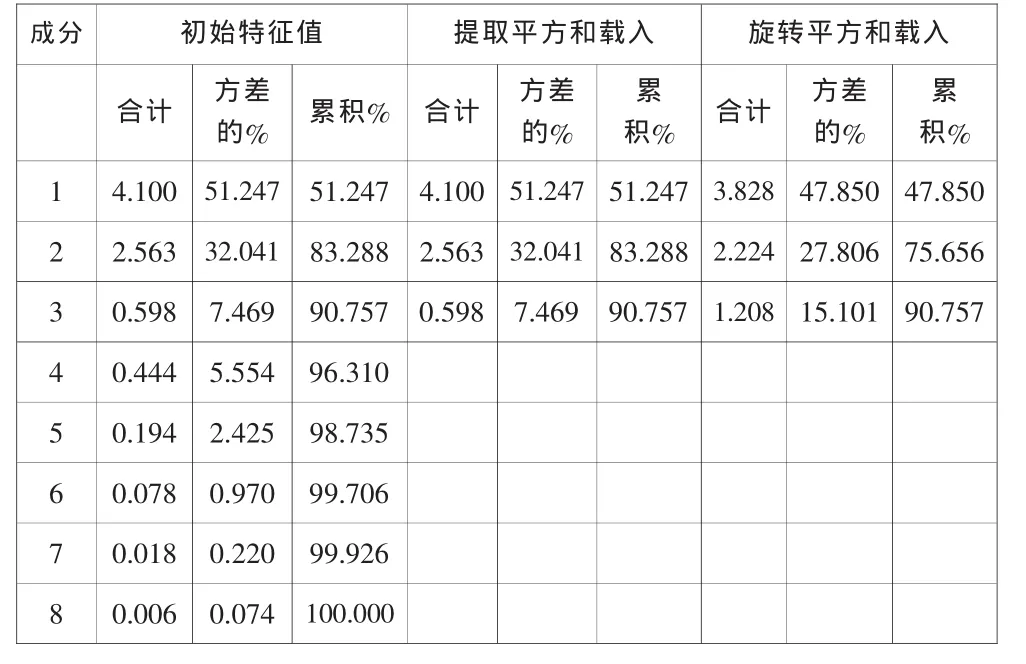
表4 各成分解释的总方差

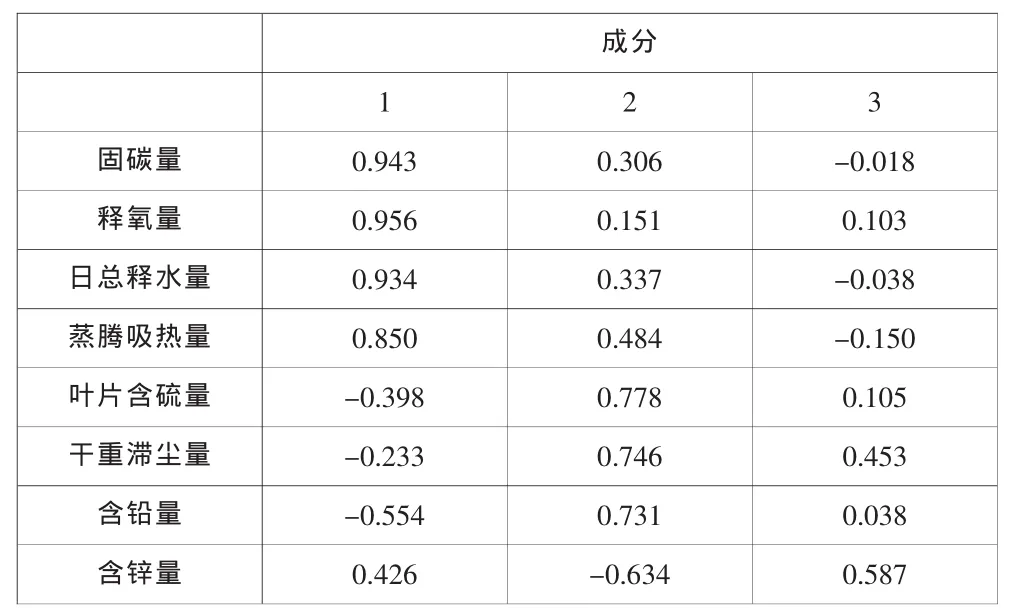
表5 未旋转的成分矩阵

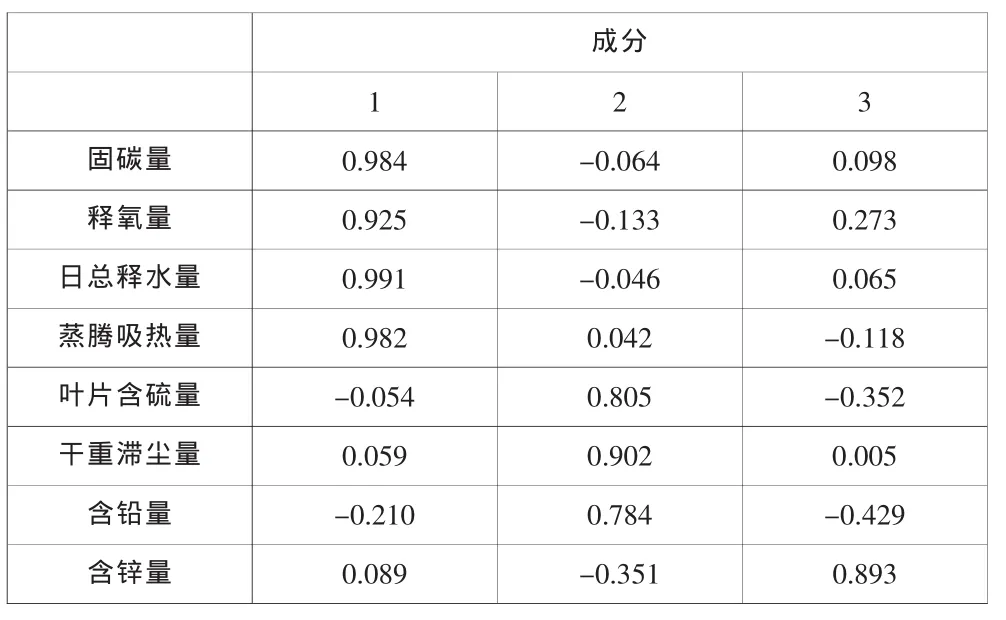
表6 旋转后的成分矩阵

3.1.3 结果分析

由主成分分析的计算结果可以看出，原变量的方差在新变量中的集中度很高，根据绿化树种生理特性指标的实际状况和主成分分析的要求，本文取前3个主成分来反映原来的8个变量，其方差的累计贡献率已达到90.76%，三个主成分的贡献率分别为47.85%,27.81%和15.10%，三个主成分在90.76%的程度上反应了样本的生理特征.可以认为，这三个主成分基本上能够反映出原变量的变化所代表的绿化树种生理特性.

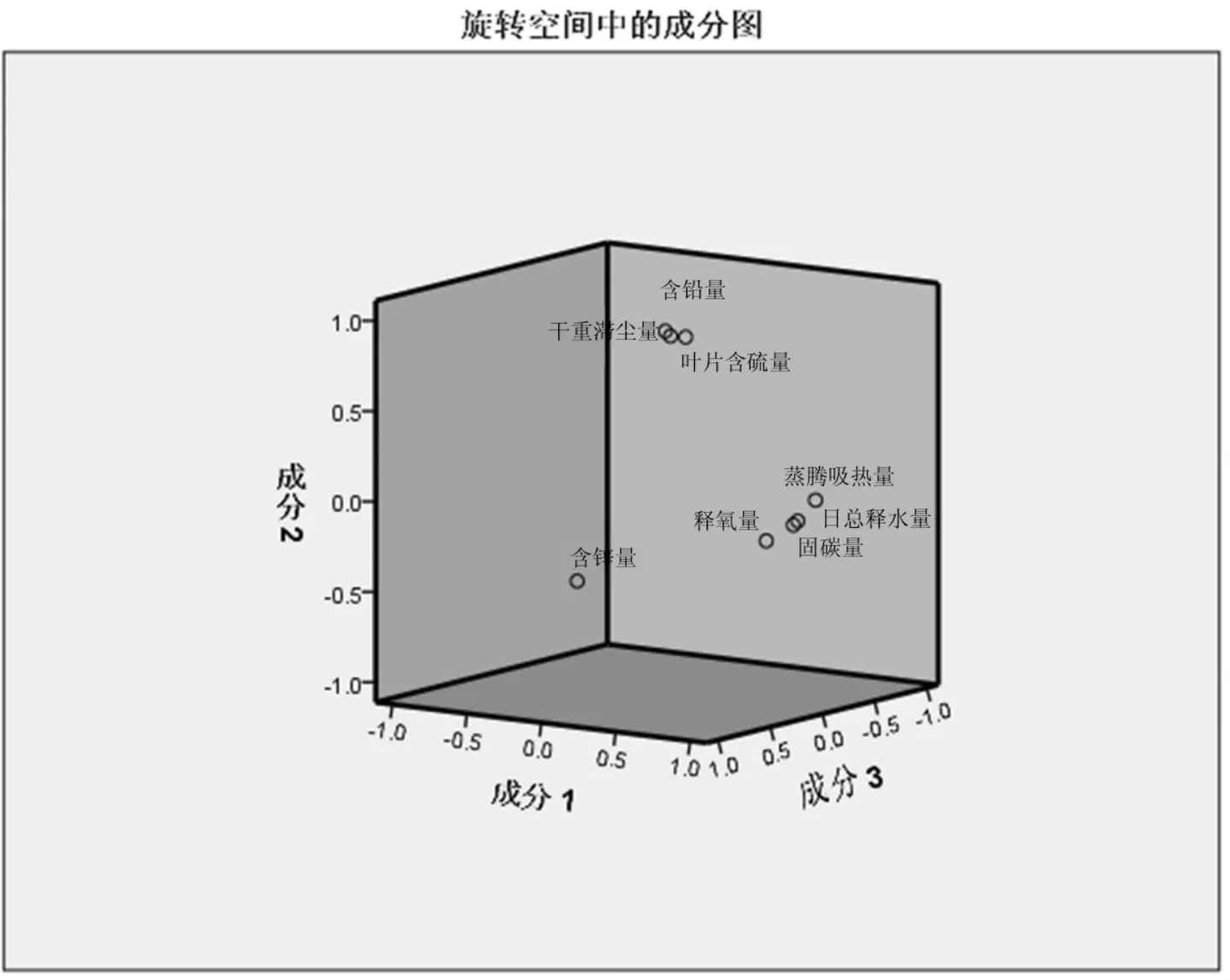
图3 主成分组成成分示意图

在第一主成分中，固碳量、释氧量、日总释水量、蒸腾吸热量四个指数所占权系数较大，并且四个指标变化方向非常一致，呈几乎完全正相关.说明引起这四个指标变化的原因相似，而处理的方式也相关.在植物的生命过程中，光合作用是必不可少的，是植物生存能量的来源,其中固碳量、释氧量、释水量都与光合作用直接相关，蒸腾吸热量因为与释水量有着很直接的关系，因此，蒸腾吸热量与光合作用有着较高程度的间接关系，因此命名该成分为光合作用因子.

在第二主成分中叶片含硫量、含铅量、干重滞尘量三个指数所占权系数较大，并且三个指标变化方向一致，呈正相关.说明三者的原因，处理相近.在植物日常生命过程中，通过叶片上的气孔与外界进行气体交换，而气孔是分布在叶片表面的.而空气中往往因为工业污染、交通尾气污染存在大量粉尘、二氧化硫和重金属铅，在气体交换的过程中，空气中的灰尘、二氧化硫、少量的铅会滞留在叶片表面或者被吸入叶片内部，因此，这三项指数都与气体交换有着很直接的关系，因此明明该成分为气体交换吸收因子.

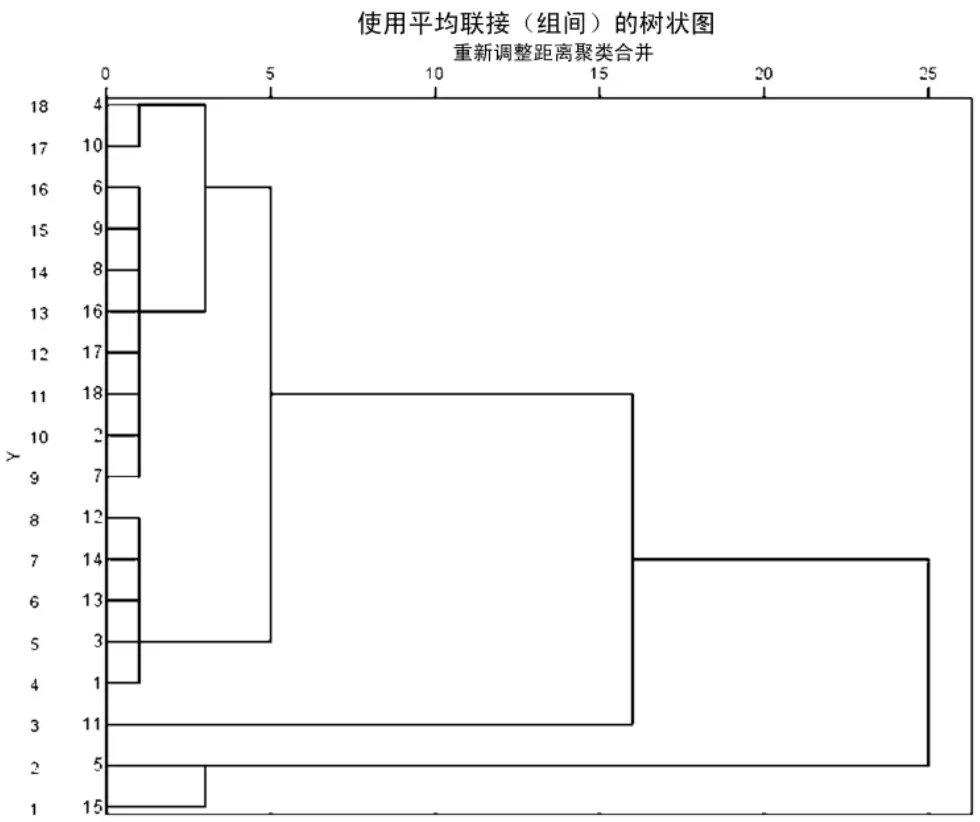
图4 组间连接树状图

在第三主成分中，只有含锌量一个指标，并且贡献度远大于其他指标.锌是植物所需的微量元素，吸收原理与第二个成分不同，虽然锌能够从叶表吸收，但是，由于第二成分根据分析可知其为气体交换因此，因而排除气体交换成分，推断其应为根系吸收成分，即绿化树种对于锌的吸收有别于上文中的第二因子，靠根系的吸收，因此命名为根系微量元素吸收因子.

3.2 聚类分析

3.2.1 原始数据处理

本文采用组间连接法利用SPSS软件对绿化树种的进行分类，表7是得到的组间连接法的平均连接表.

3.2.2 处理所得结果

将表中数据进行进一步处理可得树状图，如图4所示.

3.2.3 结果分析

比对原始数据表，可知总共18中绿化树种，可分为三大类:碧桃、榆叶梅是一类，女贞是单独一类，余下所有树种共为一类；三大类中的第三大类又可分为两类:白玉兰、白蜡、银杏、水杉、杨树、连翘、大叶黄杨、小叶黄杨、杜仲、悬铃木是一类，广玉兰、刺柏、香樟、元宝枫、国槐是一类；该两类中第一类又可分为两类:白玉兰、白蜡和剩下的树种.

4 结论

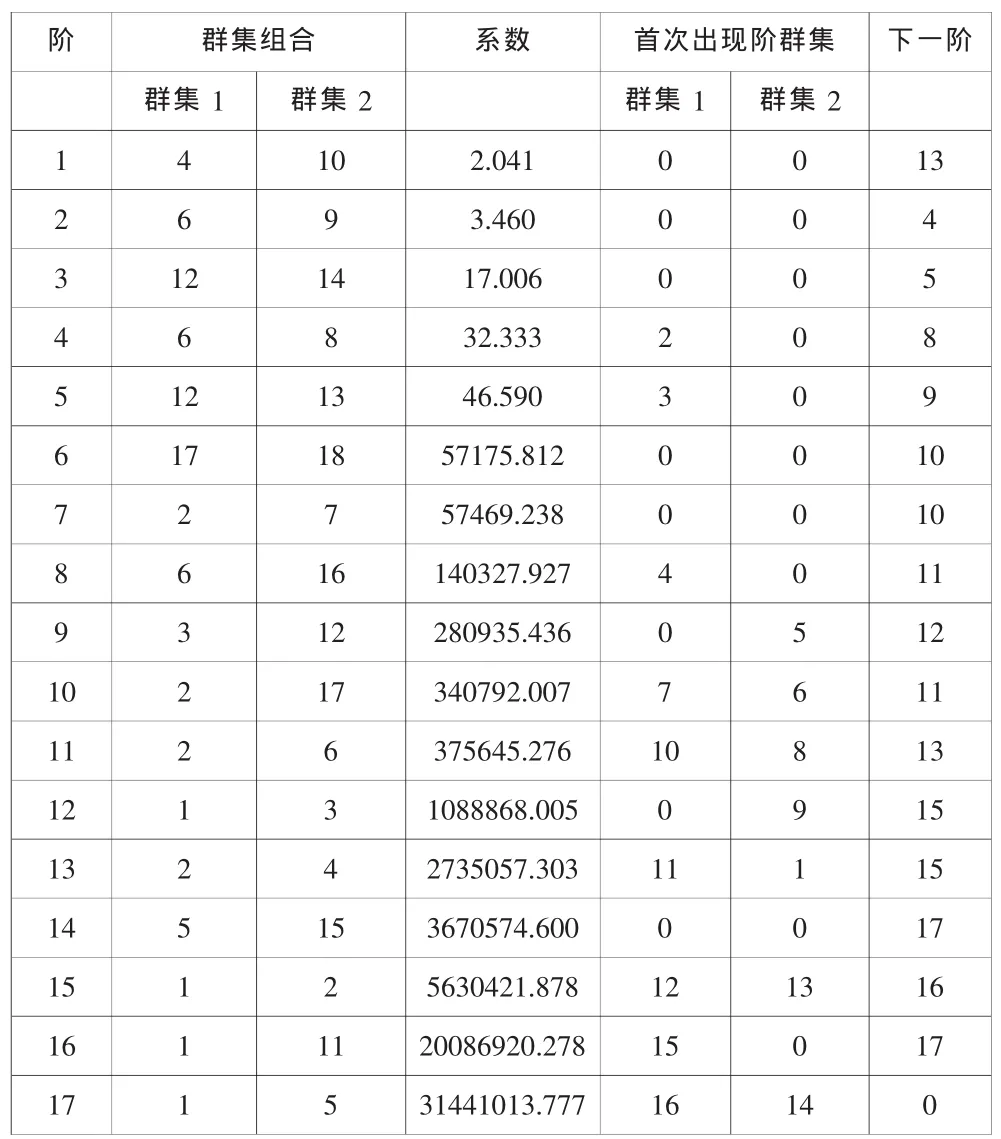
表7 聚类表

主成分分析法结果表明，绿化树种的生理指标可以分为三类:光合作用成分，气体交换吸收成分和根系微量元素吸收成分.每种成分中所包含的变量都是正相关的，故在环境保护与改善、城市规划、住宅区绿化、园林设计选择树种选择树种或对绿化效果进行评价时，可以根据设计规划要求的效果，只需从三个主要指标进行考虑，诸如:重点关注滞尘量或者铅硫吸收量等，大大简化了树种选择的难度和评价复杂性.

聚类分析结果表明，根据现有树种实际功效可以将绿化树种分类，以本文为例，在环境保护研究中，将所有各类绿化树种进行分析，找出各个绿化树种之间的相互替代性，进而在实际运用中，在同类要求的绿化标准下，选择该类中成本最低的树种，能够大大降低绿化建设的成本，提高绿化效益，带来巨大的经济效益.

［1］李永杰.北京市常见绿化树种生态效益研究[D].河北农业大学，2007.

［2］梁淑英.部分城市绿化树种的生理特性及其对大气污染的响应[D].南京林业大学，2008.

［3］韩焕金.城市绿化树种生态功能研究[D].东北林业大学，2002.

［4］王海燕.呼和浩特市10种主要园林树木生理生态特性与生态效益研究[D].内蒙古农业大学，2009.

［5］李英，裴佳音.基于聚类分析的居民自愿供给城市森林生态服务研究[J].福建:林业经济问题，1005-9709(2008)03-0223-05.

［6］黄胜,王斌,丁桑岚,陈秀眉,陈德川.主成分分析法在二滩水质监测数据综合分析中的应用实例[J].重庆环境科学，2003，25(2):53-56.

［7］温淑瑶，王京，丁根宏.应用主成分分析法评判湖泊营养类别[J].河海大学学报，1997，25(4):86-90.

［8］汪应洛.系统工程[M].北京:机械工业出版社，2009:54-60.

［9］吕海龙,董希斌.基于主成分分析的小兴安岭低质林不同皆伐改造模式评价[J].北京:林业科学，1001-7488(2011)12-0172-07.

［10］张莉.南京常见道路绿化树种的环境效益研究[D].南京林业大学，2007.

［11］梁淑英.南京地区常见城市绿化树种的生理生态特性及净化大气能力的研究[D].南京林业大学，2005.

［12］唐东明.聚类分析及其应用研究[D].电子科技大学，2010.