乌岩岭保护区NDVI空间格局尺度及异质性分析

周蔚张小伟

（1 国家林业局华东林业调查规划设计院 浙江杭州 310019；2 浙江省森林资源监测中心 310020）

乌岩岭保护区NDVI空间格局尺度及异质性分析

周蔚1张小伟2*

（1 国家林业局华东林业调查规划设计院 浙江杭州 310019；2 浙江省森林资源监测中心 310020）

基于TM影像提取的乌岩岭NDVI数据，采用空间统计学中Moran’s I和半变异函数分析的方法，选择适宜尺度，并在该尺度上对乌岩岭NDVI的空间格局研究。研究结果表明：（1）通过对各尺度上的Moran’s I和半变异函数的分析得到一个较佳空间自相关分析尺度为650m；（2）乌岩岭风景区NDVI具有显著的空间自相关性在650m的尺度上，其空间自相关指数为0.16，且Z值为4.51，这说明乌岩岭风景区植被空间关联性很强；（3）利用半变异函数对乌岩岭的NDVI进行全局空间分析，在650m的尺度上，NDVI的变程为1244.6m，即研究区具有空间自相关NDVI值的最大距离为1244.6m。

乌岩岭；NDVI；空间自相关性；Moran’sI；半变异函数

近年许多学者投入到植被的空间结构性研究中去，植物种群的空间分布特征以及环境因子对植物种群空间分布的影响，已成为生态学者广泛关注的问题[1-3]，也有部分学者对植被空间相关性进行研究[4-6]。这些研究都是通过对植被空间结构分析以期为决策提供依据，其研究方法多采用Moran’s I和半变异函数分析等方法。本文通过对研究区TM影像NDVI的Moran’s I和半变异函数分析来研究乌岩岭保护区植被的空间自相关性，为该景区空间格局研究奠定基础。

1 研究区概况

乌岩岭国家级自然保护区位于浙江省泰顺县的西北部，西与福建省的寿宁、福安接壤，北接浙江省的文成县、景宁县。地理位置处在北纬27°20＇52″—27°48＇39″，东经119°37＇8″—119°50＇00″。保护区范围除垟溪保护站外，其他均集中连片，总面积18861.5hm2。

乌岩岭自然保护区地处浙南沿海山地，属“南岭闽瓯中亚热带”气候区，温暖湿润、四季分明、雨水充沛，具中亚热带海洋性季风气候特征。保护区内森林植被在全国植被分区属中亚热带常绿阔叶林南部亚地带。由于独特的自然地理条件，加上地处偏远高山，人烟稀少，保存有大面积原生性常绿阔叶林。

2 数据预处理

2.1 辐射校正

本研究使用2010年8月LANDSAT卫星TM数据为遥感数据源。由于电磁波在地表到传感器的传输过程中受大气中水汽、灰尘及气溶胶影响，使得传感器获取的原始信息与地表真实反射率相比有一定程度的失真，需要通过辐射校正进行修正。

辐射校正按照校正后结果分为绝对校正和相对校正。绝对校正是指将遥感图像的DN值转换为地表反射率或地表反射辐亮度；相对校正是指使影像相同DN值表示相同地物反射率而不考虑地物的真实反射率。本文通过单幅影像提取NDVI进行空间格局尺度及异质性研究，因此对TM影像进行绝对辐射校正以获取真实NDVI值。

辐射校正方法包括不变目标法、直方图匹配法、黑目标法、 ContrastReduetion法、综合大气校正法、辐射传输模型法等。其中，利用电磁波在大气中的辐射传输原理建立辐射传输模型进行辐射校正是精度较高的一种。常用的辐射传输模型有6s模型、LOWTRAN模型和MORTRAN模型等。本文采用6s模型进行辐射校正。

2.2 几何校正

采用GPS采点与1:1万地形图相结合的方式对研究区影像数据进行几何精校正，选取46个明显地物点作为控制点，控制点残差精度控制到0.3。由于本文采取的研究方法是选取不同尺度的NDVI值作为研究数据，对影像DN值的真实性要求较高而连续性要求不高，因此采用最邻近法进行重采样。

3 研究方法

根据Tobler地理学第一定律[8]，即所有的事物都是相互联系的，但是离得越近的事物，彼此之间的联系越强。本文对经过辐射校正和几何校正的研究区TM数据在100m-750m不同尺度下进行NDVI值提取，并采用Moran’s I和半变异函数ɣ对乌岩岭风景区的NDVI空间结构进行分析。

3.1 空间自相关的量化指标Moran’s I

Moran’s I指数是常用的空间相关性量化指标之一。Moran’s I可以简单定义如下[10]：

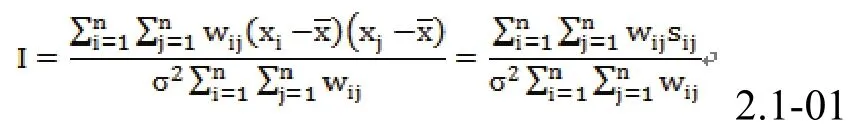
式中，xi和xj是变量x在相邻配对空间单元的取值，¯x是变量x的平均值，wij是二元对称空间权重矩阵，n是空间单元总数， σ为标准差。I指数的取值在-1到1之间，其中-1表示极强的负空间自相关，1表示极强的正空间自相关，取值0表示不相关。从地学角度来理解，如果I指数为正值，表示植被覆盖类型倾向聚集，空间分布具有较好的整体性；反之，则表示空间分布呈现破碎化。

把随机情况下的Moran’s I指数的期望值表示为EI：

EI的取值始终为负值，且EI与单元数n反向变动，因此区域单元的规模越大，EI的绝对值就越小。但当空间规模（n）较小时，EI可能是一个绝对值较大的负值，此时不能轻易的认为存在较强的负空间自相关。

Moran’s I在随机假设条件下的方差VAR(I)为：

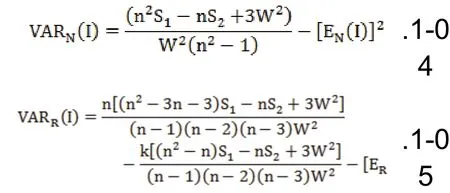
式中k表示变量x的峰度，正态分布曲线的尖峭程度。

通过莫兰指数显著性校验公式计算标准化Z 值：

3.2 半变异函数ɣ

半变异函数理论由应用数学专家Matheron G创立，是地统计学理论的重要组成部分。半变异函数ɣ（h）通过测算两点空间属性的变异程度与两点间距的关系来描述要素的分布特征[11-12]。在一维的情况下，半变异函数被定义为区域化变量Z(x) 在点x 和x + h 处的值Z(x)与Z (x + h) 差的方差的一半为区域化变量Z (x)在x 轴方向上的半变异函数,记为ɣ (h) ,即

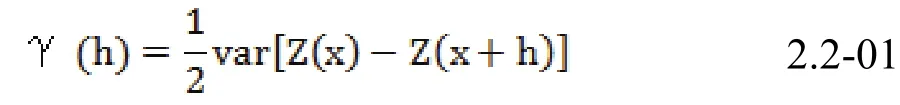
在满足二阶平稳假设的条件下，有22.2-02

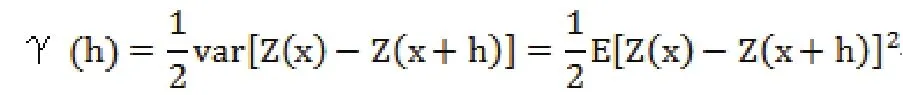
半变异函数可以产生3个基本参数，即块金值、基台值和变程。所谓块金值也叫块金方差，根据半变异函数定义，当h=0时，其半变异函数值应为0，然而在实际的样本变半异函数计算过程中，其近似平滑曲线并不通过原点，而是具有一个正的截距，将其定义为块金方差。半变异函数是一个单调递增的函数，即ɣ(h)随着h的增大而增大，当h超过某一个范围时，半变异函数ɣ (h)的值不再增大，在一个极限值附近摆动，这个极限值被称为基台值或者阈值。所谓变程是指随着h的增大，空间上Z(x)与Z (x + h)之间的相关性逐渐减小以至于消失这个过程中的h值。在地学应用中，以块金值与基台值的比值表示随机因子与结构因子对空间总变异的影响，比值大则结构因子影响大，比值小则随机因子影响大。当区域化变量在空间的变异性仅随着距离而改变，而与方向无关时，称为各向同性，否则则称为各向异性。

4 结果与分析

4.1 研究尺度选择

自相关性和尺度是密不可分的，本研究分别采用100m-750m多个尺度来分析比较乌岩岭风景区植被空间自相关性的较佳尺度。通过对各尺度的Moran’I、Moran’I的显著性检验指标Z值、半变异函数的变程以及半变异函数块金值进行比较分析，从而获得一个较佳尺度。

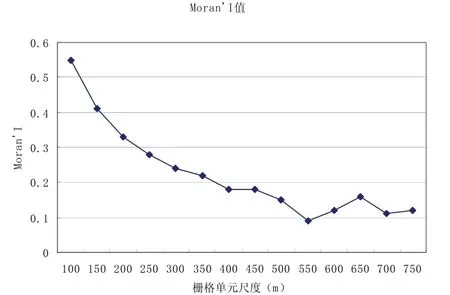
图1

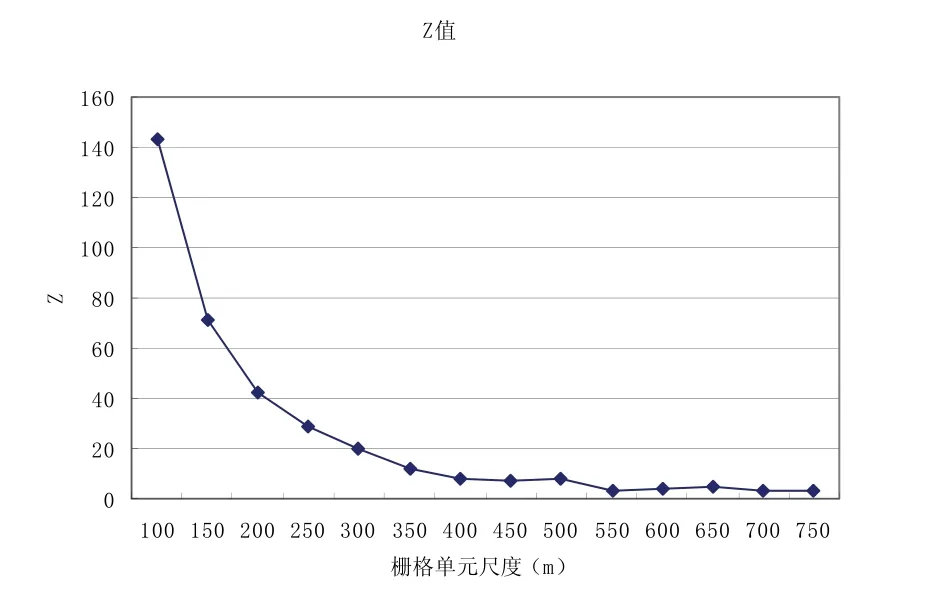
图2

图1、和图2分别为各尺度上NDVI值的Moran’I值及各尺度上Moran’I的标准化Z值。从图3-1和图3-2不难看出随着尺度的增大NDVI值的自相关指数和显著性指标Z值都呈现出下降趋势，即相邻空间单元之间距离越大，其空间自相关性越小。在尺度为650m时，Moran’I值有所反弹，达到0.16，之后再次下行。尺度为700m和750m时的Z值分别是3.37（大于2.58）和2.56（小于2.58），说明显著的空间自相关性的尺度分界线在700m和750m之间。

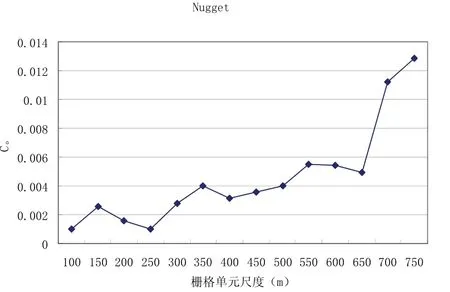
图3

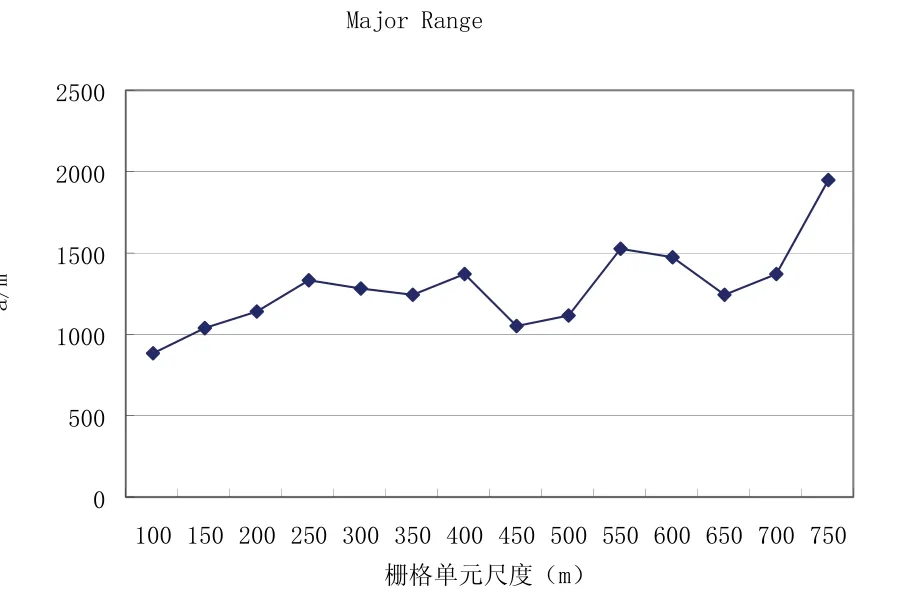
图4

图3和图4分别是以球状模型计算各尺度上的全局半变异函数的块金值和变程值结果。前者表示一定尺度上乌岩岭地区NDVI的变化量的随机性大小，后者表示乌岩岭地区NDVI自相关范围大小[13]。从图3-3和图3-4可以看出，块金值在显著自相关时维持在0.004左右，650m尺度后，块金值急剧上升，随机因子影响迅速增大。变程在具有显著自相关时基本上稳定在1000m-1500m之间，650m尺度后也陡然上升，这里的变程已经没有意义。

根据Tobler地理学第一定律[7]，较小的尺度不具有典型性，综合考虑自相关分析及半变异函数分析结果，选择650m这个尺度作为对乌岩岭植被结构分析的最终尺度。

4.2 空间异质性分析

在650m的尺度上，由Moran’s I的计算结果可以得到，乌岩岭风景区植被空间自相关性显著，其全局Moran’s I指数为0.16，而Z值为4.51，Z值远大于显著性为99%的临界值2.58。进一步计算各方向上Moran’s I值（表1），在西南-东北方向上Moran’s I值最大，呈显著正相关，而东南-西北方向上Moran’s I值较小。乌岩岭风景区在东北-西南方向上植被整体性良好，而在东南-西北方向上受水体及人为因素影响，植被相对破碎。

表1 乌岩岭保护区各方向Moran’s I值

对650m尺度上的NDVI值做半变异函数运算，得到变程为1244.6m，块金值为0.00494718，块金值/基台值为0.374644。即当两个样本点的距离相距1244.6m以上，这两点就不在具有空间自相关性。乌岩岭风景区NDVI的空间分布中随机因子影响较小，随机因子导致的空间变异占系统总变异的0.49%；结构性因子占主导地位，结构性因子导致的空间变异占系统总变异的99.51%。

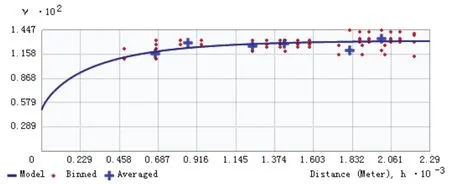
图5

4.3 结论

本文以TM影像为数据源，利用空间统计学方法，对乌岩岭风景区进行Moran’s I值分析和半变异函数分析，研究了其植被覆盖在空间分布上的相关性及空间变异特征，可以得到如下结论：

1）乌岩岭风景区NDVI具有显著的空间自相关性。通过对乌岩岭NDVI进行Moran’s I分析，可知其空间自相关指数为0.16，且Z值为4.51，这说明乌岩岭风景区植被空间关联性很强，相似的NDVI值倾向于聚在一起，不同的林分聚集性较强，具有较好的整体性。

2）通过对各尺度上的Moran’s I和半变异函数的分析得到一个较佳尺度为650m，并在这个尺度上对乌岩岭地区的NDVI空间结构性进行分析。

3）利用半变异函数对乌岩岭的NDVI进行全局空间分析，从结果来看，在650m的尺度上，NDVI的变程为1244.6m，即研究区具有相似NDVI值的空间自相关距离为1244.6m。

4）乌岩岭风景区的NDVI值存在各向异性的分布特征，在东北-西南方向上呈显著自相关，相似植被类型沿带状分布。

[1] LAAKA-LINDBERG S,HEDDERSON T A, LONGTON R E. Rarity and reproduction characters in the British hepatic flora [J] .Lindbergia, 2000,25:78-84.

[2] HEDENAS H,ERICSON L.Epiphytic macrolichens as conservation indicators: Successional sequence in Populus tremula stands [J]. Biol Conserv,2000, 93:43-53.

[3] 常新华,赵秀海等.长白山针阔混交林主要树种空间分布及其环境解释[J].北京林业大学学报, 2009(1): 7-12.

[4] 钱亦兵,吴兆,杨海峰等.古尔班通古特沙漠纵向沙垄植被空间异质性[J].中国沙漠,2011(2):420-427.

[5] 彭晚霞,宋同清,曾馥平等.喀斯特常绿落叶阔叶混交林植被的空间异质性[J].西北植物学报，2011(4):815-822.

[6] 左小安,赵学勇,赵哈林等.沙地退化植被恢复过程中植被的空间异质性[J]. 生态环境学报,2010(7): 1513-1518.

[7] 余明.生态环境综合信息图谱生成与应用[M].北京市:测绘出版社,2008:38-90.

[8] Tobler W. A computer movie simulating urban growth in the Detroit region[J]. Economic Geography, 1970, 46:234-240.

[9] Cliff A D,J K Ord. Spatial Processes: Models and Applications[M]. London: Pion,1981.

[10] David W.S. Wong Jay Lee. Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS[M].北京市:中国财政经济出版社, 2008: 337-342.

[11] 张雪艳,胡云峰,庄大方等.蒙古高原NDVI的空间格局及空间分异[J].地理研究,2009（1）:10-18.

[12] Daniel A. Griffith. Modeling spatial dependence in high spatial resolution hyperspectral data sets [J]. Geographical System ,2002(4):43-51.

[13] 冯益明.空间统计学理论及其在林业中的应用[M].北京市:中国林业出版社,2008:42-48.

TP752.1

：B

：1004-7743（2013）02-0067-05

2013-04-20