动生电动势与暂态过程

付超杰

(周口师范学院 物理与电子工程系，河南 周口 466000)

0 引言

法拉第定律说明只要闭合电路的磁通有变化，就有感应电动势。感应电动势分为动生电动势和感生电动势。通常把磁场不随时间变化而闭合电路的整体或局部在运动而产生的感应电动势叫动生电动势。动生电动势的原理、大小和方向是怎么规定的，导体杆的动生电动势的大小有一变化过程，这过程又是怎样的呢?电感中的电流都不能发生突变而是随时间按指数规律变化，指数规律变化的暂态过程存在于上述感生电动势起关键作用的动态电路中。下面，我们将用经典分析法求解导体杆动生电动势的暂态过程。

1 动生电动势

为了研究动生电动势的暂态过程，需要知道动生电动势的成因及其公式，由此确定产生的感应电动势是动生电动势还是感生电动势，以及是哪部分产生的及产生动生电动势的大小。

1.1 动生电动势的成因

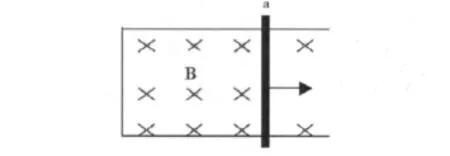
图1 ab棒在磁场中运动

1.2 动生电动势的计算

动生电动势原则上有两种计算方法。

(1)用洛伦兹力公式及电动势的定义推出的ε动=ʃ(—v×—B)·—dl计算，先在导体上选取线元—dl，再由此计算线元处速度和磁场强度，而积分便可得动生电动势。

(2)利用法拉第定律计算，有两种可能。

①闭合电路整体或局部在恒定磁场中运动，根据运动情况求出闭合电路的磁通φ与t的关系，求微商dφ/dt便得动生电动势ε。②当有一段不闭合导线在磁场中运动时，可假想一条曲线与不闭合导线组成闭合曲线，根据法拉第定律求闭合曲线动生电动势。又因为所补曲线不动及磁场不变，ε即为所求不闭合曲线的动生电动势［2］。另外，电磁感应而产生的动生电动势具有相对性［3］。

2 暂态过程

当电路的结构、元件参数和激励一定时，电路的工作状态也就一定，且电压和电流为一稳定的值，此时电路所处的工作状态就称为稳态。当电路从一种稳态转变到另一种新的稳态时，往往需要一定的时间，电路在这段时间内所经历的过程即为暂态过程。电路变化过程中的任一状态都可称为暂态。对暂态过程，一方面，我们要充分利用电路的暂态过程来实现振荡信号的产生、信号波形的改善和变换、电子继电器的延时动作等;另一方面，又要防止电路在暂态过程中可能产生的比稳态时大得多的电压或电流现象。故进行暂态分析就是要充分利用电路的暂态特性来满足技术上对电气线路和电气装置的性能要求，同时又要尽量防止暂态过程中的过电压或过电流现象［4］。

3 动生电动势的暂态过程分析

暂态分析就是要分析在激励源作用下，或者在电路内部储能的作用下，电路中各部分的电压和电流随时间变化的规律。下面就以平行金属导轨上导体杆产生的动生电动势的暂态过程作出分析，并导出求动生电动势的简易方法。

图2装置中，PQ长度为l，导体的一端连接电阻R。整个装置放在均匀磁场—B中，—B与导轨所在平面垂直。设杆以初速度v0向右运动，忽略电阻以外的电阻及导轨和杆之间的摩擦力。ε0为恒定电源电动势，根据以下几种情况计算导体杆的动生电动势。

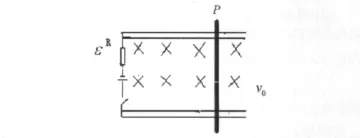
图2 PQ棒在均匀磁场中运动

3.1 动生电动势的零状态响应

杆的初速度v0=0，杆中的初始电动势为零。设开关闭合时t=0，求t≥0时导体杆的动生电动势。

设t≥0时，任一时刻导体杆的速度为v(t)，则动生电动势大小为ε(t)=Blv(t)。根据安培定律及I=和牛顿第二定律可得微分方程:mR+B2l2v=Blε0;v(0+)=0利用分离变量法解次微分方程得:v(t)=(1-e)，从而得杆的动生电动势为:ε(t)=Blv(t)=ε0(1-e)。

当t趋向于无穷时，ε(t)=ε(∞)=ε0为动生电动势的稳态值，则上式可写为ε(t)=ε0(1-)。τ称为回路的时间常数。

ε(t)的变化曲线如图3所示。可得，动生电动势在t=0时不能发生突变。

从电路的角度来看，暂态过程中动生电动势可视为稳态分量和暂态分量相加而得。当动生电动势达到稳态值时，电路的暂态过程随即终止。

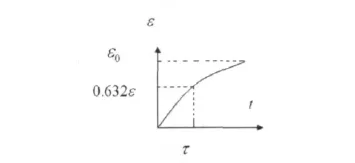
图3 动生电动势的零状态响应曲线

3.2 动生电动势的零输入响应

设此种情况下电源电动势ε0=0，开关k是闭合的，在时间t=0时给杆一向右的初速度v0。这时可建立速度的微分方程mR+B2l2v=0;v(0+)=v0。

解得动生电动势为ε(t)=Blv0=Blv(0+)当t=τ时，ε(t)=ε(τ)=0.368Blv0，即τ的物理意义是动生电动势的值减小到初始值的36.8%所需要的时间。总之，τ可看作暂态过程的“时间尺度”，从理论上讲，电路只有经过t=∞的时间才能达到稳定。但是，由于指数曲线开始变化快，而后逐渐减慢，所以，实际上经过t=5τ时间，就足可认为达到稳态了。ε (τ)的变化曲线如图4所示。

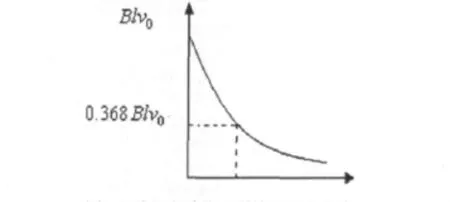
图4 动生电动势的零输入响应曲线

3.3 动生电动势的全响应

设在此种情况下ε0≠0，并在t=0时给杆一初速度v0使之向右运动，求t≥0时杆中的动生电动势。可列出关于速度的微分方:mR+B2l2v=Blε0v(0+)=v0解得动生电动势ε0(1-)+Blv(0+);前为零状态响应，后为零输入响应。则全响应的曲线应是零状态响应曲线与零输入曲线的叠加。上式可改写为ε(t)=(Blv0-ε0)+ε0，可知全响应曲线仍按指数规律变化，只是它的最大值为 ε0，最小值是趋近于Blv0。改后式的第一项为衰减指数函数，t趋于无穷大时趋于零，为暂态分量;第二项为稳态分量，即全响应=暂态分量+稳态分量。

4 求动生电动势的三要素法

据以上分析知动生电动势的响应是由稳态分量和暂太分量两部分相加而得:ε(t)=ε(∞)+［ε(0+)-ε(∞)］t，式中ε(∞)和ε(0+)分别为动生电动势的稳态值和初始值，因此，只要求得以上三个值即可列出动生电动势随时间的变化关系式，而不用再求解微分方程，故称此法为求解动生电动势的三要素法［5］。

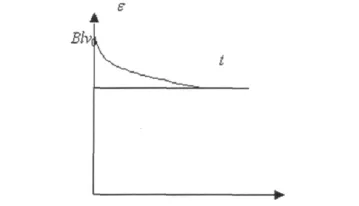
图5 动生电动势的全响应曲线

5 结语

本文根据动生电动势和暂态过程分析得出动生电动势的两种求法，利用一阶微分方程解法对动生电动势的几种响应进行了分析，得出电路的响应是由暂态分量和稳态分量两部分相加而得，且动生电动势的暂态分量按指数规律变化。从而得出用三要素法求动生电动势:无论是电路的零状态、零输入或全响应，输入量不论是恒定电源或恒力均可用三要素法方便的求出动生电动势或速度随时间的变化规律［6］。三要素法给我们提供了一种研究暂态过程的简便方法，在以后的解题中，我们应首先考虑是否能用三要素法解题。

［1］颜琳.王小云.全秀娥.动生电动势的产生机理［J］.吉首大学学报，2007，28(1):71-72.

［2］梁灿斌，秦光戎，梁竹健.电磁学［M］.北京:高等教育出版社，2004.

［4］孙国耀.动生电动势的相对性［J］.中山大学学报，2005，44:166-167.

［5］苏民.动生电动势与暂态过程［J］.殷都学刊，1994，(2):30-32.

［6］房淑芬.谈动生电动势［J］.辽宁师专学报，2000，2 (4):31-32.