枪机簧线性假设的适用性分析

杨梅森，徐万和，仲其伐

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

在自动武器工作过程中，枪机簧不断的储存能量和释放能量，保证了武器的后坐和复进到位，并且影响着自动武器的射击频率。在自动武器动力学研究时常常将枪机簧的质量转换为一个等效质量，然后用这个等效质量来算出枪机簧的振动频率。为了算出这个等效质量，一般先对枪机进行线性假设，但是线性假设与实际枪机簧的运动情况并非完全吻合的，本文研究了枪机簧计算时通常使用的线性假设的适用性。

1 线性假设分析

此时，一般忽略枪机簧的振动，假设枪机簧各圈在任一瞬间的速度沿枪机簧的长度成线性比例［1-3］，即

其中:vx—距离固定点距离x 处簧圈的速度;

l—枪机簧原长;

v—距离固定点距离l 处簧圈的速度。

现以如图1 所示的枪机簧状态为例，将机匣简化成光滑水平面，枪机簧原长为l，此时被压缩至l1处，向右运动，连接的开闭锁构件质量为M，在连接开闭锁构件处即l1处的速度为v，取向右为正。按照线性假设，此时各簧圈的速度如式(1)所示。

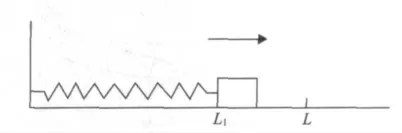
图1 平面上的枪机簧与开闭锁构件连接

将式(1)两边对时间求导，得:

其中:ax—距离固定点距离x 处簧圈的加速度;

a—距离固定点距离l 处簧圈的加速度。

将式(1)两边对时间积分，得到式(3)，因取向右为正，所以各簧圈的位移为负。

其中:sx—距离固定点距离x 处簧圈的位移;

s—距离固定点距离l 处簧圈的位移。

设枪机簧单位长度的质量为m，则距离固定端距离为x 处的那一小段长度dx 所受的合力为:

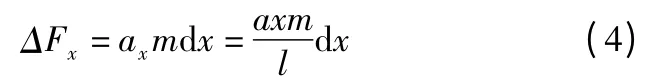
对式(4)进行积分，可得x 处的弹簧力式(5)。

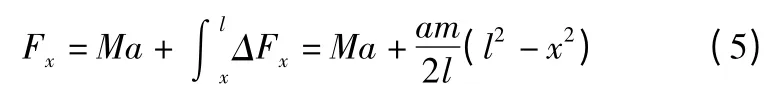
由式(5)可得x 处dx 长度的弹簧压缩量为式(6)。

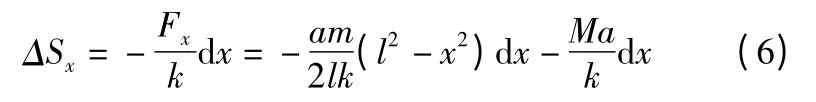
其中:k—弹簧的刚度

对式(6)进行积分，可得x 处的位移为式(7)。

式(7)和式(3)是不符的，因为枪机簧本身质量等原因，枪机簧各圈在任一瞬间的速度沿枪机簧的长度并非是成线性比例［4-5］。

由文献可知，枪机簧在有质量的条件下仍可以做简谐运动［6］，此时若枪机簧的质量m 远大于连接的开闭锁构件质量M，有:

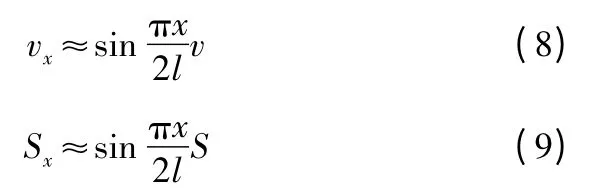
其中:Sx—到固定点距离x 处簧圈的位移;

S—到固定点距离l 处簧圈的位移。

在自动武器中，开闭锁构件的质量M 远大于枪机簧的质量m，此时可算出:

此时弹簧各圈在任一瞬间的速度沿枪机簧的长度近似成线性比例，说明书中的假设是有依据的。但是要枪机簧及开闭锁机构一起做简谐运动需要的初始条件与枪机运动实际情况下是不符合的。在子弹击发的瞬间，开闭锁构件会受到一个冲击载荷的作用，这个冲击载荷对枪机簧的作用效果会受到枪机簧本身参数的影响［7］，必然导致枪机簧实际的运动与线性假设之间存在着差别。那么这其中的差别有多大呢?现以某口径冲锋枪为例进行ABAQUS 建模，分析该普遍用于自动武器研究过程中的线性假设与建模分析结果的相同和差异性。

2 仿真比较

该冲锋枪枪机簧质量为0.03 kg，原长0.43 m，最小工作载荷长度0.3 m，刚度为21 kg/m，开闭锁构件0.53 kg，在击发后火药力作用于开闭锁构件一个大小10 000 N、时间5 e－4 s 的压力脉冲，忽略运动过程中的摩擦力。

受文献中对弹簧进行等效替代的启发［4］，仿真时，将开闭锁构件用一个边长0.01 m、质量0.53 kg 的刚性立方体代替，枪机簧用10 个边长0.01 m、质量0.003 kg 的刚性立方体和10 个长度0.02 m、刚度210 kg/m 的弹簧约束代替，如图2 所示，从而将求弹簧上各点的运动情况转变成求各立方体的运动状况。

设置11 个小立方体在y 和z 方向不可移动，最后一个枪机簧代替立方体不可沿x 正向移动。对于开闭锁构件除受到一个脉冲作用，还受到一个持续的枪机簧预压力作用。

图2 枪机簧与开闭锁构件的等效模型

因为各立方体均为刚体，所以只要求出其上一点的运动情况就可知道立方体的运动情况，故建立如图2 中粗点所示的集合。

为了求得各时刻图2 所示集合中各点的运动情况，建立一条经图2 中粗点的线段作为建立坐标时x 轴，该线段以图中所示的左边第一个粗点为起点，以右边第一个粗点为终点。

2.1 位移图

通过分析，得出了不同时刻图2 中各红点运动状态。(因本刊为黑白印刷。需要了解红点运动状态请与作者联系，下同。)时间(单位为ms)为0.05，0.1，0.175，0.287 5，0.456 25，0.709 38，1.089 1，1.658 6，2.512 9，3.794 3，5.716 5，8.599 8，12.925，19.412 和29.143 时各点的位移状态如图3 所示，随着时间的推移，运动的开闭锁构件逐渐影响到枪机簧各点，各点的位移逐渐增加，且逐渐呈线性分布，与线性假设是一致的，最后一段时间中远离开闭锁构件的部分枪机簧没有随着时间改变位移是因为后面的枪机簧挤压已经在一起。

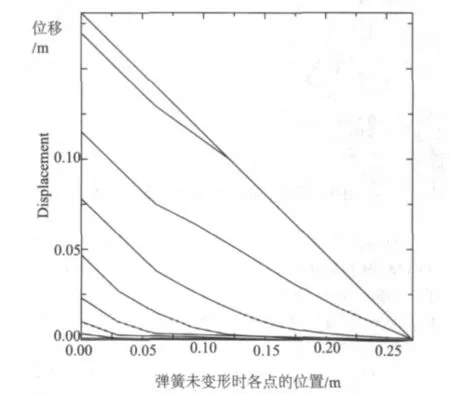
图3 不同时刻枪机簧上各点的位移

时间(单位为ms)为39.143，49.143 和59.143 时各点的位移状态如图4 所示，在这段时间内，随着时间的推移，枪机簧各点的位移逐渐减小，但总体上还是接近于线性分布的，且59.143 ms 时位移已经接近于零，即开闭锁构件已经复进完毕。

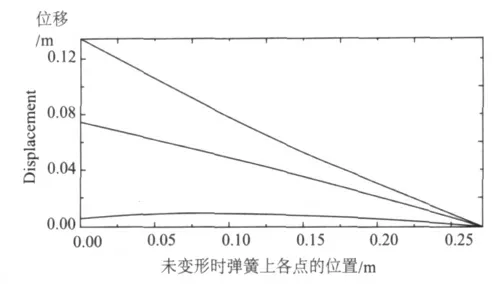
图4 不同时刻枪机簧上各点的位移

2.2 速度图

时间(单 位为ms)为0.05，0.1，0.175，0.287 5，0.456 25，0.709 38，1.089 1，1.658 6，2.512 9，3.794 3 和5.716 5时各点的速度状态如图5 所示，随着时间的推移，运动的开闭锁构件逐渐影响到枪机簧各点，各点的速度逐渐增加，且逐渐呈线性分布，与假设是一致的。

图5 不同时刻枪机簧上各点的速度

时间(单 位 为ms)为8.599 8，12.925，19.412，29.143，39.143，49.143 和59.143 时各点的速度状态如图6 所示，在8.599 8 ms 至19.412 ms 这段时间内，接近开闭锁构件的部分速度已经开始降低，但仍是正向的，整体开始接近于线性假设。

在29.143 ms 至59.143 ms 这段时间内，速度逐渐的反向增大，整体呈线性分布，与假设是一致的。

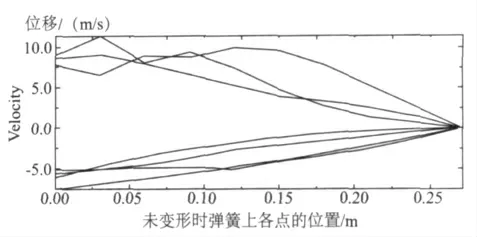
图6 不同时刻枪机簧上各点的速度

3 结语

从以上各图和分析可以看出，在整个自动武器工作过程中枪机簧各点的位移与线性假设的契合度极好;枪机簧各点的速度在相对较短的时间内与线性假设契合度不太好，但大部分时间内契合度还是比较好。由此可见，在自动武器的设计中枪机簧线性形变假设还是有很强的适应性，但如果设计中需要更准确的结果，则应该对枪机簧进行更细致地分析。

有前面的数学分析可知，开闭锁构件与枪机簧的质量比越大则枪机簧的线性形变越明显，在自动武器设计过程中，当该质量比比较小时，有必要论证引用线性假设的合理性，而当该质量比比较小时，应该根据需要论证分析采用线性假设的合理性。

在以前的文献中有一些关于弹簧运动的分析，其中大部分都是为了研究弹簧等效质量与振动周期的关系，在分析弹簧等效质量的过程中进行了较多的假设，所以最后得出的结论难免与真实情况有一定的出入。本文用仿真的方法进行分析，与以前的研究相比更接近了真实情况一步。

［1］蒋学良.弹簧动力学性质研究［J］.产业与科技论坛，2011，10(10):85-86.

［2］周俊敏，王玉梅.弹簧质量与弹簧振子振动周期关系的探讨［J］.周口师范学院院报，2009，26(5):58-60.

［3］刘吉森，李楠，李复然.非理想化条件下弹簧振子振动周期的确定［J］.高校实验室工作研究，2007(3):39-40.

［4］何连超.有质量弹簧的振动周期探讨［J］.物理与工程，2011，5(21):1-2，9.

［5］刘景世.浅议弹簧教学［J］.物理通报，2011(2):12-14.

［6］金彪.也谈弹簧质量对弹簧振子振动周期的影响［J］.中学物理，2011，29(3):62-63.

［7］郝兵，李守仁.冲击载荷下弹簧质量系统瞬态响应的近似求法［J］.哈尔滨工程大学学报，2003，24(4):427-430.