基于排队模型的β可靠性最大覆盖应急服务车辆选址：模型与算法

乔联宝，朱华桂

（南京大学 工程管理学院，南京 210093）

在现实生活中，应急服务设施的选址具有广泛的应用，如警察巡逻车、消防站救护车辆以及医院急救车辆的选址问题.早期的应急服务设施主要应用覆盖模型来确定应急服务设施点的位置，即只要在给定的时间（或者距离）范围内，服务点能够对需求点提供服务即可.如Toregas等［1］较早对应急服务设施的集合覆盖问题进行了研究，Current和Morton［2］考察了两种类型警报器的集合覆盖问题.集合覆盖选址在应用中存在一定的局限性，它所产生的设施点数量一般较多，往往超出了可能的预算约束.所以后来又出现了最大覆盖模型，最大覆盖并不要求覆盖所有的需求点，而是要在给定的资源限制下覆盖尽可能多的需求量，Church和ReVelle［3］较早地提出了最大覆盖模型.

在某些情况下，需求点与其周围最近的设施点之间的距离在给定的服务半径内，按照覆盖模型的规定，该需求点应该被设施点所覆盖.但是，并没有考虑这样一种情形：当需求点向其最近的服务设施点请求服务时，该服务单位恰好处于繁忙状态，比如正在为其服务范围内的另一个客户提供服务.那么在这种情况下，新产生的需求要么进行排队等候，要么损失了，或者转向其他的服务设施点等.在这种情况下，无论需求点进行排队等候还是损失了，它都不在一般覆盖模型的考虑范围之内.

鉴于服务器因处于繁忙状态而不能够对其他需求提供服务，Daskin［4］提出了最大期望覆盖选址问题（Maximum Expected Covering Location Problem，MEXCLP），最大化能够得到服务的需求量的期望值.ReVelle和Hogan［5，6］提出了有服务水平保证的最大覆盖选址模型，要求被覆盖的需求点能够得到服务的概率不小于给定的值α.同确定性覆盖模型假定所有被覆盖的需求点都可以及时得到服务相比，概率覆盖模型在假设条件上有很大的进步.但是，以上等人所建立的概率覆盖模型要求服务器的繁忙率必须事先已知，而且相互独立，显然这些假定仍然过于严格.

对于服务器经常处于繁忙状态的设施选址问题，使用排队论模型来研究此类问题能够更准确地反应现实系统的运行情况.在模型假设条件上也不需要假定服务器是否繁忙是相互独立的.Larson［7，8］提出了超立方排队模型来直接计算车辆的繁忙比率，但是超立方排队模型需要设施点的位置已知，并且该模型是非线性的，精确方法计算量也非常大，它常常同其他方法结合起来使用.后来一些文献直接应用排队论模型来研究服务设施经常处于繁忙状态的覆盖选址问题［9，10］，本文将从另一个角度建立有服务水平保证、基于排队论的最大覆盖选址模型.

1 相关文献综述

在设施选址模型中，Church和ReVelle［3］提出的最大覆盖模型是其中的一个重要类型，它在实践中已被成功的应用，并被广泛应用到应急服务设施的选址问题中.在基本的覆盖模型基础上，后来产生了各种不同的变化形式.早期Schilling等［11］按照集合覆盖和最大覆盖这两种类型对覆盖选址问题进行了综述；Farahani等［12］对Schilling等综述以后的近20年间与覆盖选址相关的文献做了全面而广泛的综述.以上两篇综述性文章涵盖了覆盖选址问题的大部分方面，相关问题可以参考上述文献.

早期的选址文献在模型参数方面都是确定性的.当考虑不确定因素时，Snyder［13］研究了在不确定环境下的选址问题，包括不确定环境下的决策制定.Boffey等［14］对服务台不可移动且有容量约束的排队情形下的选址问题做了相关综述，他们以确定性的p－Median问题为基本模型，通过对参数和约束的扩展逐渐将其演变为其他非确定类型的选址问题.

在最大覆盖选址问题中最早引入不确定性因素的是Daskin［4］，同样他也做了很多有助于简化问题的一些假设，比如服务器的繁忙率事先可以确定，服务器的繁忙率不依赖于最终的位置和工作量等.后来，ReVelle和Hogan［6］提出了有可靠性水平保证的，最大化车辆可获得性条件下的覆盖选址问题，并分别使用系统层次和区域层次的车辆繁忙率对实例城市进行了研究.

考虑到系统可能存在的拥堵情形，直接运用排队模型来研究应急车辆选址问题的有Marianov和ReVelle［9，10］，他们都通过运用排队论模型来进一步放松“各个服务台是否繁忙是相互独立的”这一假设条件，最大化有可靠性水平保证的需求数量.

Berman和Drezner［15］考虑了需求和服务时间都是随机的网络选址问题，需求点和设施点只位于网络的节点上，目标函数是最小化服务器到达需求点的运行时间和在服务器的平均等待时间之和，因此属于有排队系统的中值选址问题.Aboolian等［16］建立了与Berman和Drezner类似的排队选址模型，同时他们允许在一个站点设立多个服务台，并且目标函数最小化最大运行时间和等待时间之和，因此属于中心排队选址问题.Baron等［17］研究了需求随机、有等待时间约束的更一般条件下的随机选址问题，在他们的模型中，需求和服务过程都服从一般的分布，设施的潜在位置未知且有容量约束，同时对最大的到达时间和服务水平有一定要求，最后构造了求解问题的分解算法.

求解基于概率模型的覆盖选址问题所面临的一个重要难点是服务器繁忙率的确定.为了保证达到事先给定的服务水平约束，必须要求服务器繁忙率已知，而各个服务器繁忙的具体情况又依赖于设施点所处的位置.所以，文献要么假定所有服务器的繁忙率事先已知［4］，要么基于系统层次或区域层次对不同位置的繁忙率进行估计［5，6，9，10］，也有的文献通过迭代或其他改进方法来近似估计服务器的繁忙率［18］等.Larson［7］从理论上描述了如何精确计算服务器繁忙率及服务系统其他重要参数的方法，由于该方法很难应用于大规模问题，所以出现了Larson［8］的简化版，简化方法所求得的解同精确解的误差随着服务器的数目增加而减少，并不超过2%，但是该方法需要设施点位置已知.

基于上述原因，下面将建立有服务水平β保证、基于排队模型的应急服务车辆最大覆盖选址模型.由于引入了排队论模型，因此不用假定设施点的服务器繁忙与否是相互独立的.在服务器繁忙率的选择上，使用基于设施点区域水平的值.但是与以往文献不同的是模型建立的角度，本文从覆盖量的角度给出服务水平约束条件.模型M1的建立十分自然，由于是非线性规划模型，它求解起来较为困难.模型M2是整数线性规划问题，同M1相比较容易求解.但是对于求解大规模的问题，在时间上可能不可行.当需求可以分散服务，并且设施点允许安排的服务器数量无上限时，根据排队论的性质设计了相应的快速求解算法.在以下的章节中，将不再区分服务器和应急服务车辆这两个概念.

2 模型建立

从假定系统内所有服务器具有相等的繁忙率到假设不同的区域有不同的繁忙率，这在假设条件上有很大的改善，所以以下模型选择区域水平的服务器繁忙率.以往研究有服务水平保证的覆盖模型大多是直接以机会约束的形式给出服务水平约束条件，本文从覆盖量的角度来规定这一约束.

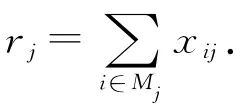
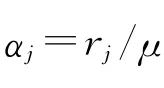
变量含义如下：

xij＝需求点i分派到设施点j的需求量；

M是一个充分大的数，其余符号如上文所述.

（2）式和（3）式表明需求点的需求量只能分派到服务半径内的设施点；（4）式要求只有在设施点至少安排了k－1台服务器时，它才有可能至少安排了k台服务器；（5）式是服务器数量关系；（6）式是允许安排的总服务器的数量；（7）式表明只有设施点建立了，它才能对其他需求点提供服务；（8）式保证只有服务站点能够对周围的需求提供规定水平的服务时，此部分需求才被计入目标函数中；（9）式和（10）式是相应的变量取值范围约束.

观察目标函数（1）式和约束（8）式，可以发现这是一个非线性规划模型，同时（8）式中变量出现在下标和求和符号中，所以该模型不能通过一般的数学优化方法或者规划软件进行求解.虽然M1模型求解起来很困难，但是它提供了直接针对服务器繁忙率建模的描述性模型.在目标函数（1）式和约束条件（8）式中，如果令β＝0，则所有zj＝1满足约束条件（8）式，因此该问题等价于不考虑服务器是否繁忙的最大覆盖问题.当β≠0时，只有满足约束1－Pyj≥β的设施点j的覆盖量才被计入目标函数.所以，为了使目标函数达到最大，既要尽可能多的覆盖，同时还要使覆盖这些需求的服务器繁忙水平不超过1－β（使得尽可能多的zj＝1）.基于上述分析，如果可以保证分派到某个设施点的需求不会使得该设施点的服务器繁忙率超过1－β，那么这种分派方法所得到的需求都会被计入目标函数中.

由于Pyj是所有yj台服务器全部繁忙的概率，因此也是系统的呼叫损失率，为了使1－Pyj≥β，也即Pyj≤1－β，一方面可以增加服务器的数量；另一方面也可以减少服务的需求量.由于需求可以部分满足，所以对于任意正整数k台服务器，总可以找到与之对应的惟一最大需求量使得恰好Pk＝1－β，这也是在k台服务器时能够保证服务水平的最大可处理需求量.如果记MAXk为使得Pk＝1－β成立的最大需求量，同时要最大化单位时间内能够得到服务水平保证的需求量，则可以得到第二个模型M2：

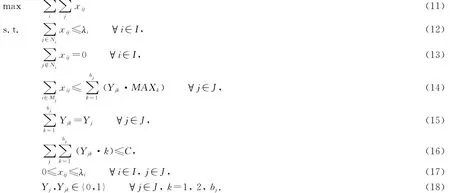
符号含义如下：MAXk＝k台服务器在满足服务水平约束时能够处理的最大需求量.

各变量含义如下：其他符号如前文所述，应当注意，此处的Yjk和模型M1中的yjk含义并不相同.

（12）式和（13）规定了需求分派的方式和范围；（14）式限制了每个设施点能够服务的最大需求量；（15）式要求只有设施点j建立了，才可能够向该设施点分派服务器，并且只能有一种分派方式；（16）式要求各个设施点服务器的总和不应超过可得到的服务器数量；（17）式和（18）式是相应的变量范围约束.由于（14）式保证了每个设施点服务的需求都不低于给定的服务水平，所以目标函数（11）式简化为最大化这种可行的需求分派量.

模型M2是一个混合整数线性规划问题，比起M1模型，它求解起来要相对容易，可以通过已知的覆盖选址算法进行求解，也可以直接利用优化软件进行求解.在下面的部分，本文将根据排队论的性质设计出在设施点的服务器数量无限制时所对应的贪婪算法.

3 算法设计与求解

3.1 算法设计

首先考虑这样一种情况，对于固定的某一覆盖量，如果存在两种（或几种）不同的覆盖方法，为了达到特定的服务水平，其中的一种方法所需要的服务器数目较少，或者使用相同数量的服务器，它能提供更高的服务水平，那么这种方法所达到的覆盖量一定要更接近最优值.由于Pyj是所有yj台服务器全部繁忙的概率，因此也是系统的呼叫损失率，合理的想法就是找到这样一种覆盖方法：在同等的覆盖量或者资源条件下，它的呼叫损失较小，从而这部分覆盖量更可能被计入目标函数.下面给出基于M／M／k／k排队系统的一个性质.

性质1 如果到达率为λ，单台服务器的服务率为μ，服务器数量为k（k≥2），则k台服务器集中服务的M／M／k／k系统要比k个分散服务的M／M／1／1系统具有较小的呼叫损失率.

证 M／M／s／s损失系统：假定顾客到达率服从参数为λ的泊松分布，每台服务器的服务时间服从参数为μ的指数分布，服务器个数为s，系统容量为s.记pk为系统有k台服务器处于繁忙状态，则根据系统平衡状态的转移方程可以得到：

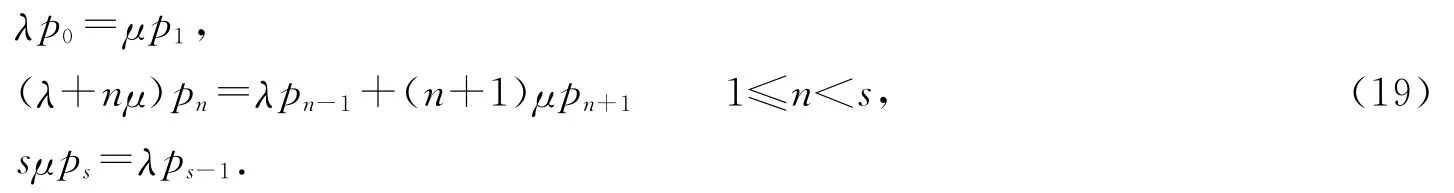
如果令α＝λ／μ，通过迭代求解式可以解得

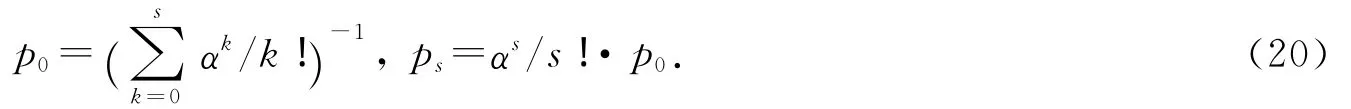
因此对于M／M／1／1系统有

现在假如将s台服务器分开单独服务，则平均每台服务器所对应的顾客到达率和它处于繁忙状态的概率为

令Δs＝p1－ps，现在证明对于任意的α＞0，s≥2有Δs＞0.

故对任意α＞0，s≥2有p1＞ps.

由上述性质可知，对于同样的需求量，应尽可能将所有的需求集中起来服务，这样可以保证较小的呼叫损失率（从而1－Pk更大）.根据上述性质，同等条件下集中服务能够提高服务水平，下面将根据性质1设计求解问题的贪婪算法.算法假定单个设施点允许安排的服务器数量无限制，当单个设施点允许安排的服务器数量相对较大时，该假设是合理的.

下面为了叙述方便，先提出以下几个概念.

最大分派覆盖量：设施点的最大分派覆盖量是所有在该设施点的覆盖半径内，且还未被分派的需求点的需求之和，记为MACQ；

实际覆盖量：设施点的实际覆盖量是在其覆盖半径内，实际分派给该设施点的所有需求之和，记为ACQ；

冗余覆盖量：设施点的冗余覆盖量等于最大分派覆盖量减去实际覆盖量，即RCQ＝MACQ－ACQ；

边际贡献量：设施点的最后一台服务器的边际贡献量是该设施点的实际覆盖量与其当前服务器数量减少1台时所能覆盖的最大量之差，如果记设施点的服务器数量为N，则MCQ＝ACQ－MAXN－1；

增加上限：设施点的增加上限是当前数量台服务器所能覆盖的最大量与实际覆盖量之差，即AUB＝MAXN－ACQ，N是设施点的服务器数量.

冗余覆盖量反映了能够覆盖但未被覆盖的需求量，这部分需求量是当服务器数量增加时可以进一步覆盖的量；增加上限是设施点在当前给定数量服务器条件下，所能够进一步覆盖的最大需求量，它反映了设施点剩余的覆盖能力.

下面给出算法的具体实现步骤：

Init：初始化潜在设施点的相关参数，包括最大分派覆盖量、实际覆盖量、冗余覆盖量、边际贡献量以及增加上限.

Phase1：

Step1：判断当前可以使用的服务器数量是否为零，或者潜在设施点能够覆盖的需求是否为零，如果是则Stop；

Step2：计算所有未建立的潜在设施点的最大分派覆盖量，并选择其中的最大者Fk，其最大分派覆盖量为MACQk；

Step3：标记设施点Fk已经建立，如果剩余的服务器数量不足以覆盖设施点Fk的最大分派覆盖量，则分派所有的服务器到该设施点；否则，分派n台服务器到该设施点，其中n满足｛n｜MAXn－1＜MACQk，MAXn≥MACQk｝.设置Fk覆盖半径内的所有需求量为零，更新可以使用的服务器数量及设施点的相关参数，返回Step1.

Phase2：

记F1，F2，…，Fq为第一阶段顺序建立的设施点，q是建立的设施点个数.

1.Demand Moving：

Step1：选择Phase1生成的最后一个设施点Fq，判断它的冗余覆盖量是否为零，如果是则Stop；否则从前q－1个设施点中选择边际贡献量最小的设施点Fi，令k＝1；

Step2：选择Fi后面的第k个设施点Fi＋k，如果两者的共同覆盖区域有公共需求点并且可以转移的最大需求量不为零，则转移该部分需求，更新设施点的相关参数；

Step3：判断设施点Fi的边际贡献量是否非正，或者Fi＋k是否等于Fq，如果是，转Step4；否则令k＝k＋1，返回Step2；

Step4：如果设施点Fi的边际贡献量小于设施点Fq增加一台服务器所产生的需求增加量，则将设施点Fi最后一台服务器移动到Fq处，更新设施点的相关参数，返回Step1；否则Stop.

2.Server Moving：

Step 1：在未建立的潜在设施点中，选择最大分派覆盖量最大的设施点fk，其最大分派覆盖量为MACQfk，如果MACQfk＜MAX1，Stop；否则，转Step2；

Step2：令K＝argn｛MAXn≤MACQfk，MAXn＋1＞MACQfk｝，K＝min｛K，q｝；对已经建立的设施点按照其最后一台服务器的边际贡献量升序排序，排序后的设施点记为I1，I2，…，In；

Step3：令K＝argmaxn｛MAXn／n≥MCIn｝，如果K＝Ø，Stop，否则将设施点I1，I2，…，In的最后一台服务器移动到设施点fk，标记建立设施点fk并更新设施点的相关参数，Stop.

3.2 计算实例

为了验证模型和算法的有效性，假定在平面上存在N个需求点，每一个需求点都可以作为潜在的设施点，并且每个需求点单位时间的需求参数λi由［1，10］之间的整数均匀分布产生，需求点的纵横坐标服从［1，100］之间的整数均匀分布.

假定服务器数量等于需求点的个数N，所有服务器具有相同的服务率μ＝θΛ／N，其中Λ为总需求，θ为参数分别取1.05和1.15（对应的系统利用率大约分别为95%和85%）；服务半径S分别取：σ－5、σ－10和σ－15，其中σ为所有需求点距离的标准差；给定的服务水平β分别取95%，80%.

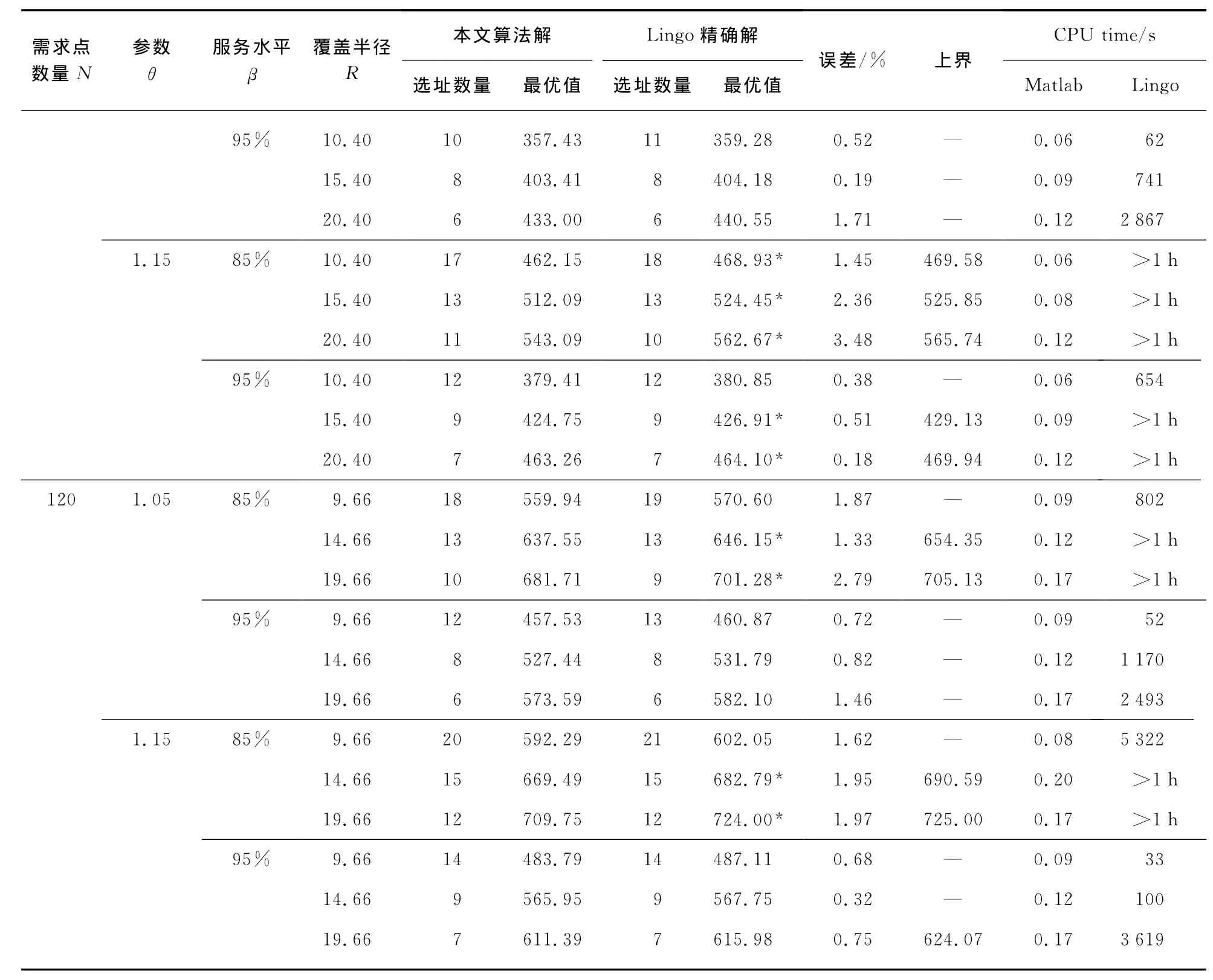
以上算法和M2问题分别通过Matlab R2012a和Lingo11.0编程实现，并在个人电脑Lenovo－R400上运行（CPU 2.40Ghz，内存2G）.表1给出了在不同问题规模时，上述算法和Lingo程序的计算结果.其中最优值列加星号的部分为Lingo程序运行1h以上给出的可行解（在给定时间1h未求得最优解），同时上界列是Lingo给出的最优目标函数值上界.误差列是上述算法最优解同Lingo程序最优解（或可行解）之间的差异.CPU time列的Matlab子列为上述算法求解时间（取Matlab第二次运行时间①），Lingo列为Lingo程序运行时间②.

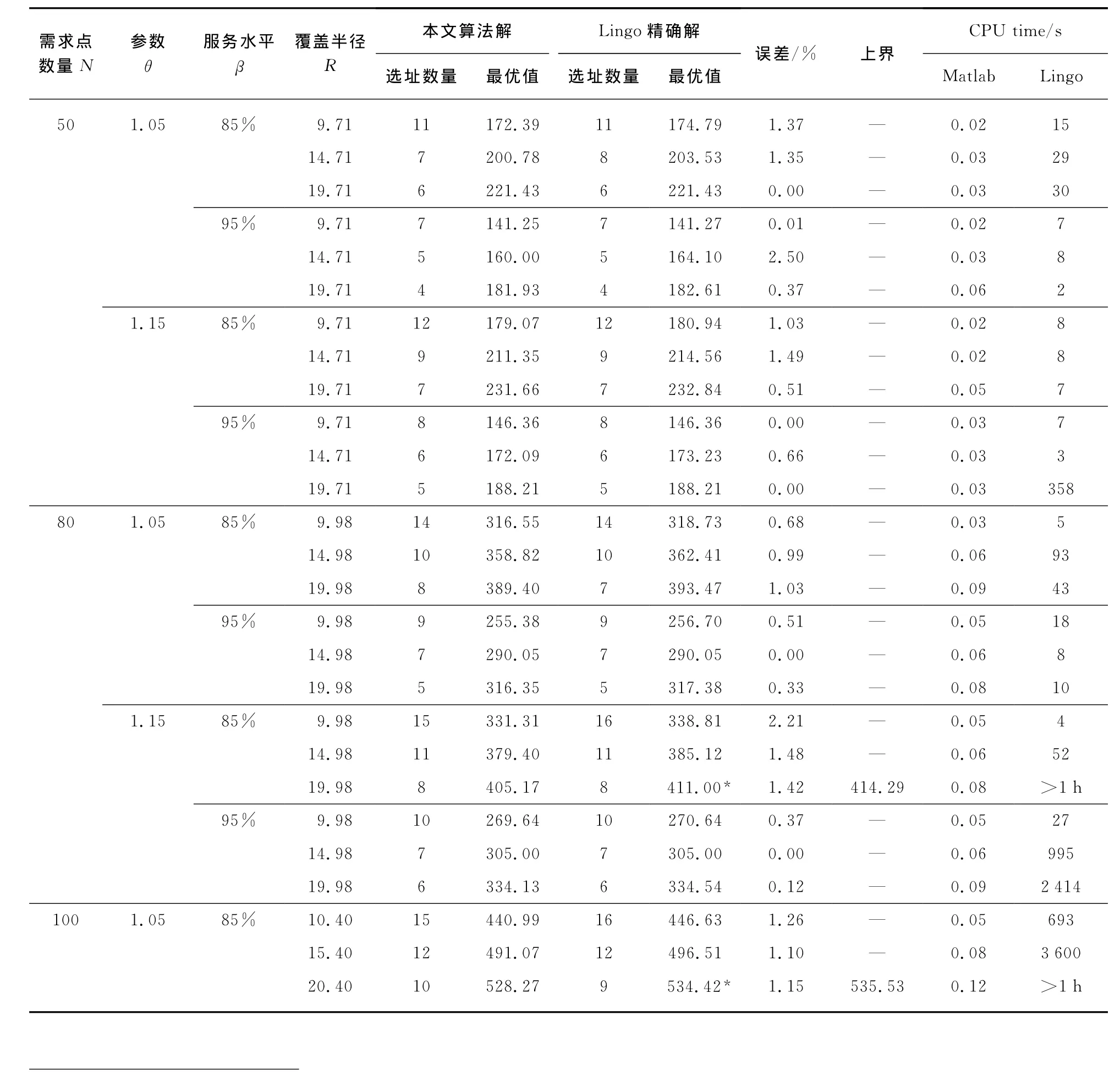
表1 计算结果Tab.1 Computational results

（续表）

由表1可以发现：在选址数量上，上述算法和Lingo程序给出的解基本一致，当覆盖半径较小时，Lingo精确解趋向于建立较多的设施点，在覆盖半径较大时，情况则恰好相反，但两者的选址数量之差最多不超过1.所以从选址数量上来看，最终结果表明：通过选择较少的设施点把服务器集中起来服务，可以得到较好的选址结果，这同性质1的结论是一致的.对同一规模的问题：当服务器的服务半径越大时，在同等条件下它所覆盖的需求也越多，同时所需建立的设施点数量也较少，这同直观感觉是一致的.

在解的质量方面，上述算法同精确解（可行解）的误差大多在3%以内，其中仅有一例除外，误差最大为3.48%.实际的计算结果表明：算法第二阶段的Server Moving部分并不总是可以进一步改进目标函数值，改进的程度大约在1%左右.但是目标函数改进却额外增加了一个新的设施点，当设施点的固定建造成本较大时，结果可能并不理想.

最后，在程序运行的时间方面，上述算法具有较大的优势.即使是在N＝120时，Matlab的求解时间也不到1s，然而通过Lingo程序求解混合整数线性规划模型M2时，在N≥100时，大部分实例运行1h以上仍然得不到最优解.所以上述算法可以迅速地对大规模问题提供合理的下界估计.

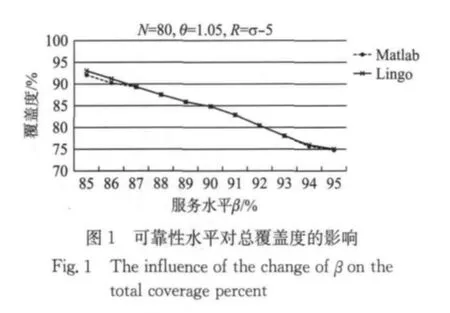
为了分析可靠性水平β对总需求量覆盖情况的影响，选择需求点数量N＝80，θ＝1.05，覆盖半径R＝组的数据，考察β在85%～95%之间变动时（每间隔1%取值），需求覆盖度（实际覆盖的需求量／总需求量×100%）的变动情况，如图1.可以发现：随着可靠性水平的不断提高，总的覆盖度逐渐减少，但是这种关系并不是严格线性的；同时，本文算法求出的最优解和Lingo给出的最优解之间的差距非常小，这也说明了上述算法的有效性，Lingo仍有3组数据在1h之内无法求得最优解（β＝88%，93%，94%）.

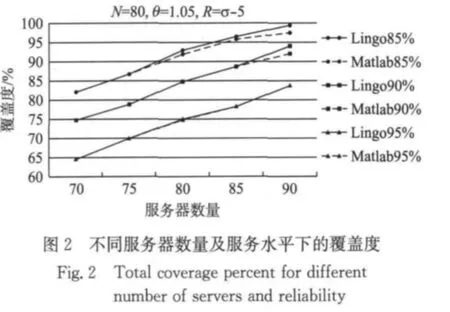
图2显示了服务器数量和服务可靠性水平对需求覆盖度的影响，其中实线标记的部分为Lingo给出的最优解，虚线部分是Matlab运行本文算法得出的解.可以发现：在同一可靠性水平时，服务器数量越多，覆盖的总需求也越多；在同一服务器数量时，可靠性水平越小，覆盖的总需求越多.总体来看，本文算法同Lingo精确解之间的差异相对较小，当服务器数量较多以及总的覆盖率较大时，误差相对增加，但最多不超过2%.

4 结 论

本文建立了有服务水平保证、基于排队论的应急服务车辆最大覆盖选址模型.由于运用了排队论模型来研究应急服务车辆的繁忙状态，因此可以不用假定各个服务器繁忙与否是相互独立的，而基于区域水平的服务器繁忙率也比系统水平的估计更准确.与以往文献不同的是，在处理服务水平约束时，它们多从机会约束的角度通过调整服务器的数量来满足约束条件，而本文则从调整覆盖量的角度给出了约束条件.模型M1提供了求解问题的描述性框架，而服务水平和排队系统中的呼叫损失率之间的相互关系使得可以将M1模型转化为较易求解的M2模型.排队论中的一个重要性质也为设计求解M2模型的算法提供了重要的依据，计算结果表明：在时间和效果上，该算法是有效的.

但是只设计了设施点服务器数量无限制时的算法，对于设施点服务器数量受到很大的限制时，性质1的优势可能不再明显.因此需求的分派方式也更接近于一般的最大覆盖问题.另外，在本文中需求可以部分满足，也没有考虑工作量平衡问题，所以对于更一般的问题还要设计相应的有效算法来求解.

［1］Toregas C，Swain R，ReVelle C，et al.The location of emergency services facilities［J］.Operations Research，1971，19：1363－1373.

［2］Current J，Morton O K.Locating emergency warning sirens［J］.Decision Sciences，1922，23：221－234.

［3］Church R，ReVelle C.The maximal covering location problem［J］.Papers of the Regional Science Association，1974，32：101－118.

［4］Daskin M S.A maximum expected covering location model：Formulation，properties and heuristic solution［J］.Transportation Science，1983，17：47－70.

［5］ReVelle C，Hogan K.A reliability－constrainted siting model with local estimates of busy factions［J］.Environment and Planning B：Planning and Design，1988，15：143－152.

［6］ReVelle C，Hogan K.The maximum availability location problem［J］.Transportation Science，1989，23（3）：192－200.

［7］Larson C R.A hypercube queuing model for facility location and redistricting in urban emergency services［J］.Computers and Operations Research，1974，1：67－95.

［8］Larson C R.Approximating the performance of urban emergency service systems［J］.Operations Research，1975，23：845－868.

［9］Marianov V，ReVelle C.The queuing probabilistic location set covering problem and some extensions［J］.Socio－Economic Planning Sciences，1994，28：167－178.

［10］Marianov V，ReVelle C.The queueing maximal availability location problem：A model for the siting of emergency vehicles［J］.European Journal of Operational Research，1996，93：110－120.

［11］Schilling D A，Jayaraman V，Barkhi R.A review of covering problem in facility location［J］.Location Science，1993，1（1）：25－55.

［12］Farahani R Z，Asgarin N，Herdari N，et al.Covering problems in facility location：A review［J］.Computers ＆Industrial Engineering，2012，62：368－407.

［13］Synder L.Facility location under uncertainty：A review［J］.IIE Transactions，2006，38：537－554.

［14］Boffey B，Galvao R，Espejo L.A review of congestion models in the location of facilities with immobile servers［J］.European Journal of Operational Research，2007，178：642－662.

［15］Berman O，Drezner Z.The multiple server location problem［J］.Journal of Operational Research Society，2007，58：91－99.

［16］Aboolian R，Berman O，Drezner Z.The multiple server center location problem［J］.Annals of Operations Research，2009，167：337－352.

［17］Baron O，Berman O，Krass D.Facility location with stochastic demand and constraints on waiting time［J］.Manufacturing Service Operation Management，2008，3：484－505.

［18］Borrás F，Pastor J.The ex－post evaluation of the minimum local reliability level：An enhanced probabilistic location set covering model［J］.Annals of Operations Research，2002，111：51－74.

［19］Narayan B U.An introduction to queueing theory－modeling and analysis in applications［M］.Berlin：Birkhauser，2007.