数控龙门镗铣床主传动系统扭转动力学分析

许昆平，严江云，彭梁锋，肖宁

(沈机集团昆明机床股份有限公司，云南昆明650203)

主传动系统是机床工作的重要组成部分。主轴箱的齿轮传动系统经常处于高速、重载的运行环境，其传动精度直接影响机床的加工精度。传动齿轮在切削过程中极易因重载、高速等原因产生较大的振动和噪声，从而导致主传动系统的某些部位受损，进而影响机床的切削精度［1-3］。因此，开展XK(H)2740数控龙门镗铣床主传动系统的动态特性分析，对于减小主传动系统的振动与噪声，优化数控龙门镗铣床主传动系统的动态性能具有重要的指导意义。

XK(H)2740数控龙门镗铣床主传动系统齿轮传动装置主要采用宽斜圆柱齿轮，设计时一般将齿轮作为刚体处理，不考虑轮齿受载后的变形，因而齿轮在动态运转过程中会出现振动大、噪声大等问题［4］。作者通过分析齿轮副接触线长度的变化，根据单位接触线的啮合刚度计算斜齿轮副的综合啮合刚度［5-6］，求解XK(H)2740数控龙门镗铣床主传动系统在刚度激励及误差激励作用下的动态响应［7-8］，并对其动力学特性进行分析，对减少系统的振动和故障提供了依据，也为系统的动态性能优化奠定了基础。

1 XK(H)2740主传动系统传动原理

图1为XK(H)2740主传动系统的传动原理图，其中轴Ⅰ为输入轴，轴Ⅳ为输出轴即铣轴。该传动系统为三级两挡斜齿轮传动，电机通过联轴器将运动输入到齿轮轴Ⅰ，齿轮轴Ⅰ通过滑移齿轮2进行换挡并将运动传递到齿轮3，齿轮3带动轴Ⅲ转动，通过轴Ⅲ上的齿轮5将运动传递到铣轴Ⅳ，进而将运动输出并进行切削。文中针对主传动系统高速挡进行扭转动力学研究。

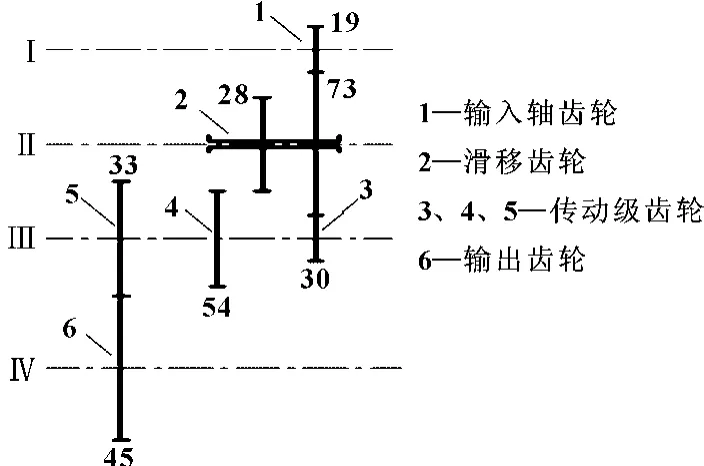
图1 XK(H)2740主传动系统传动原理

2 主传动系统扭转动力学模型

影响系统动态特性的因素主要有刚度激励、误差激励、阻尼激励以及冲击力激励，然而啮合刚度和误差激励对传动系统的动态性能影响最大，所以在建立系统的动力学模型时必须考虑各级齿轮副的啮合刚度和误差对振动的影响。利用集中参数法建立XK(H) 2740数控龙门镗铣床主传动系统的扭转振动动力学模型，如图2所示。

图中，各个传动轴的扭转刚度和阻尼分别为K1、K2、K3和C1、C2、C3，各个齿轮副的啮合刚度和阻尼分别为k1、k2、k3和c1、c2、c3，各个质量块的转动惯量分别为I1、I2、I3、I4、I5、I6和I7，各个质量块的半径分别为R1、R2、R3、R4、R5、R6和R7，输入扭矩和负载扭矩分别为Ts和Tc，三个齿轮副的综合误差分别为e1、e2、e3。

图2 主传动系统扭转动力学模型

根据图2，利用Lagrance法建立其扭转动力学方程，即:

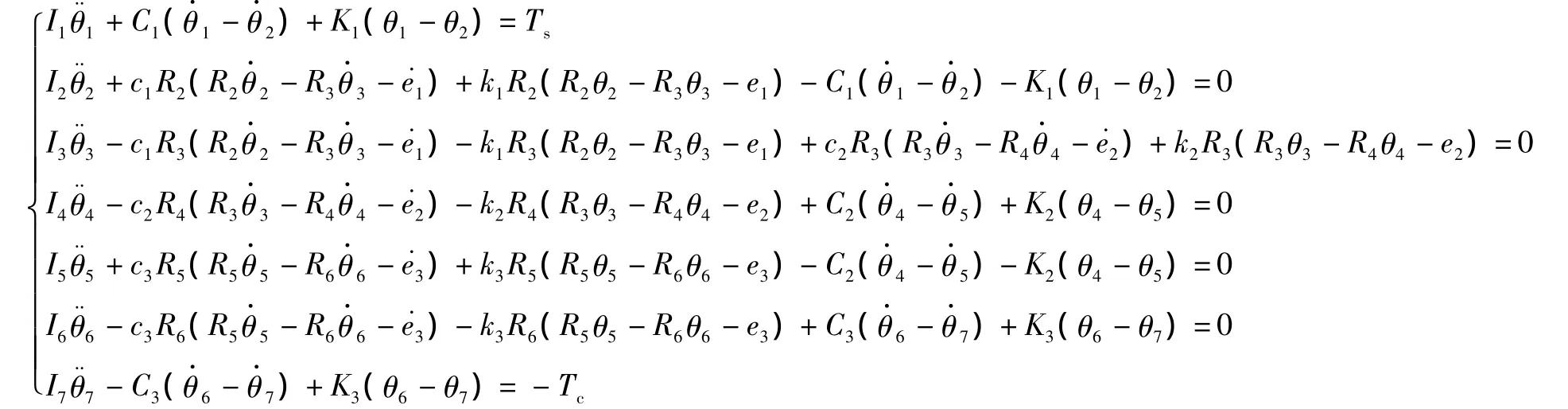
令xi=Riθi，将角位移形式的动力学方程转化为线位移形式的方程。同时令可得:

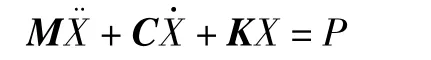
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;P为载荷向量;X为位移向量。

3 主传动系统扭转动态响应分析

3.1 刚度激励

刚度激励是齿轮啮合过程中单双齿对啮合交替出现引起的动态激励。尽管斜齿轮在啮合啮合过程中齿轮的啮合刚度不会发生突变，然而在不同的啮合位置，轮齿的啮合刚度也是不同的。

文中结合单齿单位长度的啮合刚度的定义，根据齿轮接触线的长度变化，求解主变速传动系统中斜齿轮副的时变啮合刚度。齿轮副的啮合刚度可表示为:

式中:k0为单位接触线长度的啮合刚度;

L(τ)为齿轮副瞬时总接触线长度，τ=t/Tz，Tz为啮合周期。

该齿轮副瞬时接触线总长度为:

Lm=bεα/cosβb，b为齿宽，εα为端面重合度，βb为螺旋角。

各级齿轮副啮合刚度如图3所示。

经过整理得到

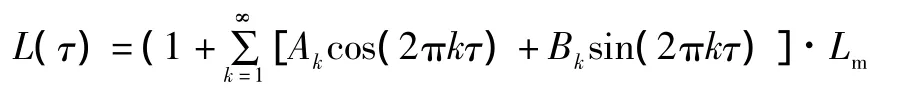
图3 各级齿轮副啮合刚度

3.2 误差激励

在进行振动分析时，齿轮的误差一般可以用实测的误差数值或误差曲线、傅里叶级数以及简谐函数来表示。实测的误差数值或误差曲线能比较真实地反映实际情况，然而在实际测试中难以实现，因此采用简谐函数来表示。在影响齿轮振动的各项误差因素中，齿距误差和齿形误差影响最大，故齿轮误差激励可表示为:

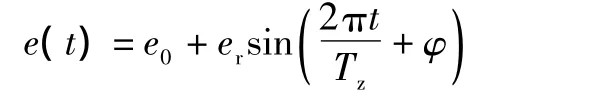
式中:e0、er分别为轮齿误差的常值和幅值;Tz为齿轮的啮合周期;φ为相位角。

齿轮的精度等级为5LM，则时变误差曲线如图4所示。

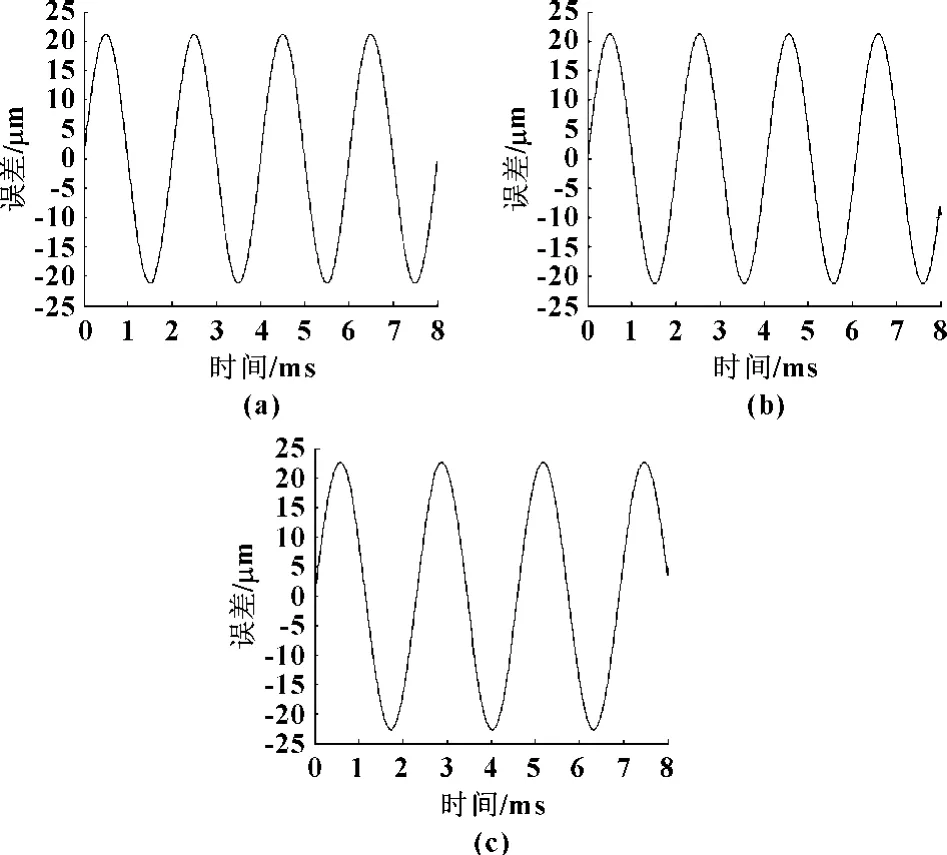
图4 各级齿轮副误差曲线

3.3 主传动系统动态特性分析

3.3.1 固有特性分析

为了减小主传动系统的振动，避免产生共振，应使齿轮啮合激励的频率远离系统的固有频率。由于系统的固有特性与外力无关，因此在求解系统固有频率时可忽略外部载荷与阻尼的影响。主传动系统无阻尼自由振动的运动方程为:

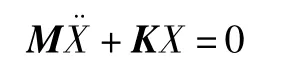
其对应的特征方程为:

式中:ωi为系统第i阶固有频率;ψi为对应的第i阶振型向量，i=1，2，…，n。

对系统的无阻尼自由振动方程进行求解可以得到系统的固有频率，如表1所示。

表1 主传动系统前10阶固有频率 Hz

该主变速传动系统输入级转速为3 445 r/min，啮合频率为490 Hz;中间级转速为2 182 r/min，啮合频率为490 Hz;输出级转速为1 600 r/min，啮合频率为435 Hz。与表1中系统前10阶固有频率进行比较，各阶啮合频率均远离系统固有频率，系统不会产生共振。

3.3.2 动态响应分析

根据建立的主传动系统扭转动力学模型，采用五阶变步长自适应Runge-Kutta法求解系统方程，计算得出位移、速度和加速度的时域响应，通过快速傅里叶变换FFT得到其频域响应。输入级齿轮副主动轮的时域和频域响应曲线如图5所示，输出级齿轮副从动齿轮的时域和频域响应曲线如图6所示。

由图5和图6可以看出:该主变速传动系统各齿轮振动位移一般为02×10-3rad，最大振动速度为2 rad/s，输出级齿轮副的振动位移较大，振动速度随齿轮的啮合速度增大而增大，振动的频率以齿轮的固有频率为主。

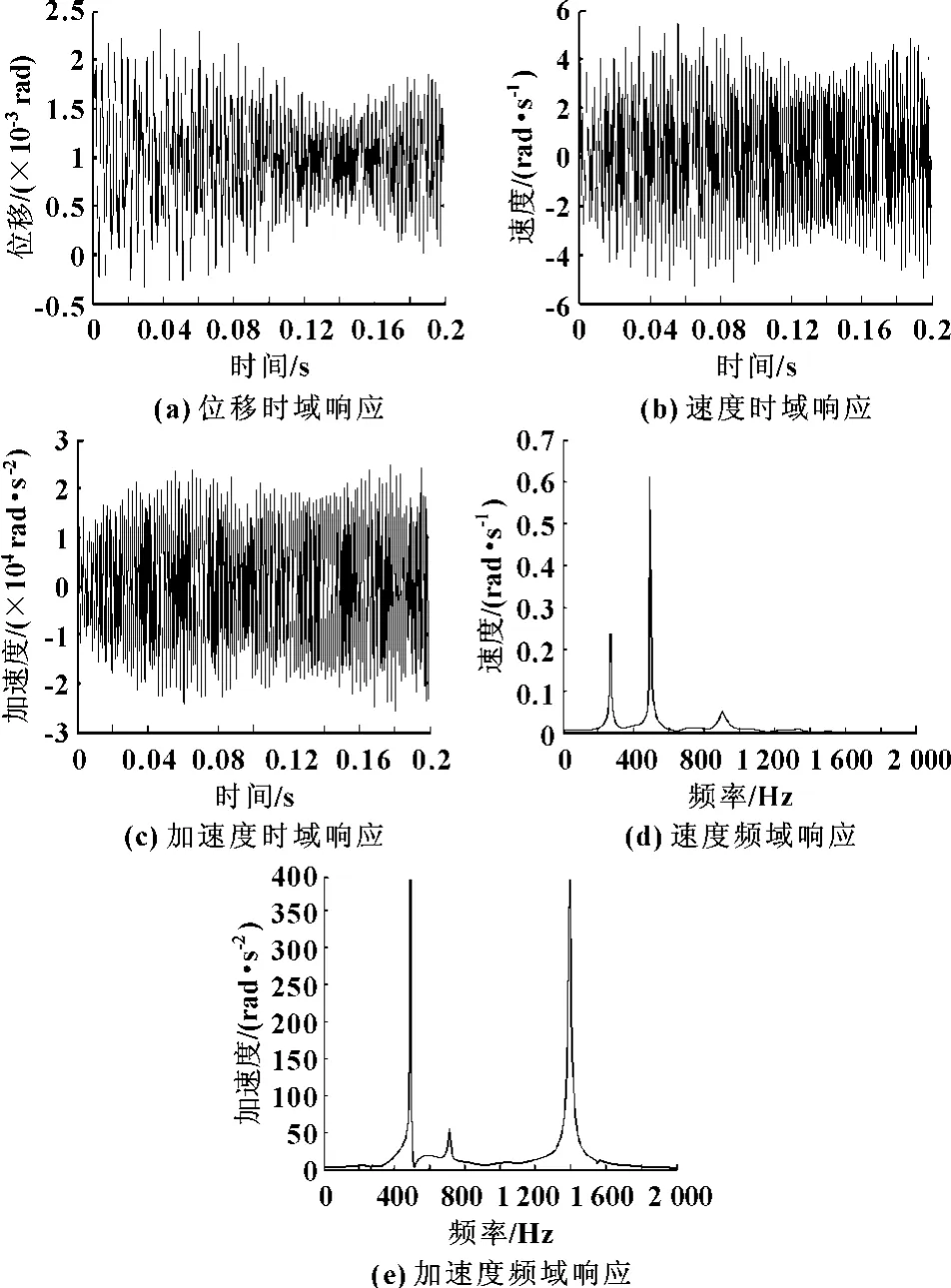
图5 输入级齿轮副主动轮的时域和频域响应曲线

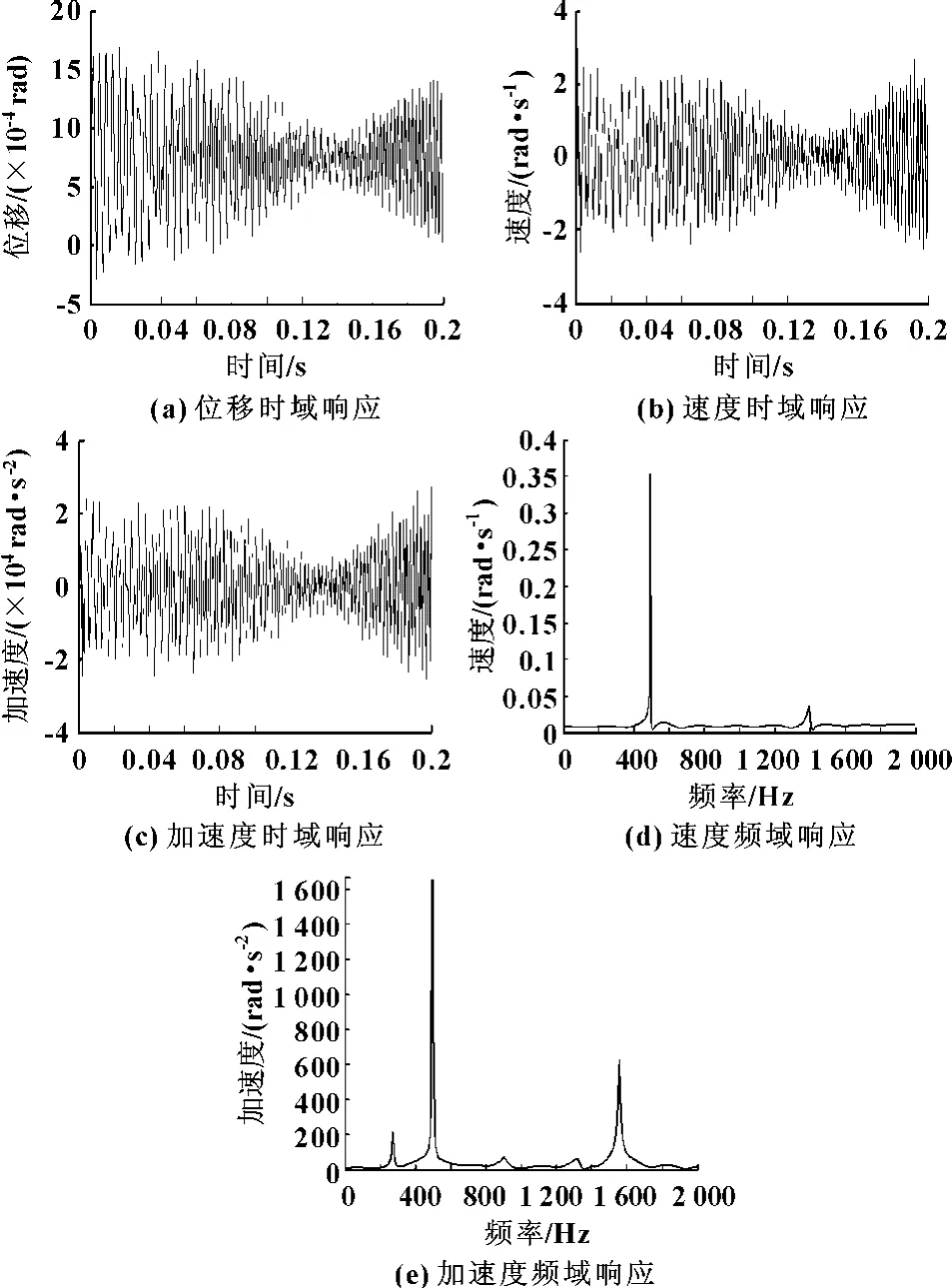
图6 输出级齿轮副从动轮的时域和频域响应曲线

4 结论

针对XK(H)2740主变速传动系统，考虑扭转振动对系统动态性能的影响，采用集中参数法建立了XK(H)2740主变速传动系统的扭转动力学模型，并利用Lagrance法建立了系统的动力学方程，得到以下结论:

(1)计算XK(H)2740数控龙门镗铣床主传动系统的固有频率，结果显示输入级和输出级齿轮副的啮合频率与系统固有频率相差较远，表明主传动系统不会产生共振现象，验证了结构设计的合理性;

(2)综合考虑齿轮接触线的变化规律以及单齿单位长度的啮合刚度，根据接触线时变长度计算了齿轮副的时变啮合刚度，该方法简便可靠，提高了计算效率;

(3)综合考虑刚度激励和误差激励对系统的影响，计算了XK(H)2740数控龙门镗铣床主传动系统的动态响应，分析判断该系统振动情况良好;

(4)文中动态响应分析为机床整机动力学研究及数值模拟奠定了基础，对减少系统的振动和故障提供了依据。

【1】李润方，王建军.齿轮系统动力学［M］.北京:科学出版社，1997:11-59.

【2】杨橚，唐恒龄，廖伯瑜.机床动力学［M］.北京:机械工业出版社1983:45-73.

【3】邰晓辉，翁泽宇，彭伟.XK717数控铣床进给系统部分连接副刚度及阻尼的参数识别［J］.浙江工业大学，2006，19(3):16-19.

【4】李瑰贤，马亮，林少芬.宽斜齿轮副啮合刚度计算及扭振特性的研究［J］.南京理工大学学报，2002，26(1):35-39.

【5】李瑰贤，马亮，陶建国，等.舰船用齿轮传动啮合刚度及动态性能研究［J］.船舶工程，2000，20(5):41-44.

【6】朱才朝，陆波，宋朝省等.大功率船用齿轮箱系统耦合非线性动态特性研究［J］.机械工程学报，2009，45(9): 31-35.

【7】THEODOSSIADES S，NATSIAVAS S.Nonlinear Dynamics of Gear Pair Systems with Periodic Stiffness and Backlash［J］.Journal of Sound and Vibration，2000，229(2):287 -310.

【8】WALHA L，FAKHFAKH T，HADDAR M.Nonlinear Dynamics of a Two-stage Gear System with Mesh Stiffness Fluctuation，Bearing Flexibility and Backlash［J］.Mechanism and Machine Theory，2009，44(5):1058-1069.