基于MATLAB的振动压路机橡胶减振器的参数优化分析

但斌斌，邬俊惠，容芷君，周鼎

(武汉科技大学冶金装备及其控制教育部重点实验室，湖北武汉430081)

压路机工作时的振动和噪声作为一种环境污染，逐渐引起了社会各界的普遍关注。随着振动压路机在生产中的广泛应用，减振和降噪也逐渐成为当前振动压路机技术发展的方向之一，越来越多的研究者着力于减振系统的试验与研发。振动和噪声不仅危害操作人员的身体健康和周围人员的生活，还严重影响压路机机器零部件的工作寿命。减振系统的理论研究与减振器的开发，具有重要的实际生产意义和社会价值。

振动压路机利用安装在振动轮中偏心激振器的高速转动产生激振力来完成对路面基础的压实工作。振动压路机的工作装置在振动压实时，一方面是振动轮对被压实材料的冲击力越大，压实效果就越好:但从另一方面讲，强烈的振动有损于机器零件的使用寿命和司机的身体健康，因此要求振动压路机的上车振动能量尽量小，这就是在振动压路机上设置减振系统的目的。

振动压路机减振性能是影响操作舒适度、噪声、压路机工作性能和机器零件使用寿命的主要因素。橡胶减振器具有良好的机械性能，加工方便，具有良好的弹性稳定性及耐日照性能，常被用来作为振动压路机减振系统的重要组成部分。相比天然橡胶，丁腈橡胶材料具有良好的耐油性和较大的损耗因子，减振效果较好，从而得到广泛应用。

长安大学刘浩亮等对振动压路机的橡胶减振的动态性能进行了研究，得到一些橡胶减振器隔振性能的主要影响因素，橡胶减振器的剪切模量和损耗因子不是静态常数，而是温度和频率的函数，并且变化很大，很复杂，强调了在减振设计中必须考虑其动态性能［1］。

1 减振系统的分析与减振性能的影响因素及其评价方法

1.1 基于二自由度的减振系统的分析

橡胶减振器的作用主要表现在对振动系统的阻尼作用。试验研究表明，橡胶减振器并不完全符合黏性阻尼的假设，更具有结构阻尼的性质，其特点是，阻力大小与振动位移成正比，方向则与速度方向相反，宜采用复刚度K*表示［2］。

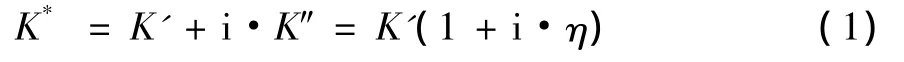
式中:K*是复刚度;

K'表示存储弹性常数 (N/m);

K″表示损耗弹性常数 (N/m)，表示与变形有90°相位差的刚度大小;

i为虚数单位;

η表示损耗系数，η=K'/K″=tanφ，φ表示同一时间内载荷超前变形的相位角。

于是根据减振器的复刚度来建立压路机的力学模型，压路机工作时一般情况下紧贴土壤表面，不会跳离地面，所以把压路机的振动系统看作是二阶系统［3-4］，如图1所示。

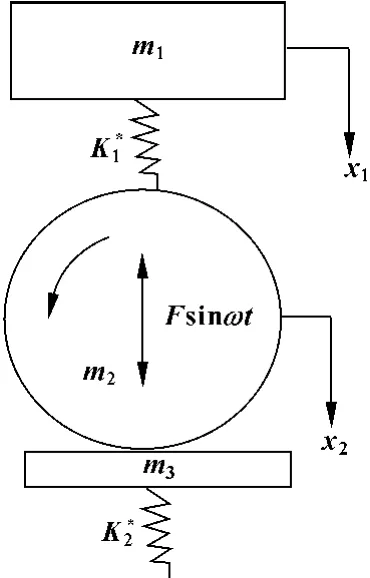
图1 压路机的力学模型

其运动学方程为:

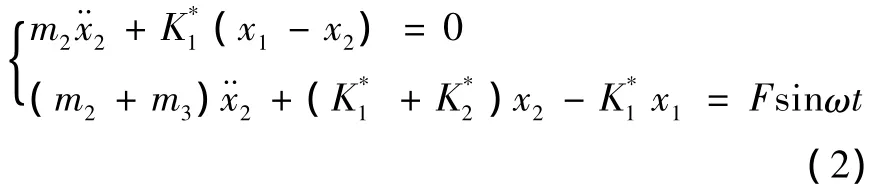
m1，m2，m3分别是上车、振动轮、随振土壤质量;

F，ω分别是激振力和激振频率;

x1，x2分别是上车和振动轮位移。

对上面第二个式子进行拉氏变换［5］，可以得到以激振力为输入、上车位移为输出的频率特性为

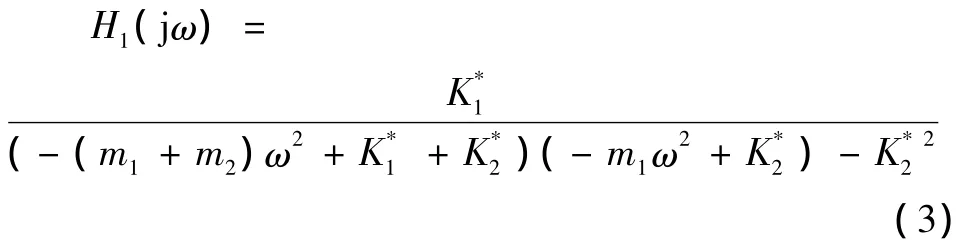
得到以激励力为输入、振动轮位移为输出的频率特性为

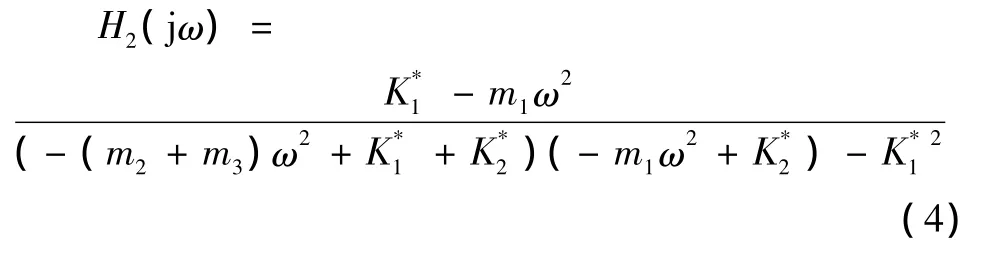
1.2 减振性能的影响因素

(1)振幅对减振性能的影响

通常情况下振动压路机的振幅指的是压路机的名义振幅，而振动压路机的工作振幅是一个变化的值，与其名义振幅和土壤的性质密切相关，希望其值在可取范围内尽量大，以保证压实的能力，但是振动轮振动过大，不但会出现过压实现象，还会导致上车的振动剧烈，严重影响驾驶舒适度。所以，振幅可能会对振动压路机减振性能产生影响。

(2)振动频率对减振性能的影响

实验和理论研究表明，机架和振动轮系统有两个共振频率。当振动频率在二阶固有频率以上时，机架的位移逐渐减小且平稳。当振动频率在二阶共振区以内时，虽然在理论上机架、振动轮的位移都很大，有利于压实，但机架很有可能与振动轮产生共振，这会导致机架振动更为急剧，严重影响减振效果。所以，振动频率不但影响振动压路机的压实效果，对振动压路机减振性能也有较大的影响。

(3)橡胶减振器的复刚度对减振性能的影响

减振器的复刚度实部对应其刚度，虚部对应其阻尼。减振器刚度对振动压路机减振性能的影响较大，振动压路机减振器的刚度过大，则起不到减振效果，上机架的振动会随振动轮振动的加剧而加剧;若振动压路机减振器刚度过小，则橡胶减振器对上机架起不到支撑的作用，会产生很大的静变形。振动压路机减振器的阻尼对压路机减振性能也有较大影响，在减振器固有频率不变的情况下，减振器的阻尼越大，减振器的传递率就越大［6］。

1.3 减振性能的评价方法

目前，对振动压路机舒适性的评价主要采用1/3倍频法、绝对传递率法和相对传递率法。

(1)1/3倍频法。即使用1/3倍频程中心频率对应的加速度值来评价压路机减振性能，将加速度频谱对应的1/3倍频带中心频率的带宽积分，从而求得1/3倍频程加速度均方根值。

(2)绝对传递率法。在主动减振系统中，绝对传递率为传到基础上的力与激振力之比，在被动减振系统中，绝对传递率为机械设备的振幅与基础振幅之比，绝对传递率表示经过减振后力或振动量的减小程度，当其值小于1时，才有减振效果，而且传递率越小越好。

(3)相对传递率法。在被动减振系统中，相对传递率定义为上车振幅与下车振幅的比值，相对传递率越小说明振动压路机的下车对上车传递的振动越少，减振的效果就越好，其值越大表现为下车传递给上车的能量越大，减振的效果就越差［7］。作者利用相对传递率法来求解下述计算模型。

2 MATLAB计算模型的简介与分析

采用从多种方案中选择最佳方案的设计方法。它以数学中的最优化理论为基础，以计算机为手段，根据设计所追求的性能目标，建立目标函数，在满足给定的各种约束条件下，寻求最优的设计方案。

目标是压实效果最优 (在最少的压实次数时，土壤获得最大的压实能量)，约束条件是减振效果较佳，设计变量主要是减振器的复刚度。

以压实功率积Q最大为目标函数，以减振支承系统复刚度K*1中的实部、虚部为优化模型设计变量。由于橡胶减振器的复刚度是随着振动频率和温度变化的，因此以振动压路机工作条件下的温度范围、频率范围和应变幅值范围内相应的减振支承系统中橡胶减振器性能变化为约束条件，调用MATLAB的优化工具箱，对减振支承系统复刚度K*1进行选择。

针对减振效果的量化，利用相对传递率法来量化减振效果，并作为一个约束条件。

根据相对传递率的定义，根据式 (2)可以求得上车和振动轮位移的比值:

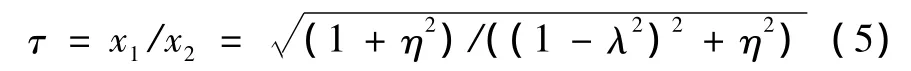
式中:λ为激振力频率与减振系统固有频率比，η表示橡胶减振器损耗系数。

当频率比λ∈ ［0，10］、η∈［0.2，0.9］时利用MATLAB计算，结果如图2所示。

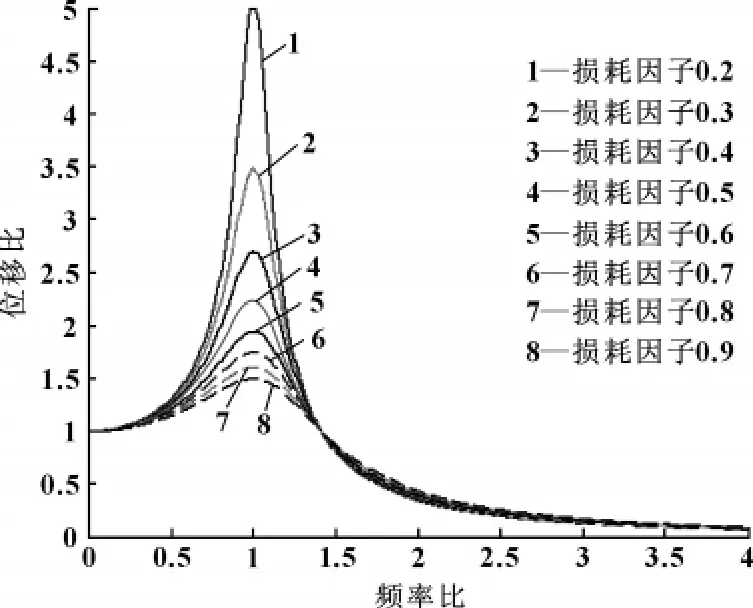
图2 不同损耗因子下频率比所对位的位移比曲线图

如图2，在不同的损耗因子条件下，可以看出:当λ≥4，传递率明显变小 (τ＜0.09)，为了减少上车振动位移，在压路机设计中一般取λ≥4，且越大越好;当λ=1时，传递率为一较大峰值，即发生共振，设计时应该避开。当橡胶减振器的振动频率在共振区附近，即λ≈1时，为了减少上车振动位移，应尽量增大损耗因子，同时橡胶减振器的复刚度的实数部分的变化会导致频率比发生变化，应尽量减少其波动。

对压实效果的量化，根据LUTHER［8］所定义的压实功率积，如下式:

压实功率积Q越大，振动轮压实能力就越大。减振效果利用传递率来量化，传递率越低越好。

根据式(4)可将式(6)变换成:

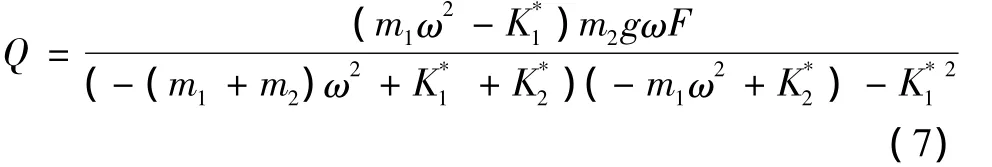
因此该计算模型可表述为:

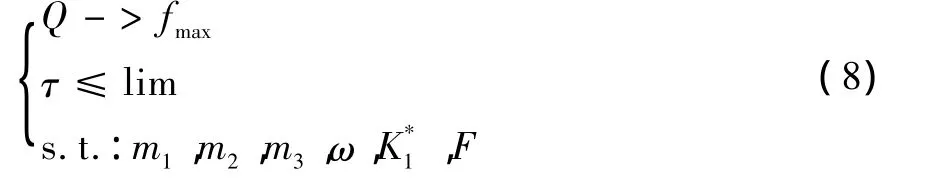
3 算例

以实验室TYZ1000型振动压路机样机为例，设计振动工作频率为25 Hz，高振幅工作时上车质量m1为1 600 kg，振动轮质量m2为3 500 kg。根据国内外文献资料，通过对振动轮土壤系统的被测性能与等效参数系统所算得的振动性能的分析比较，以10%的振动轮分配质量计入m2的数值。随振土壤质量一般为500 kg，激振力F为200 kN。

土壤的复刚度根据振动土壤密实度分成两个阶段:塑性阶段和弹-塑性阶段。高振幅作业时设塑性阶段土壤复刚度为1.65×107(1+0.80i)，弹塑性阶段复刚度为1.81×107(1+0.05i)。

结合式(1)—(7)，把传递率作为一个约束条件 (一般认为传递率小于0.000 1减振效果较好)，方程如下:的速度相当快，通过大约50次搜索就可以使误差限定在1以内;然而，再往后的搜索速度就明显变慢了许多，在这种情况下如果还采用PSO算法，那么性价比就会比较低。

图4 PSO结合Newton迭代法求解的误差曲线图

图4是采用粒子群优化算法和 Newton迭代法相结合的方式得到的误差曲线，可以看出这种算法具有很高的精度(0.001)，几乎可以满足所有的工程要求，并且速度较快。

4 结束语

重点探讨了某实用五自由度摇摆台的位置正解，采用粒子群优化算法和Newton迭代法相结合的方法，该方法利用粒子群优化算法的全局搜索能力和前期快速收敛的特点，在整个解空间里快速搜索，并且能够很快搜索到目标值附近。然而，越靠近目标值，PSO算法的收敛速度就越低，且容易陷入局部最优。所以作者在搜索后期直接摒弃了PSO算法，取而代之的是经典的Newton迭代法，这种经典的迭代法求解精度高，可以使最终的解达到理想的精度。然而，Newton迭代法也有计算量大的缺点，不过没有关系，因为在搜索前期，PSO算法已经将搜索结果锁定在目标值附近很小的范围内，所以采用Newton迭代法只要再迭代很少的几次就可以满足精度要求了。试验表明:这种改进有很高的精度和较好的实时性，对多数基于杆长驱动的摇摆台的位置正解具有借鉴意义。

【1】冯志友，李永刚，张策，等.并联机器人机构运动与动力分析研究现状及展望［J］.中国机械工程，2006，17(9): 979-984.

【2】黄真，赵永生，赵铁石.高等空间机构学［M］.北京:高等教育出版社，2006.

【3】LEE T Y，SHIM J K.Improved Dialytic Elimination Algorithm for the Forward Kinematic of the General Stewart-Gough Platform［J］.Mech Theory，2003，3(8):562-577.

【4】CODOUREY Alain.Dynamic Modeling of Parallel Robots for Computed-Torque Control Implementation［J］.The International Journal of Robotics Research，1998，17(12): 1325-1336.

【5】芮钧，陈守伦.Matlab粒子群算法工具箱求解水电站优化调度问题［J］.中国农村水利水电，2009(1):114-116.