6R机器人的联合仿真
2013-03-26黄桂武扶宇阳
杨 林,李 霆,黄桂武,扶宇阳
(1.五邑大学机电学院,广东江门 529020;2.广东科杰机械自动化有限公司,广东江门 529020)
0 引言
MATLAB软件主要是面对科学计算、可视化及交互式程序设计的环境,它的基本数据单位是矩阵。通过调用其附加的神经网络等工具箱,可使开发算法的效率比C、C++等高。机器人学的相关运算主要以矩阵运算为主,且开发机器人路径规划、逆运动学等算法时有的需要用到神经网络、遗传算法等,而这在MATLAB中的调用十分方便。而SolidWorks等三维软件可以模拟现实物理环境,通过给关节添加电机可以模拟现实环境中的电机驱动机器人关节,如果解决了Solid⁃Works引用MATLAB生成的电机数据的问题,就可以实现SolidWorks与MATLAB的联合仿真。
1 机器人联合仿真任务说明
要求机器人末端跟踪一个在30°斜面上的矩形,矩形轮廓为:500 mm×200 mm,如图1所示。
机器人初始位置设为θ2为90°,其余为0°,跟踪路径要求机器人末端从初始位置0运动到点3用PTP跟踪,再按照3-1-2-4-3顺序直线连续跟踪,再按PTP方式从位置3回到初始位置0。各段所用时间设置为2 s。
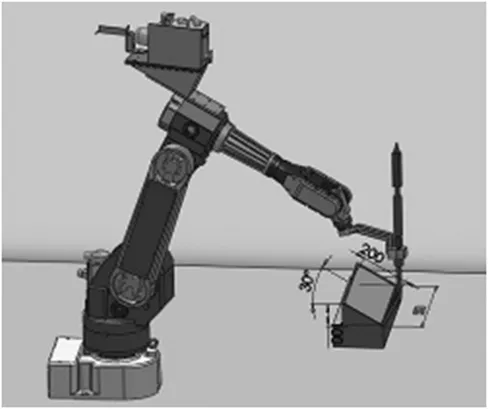
图1 任务说明

图2 跟踪路径
2 建立机器人运动学模型
2.1 建立连杆坐标系
JRB608机器人是某公司研发的一款用于搬运、焊接的6自由度机器人,末端负载能力为8 kg。各关节全部为旋转关节,其中4、5、6关节轴线相互垂直且交于一点,其几何结构满足Pieper准则。结构如图3所示。
为分析机器人运动学正逆解问题,按照Dena⁃vit-Hartenberg方法[1],结合MATLAB机器人工具箱[3]函数格式,建立如图4所示的前置坐标系,即将关节i的轴线置为第i个连杆坐标系的Zi轴,指向任意。具体建立方法为将机器人所有杆件移动到初始位置,对应所有变量均为零值。基坐标系{0}与坐标系{1}的初始位置重合,坐标系{i}的原点位于公垂线ai与关节轴i的交点处,Xi方向为沿ai方向由关节i指向关节i+1;坐标系{N}的Yi轴由右手定则确定。机器人后三个关节轴线交与一点,原点都设在交点上。对应于图4所建立的坐标系,机器人D-H参数 αi、ai、 di、 θi(i=1,2…6)如表1所示。四个参数依次表示连杆扭角、连杆长度、两连杆距离、两连杆夹角。
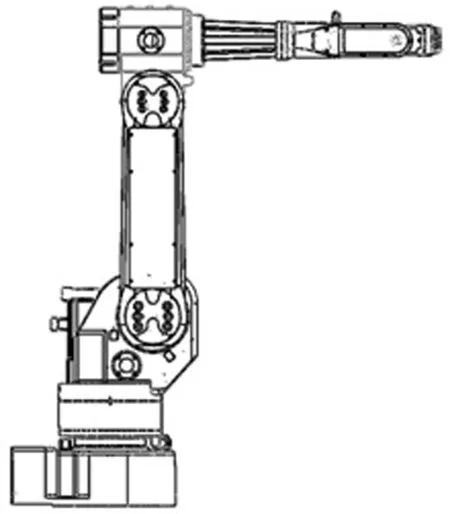
图3 JRB608结构
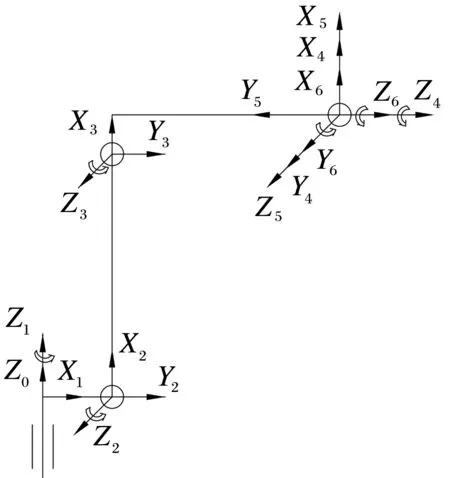
图4 机器人坐标系
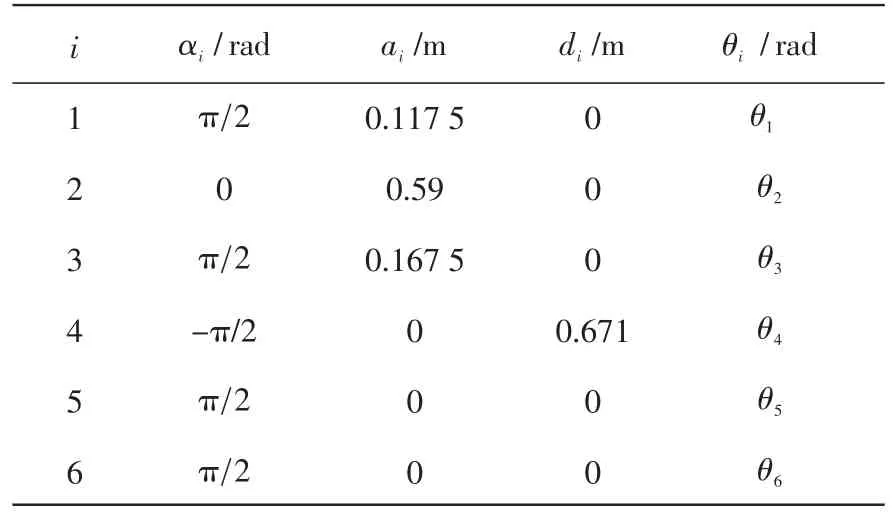
表1 JRB608机器人连杆参数
2.2 建立机器人运动学方程
2.2.1 机器人正向运动学
运动学正问题就是给定杆件的几何参数和关节的位移,求解末端连杆坐标系相对于基座标系的位姿。
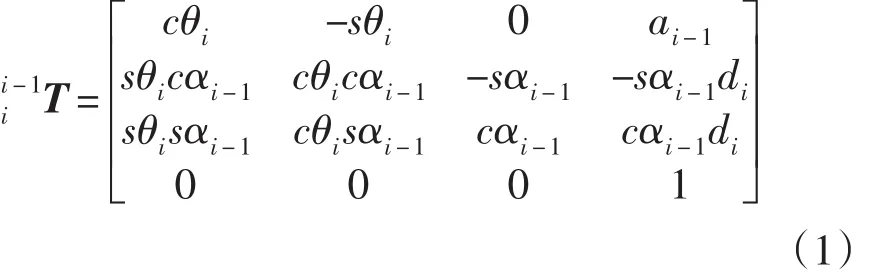
式(1)中c=cos,s=sin。代入数据可得到机器人末端相对于基座标系的位置和姿态,矩阵表示为:

式(2) 中, nx、ny、nz表示坐标系{6}的 X 轴与基坐标系{0}的 X0、Y0、Z0轴夹角的余弦值,ox、oy、oz表示坐标系{6}的 Y 轴与基坐标系{0}的X0、Y0、Z0轴夹角的余弦值, ax、ay、az表示坐标系{6}的Z轴与基坐标系{0}的 X0、Y0、Z0轴夹角的余弦值。 px、py、pz表示坐标系{6}的原点在基坐标系{0}中的位置。
2.2.2 机器人逆向运动学
机器人逆运动学问题是根据已知的末端执行器的位姿,求解各个关节的角度值。
本文采用微分变换求解逆向运动学问题[3]。将问题描述为:已知坐标系{6}相对于基坐标系{0}的微分变化时,求出各关节角度值的相应变化。
当微分运动相对于基座标系进行时,微分变换记为Δ,相对于坐标系T进行时,记为ΔT,微分变换一般表达式为[2]:
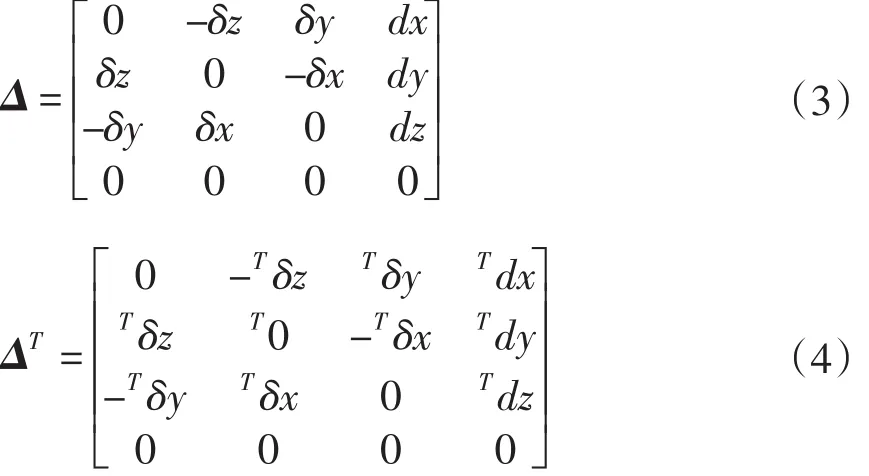
其中,δx,δy,δz分别表示dθ绕指定坐标系的X,Y,Z轴的微分旋转,dx,dy,dz表示相应的微分平移。

3 用MATLAB求关节位移
3.1 建立机器人模型
表1是结合MATLAB机器人工具箱格式得出的连杆参数,代入相关参数,得到MATLAB环境下的机器人模型。建立机器人模型过程如下:
连杆参数:
L{1}=link([pi/2.1175 0 0 0]);
L{2}=link([0.59 0 0 0]);
L{3}=link([pi/2.1675 0 0 0]);
L{4}=link([-pi/2 0 0.671 0]);
L{5}=link([pi/2 0 0 0 0]);
L{6}=link([0 0 0 0 0]);
构建机器人:
JRB_608=robot(L,'JRB608');
JRB_608.name='JRB608';
模型可视化:
theta=[0 pi/2 0 0 0 0];
plot(JRB_608,theta);
drivebot(JRB_608);
图5是根据连杆参数绘制出的连杆模型,图6为滑块控制图,可以驱动模型并查看各关节角度范围限制。
自编check.m函数用于检测所给角度是否超出角度限制,关键语句为:

图5 JRB608模型
theta(i)<min(L{i}.qlim)|theta(i)>max(L{i}.qlim)error(''):%引号内为错误提示内容。
3.2 获取各示教点位姿
SolidWorks环境下,使焊枪末端与点3重合,且使焊枪与焊接平面垂直,依次与点1、点2、点4重合,初始点为0,得出4种位姿下各关节的角度:
q0=[0 90 0 0 0 0]*pi/180;%起始点位置
q3=[-10.33 71.17-7.69-5.15-42 0]*pi/180;
q1=[-11.5 88.83-19.56-5.79-47 0]*pi/180;
q2=[11.5 88.65-17.9 5.8-47.4 0]*pi/180;
q4=[10.1 71.16-7.68 5-42.1 0]*pi/180;
机器人在点0、3时的位姿矩阵,运用MAT⁃LAB机器人工具箱函数fkine()求解:
T0=fkine(JRB_608,q0);%点0位姿矩阵
T3=fkine(JRB_608,q3);%点3位姿矩阵
机器人在点1,2,4处的位姿矩阵通过平移变换得到:
T1=transl(-0.165,0,0.095)*T3;%点1处位姿矩阵
T2=transl(0,0.49,0)*T1;%点2处位姿矩阵
T4=transl(.165,0,-0.095)*T2;%点4处位姿矩阵

图6 滑块控制图
3.3 求解关节位移
由于所给任务为在笛卡尔空间的直线运动,必须将笛卡尔空间转换到关节空间以得到关节位移增量。MATLAB中ctraj()函数可以计算两点间笛卡尔空间轨迹插补的函数。求解关节角度语句如下:
t1=0:0.02:2;%0~2s,采样时间20ms
Q0_3=ctraj(T0,T3,length(t1));%点0到点3
Q03=ikine(JRB_608,Q0_3,q0);
%点0到3各时刻关节角位移,起始位置q0
同理,可得到Q31(点3到点1)、Q12(点1到点2)、Q24(点2到点4)、Q43(点4到点3)、Q30(点3到点0)。
程序运行出来的数据就是6个关节在每个时刻的角度值,可使用语句:plot(JRB_608,Q04)在MATLAB环境下动态仿真,以检查结果的正确性。

图7 定义关节马达

图8 装载数据
3.4 生成txt文件
对于6自由度机器人,要完成末端执行器在笛卡尔空间直线轨迹仿真,想简单的靠给电机输入数据点,工作量非常大,而且一旦数据更改,就得重新输入,费时且费力。但是MATLAB能够生成txt、dat、mat等格式的文件,而SolidWorks motion可以读取txt文件格式的数据给电机,这给验证运动学算法和机器人仿真带来很大方便。
MATLAB生成txt文件语句为:
save('d:JRB6J1zhou.txt','J1','-ascii');
语句中,J1代表要写入数据,J1zhou.txt为要生成的文件名。
4 SolidWorks Motion运动仿真
4.1 SolidWorks Motion功能说明
SolidWorks Motion是集成于SolidWorks premi⁃um中的运动学与动力学分析插件,还可以检测运动过程中是否会发生干涉。使用motion分析,软件按照用户定义的装配关系,精确模拟并分析装配体的运动,以图形、动画、表格等多种方式输出分析结果。由于SolidWorks Motion运动算例分析同时计及了运动约束、材料属性、质量、及零部件接触,所以可以很方便地模拟和求解现实受力情况。
4.2 文件导入与仿真
首先在SolidWorks环境下建立好机器人模型,定义好装配关系,进入运动算例界面,按照2.1节所建立的连杆坐标系给每个关节定义电机,电机方向如图7所示,再点击“从文件装载”,如图8所示,给马达选择3.4节生成的相应txt文件,点击“计算运动算例”,就可以使机器人按照编写的算法运动。
4.3 结果分析
干涉检查。本文在环境中放置一个干涉零件,如图9所示的矩形零件,以说明焊枪与环境干涉检查方法。在Motion Manager设计树栏右键单击“检查干涉”,弹出图10所示对话框,选中要检查干涉的零部件,图10中“结束帧数”选项按照motion分析中的每秒帧数设置,本算例中每秒帧数时42,为检查前1.5 s内有无干涉出现,结束帧数应该为63。计算出的干涉显示在文本框中,点击干涉,干涉区域会着重显示,并且干涉位置会跟随帧数变化,且干涉区域可以放大以更清楚查看。根据干涉结果,可以对机器人路径规划算法进行检验,在三维实体模型下查看是否机器人已经避开环境中的障碍。
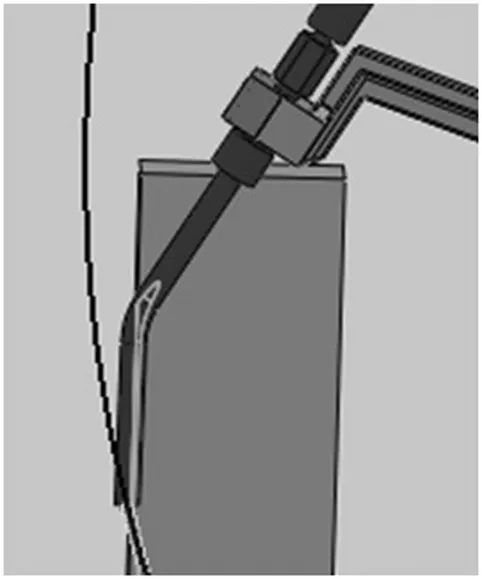
图9 干涉零件

图10 干涉检查
轨迹与速度曲线跟踪。在Motion界面,单击“结果和图解”,能生成运动过程中的关节力矩、目标点运动速度、加速度、角位移,还能对目标点进行跟踪。本文根据生成的文件,运行后对焊枪末端进行轨迹跟踪,跟踪结果如图11所示。
从图11说明此算法可以完成轨迹跟踪要求,但图12表明,末端速度有跳变,对机械结构会产生冲击,在轨迹规划阶段还需要对算法进行优化。从而为后期软件规划指明方向。

图11 末端轨迹

图12 末端运行速度
5 结语
本文通过SolidWorks与MATLAB之间文件共享,实现了两者之间的联合仿真。SolidWorks能将现实生活中的物理环境简单而又逼真地显示出来,而软件开发工作人员又正好缺少这样一个检验环境,通过观察仿真得出的曲线,软件开发人员可以直观看出已经实现了哪些功能,所编程序在实际运行中会不会产生干涉,还需要在哪些地方进行改进等;而对于机器人结构设计人员,还可以在添加了Simulation之后,机器人本体结构变形情况也会显示在仿真当中,可直观看出在完成该任务下各个零件的变形情况,从而指导结构优化设计。
综上所述,通过联合仿真,将软件开发工作者与结构设计工作者联系起来,使得在开发阶段可以得到各自想要的数据,从而为后续结构设计和软件设计工作人员提供改进方向。
[1]John J.Craig.机械人学导论[M].北京:机械工业出版社,2006.
[2]蔡自兴.机械人学[M].北京:清华大学出版,2000.
[3] Corke P I.A Robotics Toolbox for MATLAB [J].IEEE Robotics and Automation Magazine, 1996, 3 (1):24-32.
[4]张爱红,张秋菊.机器人示教编程方法[J].组合机床与自动化加工技术,2005,27(2):75-78.
[5] YUN Xiao-ping,ERIC R B.Design,Implementation,and Experimental Results of a Quaternion-Based Kalman Filter for Human Body Motion Tracking [J].IEEE Transaction on Robotics and Automation, 2004, 20(1): 160-167.
[6] A.Gasparetto,V.Zanotto.A new method for smooth tra⁃jectory planning of robot manipulators [J].Mecha⁃nism,2004,42:455-471.
[7]熊震宇,陈焕明,葛杨.基于ADAMS的弧焊机器人运动仿真[J].计算机工程与应用,2005,11:166-167,213.
[8]孔凡斌,姜培刚,宋玲玲.基于UGOpenC的FANUCM-16iB/20工业机器人动态仿真[J].计算机应用与软件,2008,25(6):169-171.
[9]王岚,陆露.套装式助力机器人动力学建模与仿真[J].机电工程,2011(03):324-328.
[10]刘成良,张为公,翟羽健,等.RV12L6R焊接机器人运动学及计算机仿真系统研究[J].机器人,1998,20(05):333-341.
