一种适用于风电并网系统的多指标加权电压稳定快速判别指标

林相彬，徐建源，黄 旭，刘劲松，张 涛

(1．辽宁省电网安全运行与监测重点实验室 (沈阳工业大学)，辽宁 沈阳 110870;2．辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006)

随着风力发电规模的不断扩大，其自身不稳定、易波动的特点对电网电压造成的诸多负面影响也愈加明显［1－5］。因此，开展适用于风电并网系统电压稳定判别方法的研究十分必要。

电压稳定性研究的重点是电压崩溃的发生机理和电压稳定性指标的确立，电压稳定性指标确立的目的是为调度运行人员提供电压稳定性参考信息，通过调度避免电压崩溃事故［6－8］。通常电压稳定研究是从其静态特性出发建立相应的指标，确定目前系统状态的电压稳定裕度［9－11］，但仅局限于对静态电压稳定机理的讨论是不够的，因此，提出了一种适用于风电并网系统的基于多指标加权的最优幂值电压稳定指标。

首先推导了Jacobian矩阵相互条件数估计指标与Jacobian矩阵解耦化为对角阵后的灵敏度逆阵元素判定指标，然后将二者相结合，通过自编程序求解最优幂值n1、n2，在此基础上提出了基于多指标加权的最优幂函数均值法。最后将指标应用于含风电场的电力系统中，并将该指标与常规裕度指标的仿真结果进行对比。通过比较可见，最优幂函数均值法的计算误差较小，且具有较宽的线性度，更适用于含风场的系统进行电压预测。

1 电压稳定判定指标推导

1.1 基于Jacobian矩阵相互条件数估计的判定指标

式中，SVD是奇异值分解计算。

用式 (2)计算矩阵条件数和最小奇异值的速度很慢。对一个n×n的矩阵，必须要计算n3次，该方法虽然很准确但无法应用于系统的在线计算。为了能快速估计矩阵条件数，通过计算雅可比矩阵的1阶范数和无穷范数得到矩阵J的模，并通过迭代算法来估计J－1的模。该方法对一个n×n矩阵进行矩阵条件数估计需要计算n2次，比奇异值分解计算快很多，同时矩阵条件数估计指标在奇异点附近有良好的线性行为。

1.2 基于Jacobian矩阵解耦的电压稳定判定指标

通过求解雅可比矩阵的逆阵可得到因控制向量和扰动向量的变化引起的状态向量的变化量，进而反映节点电压稳定运行状况。但对于Jacobian矩阵的求解，以往主要通过设定电气量的初值，反复迭代计算不断修正的方法，计算时间长且实时性差，不能实现在线求解。利用同步向量测量数据代入潮流方程，可得到精确的电网Jacobian矩阵，将潮流方程进行解耦，求解出Jacobian逆矩阵对角化元素值，并根据对角化元素值提出电压稳定判定指标。

电力系统中的微分代数方程表示如下:

电力系统正常运行时，潮流Jacobian矩阵非奇异，是一个可逆的满秩矩阵，当系统运行在电压崩溃临界状态的鞍结分岔点时，对应的潮流雅可比矩阵奇异。因此，潮流Jacobian矩阵的状态能很好地反映出节点电压稳定运行状况。确定奇异矩阵的方法是计算当主矩阵中元素发生变化时其逆矩阵的灵敏性。本文采用求解矩阵条件数的方法判断雅可比逆阵的灵敏性。矩阵的条件数T由式 (1)得到:

式中，‖J－1‖P是雅可比矩阵J的P阶范数，P等于1、2或无穷。如果 P=2，条件数由式 (2)计算:

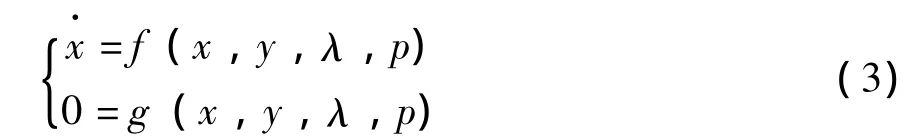
式中，x∈Rn是系统状态变量向量，y∈Rm是系统代数变量向量，λ∈Rl是一组不可控的参数，p∈Rk是一组可控的参数，f(x，y，λ，p)是系统参数动态行为的一个向量函数，g(x，y，λ，p)是潮流等式的一个向量函数。在小信号稳定性分析中，电力系统状态方程在工作点附近必须被线性化。将式 (3)线性化得到式 (4):

为得到第i个节点有功功率不平衡量，ΔPi的变化只引起各节点电压相位角θ的变化，不引起电压V大小的变化，无功功率不平衡量ΔQi的变化只引起各节点电压大小的变化，不引起其相位角的变化，采用雅可比矩阵求逆解耦方法如下式:

随着节点负荷的增加，潮流雅可比灵敏度矩阵对角化元素的值逐渐增大，当临近电压崩溃点时，这一值增大得非常快。潮流雅可比矩阵元素值能很好地反映出对应节点的性质。因此，在潮流雅可比矩阵的基础上计算电压稳定指标是可行的。因此，利用从空载到某一特定负荷，∂θi/∂Pi和∂Vi/∂Qi值产生的偏移量作为负荷节点i的电压稳定性指标。按照这一准则可得到以下2种电压稳定性指标:

这2个指标分别反映出节点崩溃是有功传输越过极限引起还是无功缺损造成。节点电压即将出现电压崩溃时，潮流雅可比矩阵奇异，此时IPi和IQi趋于0。

2 最优幂函数均值电压稳定判定指标

传统的电压指标只在电压崩溃点附近小范围内有线性行为，在这个小范围内 (重负荷时)能准确预测电压崩溃的发生，而在轻负荷时，指标没有线性行为，且每个指标相对于理想线性指标都有不同程度偏离。为更准确地进行预测，减小这种偏离是很重要的。基于Jacobian矩阵相互条件数估计的电压稳定判别指标具有较快的计算速度，基于Jacobian矩阵解耦的电压稳定判定指标具有较高的准确度，且能反映出节点崩溃是有功传输越过极限引起还是无功缺损造成。根据2种判定方法，结合指标原理特性，推导一种能扩展指标线性行为的最优幂函数均值判别指标，它具有2种判定方法的优点，且有较宽的线性度，使负荷在更广范围内变化时对电压稳定准确预测成为可能。

在进行幂函数均值计算时，用到的单位值是以每个指标的最大值作为基值。在这种情况下，可以用下式得到指标的最优幂函数均值的判定指标:

综合判定指标，f(λ)的幂值n1、n2的初值可由I(λ)的二阶导数确定:

通过迭代和修正幂值变量，当满足式 (10)时得到最优幂值n1、n2。

由式 (8)得到的平均指标预测电压稳定产生的误差比单独一个指标I(λ)产生的最大误差小，并由式 (10)可见，该指标具有良好的线性度。该方法解决了不完全线性指标只在重负荷附近有线性行为及引起的电压稳定预测误差较大甚至错误的问题。

3 算例分析

3.1 EPRI－36节点仿真算例

首先利用电网电压稳定判定方法对EPRI－36节点系统进行计算，系统中发电厂总装机容量为2 645 MW，在33节点处接入容量为500 MW的风电场。

由于电力网络中的大停电事故通常是由局部节点故障逐渐发展扩大而形成的，且在事故发生和发展过程中与薄弱节点和薄弱区域有密切关系，因此，算例中选取系统电压稳定薄弱节点9和23作为研究对象。设网络初始负荷为S0，各母线负荷为Si，分别在全网负荷按照λ速率增长，节点9、节点23负荷按λ速率增长，2种负荷变化情况下，利用常规的电压稳定裕度判定方法和对选取节点电压稳定性进行估计，结果如表1所示。

由表1可见，当系统以不同负荷模式增加时，应用常规电压裕度判定指标对电网电压稳定性预测的误差在3%～7%，运用最优幂函数均值指标对电网电压稳定预测时，误差小于3%，可得到更精确的预测结果。

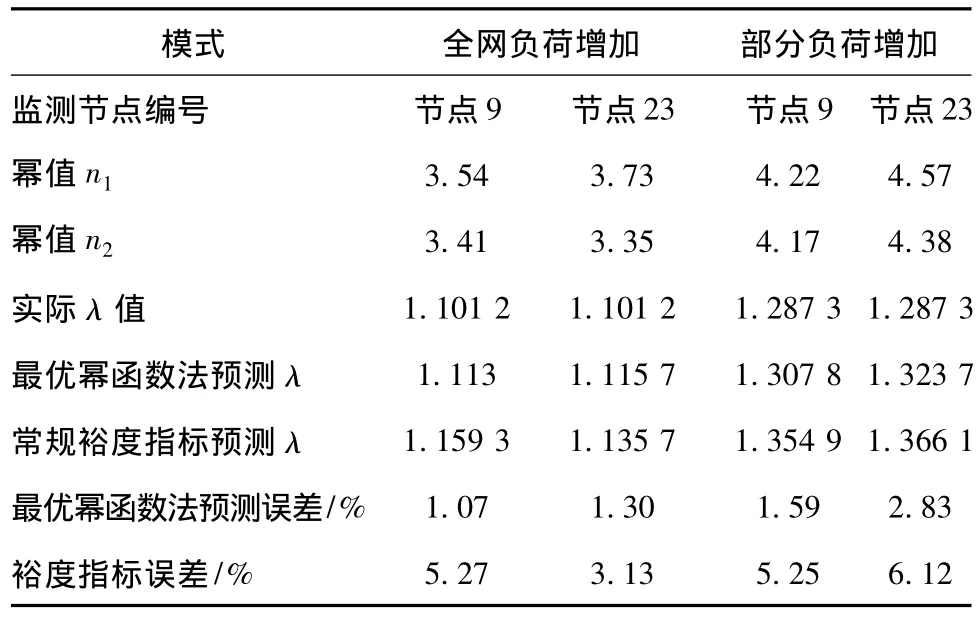
表1 常规裕度判定方法和最优幂函数均值判定指标预测对比

3.2 区域电网仿真算例

选取某区域电网为研究对象，应用最优幂函数均值判定指标对该电网电压稳定性进行判定和预测，节点编号和系统结构图如图1所示。其中节点1为松弛节点，节点6为风场接入点，风机为双馈风力发电机，负荷区域Ⅰ为上述综合动态模型，负荷区域Ⅱ和Ⅲ采用恒功率负荷形式。

图1 东北区域电网结构图

设初始负荷为S0，所有母线负荷都以相同速率λ增加。因此，i号母线上的负荷为Si=Sio×λ。通过编程计算得到Jacobian矩阵相互条件数指标、IPi和IQi指标及最优幂函数均值的判定指标。系统电压稳定性判定结果如图2所示。

由图4(a)可见，随着系统负荷不断增加，Jacobian矩阵相互条件数不断下降，在系统电压将要发生崩溃时接近于0，表明系统Jacobian矩阵临近奇异，该指标可准确地反映系统当前的运行状态，但在重负荷下不具有线性行为，因此给系统预测带来困难。当指标IPi和IQi趋于0时，潮流雅可比矩阵奇异，节点电压即将出现电压崩溃，由图4(a)可大致推断出，当电网负荷因子λ继续增大时，节点3的值将最先减小到电压崩溃时的极限值，因此，电网电压的崩溃是由于节点3的无功缺额而导致。由图4(b)中的综合指标可见，I1(λ)和I2(λ)与理想线性指标都有一定的偏差，但通过式 (8)计算得到的最优幂均值曲线的线性区域有很大增加。

图2 各指标对电压稳定性的判定曲线

计算过程中选取薄弱节点3～节点7作为研究对象，计算结果如表2所示。

表2 最优幂函数均值判定指标对电网电压稳定的预测

由表2可见，最优幂函数均值判定指标对负荷节点电压稳定预测的误差小于2%。该方法具有计算简单准确、线性度宽的特点，因此，对于系统在轻负荷下的电压稳定性也具有较好的指导作用。

4 结论

a． 推导了Jacobian矩阵相互条件数电压稳定指标与潮流Jacobian阵解耦求取灵敏度逆矩阵对角化元素的电压稳定指标，将两者相结合，提出了最优幂函数均值法，在预测含风电系统电压稳定性时，误差小于3%。

b． 最优幂函数均值判定指标能够通过IPi=明确区分节点崩溃是有功传输越过极限引起，还是无功缺损造成的，能够定量地为调度人员提供有功和无功的控制量，从而作为电压稳定控制的参考依据。

c． 最优幂函数均值判定指标与常规裕度指标相比具有更宽的线性行为，克服了大多数常规电压指标只在电压崩溃点附近小范围内有线性行为的缺点，为负荷大范围发生变化时对电网电压稳定性进行预测提供了可能。

［1］ 汤 宏，吴俊玲，周双喜．包含风电场电力系统的小干扰稳定分析建模和仿真 ［J］．电网技术，2004，28(1):38－41．

［2］ 张红光，张粒子，陈树勇，等．大容量风电场对电力系统小干扰稳定和阻尼特性的影响 ［J］．电网技术，2007，31(13):75－80．

［3］ 金 鑫．风力发电机组系统建模与仿真研究［D］．重庆:重庆大学，2007．

［4］ 高一丹，张步涵．并网双馈风力发电机组的建模与仿真［J］．湖北工业大学学报，2010，25(1):75－80．

［5］ 迟永宁，王伟胜，刘燕华．大型风电场对电力系统暂态稳定性的影响 ［J］．电力系统自动化，2006，30(15):10－14．

［6］ 徐建源，杨红磊，齐伟夫．区域电网相量测量单元的配置方案及变电站动态电压稳定性的模拟评估［J］．电网技术，2008，23(3):79－83．

［7］ J．A．Nelder and R．Mead， “A simplex method for function minimiaztion，”The Comput．J．，vol．7，no．4，pp．308 －313，1965．

［8］ N．Dobigeon，S．Moussaoui，M．Coulon，J．-Y．Toumeret，and A．O．Hero，“Joint Bayesian endmember extraction and linear unmixing for hyperspectral imagery，”IEEE Trans．Signal Processing，vol．57，no．11，pp．4 355 －4 368，Nov．2009．

［9］ A．M．Gole，S．Filiadeh，R．W．Menzies，and P．L．Wilson， “Optimization-enabled electromagnetic transient simulation，”IEEE Trans．Power Del，vol．20， no．1，pp．512 － 518，Jan．2005．

［10］ 周双喜，姜 勇，朱凌志．电力系统电压静态稳定性指标述评 ［J］．电网技术，2001，25(1):1－7．

［11］ 孙华东．计及感应电动机负荷的电力系统在线电压稳定指标［D］．北京:中国电力科学研究院，2005．