双馈风机并网仿真模型的改进研究
2013-03-25吴冠男徐建源
吴冠男,徐建源,黄 旭,朱 钰,孙 峰
(1.辽宁省电网安全运行与监测重点实验室 (沈阳工业大学),辽宁 沈阳 110870;2.辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006)
双馈型风力发电机 (DFIG)由于效率高及变频装置容量小等诸多的优势,已成为当前主流的风机机型[1-3]。在双馈型风力发电机并网及其影响的相关仿真计算中,建立能够准确反映双馈型风力发电机实际输出特性的风机模型是十分重要的[4]。
关于双馈型风力发电机及其控制系统的数值仿真模型,国内外做了大量研究[5-9]。文献 [10]推导了变速恒频风电机组动态数学模型,并计算了由变流器最大电流限制的风电机组有功功率和无功功率的运行区域;文献 [11]搭建了双馈型风力发电机的矢量控制系统和考虑联结柔性的轴系模型,分析了双馈风机的功角暂态特性;文献 [12,13]详细分析了双馈型风力发电机在电网电压跌落过程中的输出特性。
本文利用拉格朗日插值法对双馈型风机并网点的实测数据进行处理,获得实际运行中双馈风机功率输出特性曲线,根据特性曲线改进双馈风机模型的有功与无功关系函数。对50 MVA双馈型风电场并入电网的仿真计算表明,应用改进模型在短路故障和负荷投切计算中,负荷投切操作的母线节点电压幅值在恢复的过程中波动相对较大,而进行短路故障节点频率和功角变化较为明显,双馈风机仿真模型对风机输出特性描述的准确性会对双馈型风电场并入电网的暂态计算结果有较大影响。
1 实测特性曲线拟合
风机输出功率的获得主要是通过测量风机端口电压、电流值来完成。电压、电流的模拟信号经过一定频率的采样和模数转换后,得到一系列离散数列,送入数字处理芯片计算,得到的结果能够完整地体现模拟量的特征。根据离散数字信号处理理论,经离散变换后,在一个周期内进行N次采样得到电压离散值序列u(n)和电流离散值序列i(n),即可求出电压的有效值Urms、电流的有效值Irms和有功功率P,其离散表达式分别为


至此,有功功率和无功功率都能顺利得出[14]。取得实测的有功功率和无功功率后,需要对其进行数据拟合,得到两者的函数关系式,即实际运行中风机功率输出特性的数学模型,从而为调整控制模型,改进双馈风机模型做准备。
本文采用拉格朗日插值法进行数据处理,其具有作为经验曲线的近似公式,在密集性插值计算中,具有速度快、计算方法简单、误差较小、便于在计算机中实现等优点。其主要方法是通过测量或试验得到在某区间上的一系列点的函数值yi=f(xi)(i=0,1,2,…,n)。根据给定的函数表构造一个既能反映函数f(x)的特性,又便于计算的简单函数p(x)来近似f(x),并使得p(xi)=f(xi)(i=0,1,2,…,n)。
为了通过拟合实测数据得到明确的函数关系表达式,可以通过n+1个不同的已知点 [xi,yi=f(xi)]来构造一个次数为 n的代数多项式 P(x)。类似抛物插值,先构造一个特殊的n次多项式li(x),使li(x)在各节点xi上满足lk(x0)=…=lk(xk-1)=0,lk(xk)=1,lk(xk+1)= … =lk(xn)=0,因为 x,x1,…,xk-1,xk+1,…,xn都是 n次lk(x)的零点,故可设:
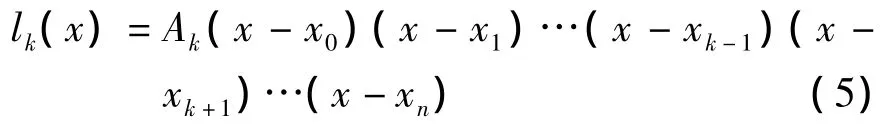
其中Ak为待定常数,由条件lk(xk)=1可求得:

代入式 (5)得

式中,lk(x)称为关于基点xi的n次插值基函数。事实上,由于每个插值基函数lk(x)都是n次多项式,它们的线性组合P(x)=称为n次拉格朗日插值多项式,并记做Ln(x)[15]。通过上述数据处理方法可以得到无功功率和有功功率的函数关系曲线,由该曲线即可得到风机端口的输出特性函数。
2 改进模型
双馈型风力发电系统包括以下几个模块:风轮机、双馈型风力发电机、网侧变流器、机侧变流器、变流器控制系统、桨距角控制系统。其结构示意图如图1所示。其中,网侧变流器及其控制系统作为双馈风机模型的主要组成部分,其功能之一是调节风机并网点无功功率输出,通过改进网侧变流器控制模型即可调整风机功率输出特性。

图1 双馈型风电系统
2.1 网侧变流器数学模型
网侧变流器采用三相电压型PWM整流器,主电路拓扑结构如图2所示。
Soil in Changxing Island, Shanghai……………YU Xuhua, CHEN Yilong(3·89)

图2 网侧PWM变换器拓补结构图
设三相电网电压平衡,电路中开关器件为理想开关,在三线制无中线系统中,三相电流相加和为零,且有三相电压平衡。通过坐标变化,容易得到网侧PWM变换器在坐标下的数学模型。

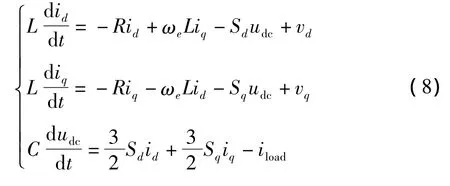

2.2 双馈风力发电机的两侧变流器控制策略
采用定子电压矢量定向,将同步旋转dq坐标系的d轴定向在电压矢量方向上,即vd=us,vq=0。由于网侧电压恒定,所以vd不变,有功功率、无功功率分别与id、iq成正比。推导可得:
式中,id和iq为网侧变流器输入三相电流在dq轴上分量;idc为网侧变流器直流母线上输出的电流;iload为网侧变流器直流侧的负载电流;vd和vq为电网三相电压在dq轴上分量;udc为直流母线电压;L为线路等效电抗;R为线路等效电阻;ωe为电网电压矢量旋转角速度;Si(i=1,2,3)为第i相的开关函数,Si的值满足式 (9),Sd和Sq为Si在dq轴上分量。
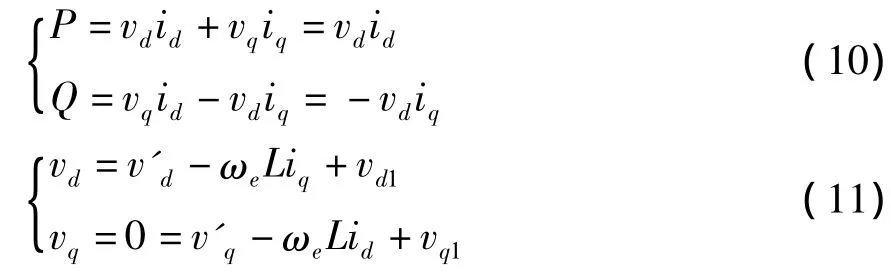
式中,v'd=Rid+vd1=Sdudc;vq1=Squdc。
如图3所示,改进后的网侧变流器控制目标是保证双馈风机有功-无功输出特性与实际相符,网侧变流器的控制策略是P和Q的瞬时功率闭环控制。Pref指令由直流母线电压通过PI调节器获得,Qref指令可由电网测得瞬时有功功率P经实测数据拟合函数计算得到。网侧电压源变换器的PWM调制波电压指令为

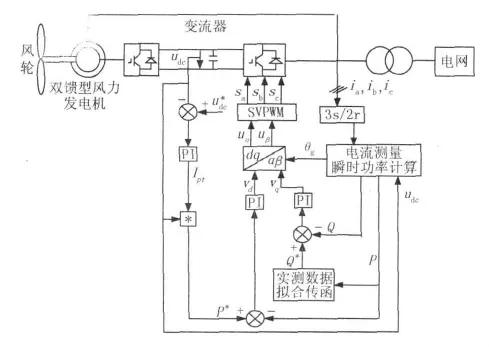
图3 网侧变流器改进控制结构
3 仿真分析
3.1 双馈风力输出特性仿真计算
在PSCAD环境下构建额定容量为2 MW的双馈风机模型,按照图3所示控制结构改进模型。其中,实测数据拟合函数确定的有功-无功调控模型如图4所示,主要参数如表1所示。

图4 由实测功率输出曲线确定的有功-无功调控模型

表1 2 MW双馈风机仿真系统的主要参数
利用单机无穷大系统对改进后模型进行校验,调节风速,使其从5 m/s缓慢上升到15 m/s,取不同风速下模型端口的稳态功率输出值,即有功功率和无功功率输出值,拟合得到风机功率输出特性曲线,如图5所示。图5(a)是由双馈型风机并网点实测数据获得的双馈风机功率输出特性曲线。图5(b)是现有模型的功率输出特性曲线,可以明显看出,现有模型在有功功率输出变化时,无功功率只在零附近小范围浮动,与实测数据得到的功率输出特性相差较大。图5(c)是双馈风机改进模型的功率特性曲线,该曲线与图5(a)中实测数据曲线的变化趋势是一致的。分别从图5(a)和图5(c)中取若干组数据进行误差分析,在有功功率输出值相同的情况下,无功功率的输出误差为e=(Q3-Q1)/Q1×100%,通过计算可得,误差范围小于±1%,证明该模型的准确有效。
3.2 含双馈型风电场局部网络暂态计算
在PSCAD/EMTDC环境下,建立了50 MVA的双馈型风电场并入电网的仿真系统,风电场采用单机大容量等效模型,仿真系统如图6所示。

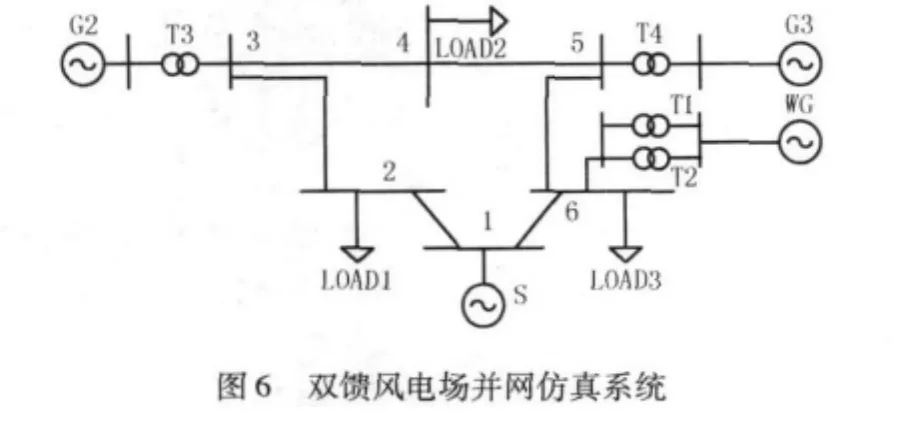
WG为等值风电场,其出口电压为13.8 kV,通过2台容量为20 MVA的升压变压器和架空输电线接入电网。S为等效外网,G2、G3分别是容量为60 MW的火力发电厂。Load1、Load2、Load3分别是容量为 (42+j17)MWA, (33+j12)MWA和 (30+j10)MWA的负荷。为了研究模型改进前后对系统暂态稳定计算的影响,分别设置了短路故障和负荷投切。
a. 短路情况
风速维持在12 m/s不变,设定故障为230 kV线路6中点处于1 s时发生单相接地短路故障,0.05 s后故障切除,线路恢复正常运行,最终达到新的运行状态。仿真得到母线6上模型改进前后的电压的幅值、频率和功角曲线,如图7所示。
由图7可以看出,故障发生后,母线电压幅值、频率都出现大幅跌落,故障排除后,对比与现有模型,在改进模型下,电压幅值和频率恢复过程中波动大,恢复速度快,功角波动却较小。
b. 负荷投切情况


风速维持在12 m/s不变,1 s时将负荷3切除,0.05 s后切入。仿真得到母线6上模型改进前后的电压的幅值、频率和功角曲线,如图8所示。
由图8可以看出,对比现有模型,在改进模型下,负荷的切入与切出使母线电压幅值只出现小幅波动,波动时间也相对较短;而对于频率和功角则出现了比较大的振荡,最高频率达到50.3 Hz,最低频率达到49.7 Hz,最大功角达到2.3°,最小功角达到 -3.3°。
4 结论
本文提出了一种双馈风机模型的改进方法,该方法利用双馈风机并网点实测数据,拟合获得实际运行中风机功率输出特性曲线,根据特性曲线改进双馈风机模型。对双馈型风力发电机并网运行的仿真分析结果如下。
a. 所提方法获得的双馈风机改进模型能真实有效地反映实际运行中的风机输出特性,应用改进模型得到的输出特性曲线与实测数据误差小于±1%。
b. 在短路故障和负荷投切计算中,双馈风机改进模型下,负荷投切操作的母线节点电压幅值在恢复的过程中波动相对较大,而进行短路故障节点频率和功角变化较为明显。因此,双馈风机仿真模型对风机输出特性描述的准确性会对含双馈风机的局部电网暂态计算结果有较大影响。
[1] 祝 贺,徐建源,张明理,等.风力发电技术发展现状及关键问题[J].华东电力,2009,37(2):314-316.
[2] 金 鑫.风力发电机组系统建模与仿真研究[D].重庆大学,2007.
[3] 高一丹,张步涵.并网双馈风力发电机组的建模与仿真[J].湖北工业大学学报,2010,25(1):75-80.
[4] 迟永宁,王伟胜,刘燕华.大型风电场对电力系统暂态稳定性的影响[J].电力系统自动化,2006,30(15):10-14.
[5] 李 晶,王伟胜,宋家骅.变速恒频风力发电机组建模与仿真 [J].电网技术,2003,27(9):14-17.
[6] 周先明.变速恒频双馈风力发电双 PWM变换器的研究[D].江南大学,2009.
[7] 魏 巍,王渝红,李兴源,等.基于PSASP的双馈风电场建模及接入电网仿真 [J].电力自动化设备,2009,29(12):68-73.
[8] 潘庭龙,纪志成.基于PSCAD的变速恒频双馈风电系统建模与仿真[J].控制工程,2009,16(6):771-774.
[9] 常鲜戎,于 啸,郭嘉阳,等.双馈型风力发电机无功控制模型参数灵敏度分析 [J].华北电力技术,2010,8(8):15-18.
[10] 申 洪.变速恒频风电机组并网运行模型研究及其应用[D].中国电力科学研究院,2003.
[11] 郝正航.双馈风电机组的暂态行为及其对电力系统稳定性影响[D].天津大学,2011.
[12] I.Erlich,H.Wrede,C.Felte.Dynamic Behavior of DFIGBased Wind Turbines during Grid Faults[J].Power Conversion Conference,Nagoya,Japan.2 -5 April 2007.
[13] Wang yulong,Lijianlin,Hu shuju.Analysis on DFIG Wind Power System Low-Voltage Ridethrough[J].International Joint Conference on Artificial Intelligence,Hainan,China.25-26 April2009.
[14] 祝愿博.基于DSP与430单片机的电能质量测量仪设计[D].武汉科技大学,2010.
[15] 徐小丽.拉格朗日插值法在工程应用中的算法实现 [J].林区教学,2010(1):17-19.
