黏性介质叠前时间偏移方法

李雪英，文慧俭，张 桐，于国楠，王金丽

（1．东北石油大学地球科学学院，黑龙江大庆 163318； 2．大庆油田博士后科研工作站，黑龙江大庆 163458； 3．东北石油大学博士后科研流动站，黑龙江大庆 163318； 4．大庆油田有限责任公司第三采油厂，黑龙江大庆163113； 5．大庆油田有限责任公司第二采油厂，黑龙江大庆 163416）

黏性介质叠前时间偏移方法

李雪英1，2，3，文慧俭1，张 桐4，于国楠5，王金丽5

（1．东北石油大学地球科学学院，黑龙江大庆 163318； 2．大庆油田博士后科研工作站，黑龙江大庆 163458； 3．东北石油大学博士后科研流动站，黑龙江大庆 163318； 4．大庆油田有限责任公司第三采油厂，黑龙江大庆163113； 5．大庆油田有限责任公司第二采油厂，黑龙江大庆 163416）

根据衡Q模型，将吸收系数引入黏性介质的相速度中，以相移法为基础，利用稳相点原理，推导基于叠加速度和等效Q值的黏性介质叠前时间偏移的走时和振幅计算公式，研究适合于黏性介质的叠前时间偏移方法．理论数据处理结果表明，该方法具有精确的复杂构造成像能力，能够将黏性补偿结合到偏移过程中，有效恢复深层界面的高频信息；在准确构造成像的同时，提高地震成像的分辨率．

叠前时间偏移；黏性吸收补偿；等效Q值；稳定性控制；黏性介质

0 引言

在常规叠前时间偏移过程中，忽略地震波能量的吸收与频散效应是不合理的．因此，人们提出应该在剔除地震波传播效应的同时，完成对地震波能量补偿的黏性介质偏移．黏性补偿技术包括两类：一类是反Q滤波算法；另一类是黏性介质深度偏移算法．在早期的黏性补偿技术中，反Q滤波算法得到快速发展．Hargreaves N D等提出一种与Stolt偏移算法类似的反Q滤波算法，通过引入类似于Stolt偏移的坐标变换，利用快速Fourier变换，可以有效地校正时变的相位扭曲［1—2］．基于地震波场延拓理论，Wang Y H提出一种适用于水平层状和Q值随时间或深度连续变化，并且可以同时完成幅度补偿和相位校正的反Q滤波算法［3—5］．反Q滤波技术无法处理Q值横向变化的叠前地震资料，因此在地震资料处理中的应用价值受到限制．

为了能够将黏性补偿技术推向叠前地震资料处理中，人们提出黏性介质叠前深度偏移算法．Mitte R等根据黏性介质叠前深度偏移的基本思想，建立黏性介质的声波波动方程及其波场延拓方法，给出适用于黏性介质偏移的成像条件，并进行相应的数值算例验证［6—7］．Causse E等实现黏性介质的逆时偏移成像［8—9］．Emmerich H、Carcione J M和Stekl I等在地震正演模拟中，以及Keers H等在反演中考虑地震波能量被吸收的实际效果，模拟地震波在地下真实传播情况［10—13］．Zhang J F等采用加权最小平方法，设计最优空间褶积短算子适应介质横向变化，通过限制波场最大传播角度的策略，实现算法稳定性，给出黏性非均匀介质叠前深度偏移的精确成像，提高算法的精度与效率［14］．这些研究主要集中在对黏性介质叠前深度偏移的论述上，对于黏性介质的叠前时间偏移方法鲜有论及．

笔者根据稳相点原理，推导黏性介质叠前时间偏移的高频渐进解公式，引入等效Q值，使得黏性介质叠前时间偏移方法可以应用到叠前地震资料的高分辨率成像处理中，解决反Q滤波不能处理Q值非均匀的叠前资料及黏性介质叠前深度偏移层状Q值建模问题．

1 理论推导

1．1 走时及振幅

基于单程波方程和稳相点理论，参考深度偏移方法研究黏性介质叠前时间偏移中走时及振幅计算方法［15—19］．对于水平层状介质，炮和单道数据可以统一看作空间脉冲函数，在频率—波数域用f（ω）表达，基于深度偏移相移法，对于水平层状黏性介质波场的深度延拓［15，20］可以表示为

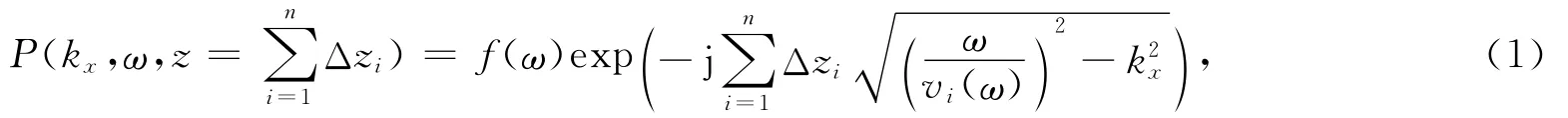
式中：j为虚数单位；ω为频率；kx为水平波数；P（kx，ω，z）为深度为z处的频率—波数域波场；Δzi为各层介质的厚度；n为目的层以上的介质层数；f（ω）为炮点或检波点的时域信号的傅立叶变换；vi（ω）为各层复速度，且

式中：vi为各层的实相速度；Qi为各层的品质因子．用时间表示波场延拓步长，对于黏性介质，在地面波场延拓到T深度的波场为

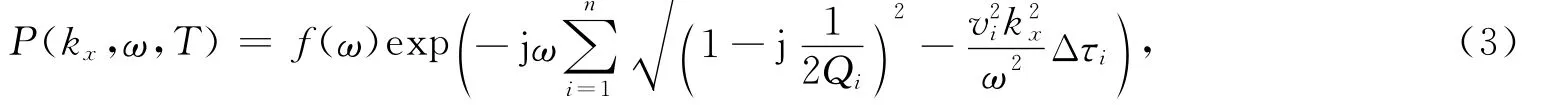
式中：T为单程旅行时表达深度；Δτi为各层的时间厚度，为深度T处频率—波数域波场．

令px＝kx／ω，则式（3）的指数函数的指数项可近似表达为

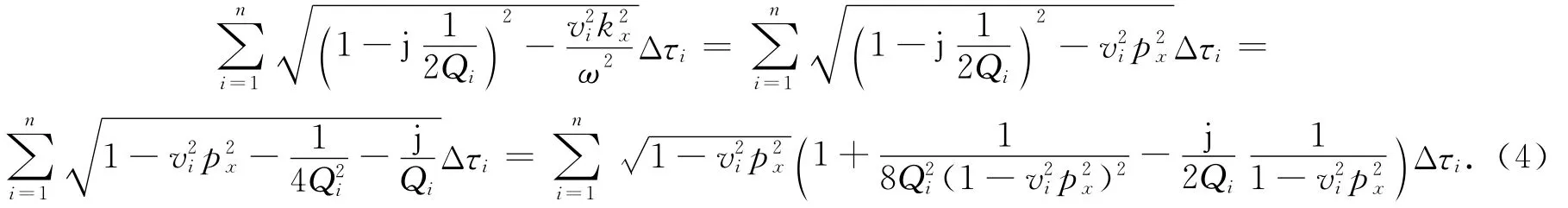
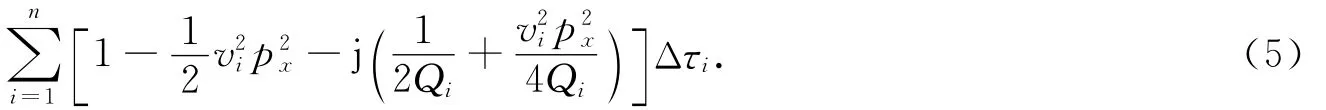
令

式中：vrms为均方根速度；Qeff为等效Q值；vQrms为与Q有关的速度，在实际应用时可以近似等于均方根速度．

将式（5）和式（6）代入式（3），做空间Fourier反变换，得到空间—频率域波场：

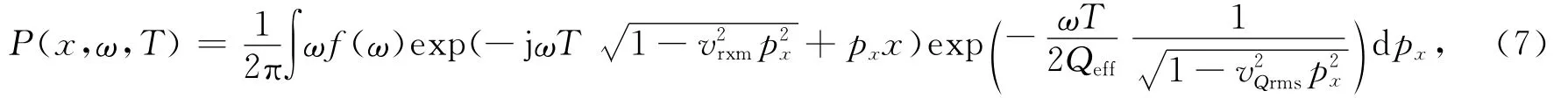
式中：x为炮（检波）点到成像点之间的水平距离；px为射线参数，与频率无关，令

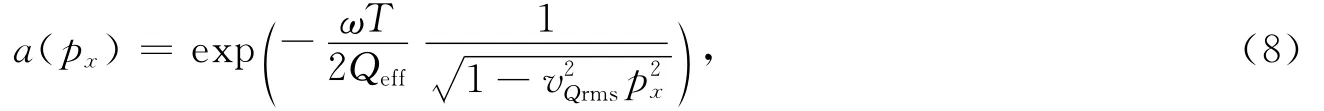
对式（9）求取一阶和二阶导数得

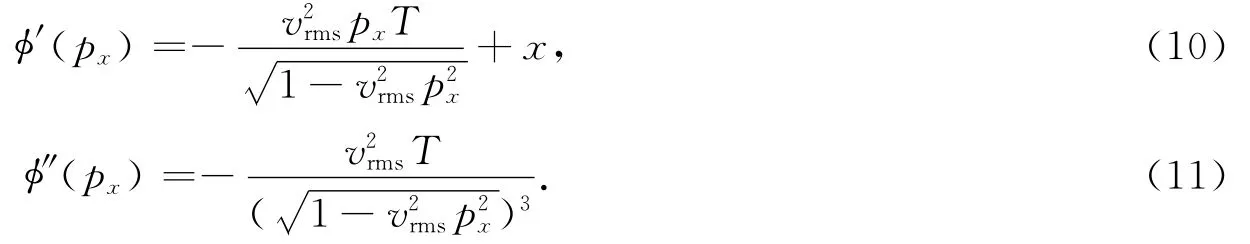
应用稳相点原理，对式（7）求得黏性吸收介质相移公式的渐进解：

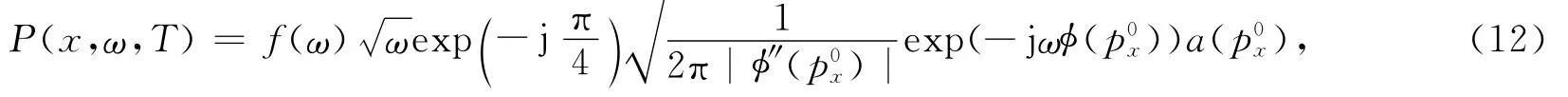
式中：p0x为φ′（px）的零点，为成像点所对应的射线参数，即稳相点．令φ′（px）＝0，解得：

将p0x代入式（11）得：

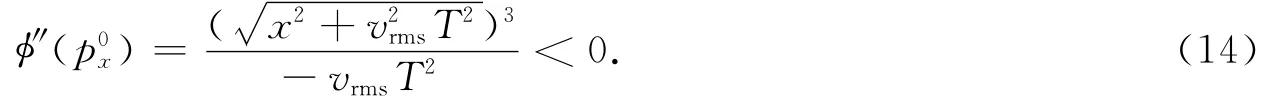
将p0x，φ″（p0x）代入式（9）、式（11）、式（8），得到地震波从源点（0，0）到（x，T）的走时t、振幅A和吸收Θ 为

当ω大于2Hz时，式（12）是式（7）的很好近似，对于地震勘探是满足的，因此可以将式（12）作为频率域—空间波场的解析表达式．

由式（12）定义下行波在吸收介质的正向传播算子为

其中下标B代表吸收介质．

为了能够推导吸收介质中上行波的逆向传播算子，假设存在一种与吸收介质相伴随的补偿介质，体积模量定义为

式中：＊为复共轭符号；M′（ω）为补偿介质的体积模量，与吸收介质的体积模量互为复共轭．补偿介质只是为了计算方便而引入的一种与吸收介质相伴随的表达方式（下标A表示）．

Zhang J F给出吸收介质和补偿介质上、下行波的正向传播算子与逆传播算子之间的关系［14］：

由互易定理得：

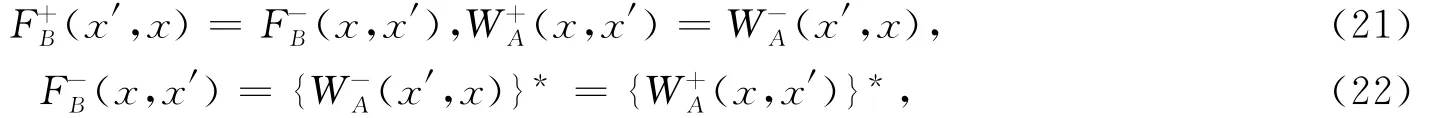
同理，可得：

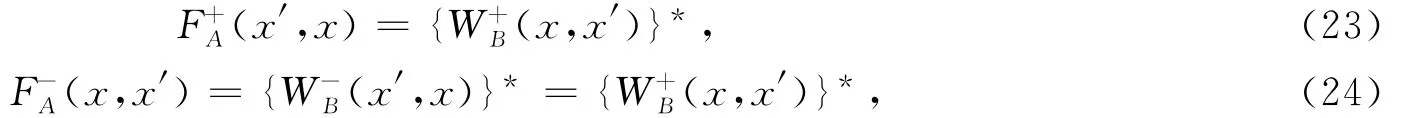
式中：x′为炮点或者检波点坐标；x为成像点坐标；F+A、F+B为下行波在补偿介质和吸收介质中的逆向传播算子；F—A和F—B为上行波在补偿介质和吸收介质中的逆向传播算子；W+A、W+B为下行波在补偿介质和吸收介质中的正向传播算子；W—A、W—B为上行波在补偿介质和吸收介质中的正向传播算子．

由式（20）和式（22）或式（23）和式（24）给出吸收介质逆向传播算子和补偿介质正向传播算子之间的转换关系，即互为复共轭；反之，亦然．对于黏性介质叠前时间偏移，吸收介质中的上行波场向下延拓可以通过对波场乘以逆向传播算子完成；下行波场的向下延拓根据不同的成像条件选择不同的正向传播算子；如果是在吸收介质中延拓，则选取W+B（x，x′）；在补偿介质中延拓，则选择W+A（x，x′）．

1．2 成像条件

有2种成像条件可以用于黏性介质的偏移成像，第一种是反褶积成像条件：

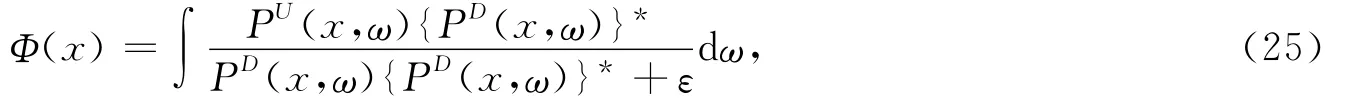
式中：PD（x，ω）为吸收介质中正向延拓的下行波场；PU（x，ω）为吸收介质中反向延拓的上行波场；ε为一个很小稳定性常数．董春晖分别考察单极源和偶极源采用褶积成像条件，可以实现叠前时间偏移的保幅处理［］．

第二种成像条件是在补偿介质中设计一个正向外推算子，以增强波场．该正向算子与吸收介质的逆向传播算子互为复共轭（见式（23）），因而很容易获取算子．如果设［PD（x，ω）］′为补偿介质中的正向延拓下行波场，则第二种成像条件（相关成像条件）可以表达为

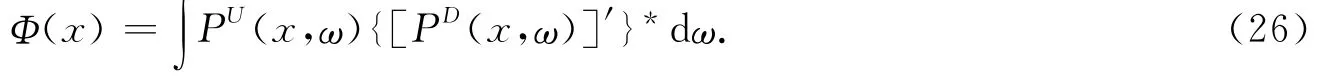
该成像条件首先由Mittet R等提出［6］，后由Causse E等给出严格的数学证明［9］．Zhang J F通过数值算例证实，褶积成像条件与相关成像条件相比可以很好地压制噪声，从而给出更加清晰的成像而实现保幅处理［14］，文中选用反褶积成像条件．

1．3 稳定性控制

黏性介质叠前时间偏移成像是通过设计补偿算子完成地震数据的高频补偿，但是在高频恢复过程中也会增强高频噪声，使算法表现固有的不稳定性．因此，稳定性控制成为黏性介质偏移成像和反Q滤波最为关键的问题．

为了使噪声在偏移过程中不出现不必要的扩大，设计一个适用于高频的补偿算子．重新构造一个以自变量为χ（χ＝ωT）的补偿函数Γ（χ），设置截止值χc，当χ≤χc时，补偿函数为原有精确的补偿算子；当χ＞χc时，补偿算子经过一个一阶光滑可导函数改造后而渐变为最大的振幅门限值Glim，经过改造后的补偿函数Γ（χ）随着χ变化与精确补偿算子对比结果见图1（实线为原有的补偿算子的模，虚线为改造后的模）．该方法可以保持高频的振幅恢复，对深层和远偏移距的很弱有效信息进行最大限度恢复与补偿，虽然在改造过程中不可避免地增强背景噪声，但是噪声在叠前偏移后的共反射点叠加中得到有效压制．

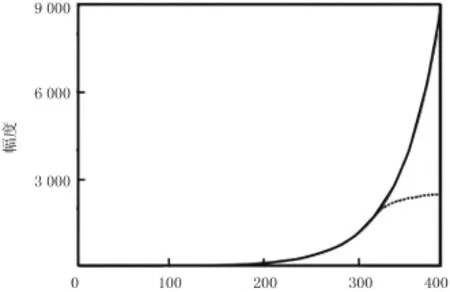
图1 补偿算子与经过改造后的补偿算子谱Fig．1 The comparison of compensation operator spec—trum with spectrum after smoothing

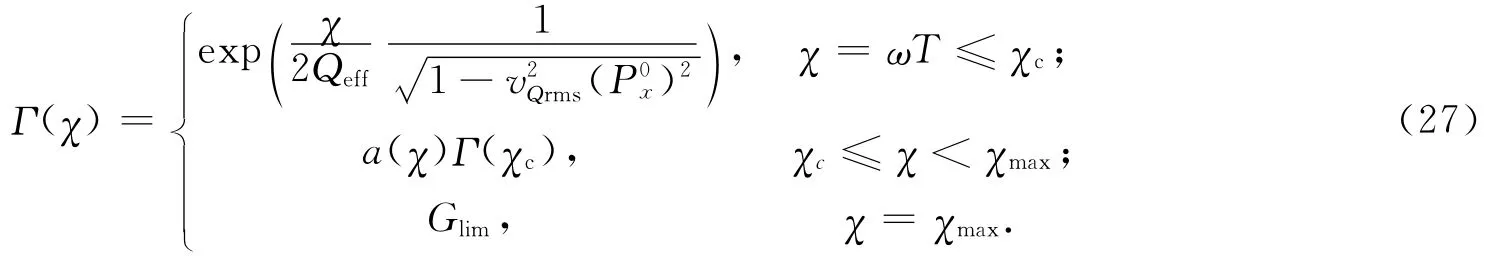
式中：a（χ）为一阶光滑可导函数．

2 模型验证

采用二维频域有限差分方法双程声波波动方程，建立黏性介质的衰减正演模拟理论模型．正演模拟的宏观介质参数模型见图2．模拟后的数据包含51个共炮点道集，震源采用的是最大频率为55Hz的雷克子波，炮点分布位置为447．75～3 147．75m，炮间距为54m；每炮为800道，检波点间距为4．5m；记录长度为1．68s，采样间隔为4ms；在模型两侧每边共设20个网格点的衰减区，以减少边界反射．为了保证模拟数据更接近真实数据，在模拟中保留表面多次波和层间多次波．

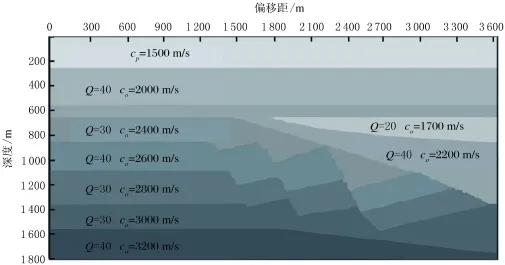
图2 正演模拟的宏观介质参数模型Fig．2 Subsurface real phase velocity and Q model

采用共反射点叠加方案，对模拟的理论数据进行常规叠前时间偏移和黏性介质叠前时间偏移（见图3和图4）．由图3和图4可以看出，2个成像剖面上所有反射轴正确归位且精确成像；在模型右侧的楔状体处，波从高速介质入射到低速介质，波形出现极性反转．在常规叠前时间偏移成像剖面上，由于地震波在传播过程中存在衰减和频散，地震波的能量随着深度增加而逐渐减弱；使得深层反射界面成像模糊，振幅减弱，分辨率较差．为了更好地显示分辨率改善效果，在增益后的图像中任意选择5处设定标尺，然后在黏性补偿剖面中按照相同的长度画出，在对吸收给出正确补偿后（见图4），所有界面得到正确构造归位，深层记录频带得到拓宽（见图5），不考虑黏性补偿的时频谱见图5（a），考虑黏性补偿的时频谱见图5（b）．由图5可以看出，空间子波被压缩，振幅增强，分辨率提高．

图3 常规叠前时间偏移结果Fig．3 The profile of conventional prestack time migration

图4 考虑黏性补偿的叠前时间偏移结果Fig．4 The prestack time migration profile of compensation for anelastic absorption

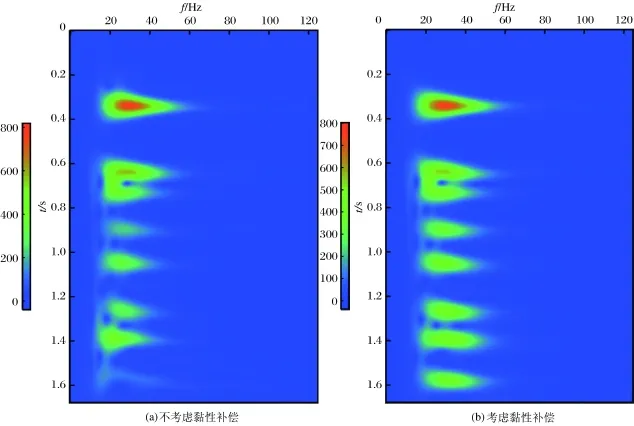
图5 广义S变换前后时频谱Fig．5 The comparison time frequency spectrum gained by generalized S transform

从2个成像剖面同一位置处抽取一道数据，利用广义S变换进行时频分析（见图5）．在不考虑黏性补偿的时频谱上，随着深度的增加，地层子波的频带逐渐变窄，峰值频率向低频移动．经过黏性补偿后，深层的子波频带得到恢复，峰值频率向高频移动，深浅层的子波频带宽度保持一致．

理论数据处理结果表明：文中给出的方法在对非均匀吸收介质进行正确构造成像的同时，可以完成保幅、提高分辨率的地震处理要求，在成像过程中体现考虑黏性补偿的重要性．

3 结束语

文中给出的方法将黏性补偿结合到偏移过程中，能够很好地完成对吸收与频散的补偿；深层界面信息得到有效恢复，频带拓宽，振幅增强；地震剖面分辨率得到明显提高．在精确构造成像的基础上，能够丰富地震信息，为后续的地震解释奠定基础．

［1］ Hargreaves N D，Calvert A J．Inverse Q filtering by Fourier transform［J］．Geophysics，1991，56（1）：519—527．

［2］ Hargreaves N D．Similarity and the inverse Q filter：some simple algorithms for inverse Q filtering［J］．Geophysics，1992，57（2）：944 —947．

［3］ Wang Y H．A stable and efficient approach of inverse Q filtering［J］．Geophysics，2002，67（2）：657—663．

［4］ Wang Y H．Quantifying the effectiveness of stabilized inverse Q filtering［J］．Geophysics，2003，68（1）：337—345．

［5］ Wang Y H．Inverse Q—filter for seismic resolution enhancement［J］．Geophysics，2006，71（3）：V51—V60．

［6］ Mittet R，Sollie R，Hokstad K．Prestack depth migration with compensation for absorption and dispersion［J］．Geophysics，1995，60 （5）：1485—1494．

［7］ Mittet R．A simple design procedure for depth extrapolation operators that compensate for absorption and dispersion［J］．Geophysics，2007，72（2）：S105—S102．

［8］ Causse E，Ursin B．Asymptotic error analysis of constant—velocity viscoacoustic migration［J］．Geophysics，1999，64（4）：1036—1045．

［9］ Causse E，Ursin B．Viscoacoustic reverse—time migration［J］．Journal of Seismic Exploration，2000，9（1）：165—184．

［10］ Emmerich H，Korm M．Incorporation of attenuation into time—domain computations of seismic wavefields［J］．Geophysics，1987，52 （9）：1252—1264．

［11］ Carcione J M，Kosloff D，kosloff R．Wave propagation simulation in a linear viscoelastic medium［J］．Geophysics Journal Interna—tional，1999，95（3）：597—611．

［12］ Stekl I，Pratt R G．Accurate viscoelastic modeling by frequency—domain finite differences using rotated operators［J］．Geophysics，1998，63（5）：1779—1794．

［13］ Keers H，Vasco D W，Johnson L R．Viscoacoustic cross—well imaging using asymptotic waveforms［J］．Geophysics，2001，66（3）：861—870．

［14］ Zhang J F，Wapenaar K．Wavefield extrapolation and prestack depth migration in anelastic inhomogeneous media［J］．Geophysical prospecting，2002，50（6）：629—643．

［15］ Gazdag J．Wave equation migration with the phase—shift method［J］．Geophysics，1978，43（7）：1342—1351．

［16］ Bleistein N，Cohen J K，Stockwell J W．Mathematics of multidimensional seismic inversion［M］．Berlin：Springer，2001．

［17］ Zhang J F，Wapenaar C P A．High—resolution depth imaging with sparseness—constrained inversion［J］．Geophysical Prospecting，2006，54（1）：49—62．

［18］ Zhang Jianfeng，Liu Linong．Optimum split—step Fourier 3Ddepth migration：Developments and practical aspects［J］．Geophysics，2007，72（3）：S167—S175．

［19］ Claerbout J F．Imaging the earth＇s interior［M］．Oxford：Blackwell Scientific Publications，1985．

［20］ 董春晖，张剑锋．起伏地表下的直接叠前时间偏移［J］．地球物理学报，2009，52（1）：239—244．Dong Chunhui，Zhang Jianfeng．Prestack time migration including surface topography［J］．Chinese Journal of Geophysics，2009，52 （1）：239—244．

TE132．1

A

2095—4107（2013）04—0098—07

DOI 10．3969／j．issn．2095—4107．2013．04．015

2013—07—05；编辑：任志平

国家科技重大专项（2011ZX05008—006—42）；黑龙江省博士后基金项目（LBH—Z12002）；黑龙江省教育厅科技项目（12513069）

李雪英（1972—），男，博士，教授，主要从事地震波传播与成像方面的研究．

文慧俭（1972—），女，博士，副教授，主要从事油田开发地质方面的研究，whjdqpi＠163．com．