一种云模型PID控制器参数整定优化算法

魏连锁，孙 明，张媛媛，张恩鸣

（1．齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔 161006； 2．大庆油田有限责任公司电力集团，黑龙江大庆 163451； 3．大庆油田有限责任公司天然气分公司，黑龙江大庆 163414）

一种云模型PID控制器参数整定优化算法

魏连锁1，孙 明1，张媛媛2，张恩鸣3

（1．齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔 161006； 2．大庆油田有限责任公司电力集团，黑龙江大庆 163451； 3．大庆油田有限责任公司天然气分公司，黑龙江大庆 163414）

为了解决PID控制器参数整定过程中的优化和复杂性问题，增强PID控制器参数整定的自适应性，结合差异演化算法和粒子群算法，提出一种带有差异演化变异算子的粒子群混合优化算法，利用一维云模型映射器将人的控制经验通过语言原子转换为控制规则器，设计具有自适应功能的云模型控制器；将该优化算法应用于一维云模型PID控制器参数整定与优化，并与传统方法进行仿真比较．结果表明，基于带有差异演化变异算子的粒子群混合优化算法的智能控制器具有简单易行、控制性能良好、自适应性和鲁棒性强的特点，可为云模型控制器参数设计提供参考．

PID控制器；云模型；差异演化；粒子群；混合算法

0 引言

PID控制器设计原理简洁、参数调整方便，在工业过程控制设计中被广泛应用［1—5］，PID控制器的设计与应用是控制器参数的整定与优化的关键问题之一．PID参数整定与优化方法可以分为常规PID参数和智能参数整定与优化．其中常规PID参数整定方法通常采用经验法和凑试法［6—7］等，在生产过程中对具有非线性、时滞、时变、对象不确定及多输入多输出系统进行控制时，难以达到控制要求和效果．随着智能算法的不断发展，人们提出一系列PID控制器参数的整定与优化方法，包括基于差异演化算法［8—9］和粒子群算法［10］等参数整定与优化方法．这些研究不仅在算法的优化性能上存在不足，而且在PID参数的设置选取上依靠人工经验，缺乏自适应性．

粒子群优化（Particle Swarm Optimization，简称PSO）算法是通过种群个体粒子之间的相互合作与竞争产生群体智能指导优化搜索算法．与差异演化算法和遗传算法相比，它具有算法简单、易实现、计算量少和计算复杂度低等优点［11—13］，但是PSO算法在解空间搜索后期容易陷入局部最优解，产生早熟、停滞现象．虽然人们不断改进PSO算法，如通过动态调整PSO的惯性权重系数、增加粒子群规模等，但不能从根本上克服早熟收敛现象．差异演化（Differential Evolution，简称DE）算法是一种基于群体差异的演化算法，具有全局并行直接搜索的特点，当种群中个体差异较小时，表现较强的局部搜索能力．特别是在求解非凸、多峰、非线性多目标函数优化时，具有较强的稳定性和收敛速度，成功应用于热交换机的优化与设计、多模态控制优化等．因此，利用差异演化增强粒子群的全局搜索和局部搜索能力，能够有效提高粒子群的优化性能［14］．

在选取PID控制器参数时，往往依赖于人工的控制经验，从而影响控制器的自适应性［15—16］．云模型是在随机数学和模糊数学基础上，提出的一种实现定性概念与定量数据相互转换的不确定性转换模型．它用云的数字特征期望、熵和超熵表示语言值的数学性质，实现定性语言值和定量数值之间的转换．利用云模型可以将人工的控制经验通过语言原子转换到语言控制规则器中，能够设计不需要系统具体数学模型、不受系统外部因素影响的且具有较好自适应性的云模型控制器．

笔者结合差异演化与粒子群算法，提出一种带差异演化变异算子的粒子群混合优化算法，并应用于一维云模型PID控制器参数整定与优化．与传统算法进行仿真对比，得到各自的阶跃响应控制效果，表明提出的混合优化算法具有更好的优化效果．

1 PID控制器

1．1 一维正态云模型

设R（E，σ）为服从高斯分布的随机函数，E为期望值，σ为标准差，将满足公式的数据对drop（xi，pi）（i＝1，2，3，…）构成的云模型称为一维正态云模型（简称一维正态云［16］），其中Ex，En和He分别为云模型的期望值、熵和超熵，表示为CG（x）．一维正态云模型的数字特征为（Ex，En，He），用matlab 7．0生成的图形见图1．由图1可以看出，它既不是明确的隶属函数曲线，也不是确定的概率密度函数，是像云朵一样的一对多的数学映射图像；所以借用“云”定义数据和概念之间的数学模型转换理论．

1．2 云模型多规则映射器

控制器所实现的输入输出控制关系本质上是一种映射过程，即从偏差输入到控制量输出的映射．考虑一维云模型映射器（见图2），它由一维云模型多规则推理部分和加权平均处理部分组成．每个映射关系由一组（Ex，En，He）IF—THEN规则完成，其中每个规则描述（Ex，En，He）局部的行为映射．输入x刺激前件部分CGA1～CGAN，产生不同的μNj；再经后件部分CGU1～CGUN进行处理，形成许多的云滴drop（yNj，μNj）；将得到的云滴经过加权平均处理后，得出与输入x相对应的输出值yi．

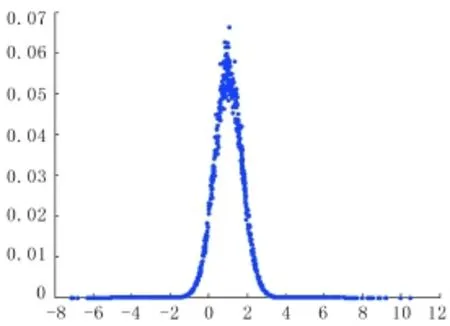
图1 一维正态云模型Fig．1 One—dimensional normal distribution cloud model

1．3 一维云模型PID控制器

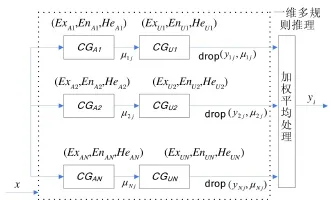
图2 一维云模型映射器Fig．2 One—dimensional cloud model mapper

一维云模型PID控制器见图3，其中参数e∈E，ei∈Ei，ec∈Ec，分别为控制器偏差、偏差积分和偏差变化率；Kup、Kui、Kud分别为云模型PID的输出驱动因子；U为一维云模型PID控制器的输出，调节被控对象．一维云模型映射器经过定量输入e、ei和ec计算输出控制分量uP、uI、uD．根据PID控制器的物理意义，uP、uI、uD具有类似传统PID控制器的3个控制分量的比例控制、积分控制和微分控制功能，但本质不同．一维云模型PID控制器的输出控制分量uP、uI、uD并不是简单的比例控制、积分控制和微分控制，它可以按照被控制对象的变化进行有效自动调节控制对象，还能根据工程需要满足被控制对象所需的各种线性和非线性的映射要求，是传统的PID控制器不能完成的．

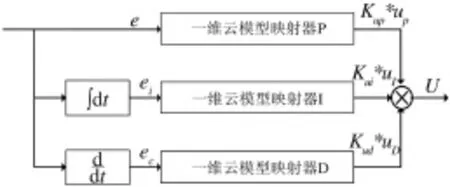
图3 一维PID云模型控制器Fig．3 One—dimensional PID cloud model controller

2 差异演化与粒子群混合算法

标准的PSO算法实现方便、概念简明、参数设置少、收敛速度快，是一种比较高效的搜索算法，但是也存在容易陷入局部最优、“早熟”等缺点．文献［17］对标准的PSO算法进行适当改进，避免陷入局部最优的情况，以求得到全局最优解．借鉴差异演化算法的变异算子操作，当选定粒子个体后，在粒子个体上加上2个个体带权的差而生成变异算子．在迭代初期，由于种群中粒子个体的差异相对较大，变异操作使算法本身具有较强的全局搜索能力；随着迭代次数增加，当趋于收敛时，种群中粒子个体的差异相对较小，使得算法具有较强的局部搜索能力．

利用差异演化算法引入变异算子：先将种群中的个体粒子赋给变异算子概率p，并且算法每进行一次迭代运算，就根据变异算子概率在种群里选出一定数目的粒子，将选出的粒子进行随机两两交叉、变异生成同样数目的粒子作为子代，再用新生成的子代取代原种群中的粒子父代．这样既保持种群总的粒子数量不变，也保证种群粒子的多样性．令m与n是2个父代粒子，则对其进行变异算子交叉操作：

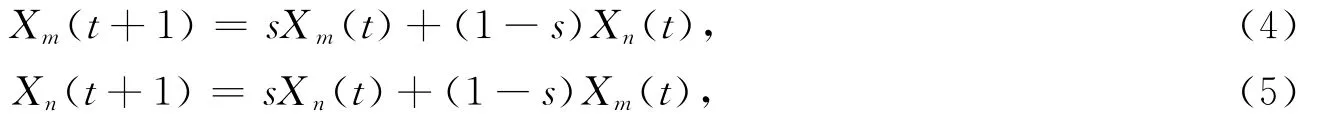
式中：Xm（t）、Xn（t）为粒子变异前的2个当前位置；Xm（t+1）、Xn（t+1）为粒子经过变异算子变异后的2个新位置；0＜s＜1．经过差异演化算法相应的交叉、变异、选择操作，在父代个体粒子中随机产生2个新的位置，在整个粒子群保证多样性，提高粒子群算法在搜索解空间的遍历速度，也避免陷入局部最优，从而求得全局最优．

3 D—PSO算法优化云模型PID参数

云模型PID控制器模型描述为

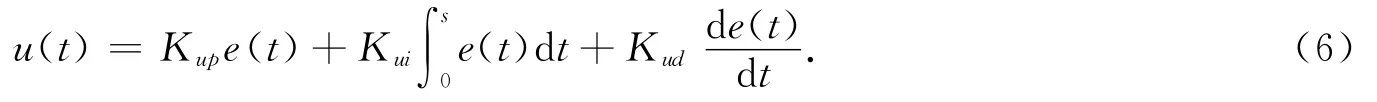
云模型PID控制器参数的优化是将Kup，Kui，Kud参数利用D—PSO算法进行优化，实质是利用一定目标函数对参数进行寻优．文中采用的目标函数为

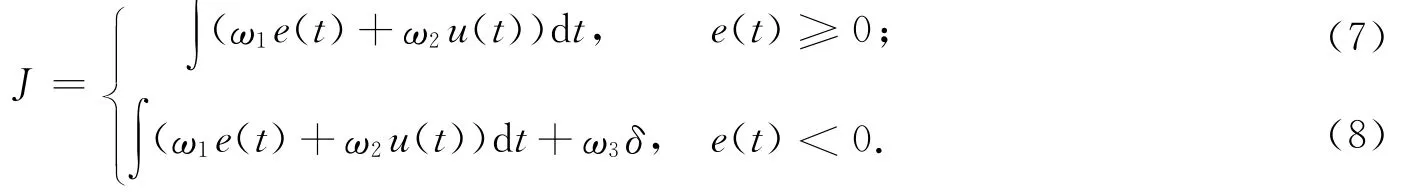
式中：e（t）为输入与输出的偏差量；u（t）为云模型PID控制器的输出控制量；ω1，ω2，ω3为权值系数，ω1+ω2+ω3＝1．如果有超调出现，则加入超调调节因子δ，以抑制超调的作用．

用Ji表示种群粒子当前的适应值；Jibest表示经历过种群粒子个体的最好适应值；Pi表示对应Jibest上的位置；Jgbest表示经历过种群粒子的全局最好适应值；Pg表示对应Jgbest上的位置．云模型PID控制器参数优化的步骤为：

（1）初始化PID控制器的参数取值范围和D—PSO算法的控制参数vmax，并随机产生种群中粒子的初始位置xi和速度vi．

（2）利用式（7）、式（8）计算目标函数适应度函数Ji．

（3）在种群中个体粒子：如果Ji＞Jibest，则Jibest＝Ji，Pi＝xi；如果Ji＞Jgbest，则Jgbest＝Ji，Pg＝xi．

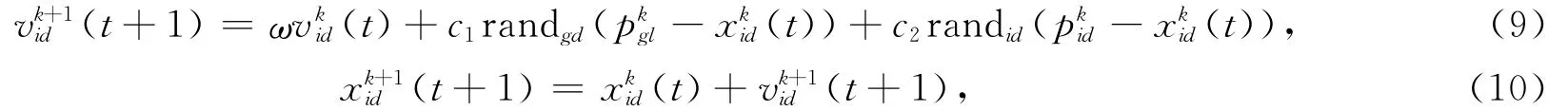
（4）利用公式更新微粒的速度与位置．其中：ω为惯性权重；η为速度权重约束因子为粒子的当前位置为粒子的当前速度为粒子个体最优位置为群体最优位置；c1，c2为权重因子；randgd、randid是在［0，1］之间生成的随机数．文中取c1、c2为［0，2］的随机数

（5）根据差异演化算法，由式（4）、式（5）计算适应度高的粒子替代个别适应度低的粒子，对粒子群进行变异、交叉操作，以实现对粒子群算法的改进．

（6）如果未满足结束条件，则返回步骤（2）．

4 D—PSO算法收敛分析

定理标准PSO算法是局部收敛算法．

证明令a1＝c1randgd，a2＝c2randid，a＝a1+a2．设算法中全局最优位置p4gl、个体最优位置pikc、惯性权重ω、a1与a2为常数时不变，并将算法简化到一维进行分析，则式（9）化简为

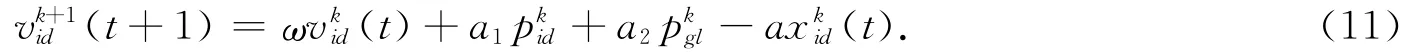
令式（11）中t＝t+1，可得：

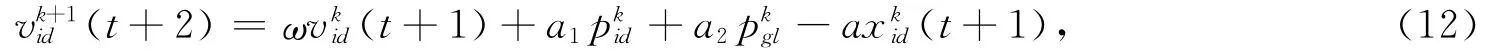
将式（10）代入式（12）可得：

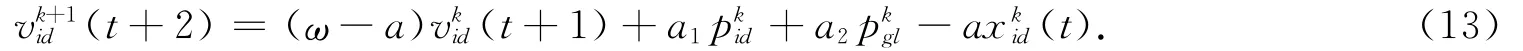
综合式（11）与式（13）可得速度的差分方程：

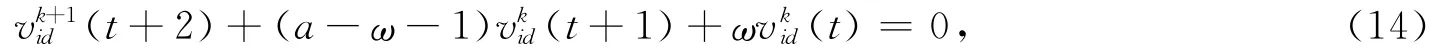
对应式（14）的特征方程为

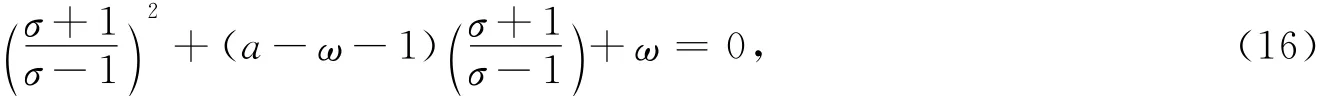
整理化简：

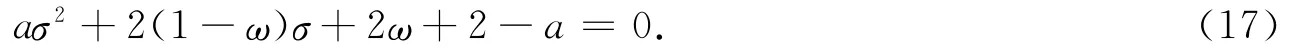
由劳斯—赫尔维格判据可得，当满足式（17）时，系统渐进稳定：

再由特征根法，求得系统收敛于

式中：tmax为最大进化代数．式（19）表明，标准PSO算法参数满足式（18）时，种群中粒子的速度将趋于0，位置收敛于

推论标准PSO算法的局部收敛是D—PSO算法收敛的充分条件．

证明D—PSO算法的进化机制是在标准PSO算法处于收敛状态后应用差异演化算法进行优化．差异演化算法并未修改标准PSO算法的进化机制和参数，只是更新标准PSO算法的全局最优位置．D—PSO算法只修改标准PSO收敛分析方程中的pkgl，并未修改算法的其他参数．因此，式（13）对算法D—PSO同样成立．

5 实验仿真分析

在matlab 7．0仿真环境下，采用二进制编码形式，利用D—POS算法对云模型PID控制器的参数进行优化．首先对式（6）中的Kup，Kui，Kud进行优化；再对偏差、偏差微分、偏差积分（E，EC，EI）及对应的输入（UE，UEC，UEI）进行优化，共30个数字特征（见表1）．其中：偏差E（UE）（Ex1，En1，He；…；EX5，En5，He），偏差微分EC（UEC）（Ex1，En1，He；…；EX5，En5，He），偏差积分EI（UEI）（Ex1，En1，He；…；EX5，En5，He）．

云模型PID控制器参数的优化设计过程：首先在定义域内随机生成初始参数组合，经过差异演化算法的变异、交叉、选择产生下一代，将经过优化的第一代参数代入式（6），计算相应参数所对应的e（t）、u （t）；再利用D—PSO算法，根据种群粒子适应度F（其中F＝1／J）调整参数值及参数组合；然后将调整后的参数组合赋给被控对象进行仿真计算，如此反复，直至达到要求结果．

采用D—PSO算法经过27代优化后的云模型PID控制器参数见表2．将表2的参数应用于文献［8］的被控对象式中：

阶跃响应性能曲线见图4．单位阶跃信号作用下的性能指标见表2．由图4可得，云模型PID控制器在优化前有超调，调节时间约为5．13s，后趋于稳定；优化后无超调，在1．56s后基本稳定．

有延迟的阶跃响应性能曲线见图5．由图5可得，采用延迟时间1．035s时，文献［8］控制方式恢复到稳定状态时间过长，难以达到实际控制系统要求；D—PSO改进云模型PID控制器很快恢复到稳定状态，表现较好的鲁棒性．

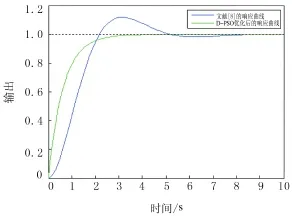
图4 阶跃响应性能曲线Fig．4 Comparison curves of step response per—formance

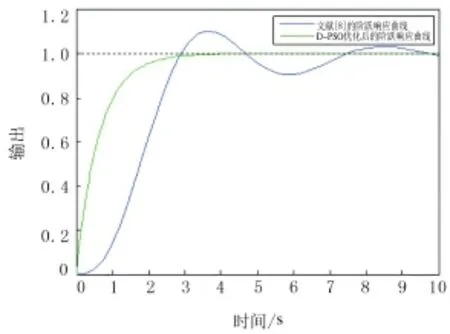
图5 有延迟的阶跃响应性能曲线Fig．5 Comparison curves of the delayed step re—sponse performance

表1的参数是经过大量工程设计经验和实验调试而得到的一组特征参数；根据D—PSO算法的自寻优特点，找到适合控制器特征参数，从而缩短设计周期（见表3）．经过D—PSO优化后的云模型PID控制器在超调时间、稳态精度上也有明显改善；在控制对象结构发生变化时，也表现相对较强的鲁棒性．

表1 文献［8］的云模型数字特征Table 1 Feature list of the numerical characteristics of cloud model in reference［8］

表2 输出量化因子Table 2 Output quantifying factor

表3 D—PSO方法特征参数Table 3 D—PSO method characteristic parameters

6 结论

提出一种基于差异演化和粒子群的混合优化算法，通过借助差异演化变异算子较强的全局搜索和局部搜索能力，改进粒子群的优化性能；利用云模型的数字特征参数和控制规则，设计一维云模型PID控制器．在对一维云模型PID控制器参数优化过程中，混合算法能较快找到全局最优参数，并且收敛速度和精度都优于基本粒子群算法，有效克服算法容易陷入局部最优的缺陷．仿真实验结果表明，提出的方法优于文献［8］的差异演化算法，设计的PID控制器，在云模型PID控制器的超调时间、稳态精度上有较大改善，并且对控制对象结构的变化也具有较强的鲁棒性．

［1］ Hua Y．Estimating two—dimensional frequencies by matrix enhancement and matrix pencil［J］．IEEE Trans．Signal Process，2001，40 （9）：2267—2280．

［2］ Lank G W，Reed I S，Pollon G E．A semi coherent detectionand doppler estimation statistics［J］．IEEE Trans．Aerosp．Eleetron．Syst，2011，9：151—165．

［3］ Kay S．A fast and accurate single frequency estimator［J］．JEEE Trans．Acoust Speech Signal Process，2010，37（12）：1987—1990．

［4］ Li Shiyong，Li Panchi．Quantum genetic algorithm based on real encoding and gradient information of object function［J］．Journal of Harbin Institute of Technology，2010，38（8）：1216—1218．

［5］ 杨贤军．基于模糊理论的智能PID控制器设计［J］．制造业自动化，2013，35（2）：115—118．Yang Xianjun．The design of intelligent PID controller based on fuzzy theory［J］．Manufacturing Automation，2013，35（2）：115—118．

［6］ 任伟建，杜红嘉，郇启亮．神经网络PID控制器在油田标定间上的应用［J］．大庆石油学院学报，2001，25（2）：27—30．Ren Weijian，Du Hongjia，Huan Qiliang．Application of neural network PID controller to the calibration shop of oilfield［J］．Journal of Daqing Petroleum Institute，2001，25（2）：27—30．

［7］ 郑雪梅，姜成国，周广铭．模糊PID控制器结构［J］．大庆石油学院学报，2000，24（3）：46—51．Zheng Xuemei，Jiang Chengguo，Zhou Guangming．Structure of fuzzy PID controllers［J］．Journal of Daqing Petroleum Institute，2000，24（3）：46—51．

［8］ 姜立强，刘光斌，郭铮．基于差分进化算法的PID参数整定［J］．计算机仿真，2012，26（6）：204—208．Jiang Liqiang，Liu Guangbin，Guo Zheng．Parameter tuning of PID controller based on differential evolution［J］．Computer Simula—tion，2012，26（6）：204—208．

［9］ Souriee A，Plantier G，Saumet J L．Two—dimensional frequency estimation using autocorrelation phase fitting［C］．Hongkong：Proc．Int．Conf．Acoustics，Speech，Signal Processing（ICASSP），2011：445—448．

［10］ 唐玉兰，徐明亮．粒子群算法在PID控制器参数整定中的研究与应［J］．计算机工程与应用，2012，25（9）：45—49．Tang Yulan，Xu Mingliang．Research and application of particle swarm optimization in parameter tuning on PID controller［J］．Com—puter Engineering and Applications，2012，25（9）：45—49．

［11］ 邓丽，蒋婧，费敏锐．基于免疫粒子群算法的PID参数整定与自适应［J］．自动化仪表，2013，34（2）：65—71．Deng Li，Jiang Jing，Fei Minrui．PID parameters tuning and adaptation based on immunity particle swarm optimization［J］．Process Automation Instrumentation，2013，34（2）：65—71．

［12］ 霍延军．基于量子粒子群算法的PID参数自整定方法［J］．微电子学与计算机，2012，29（10）：194—197．Huo Yanjun．Auto—tuning of optimum PID controller parameters based on quantum—behaved particle swarm optimization［J］．Microe—lectronics ＆Computer，2012，29（10）：194—197．

［13］ 曾现峰，李波，侯春．基于改进微粒群优化的PID控制器参数整定［J］．工业控制与应用，2012，26（10）：24—28．Zeng Xianfeng，Li Bo，Hou Chun．Tuning of PID controller parameters based on improved particle swarmoptimization［J］．Techniques of Automation and Applications，2012，26（10）：24—28．

［14］ 高峰．基于小波网络的PID控制器参数整定研究［J］．洛阳理工学院学报，2012，22（1）：60—64．Gao Feng．The tuning method of PID parameters based on WNN［J］．Journal of Luoyang Institute of Science and Technology，2012，22（1）：60—64．

［15］ 王芳，谢克明，刘建霞．基于群体智能的思维进化算法设计［J］．控制与决策，2010，25（1）：145—148．Wang Fang，Xie Keming，Liu Jianxia．Swarm intelligence based MEA design［J］．Control and Decision，2010，25（1）：145—148．

［16］ 付伟，杨先一，柴毅，等．网络控制系统的自整定PID控制器设计［J］．控制与决策，2011，27（8）：146—149．Fu Wei，Yang Xianyi，Chai Yi，et al．Design of self—adjusting PID controller for networked control systems［J］．Control and Deci—sion，2012，27（8）：1231—1236．

［17］ 李洁，柴天佑，宫经宽．基于交叉熵算法的PID控制器设计［J］．控制与决策，2011，26（5）：794—796．Li Jie，Chai Tianyou，Gong Jingkuan．Design of PID controller using cross entropy method［J］．Control and Decision，2011，26（5）：794—796．

TP301

A

2095—4107（2013）04—0075—07

DOI 10．3969／j．issn．2095—4107．2013．04．011

2013—04—02；编辑：任志平

国家自然科学基金青年科学基金项目（61100103）；黑龙江省自然科学基金面上项目（F201219）

魏连锁（1975—），男，硕士，讲师，主要从事人工智能与算法方面的研究．