天然气凝析液长距离管道稳态水力热力计算

王 智，宫 敬，尹铁男，吴长春

（中国石油大学（北京）城市油气输配技术北京市重点实验室，北京 102249）

天然气凝析液长距离管道稳态水力热力计算

王 智，宫 敬，尹铁男，吴长春

（中国石油大学（北京）城市油气输配技术北京市重点实验室，北京 102249）

针对长距离天然气凝析液管道输送相间质量、动量和能量传递等问题，基于多相流及化工热力学理论，建立稳态条件下水力热力计算方法．结合两相管流的机理模型与相平衡计算，采用简化的能量方程，耦合水力热力，通过逐段循环迭代确定压力、温度、持液率等．通过闪蒸计算，得到指定温度、压力的气、液组成．利用简化的Barnea流型判别方法判断流型，由各流型下的流动机理模型计算相应的摩阻，持液率及气、液相速度．管道模拟结果表明：文中求解方法稳定可靠；精度与现场数据接近，能够满足大型管道工程需要．

两相流；水力热力计算；稳态计算；天然气凝析液；管道流动

0 引言

常规油气输送在深海、沙漠腹地等地理环境复杂地区成本较高，因此经济性好的气、液混输技术得到日益广泛的应用．为了保证输送安全运行，管道设计合理，需要以准确的管道流动模拟作为基础．人们主要以空气、水体系为研究对象，而在混输管道、石油化工、油路系统中大多接触到的是油气流体，其特点是组分多、相态变化复杂．对由相变导致的相间质量、动量和能量传递等问题，天然气凝析液管道的流动参数计算尚不成熟．

早期的稳态计算多采用相关式模型，常用的方法有Eaton相关式方法［1］、Oliemans相关式方法［2］及Beggs—Brill相关式方法［3］．当管流条件适用时相关式模型比较准确，但油气两相管流影响因素较多，纯经验相关式的计算精度和使用范围受到限制，由此产生稳态机理模型，如Wallis G B提出分散气泡流的均质无滑脱模型［4］；Taitel Y等提出分离流的机理模型［5］；Xiao J J等提出综合机理模型，包括流型判定模型与各流型下的机理模型［6］．流型不同，气、液两相流动的相互作用机理不同．Barnea D A综合流型方面研究成果，提出可适用于各种倾角的流型判别模型［7］，该模型为目前计算结果较好的流型判别模型．Taitel Y等［8］认为在石油工业中，瞬态相对较慢，应该采用准静态动量方程和瞬态连续方程得到简化的模型，并且设计相应的求解方法．IFP、TOTAL和ELF AQUITAINE合作开发基于漂移流模型的气、液两相管流瞬态模拟软件TACITE．Tulsa大学多相流课题组也在无压波模型的基础上推出多相流软件TUFFP．挪威IFE和SINTEF等机构联合开发基于双流体模型软件OLGA，并得到行业内认可．

在稳态流动的前提条件下，笔者针对天然气凝析液以两相管流的机理模型为主体，结合相平衡计算、流型判断模型及两相管流相关式方法，耦合相态与水力热力计算，建立天然气凝析液管道稳态条件下的水力热力计算方法，为长距离天然气凝析液输送管路的设计、计算提供简便易行的水力热力计算方法．

1 控制方程及其简化

1．1 基本假设

（1）天然气凝析液为气、液两相流动状态，忽略夹带；（2）一维流动不考虑各参数在管道截面上分布的不均匀性，即截面上压力、持液率、气相速度、液相速度为截面平均值；（3）流动是慢瞬变过程，稳态条件下局部动量平衡，忽略动量方程中的时间项、加速度项及相间的压差［8］．

1．2 连续性方程及动量方程

基于质量守恒和动量守恒，在一维假设条件下，沿管长得到气、液相连续性方程组为

式中：Qg、Ql分别为气、液相体积流量；ρg和ρl分别为气、液相密度；A为管道截面积；L为管道长度；˙mlg为单位管长中液相的蒸发速率，反映液相向气相传递的质量［9］，

其中，G为总质量流量下标；X为气相质量相含率；p为压力；T为管道中气、液混合物的温度；下标T和p分别为温度或压力不变时质量含气率随压力和温度的变化率．

气、液相的联合动量方程［6］：

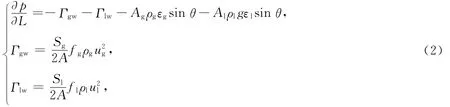
式中：Γgw和Γlw分别为气、液相与管壁的剪切力；Ag和Al分别为气、液相所占管道横截面积；εg和εl分别为气、液截面相分率；θ为管道倾角；Sg、Sl、Si分别为气相、液相和相间湿周；fg和gl分别为气、液相的范宁摩阻系数；ug和ul分别为气、液相速度．

1．3 能量方程简化

在稳态条件下，忽略瞬时项和加速度项的影响，能量方程［10］表示为式中，G为总质量流量；下标hm为单位质量混合物的焓；cpm为气、液混合物的定压比热容，cpm为气、液混合物的汤焦效应系数，为重力加速度；U为气、液两相沿着管壁向环境传热的总传热系数；Te为管道周围环境温度；D0为管道外径．

2 封闭关系及流型判定

基于气、液两相流体模型建立控制方程组，摩阻封闭关系表示气、液相与管壁间的剪切力，气、液相间的剪切力，以及气、液相相平衡关系．

2．1 组分热力学模型

计算时天然气凝析液的组成为已知条件．对于式（1）—（3）中所含有的流体物性参数，利用相对成熟的组分热力学模型得到．采用PR状态方程及范德华单流体混合规则，利用逸度模型，在压力温度一定的条件下进行闪蒸的相平衡计算，得到气、液两相密度、焓、黏度及表面张力、汤焦效应系数等热力学参数［11］．

2．2 流型判定

流型判定是气、液两相管流稳态计算的重要基础，不仅直接影响相关式模型中压降与持液率的计算，也是剪切力计算的重要依据．

在实际模拟程序中复杂的流型划分并未提供给计算精度，各种商业软件在模拟方法设计中都根据气、液相间作用的本质对流型进行大幅简化［12］．Barnea D A建立适用于所有管径、所有倾角的流型判别方法．根据Barnea流型判别准则［13］简化流型判定［14］，针对天然气凝析液管道中气相占主导的特点，将流型划分为泡状流、分层流、环状流和间歇流．

2．3 湿周与摩阻封闭关系

2．3．1 流型与湿周关系

根据文献［15］，湿周与流型的关系见表1．其中：hl为液位高度；Lu为段塞单元长度；Lf、Ls分别为液膜、液塞长度；εg、εl分别为气、液相的相含率；φ为液膜所对应的半圆心角，

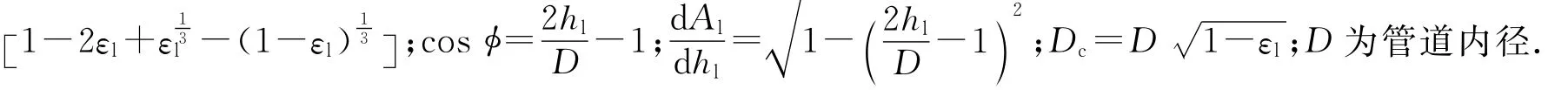
表1 流型湿周关系Table 1 Flow—pattern and wetted perimeter relationship

分别按泡状流和分层流计算段塞流的液塞区与液膜区，然后基于各段长度加权平均，求解速度界面处段塞单元的平均剪切力．液塞长度采用斯科特（Scott）关系式［15］计算，液膜区泰勒气泡的运动速度采用本迪克森（Bendiksen）关系式［15］计算．

2．3．2 范宁摩阻系数

（1）气、液相与壁面：层流采用Hagen—Poiseille方程［16］计算；湍流采用Colebrook—White隐式方程［17］计算．

（2）气、液相间：分层流采用Andritsos—Hanratty相关式［17］计算；环状流采用Wallis［4］相关式计算．

泡状流可视为均相流动，两相间没有滑脱，因此不计相间阻力．对于气、液相与壁面的范宁摩阻系数，在层流时采用Hagen—Poiseille方程计算；在湍流时采用Colebrook—White隐式方程计算，方程中相关参数使用气、液混合物的平均值．

段塞流的范宁摩阻系数为液膜段和液塞段范宁摩阻在液塞单元长度上的加权平均，液膜段按照分层流计算，液塞段按照泡状流计算．

3 管段划分及控制方程离散

首先将管道分为若干长度管段，每个管段内管道具有同一倾角和外部环境；然后在每一管段内再将它等分为长度近似的微元管段［18］．文中划分约为1．0km的管段微元，最长不超过1．5km．

任选第i个管段，对应的上游节点为i—1和i（见图1），得到2个节点的离散控制方程［11］．

气相连续方程为

图1 管道节点划分示意Fig．1 Schematic diagram of discretization

液相连续方程为

联合动量方程为能量方程为

4 计算方法

针对稳态问题，管道各截面处的质量流量相等，结合闪蒸计算从入口边界推算下游相邻节点的流速等变量．因此，采用向下游逐点求解的方法，从入口开始向下游推算，一直达到管道出口［19］（见图2）．

图2 稳态水力热力计算流程Fig．2 Algorithm flow chart of Steady—state hydraulic thermodynamic

（1）将整条管道划分为若干管段．

（2）在管段入口温度压力条件下进行闪蒸，得到两相的物性、相含率、折算速度等参数，根据物性参数，利用B—B［16］（Beggers—Brill）方法计算下一节点的各相流速、压力初值．

（3）利用离散形式的简化能量方程求解下一节点温度值．

（4）求解该管段的温度、压力平均值，并通过闪蒸计算得到该段的平均两相的物性参数．

（5）根据速度初值，两相物性等参数判断流型．

（6）根据各流型下的机理模型计算该管段的剪切力、持液率及下一节点的压力、折算速度．

（7）将上一步得到的压力与该节点压力初值比较，如满足精度要求，返回步骤（2）计算下一个管段；反之，返回步骤（3），将得到的压力带入简化的能量方程，继续循环，直至满足精度要求．

对于步骤（6），在流型为分层流、段塞流、环状流时，通过2个子步骤完成，首先求解各个流型下的平衡方程［16］；其次求解联合动量方程，得到下一节点的压力．对于平衡方程，根据持液率、湿周、流型、流速及摩阻之间的关系，可以转换为持液率的隐式方程，通过二分法或者牛顿法求解［20］．在泡状流时，直接利用混合物的参数，按照单相流动的方法求解压降．

5 模拟计算

5．1 组分及基础数据

为验证算法的适用性和精确程度，选择5条天然气凝析液管道进行计算．管道为油气田地面集输管道，用P1—P5表示，均为起伏管道，倾角为0°～15°，全长分别为74．0、50．0、43．4、6．8和4．3km，组分和基础参数见表2和表3．

表2 P1—P5管道组分摩尔分数Table 2 Mixture component in pipeline P1—P5 %

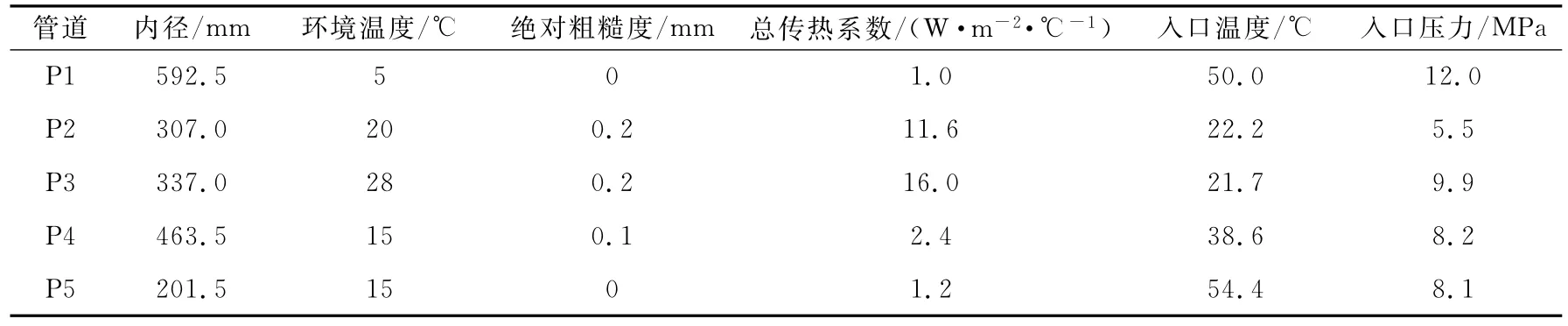
表3 P1—P5管道基础参数Table 3 Basic parameter in pipeline P1—P5

5．2 实例验证

5条管道有实际运行数据，为现场SCADA系统实时采集所得到的数据平均值．对比现场与计算数据可以看出，计算值和实测值绝对误差上，压降相差0．3～0．8MPa，温度相差2～7℃不等；相对误差上，压降为3%～11%，温降为7%～14%（见图4）．产生差异的原因：对于大型管道，基础参数相对宏观和粗略，如P2管道实测入口温度为21．7℃，出口温度为29．6℃，而提供的环境温度为28℃；另外，文中采用各类文献中较认可的小口径多相实验环道的经验关系，与实际大口径管道相比存在一定偏差［21］．总体上，对于大型天然气凝析液管道工程，精度可以满足实践需要．

表4 现场与计算数据对比结果Table 4 Comparison result between calculation and field

根据压力、温度及持液率的沿程分布，以P1管道为例，计算结果表明，流体的温度随着输送距离延伸不断下降，在管道的上游下降较快，随着管道延伸温降趋于缓和（见图3）．这是流体不断与周围介质换热造成的，流体最初进入管道时流体温度与周围环境温度相差较大，换热相对剧烈，因此出现较大的温降；随着管道流动距离的延伸，流体与环境的温差不断减小，换热趋于缓和，因此管道下游的温降较上游的要小．

根据管道温度压力分布，由相平衡理论，整条管道的压力温度分布应处于相图中的反凝析区，因此无论压力还是温度降低都使液相含量增加．根据持液率分布，尽管局部受到地形影响（表现为上坡段液相积累，下坡段液相加速）（见图3），总体上持液率增加．另外，由于温降总体上比较平稳，所以液体的析出速率总体变化不大；持液率的变化更多地受到地形影响．

图3 P1管道流动参数沿程分布Fig．3 Flow parameter distribution in pipeline P1

6 结束语

在多相流动及热力学理论基础上，提出一种稳态条件下的天然气凝析液长距离管道输送的水力热力计算方法，引入简化的Barnea流型判别方法，使各种流型下的机理模型统一于流型判断中；在两相管流机理模型基础上，结合热力计算及相平衡计算，采用相关式方法的部分成果为计算提供初值和部分经验关系．

在对天然气凝析液混输管道进行水力热力计算时，计算结果在各参数的沿线趋势上符合基本物理规律，数值与现场实时数据的平均值接近．总体上，该算法简便易行，能够满足大型管道工程精度要求．

［1］ Eaton B A，Andrews D E，Knowles C R，et al．The prediction of flow patterns，liquid holdup and pressure losses occurring during continuous two—phase in horizontal pipelines［J］．J．P．T．，1967，（6）：815—923．

［2］ Oliemans R V A，Pots B F M，Trompe N．Modeling of annular dispersed two—phase flow in vertical pipes［J］．Intl．J．Multiphase Flow，1986，12（5）：711—732．

［3］ Beggs H D，Brill J P．A study of two phase flow in inclined pipes［J］．J．P．T．，1973（5）：607—617．

［4］ Wallis G B．One dimension two—phase flow［M］．New York：McGraw—hill，1969．

［5］ Taitel Y，Lee N，Dukler A E．Transient gas—liquid flow in horizontal pipes：modeling the flow pattern transitions［J］．AIChE Jour—nal，1978，24（5）：920—934．

［6］ Xiao J J，Shoham O，Brill J P．A comprehensive mechanistic model for two—phase flow in pipelines［C］．New Orleans：The 65th An—nual Technical Conference and Exhibition of the Society of Engineers，SPE 20631，1990．

［7］ Barnea D A．Unified model for predicting flow pattern transitions for the whole range of pipe inclinations［J］．Intl．J．Multiphase Flow，1987，13（1）：1—12．

［8］ Taitel Y，Barnea D．Simplified transient simulation of two phase flow using quasi—equilibrium momentum balance［J］．Int．J．Multi—phase Flow 1997，23（3）：493—501．

［9］ 李玉星．湿天然气管道输送工艺计算研究［D］．北京：中国石油大学（北京），1997：9—10．LI Yuxing．Study on wet gas transportation process calculation［D］．Beijing：China University of Petroleum（Beijing），1997：9—10．

［10］ 邓道明．天然气——凝析液混输管流特性模拟研究［D］．北京：中国石油大学（北京），2005：50—82．Deng Daoming．Modeling gas—condensate two—phase flow in pipeline［D］．Beijing：China University of Petroleum（Beijing）：2005：50—82．

［11］ 黄小红，左龙．基于计算方法的地层油注气后相态特征［J］．大庆石油学院学报，2006，30（3）：54—56．Huang Xiaohong，Zuo Long．Phase state characteristic after gas injection into formation oil based on computational method［J］．Journal of Daqing Petroleum Institute，2006，30（3）：54—56．

［12］ Dhulesia H，Lopez D，Aquitaine E．Critical evaluation of mechanistic two—phase flow pipeline and well simulation models［C］．SPE 36611，1996．

［13］ Barnea D．A unified model for predicting flow pattern transitions for the whole range of pipe inclinations［J］．Intl．J．Multiphase Flow，1987，13（1）：1—12．

［14］ 韩洪生，王忠信，杨树人，等．圆管中气、液相流动空隙率数学模型［J］．大庆石油学院学报，2002，26（4）：19—21．Han Hongsheng，Wang Zhongxin，Yang shuren，et al．Mathematical model of void fraction for gas—liquid two—phase flow in pipelines ［J］．Journal of Daqing Petroleum Institute，2002，26（4）：19—21．

［15］ Ovadia Shoham．Mechanistic modeling of gas—liquid two—phase flow in pipes［M］．USA：Society of Petroleum Engineers，2006．

［16］ 陈涛平，张权．高凝油抽油机井井筒压力——温度分布预测［J］．大庆石油学院学报，2011，35（2）：62—67．Chen Taoping，Zhang Quan．Prediction of wellbore pressure and temperature distribution in the pumping wells producing high pour point oil［J］．Journal of Daqing Petroleum Institute，2011，35（2）：62—67．

［17］ Andritsos N，Hanratty T J．Influence of interfacial waves in stratified gas—liquid flows［J］．AIChE J，1987，33（3）：444—454．

［18］ 吴国忠，陈超．埋地管道传热数值模拟网格划分方法［J］．大庆石油学院学报，2005，29（2）：82—84．Wu Gongzhong，Chen Chao．Grid division method for buried pipelines during numerical simulation［J］．Journal of Daqing Petroleum Institute，2005，29（2）：82—84．

［19］ 贾永英，刘扬，刘晓燕，等．含蜡原油管道再启动压力计算［J］．大庆石油学院学报，2008，32（5）：45—54．Jia Yongying，Liu Yang，Liu Xiaoyan，et al．Pressure calculation of the restart of waxy crude oil pipelines［J］．Journal of Daqing Pe—troleum Institute，2008，32（5）：45—47．

［20］ 贾永英，刘扬，王玉洁，等．非牛顿原油层流埋地热油管道沿线温度的确定［J］．大庆石油学院学报，2006，30（6）：51—52．Jia Yongying，Liu Yang，Wang Yujie，et al．Temperature determination of laminar of non—Newtonian crude oil in buried pipelines ［J］．Journal of Daqing Petroleum Institute，2006，30（6）：51—52．

［21］ Bendiksen K H，Malnes D，Moe R，et al．The dynamic two—fluid model OLGA：theory and application［C］．SPE 19451，1991．

TE832

A

2095—4107（2013）04—0060—07

DOI 10．3969／j．issn．2095—4107．2013．04．009

2013—01—17；编辑：张兆虹

国家科技重大专项（2011ZX05026—004—03）

王 智（1982—），男，博士研究生，主要从事多相管流及油气田集输技术方面的研究．