非均匀分段压裂水平井产能计算

郑松青

（中国石化石油勘探开发研究院，北京 100083）

非均匀分段压裂水平井产能计算

郑松青

（中国石化石油勘探开发研究院，北京 100083）

为考虑非均匀分布裂缝对水平井产能的影响，在保角变换的基础上，引入局部坐标系，建立非均匀分段压裂水平井的产能计算模型，考虑裂缝不同长度、不同间距、同水平井呈一定夹角及裂缝间的相互干扰对产能的影响，对红河地区3口分段压裂水平井产能进行计算，并同郎兆新等建立的模型进行对比，结果显示模型具有更小的误差，但对输入参数要求更高．

保角变换；局部坐标系；多段压裂；水平井产能

0 引言

水平井分段压裂是低渗致密油气藏、页岩油气藏、稠油油藏等复杂油气藏高效开发的主要技术手段之一［1—3］．产能计算是水平井分段压裂优化设计的基础．压裂水平井产能计算方法有两类，一是数值模拟方法［4—6］，二是解析、半解析方法［7—19］．在数值模拟方法中，早期一般对裂缝做等效处理［5］，随着PEBI网格的引入，在一定程度上提高裂缝描述和模拟的精度［6］．解析、半解析方法也可分两类，一是非稳态模型［7—9］，二是稳态模型［10—19］．同非稳态模型相比，稳态模型计算简单，应用方便，因而得到更多关注．Norris S O［10］、Rajagopal R［11］、Hegre T M［12］、Guo Boyun［13—14］等通过不同的方式建立计算模型．郎兆新［15］、范子菲［16］、丁一萍［17—18］等也建立一系列模型．其中郎兆新应用位势理论和叠加原理建立的计算模型得到广泛应用．在该模型中，假设裂缝为垂直裂缝、等间距分布、高度等于储层的厚度，且产量相等．宁正福等［19］在此基础上进行改进，考虑裂缝间的相互干扰，但仍然假设裂缝同井筒垂直、等间距分布．受储层条件和工艺水平的影响，这些假设过于理想化．

笔者在保角变换的基础上，引入局部坐标系，建立考虑裂缝非均匀分布的水平井产能计算模型．

1 单条裂缝在平面上的势分布

单条裂缝的势分布函数是分段压裂水平井产能计算的基础．对于有限长度裂缝的势分布函数，郎兆新等并未给出推导过程［15］，程林松利用保角变换研究势的分布函数，但在后续推导中，将椭圆等势线简化为圆形等势线［20］．文中采用保角变换，重新对其进行推导．假设一条裂缝长度为2L，压开整个储层，忽略裂缝内部的压力损失，将三维流动简化为二维流动．裂缝在Z平面坐标系中的位置见图1．

采用保角变换的方法研究其势分布，取变换函数，即

式中：z＝x+i y，Z为平面上一点；x＝u+i v；W为平面上一点．

通过保角变换，将Z平面上半平面变换为W 平面上带宽为π的右边无限大平面，将Z平面下半平面变换为W 平面上带宽为π的左边无限大平面，将长度为2L的裂缝变换为宽度为π的排液坑道．于是，Z平面上向裂缝的流动经过变换变成W 平面上的坑道流（见图2，Φ为势分布）．坑道流势分布简单，可据此解决裂缝流动的问题．

图1 裂缝分布示意Fig．1 Diagram of a fracture in Z plane

图2 裂缝流动保角变换示意Fig．2 Diagram of conformal transformation

根据双曲函数的性质，对式（1）实部和虚部分离后，可得

根据式（2），可得u同x，y的关系为

如果裂缝的产量为q，储层厚度为h，对于W 平面上的坑道流，势的分布函数Ф为

将式（3）代入式（4），可得单条裂缝在Z平面上势的分布为

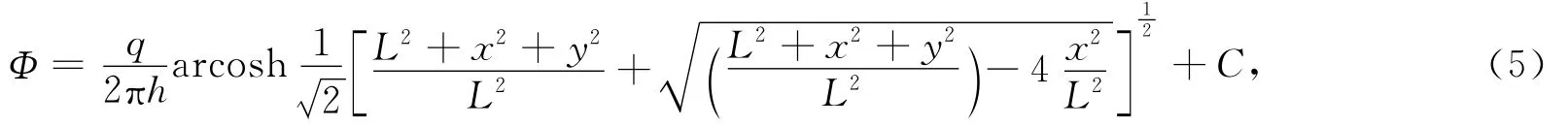
式中：（x，y），（u，v）分别为Z平面和W平面上点的坐标；C为常数．

式（5）势函数假设裂缝中点在坐标原点，裂缝位于x轴．如果裂缝的中点在（x0，y0），且同y轴夹角为θ，就不能直接使用式（5）．为解决这个问题，引入局部坐标系（见图3），在局部坐标系下变量为（x′，y′）满足式，根据全局坐标系同局部坐标系的关系，可得平面上任一条裂缝的势分布为

图3 任意位置裂缝局部坐标系与全局坐标系关系示意Fig．3 Diagram of local and global coordinate system

2 产能计算模型

一口水平井压裂多条裂缝，不考虑未压裂区域水平井产能，多条裂缝产能可通过势的叠加原理求得．根据势的叠加原理，如果存在N条裂缝，空间某点（x，y）的势为

式中：x′i＝（x—xi0）sinθi—（y—yi0）cosθi；y′i＝（x—xi0）cosθi—（y—yi0）sinθi；qi为第i条裂缝的产量；（xi0，yi0）为第i条裂缝的中点坐标；θi为第i条裂缝同y轴（水平井）的夹角；Li为第i条裂缝的半长．

令

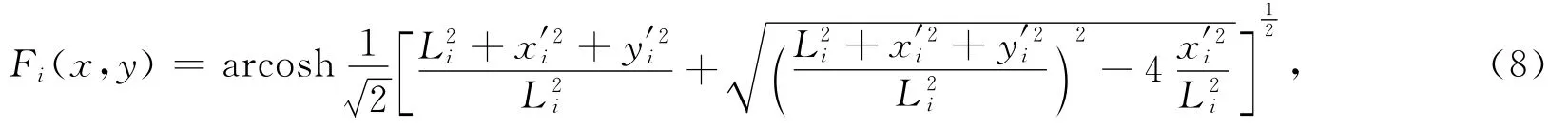
将式（7）简化为

假设第j条裂缝同水平井井筒交点坐标为（0，yj），该处的压力为井底流压pwf，在边界（xe，ye）处压力为pe．根据势同压力的关系，有

将式（9）代入式（10），可得

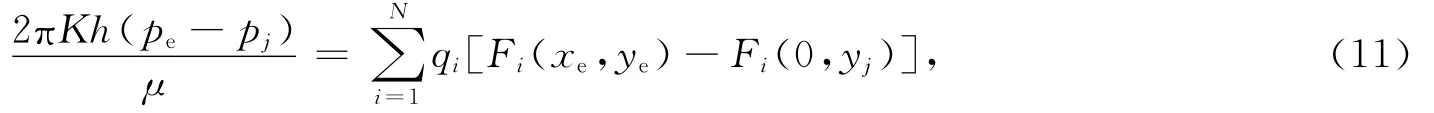
式中：μ为原油黏度；K为储层渗透率；pj为第j条裂缝的压力（井底流压）．

则水平井的产能Q为

3 计算实例

分别利用文中建立的非均匀模型和郎兆新等建立的模型，计算红河油田37井区3口分段压裂水平井产能，并与实际产量进行对比（见表1）．其中HH37P24井的基本参数见表2～3．

表1 2种模型计算结果与实际结果对比Table 1 2Results comparison between calculation and real data t·d—1

表2 HH37P24井基本参数Table 2 Well parameters of HH37P24well

表3 HH37P24井压裂参数Table 3 Fractures parameters of HH37P24well

由表3可知，受到地应力及施工工艺、地层物性等影响，压裂裂缝同水平井完全垂直，长度一致是很困难的．文中非均匀模型考虑裂缝同水平井夹角、裂缝长度不一致等因素影响，得出的结果同实际相比存在较大误差，但比等效模型结果误差要小．主要原因是裂缝间存在干扰，裂缝长度、相对位置、间距等不同，干扰程度不同，整口井的产能也会出现差异．

同郎兆新等建立的模型相比，文中模型虽然误差较小，但对输入参数要求更高，这些参数在现场获取相对困难．

4 结论

（1）在保角变换的基础上，引入局部坐标系，推导非均匀分段压裂水平井产能公式．该公式考虑裂缝不等长、非均匀分布及同水平井不垂直等因素的影响，更符合实际情况．

（2）同郎兆新等建立的模型进行对比，文中模型具有更小误差，但对参数要求更高．

［1］ 刘振宇，刘洋，贺丽艳，等．人工压裂水平井研究综述［J］．大庆石油学院学报，2002，26（4）：96—99．Liu Zhenyu，Liu Yang，He Liyan，et al．Overview of the research of hydraulically fractured horizontal wells［J］．Journal of Daqing Petroleum Institute，2002，26（4）：96—99．

［2］ 王树平，史云清，严谨，等．考虑裂缝干扰的气藏压裂水平井产能预测模型［J］．大庆石油学院学报，2012，36（3）：67—71．Wang Shuping，Shi Yunqing，Yan Jin，et al．A new productivity prediction model of fracturing horizontal well in gas reservoir taking into account the mutual interference between the fracture［J］．Journal of Daqing Petroleum Institute，2012，36（3）：67—71．

［3］ 任俊杰，郭平，王德龙，等．页岩气藏压裂水平井产能模型及影响因素［J］．东北石油大学学报，2012，36（6）：76—81．Ren Junjie，Guo Ping，Wang Delong，et al．Productivity model and influence factors for fracturing horizontal wells in shale gas［J］．Journal of Daqing Petroleum Institute，2012，36（6）：76—81．

［4］ Machiel B，Loyd E，Igor Kuvshinov．The potential of multiple fractured horizontal wells in layered reservoirs［R］．SPE 102633，2006．

［5］ 程林松，皮建，廉培庆，等．裂缝性油藏水平井产能计算方法［J］．计算物理，2011，28（2）：230—236．Cheng Linsong，Pi Jian，Lian Peiqing，et al．A computational method for productivity of horizontal well in naturally fractured reser—voirs［J］．Chinese Journal of Computational Physics，2011，28（2）：230—236．

［6］ 吴军来，刘月田．基于PEBI网格加密的水平井分段压裂模拟［J］．大庆石油学院学报，2010，34（6）：53—57，63．Wu Junlai，Liu Yuetian．Simulation of staged fracturing for horizontal wells based on PEBI grid refinements［J］．Journal of Daqing Petroleum Institute，2010，34（6）：53—57，63．

［7］ 徐严波，齐桃，杨凤波，等．压裂后水平井产能预测新模型［J］．石油学报，2006，27（1）：89—91，96．Xu Yanbo，Qi Tao，Yang Fengbo，et al．New model for productivity test of horizontal well after hydraulic fracturing［J］．Acta Petro—lei Sinica，2008，15（2）：64—68．

［8］ 闪从新，李晓平，秦海菲，等．多裂缝水平井非稳态产能模型及计算方法研究［J］．油气井测试，2008，17（6）：5—7．Shan Congxin，Li Xiaoping，Qin Haifei，et al．Study on the unsteady productivity model of horizontal well with multiple transversal fracture and calculation method［J］．Well Testing，2008，17（6）：5—7．

［9］ 廉培庆，程林松，曹仁义，等．低渗透油藏压裂水平井井筒与油藏耦合的非稳态模型［J］．计算物理，2010，27（2）：203—210．Lian Peiqing，Cheng Linsong，Cao Renyi，et al．A coupling model of low permeability reservoir and fractured horizontal wellbore in nonsteady state［J］．Chinese Journal of Computational Physics，2010，27（2）：203—210．

［10］ Norris S O，Hunt J L，Soliman M Y，et al．Predicting horizontal well performance：A review of current technology［R］．SPE 21793，1991．

［11］ Rajagopal R，Sada D，Joshi．Productivity of multiple drainholes or fractured horizontal wells［R］．SPE 21243，1993．

［12］ Hegre T M，Larsen L．Productivity of multi—fractured horizontal wells［R］．SPE 28845，1994．

［13］ Guo Boyun，Schechter D S．A simple and acturate mathematical model for predicting productivity of multifractured horizontal wells ［R］．SPE 38104，1997．

［14］ Guo Boyun，Yu Xiance．A Simple and accurate mathematical model for predicting productivity of multi—fractured horizontal wells ［R］．SPE 114452，2008．

［15］ 郎兆新，张丽华，程林松．压裂水平井产能研究［J］．石油大学学报：自然科学版，1994，18（2）：43—46．Lang Zhaoxin，Zhang Lihua，Cheng Linsong．Investigation on productivity of fractured horizontal well［J］．Journal of the University of Petroleum：Natural Sciences Edition，1994，18（2）：43—46．

［16］ 范子菲，方宏长．裂缝性油藏水平井稳态解产能公式研究［J］．石油勘探与开发，1996，23（3）：52—57．Fan Zifei，Fang Hongchang．A steady solution formula of horizontal well productivity in a fractured reservoir［J］．Petroleum Explo—ration and Development，1996，23（3）：52—57．

［17］ 丁一萍．压裂水平井产能研究［D］．北京：中国地质大学（北京），2006．Ding Yiping．Analysis for productivity of horizontal fractured well［D］．Beijing：China University of Geosciences（Beijing），2006．

［18］ 丁一萍，王晓冬，邢静，等．一种压裂水平井产能计算方法［J］．特种油气藏，2008，15（2）：64—68．Ding Yiping，Wang Xiaodong，Xing Jing，et al．A method of productivity calculation for fractured horizontal well［J］．Special Oil ＆Gas Reservoirs，2008，15（2）：64—68．

［19］ 宁正福，韩树刚，程林松，等．低渗透油气藏压裂水平井产能计算方法［J］．石油学报，2002（2）：68—71．Ning Zhengfu，Han Shugang，Cheng Linsong，et al．Productivity calculation method of fractured horizontal wells in low permeability oil or gas field［J］．Acta Petrolei Sinica，2002（2）：68—71．

［20］ 程林松．高等渗流力学［M］．北京：石油工业出版社，2011：55—56．Cheng Linsong．Advanced seepage mechanics［M］．Beijing：Petroleum Industry Press，2011：55—56．

TE357．11

A

2095—4107（2013）04—0055—05

DOI 10．3969／j．issn．2095—4107．2013．04．008

2013—07—01；编辑：关开澄

中石化科技攻关项目（P12099）

郑松青（1982—），男，博士，工程师，主要从事油藏工程方面的研究．