螺旋桨飞机近地飞行时的横航向稳定性
2013-03-24周永平
刘 嘉,周永平,张 颖
(1.海军航空工程学院a.接改装训练大队;b.基础实验部,山东烟台264001;2.海军装备部,北京100841)
飞机在着陆过程中要经历平飞、下滑、拉平、飘落等阶段。在着陆拉平段,飞机的飞行高度很低,往往受地面效应影响,同时较低的飞行速度又经常使飞机处于操纵反区[1-2],而且地面突风等气流扰动又给着陆带来了诸多不可预测性[3-4],这就对飞机的稳定性提出了较高要求[5]。
研究表明[6-7],二维机翼的地面效应仅取决于飞行高度与弦长的比值。对于全机而言,其地面效应和飞行高度及机翼的几何尺寸有关。对于常规飞机,地面效应能提高飞机的气动效率,但对于前置螺旋桨飞机,气流将首先经过桨叶,而后流经机翼,其必然会对飞机的气动特性产生影响,若将涡桨发动机换装涡扇发动机,则可以不计滑流影响。基于这种想法,本文将结合算例数据,分析螺旋桨飞机在着陆的最后阶段地面效应及螺旋桨滑流对飞机横航向稳定性的影响。
1 横航向静稳定性
在螺旋桨飞机着陆的最后阶段,飞机飞行高度已不足5 m,此时,地面效应和螺旋桨滑流将共同影响机身上的空气流动特性,从而改变飞机的气动力及静稳定性。
飞行器是否具有航向静稳定性,与平衡点处的力矩系数曲线斜率有关,故可用原点处偏航力矩系数Cnβ作为判据,Cnβ大于0,则飞机为航向静稳定的。同样,横向静稳定性可用原点处滚转力矩系数导数Clβ作为判据,Clβ小于0,则飞机为横向静稳定的。现取迎角α=0时,计算飞机的横航向静稳定性。通常,考虑螺旋桨滑流时,飞机的偏航力矩导数和滚转力矩导数与迎角及螺旋桨滑流的大小有关,它们可表示为:

式(1)、(2)中:TC为发动机拉力系数,一定程度上也表征了螺旋桨引起的滑流大小,因而在本文中用TC代表螺旋桨滑流;ΔCnβ(TC,α)、ΔClβ(TC,α)代表同时存在螺旋桨滑流TC和迎角α 迎角变化时,偏航力矩系数和横向滚转力矩系数增量。
由式(1)、(2)通过插值计算可以求得某型机在不同飞行条件下的横航向静稳定性,如表1所示。

表1螺旋桨飞机的横航向静稳定性Tab.1 Lateral static stability of propeller airplane
1.1 航向静稳定性
由计算可知(见表1),无论是否存在地面效应,随螺旋桨滑流的增加,飞机Cnβ都大于0,并且其绝对值随滑流增加变小。这说明飞机为航向静稳定的,并且其航向静稳定性随螺旋桨滑流增加变差。分析其原因可以发现,偏航力矩主要由侧力和阻力决定,螺旋桨滑流虽然增加了升力系数使侧力增加,却也同时产生了更大的阻力(升阻比随滑流增加而降低[8-9]),因此,螺旋桨滑流将使飞机的航向静稳定性变差。
观察地面效应对飞机航向静稳定性的影响,可以发现无论是否存在螺旋桨滑流地面效应,都将使飞机的航向静稳定性变差(无地效时的Cnβ绝对值大于有地效时的Cnβ绝对值)。这是因为偏航力矩的主要力矩源是由飞机滚转产生的侧力引起的,而地面效应将对飞机的滚转将产生显著的抑制作用[10]。因此,这就造成了偏航恢复力矩的快速消失,致使飞机的航向静稳定性变差。
1.2 横向静稳定性
由表1可见,无论是否存在地面效应,随螺旋桨滑流的增加,该机Clβ均由负值变为正值,这说明,随滑流增加飞机的横向静稳定性变差了。通常,对于横向静稳定性,其主要恢复力矩是上反效应引起的升力差而产生的滚转力矩,其大小应与机翼的升力系数及上反角成正比,在理论上滑流增量确实将导致升力系数增加,使滚转恢复力矩变大[11]。但还应注意到,当存在由滚转引起的侧滑角β时,由螺旋桨滑流引起升力增量ΔLTC的作用点将不再对称(由图1可见d1>d2)。因而当飞机向右滚转后,滑流增量在侧风β 作用下将引起附加的右滚转力矩,使滚转恢复力矩变小。因此,在螺旋桨滑流的作用下,飞机的横向静稳定性变差。
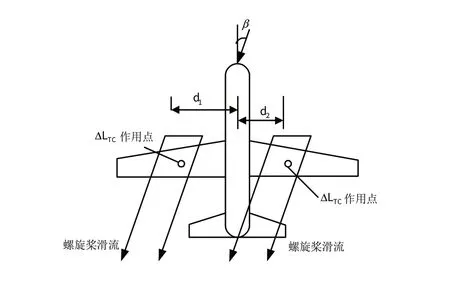
图1 滑流增量对飞机横向静稳定性的影响Fig.1 Influence to lateral static stability of propeller airflow
从表1还可以看出,地面效应将使该机的横向静稳定性增强。这是因为,地面效应提高了飞机的升阻比,升力增加将导致滚转恢复力矩增强。因此,飞机受扰后将很快减小滚转角,使飞机的横向静稳定性增强。
2 横航向动稳定性
运用小扰动法进行动稳定性分析,首先就要求出飞机飞行的基准状态参数。这里假设飞机着陆下滑的基准状态是下滑角恒定(γ=-3.5°)的匀速直线飞行,建立通用的飞机运动方程[11]如下。
2.1 动力学模型
航迹坐标系内飞机的质心运动方程为:
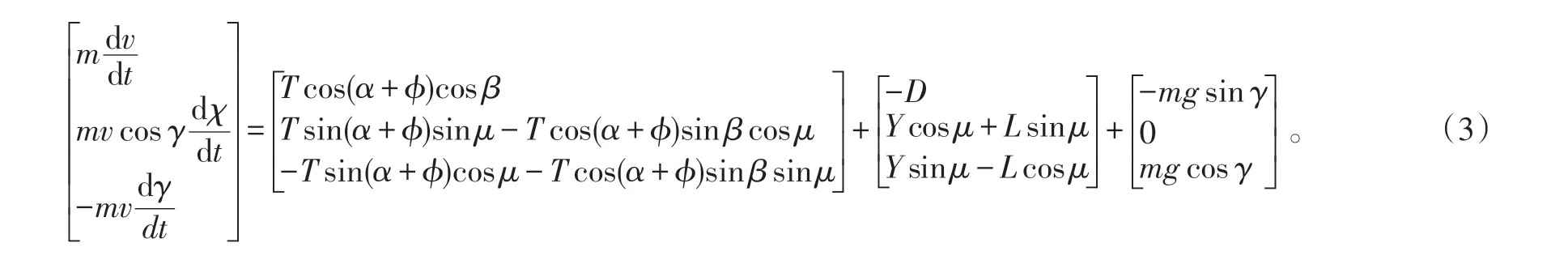
式(3)中:m为飞机质量;v为飞行速度;T为发动机拉力;L、Y、D分别为飞机的升力、侧力和阻力;α为迎角;ϕ为发动机安装角;μ为航迹速度滚转角;χ为航迹方位角;β为侧滑角;γ为航迹倾斜角。
机体坐标系内,飞机的转动动力学方程为:
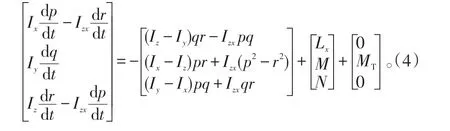
式(4)中:Lx、M、N分别为滚转力矩、俯仰力矩和偏航力矩;p、q、r分别为飞机的滚转角速度、俯仰角速度和偏航角速度;Ix、Iy、Iz分别为飞机相对机体坐标轴的惯性矩;Izx为惯性积;MT为发动机偏心矩引起的俯仰力矩。
由各坐标系之间关系,可以得到补充方程:
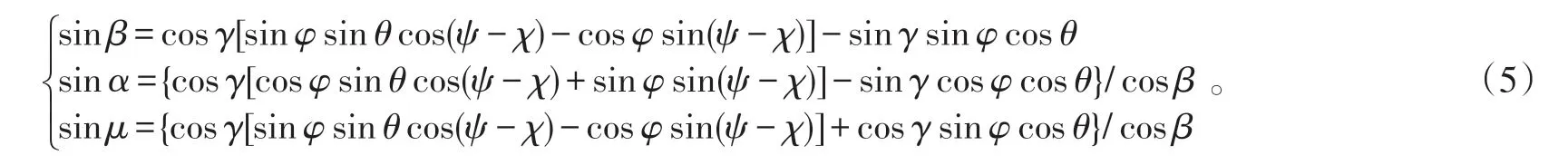
2.2 平衡计算及结果
建立了飞机的运动方程后,就可以通过计算确定飞机飞行的状态参数,如发动机需用拉力,各姿态角及操纵量等。联立方程组(3)~(5),并采用Newton迭代法对其进行求解,得到速度在30~100 m/s 范围内的下滑状态参数如图2~4所示。
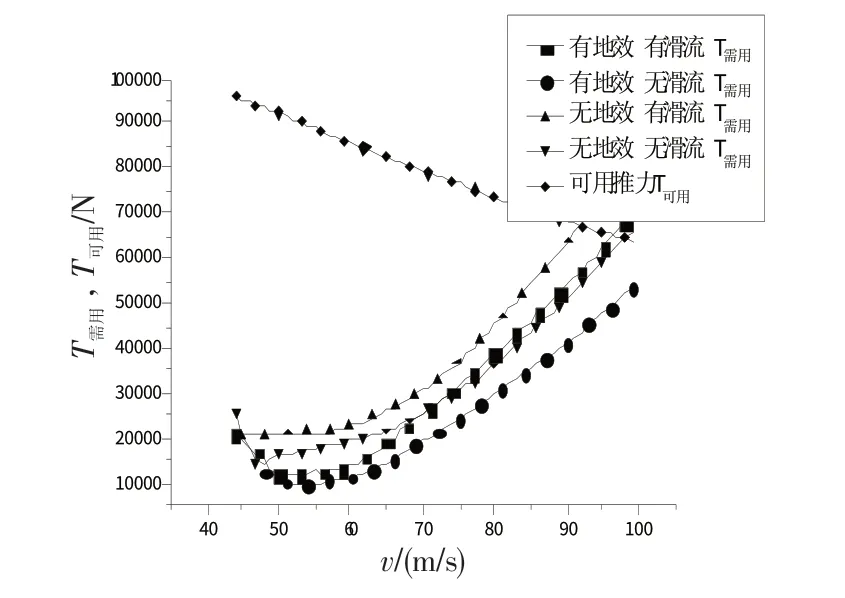
图2 螺旋桨飞机下滑配平需用推力曲线Fig.2 Thrust needed of gliding trim
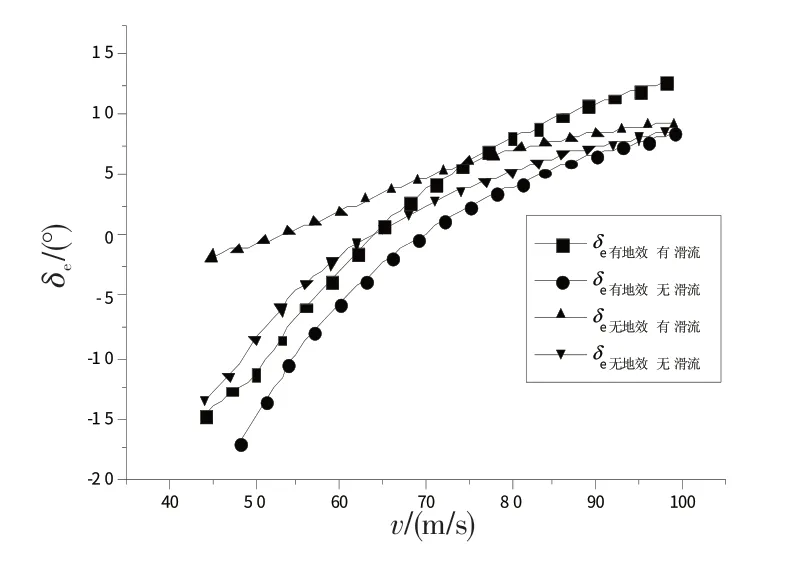
图3 螺旋桨飞机下滑配平所需升降舵偏角Fig.3 Elevator deflection needed of gliding trim
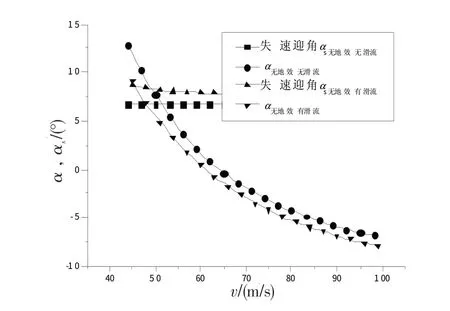
图4 无地效时迎角限制Fig.4 Limits of attack angle without ground-effect in gliding
从图2可以看到,该机着陆下滑的最大速度可由需用拉力与可用拉力的交点来确定(vmax≈90 m/s),而最小可用下滑速度可以由飞机的配平迎角与失速迎角的交点来确定(如图4~5所示vmin≈52 m/s)。从图2~5可见,无论是否存在地面效应及螺旋桨滑流,该型机在速度范围52~90 m/s的范围内均可实现定常直线下滑。

图5 有地效时迎角限制Fig.5 Limits of attack angle with ground-effect in gliding
2.3 横航向动稳定性计算与分析
得到飞机的基准下滑状态参数后,便可以通过小扰动法来进行飞机的动稳定性计算与分析,现将方程线性化,得到飞机的横航向扰动运动方程为:
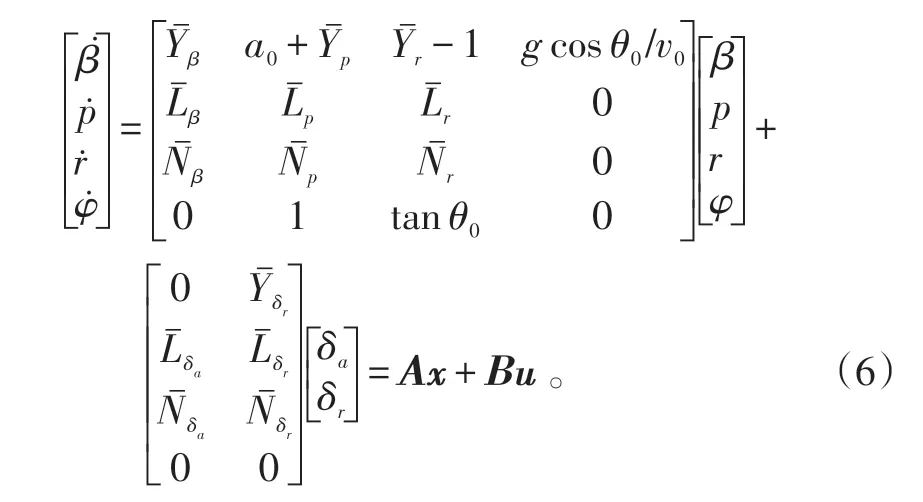
式(6)中:状态矢量x=[β p r φ]T;操纵矢量u=[δaδr]T;δa、δr分别为气动副翼和方向舵偏角;分别为侧滑角β、滚转角速度p、偏航角速度r 引起的无量纲侧力系数;分别为侧滑角β、滚转角速度p、偏航角速度r 引起的无量纲滚转力矩系数;分别为侧滑角β、滚转角速度p、偏航角速度r 引起的无量纲偏航力矩系数。
考虑握杆情况下,只需求得矩阵A的特征值即可判定飞机的横航向动稳定性。经计算,得到该机受地面效应及螺旋桨滑流影响下的横航向特征根轨迹如图6所示。为了使横航向根轨迹显示明显,在此仅显示了53~56 m/s的根轨迹。从图6可以看出,在着陆下滑段,螺旋桨滑流和地面效应对飞机的横航向各模态都将产生影响。为方便评估其对各模态影响,计算该机在50~60 m/s时各模态主要参数如图7~9所示。
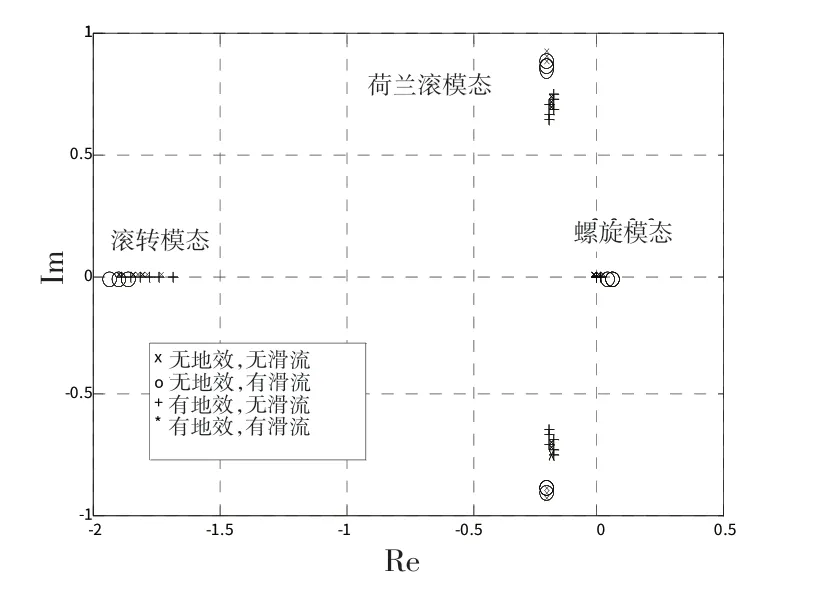
图6 地面效应及螺旋桨滑流影响下的横航向特征根轨迹Fig.6 Lateral root locus in ground-effect and propeller airflow
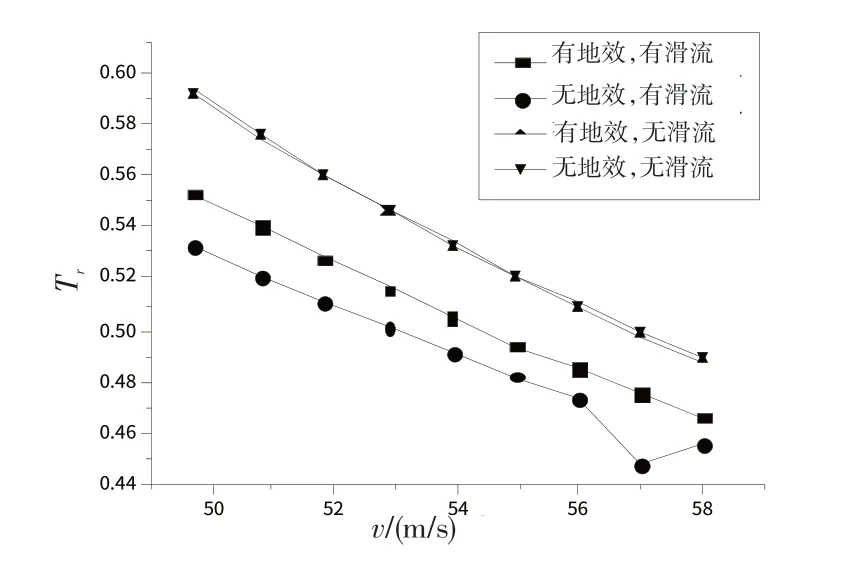
图7 地效及滑流对滚转模态的影响Fig.7 Effecttorollingmodalof ground-effectandpropellerflow
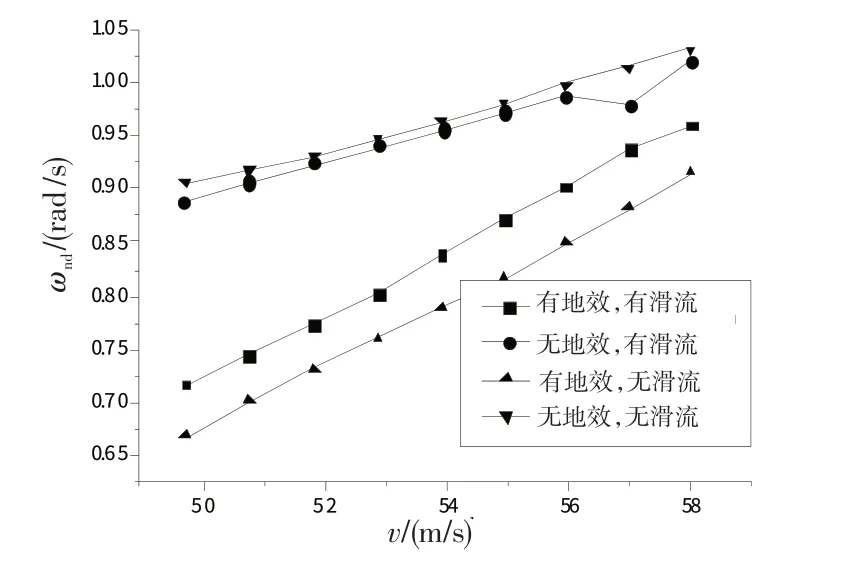
图8 地效及滑流对荷兰滚模态频率影响Fig.8 Effect to frequency of Holland rolling modal in ground-effect and propeller flow
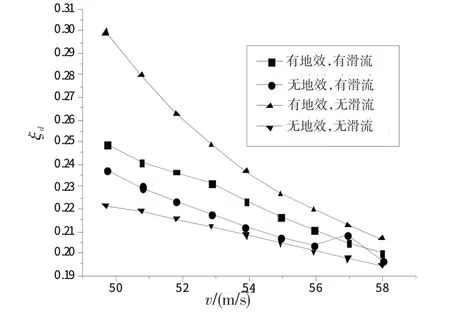
图9 地效及滑流对荷兰滚模态阻尼比的影响Fig.9 Effect to damp of Holland rolling modal in ground-effect and propeller flow
1)滚转模态分析。观察地面效应对滚转模态的影响,由图6可以看出,存在滑流影响时,地面效应将使滚转模态特征根绝对值减小,即有滑流时,地面效应将使滚转模态收敛变慢(见图7),这与文献[10]中结论是一致的。但观察无滑流影响时地效对滚转模态的影响,却结论相反。其原因可能是:①在计算中,由于数据有限,并未采用地效时的滚转阻尼导数Clp,而Clp又是滚转模态的主要影响因素,因而可能导致计算不准确;②在计算地面效应对横航向模态影响时,未考虑滚转角产生力矩系数Clφ带来的影响。
观察螺旋桨滑流对滚转模态的影响,还可以发现,无论是否存在地面效应影响,螺旋桨滑流都将使滚转模态特征根绝对值增加,使滚转模态收敛加快。由文献[11]中滚转模态简化可知,滚转模态的主要影响因素是滚转阻尼导数Clp,而螺旋桨滑流将对Clp产生增量,因而螺旋桨滑流将使滚转模态收敛加快。
2)荷兰滚模态分析。通过研究发现,螺旋桨滑流和地面效应将同时影响荷兰滚模态的频率和阻尼比。
对荷兰滚模态频率的影响。观察地面效应对荷兰滚模态频率的影响,从图8可以发现,无论是否存在滑流影响,在地面效应影响下其频率都要降低。通过文献[11]中荷兰滚模态简化可知,荷兰滚模态的主要恢复力矩源为Nβ>0,其值首先将影响振荡频率,正是由于地面效应致使Cnβ减小(见表1),导致了荷兰滚模态频率降低。
观察螺旋桨滑流对荷兰滚模态频率的影响。可以发现,在地效区内,滑流将使荷兰滚模态频率增加,而非地效区内,滑流将使频率降低。但总体而言,滑流对荷兰滚模态频率影响不大,有滑流影响和无滑流影响的荷兰滚模态频率仅相差不到0.05 rad/s。
对荷兰滚模态阻尼比的影响。分析地面效应及螺旋桨滑流对荷兰滚模态阻尼比的影响,Nr<0 提供了受扰后的主要阻尼力矩源。但Cnr只与迎角变化有关,而不受滑流及地效影响。因此,图9所反映的ξd变化趋势,只是由配平迎角减小造成的,其并不能解释地效及滑流对其造成的影响。可以从物理图景出发,分析地面效应及螺旋桨滑流对荷兰滚模态阻尼比造成的影响。荷兰滚模态是带侧滑的滚转与偏航运动,运动中飞机除受偏航力矩影响外,其还应受到滚转力矩与侧力影响,而侧力又与滚转角φ 及升力系数有关。因此,在阻尼因素当中,受地效及滑流最敏感,而又影响最大的就是滚转力矩Lx。
由图9可见,无论是否存在滑流影响,地面效应都使荷兰滚模态阻尼比增大,这是由于地面效应能明显地抑制滚转运动,致使恢复力矩Lx增大。因此,有地效时的阻尼比要大于无地效时的阻尼比。
观察螺旋桨滑流对荷兰滚模态阻尼比的影响,从图9却发现,其影响在有地效和无地效时影响是不同的,理论上螺旋桨滑流将减小滚转恢复力矩(见1.2),使荷兰滚模态阻尼比减小,但荷兰滚模态为复合运动,其阻尼比除受Nr影响外,Lx中的LβΔβ、LpΔp可起阻尼作用,也可能起激励作用。同时,侧力Y 也将对荷兰滚模态阻尼比产生影响。因此,螺旋桨滑流对荷兰滚模态阻尼比的影响,需综合考虑上述因素的影响。
3)螺旋模态分析。螺旋模态特征根基本都集中在原点附近,为了方便观察分析,现以v=53 m/s时的特征根为例,说明地面效应及滑流对该机螺旋模态的影响。速度v=53 m/s时的螺旋模态特征根如图10所示。

Fig.10 Roots of spiral modal with ground-effect and propeller flow in v=53 m/s
观察地面效应对螺旋模态的影响。从图10可以看出,无论是否存在滑流影响,地面效应都将使螺旋模态特征根左移,稳定性增强。这是因为,螺旋模态主要表现为滚转角φ 和偏航角ψ的缓慢变化。在地面效应影响下,当滚转角φ 改变时,由于地面效应的存在,会额外产生使滚转角减小的滚转力矩,因而螺旋模态稳定性得到了增强。
观察螺旋桨滑流对螺旋模态的影响。从图10可以看出,无地面效应时,螺旋桨滑流使螺旋模态特征根右移,稳定性变差;而有地效时螺旋桨滑流将使螺旋稳定性稍有增强。分析螺旋模态的物理过程,在扰动的后期,其主要表现为带滚转、几乎无侧滑的缓慢的偏航运动,因而其升力的分量就成了偏航力矩的主要来源。而在滑流影响下,飞机的升力系数将提高,这就造成了偏航力矩的增加,增加了螺旋模态的不稳定性。同时,在螺旋桨滑流影响下,飞机阻力也明显升高,升阻比的下降,也使航向更不稳定,因而飞机的螺旋模态也就更加不稳定。但在地效区内,螺旋桨滑流对螺旋模态的影响却有所不同,这仍与地面效应对飞机滚转运动的抑制有关。
3 结论
通过分析地面效应和螺旋桨滑流对横航向稳定性的影响,主要得到以下结论:
1)地面效应和螺旋桨滑流将影响飞机的横航向静稳定性。无论是否存在地面效应,螺旋桨滑流都将使飞机的航向静稳定性和横向静稳定性变差。同时,无论是否存在螺旋桨滑流,地面效应都将使飞机的横向静稳定性增强,航向静稳定性变差。
2)地面效应和螺旋桨滑流还将影响该机的动稳定性。总体而言,无论是否存在地面效应,螺旋桨滑流都将增强滚转模态及荷兰滚模态的稳定性,并同时降低螺旋的稳定性。而无论是否存在螺旋桨滑流,地面效应总体上也都将使飞机的横航向动稳定性增强。
[1]FRED J D,GEORGE E C.A flight evaluation of the factors which influence the selection of landing approach speeds NASA-MEMO-10-6-58A[R].NASA,1958.
[2]王新华,杨一栋.低动压着舰状态下飞机的操纵特性研究[J].飞行力学,2007,25(4):29-32.
WANG XINHUA,YANG YIDONG,ZHU HUA.Research of handling characteristics of aircraft in low dynamic pressure situation[J].Flight Dynamics,2007,25(4):29-32.(in Chinese)
[3]张积亭.飞机垂直和侧向突风载荷分析[D].西安:西北工业大学,2005.
ZHANG JITING.Vertical and crossrange turbulence analyse of aircraft[D].Xi'an:Northwestern Polytechnical University.2005.(in Chinese)
[4]陈勇,金长江.飞机穿越风切变时的地速/空速控制[J].北京航空航天大学学报,2002,28(6):621-624.
CHEN YONG,JIN CHANGJIANG.Ground-speed/airspeed control of airplane during penetration of windshear[J].Journal of Beijing University of Aeronautics and Astronautics,2002,28(6):621-624.(in Chinese)
[5]国防科学技术工业委员会.GJB185-86 有人驾驶飞机(固定翼)飞行品质[S].1986.
COMMITTEE OF NATIONAL DEFENSE SCIENCE TECHNOLOGY INDUSTRY.GJB185-86 Flying qualities of piloted airplanes(fixed wing)[S].1986.(in Chinese)
[6]胡国才.新型倾转旋翼机气动弹性稳定性分析模型[J].海军航空工程学院学报,2006,21(6):601-606.
HU GUOCAI.Mathematical model and formulations of a new tilt-rotor aircraft for aeroelastic stability analysis[J].Journal of Naval Aeronautical and Astronautical University,2006,21(6):601-606.(in Chinese)
[7]蔡国华.地效飞机空气动力特性测量[J].上海航天,2000(3):14-17.
CAI GUOHUA.Measurements of aerodynamic properties of ground-effect plane[J].Aerospace Shanghai,2000(3):14-17.(in Chinese)
[8]胡国才,刘嘉,孙建国.螺旋桨飞机近地飞行时的纵向稳定性[J].海军航空工程学院学报,2009,24(6):601-606.
HU GUOCAI,LIU JIA,SUN JIANGUO.Longitudinal stability of jet-propeller aircraft during low altitude flight[J].Journal of Naval Aeronautical and Astronautical University,2009,24(6):601-606.(in Chinese)
[9]何辉,史爱明,叶正寅.螺旋桨飞机超低空流场数值模拟方法研究[J].工程力学,2009,26(2):222-226.
HE HUI,SHI AIMING,YE ZHENGYIN.Research on numerical simulation method of propeller-driven aircraft flow fields at low altitude[J].Engineering Mechanics,2009,26(2):222-226.(in Chinese)
[10]乐挺,王立新,况龙.农林飞机近地作业飞行的横航向稳定性[J].航空学报,2008,29(4):854-858.
YUE TING,WANG LIXIN,KUANG LONG.Lateral stability of an agriculture aircraft during low-altitude flight operation[J].ACTA Aeronautical et Astronautical SINICA,2008,29(4):854-858.(in Chinese)
[11]方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:24-25,262.
FANG ZHENPING,CHEN WANGCHUN,ZHANG SHUGUANG.Flight dynamics of aerospace aircraft[M].Beijing:Beihang University Press,2005:24-25,262.(in Chinese)
