基于季节时间序列模型对海南旅游人数的预测分析
2013-03-22张雪艳陈传钟胡晓华
张雪艳,陈传钟,胡晓华
(海南师范大学数学与统计学院,海南海口571158)
海南从建省之初的“工、农、贸、旅”并举到后来的“一省两地”战略的提出,再到“大企业进入,大项目带动”的实施,以及随着《国务院关于推进海南国际旅游岛建设发展的若干意见》的发布,海南国际旅游岛建设正式上升为国家战略,极大拓宽了海南的发展视野.能否在这一历史机遇面前实现历史性突破,对于海南至关重要.
时间序列是按时间顺序排列的一组数字序列.利用这组序列,应用数理统计方法加以处理,以预测未来事物的发展.本文是以海南省过夜旅游人数作预测分析.所谓过夜旅游人数是指逗留时间至少超过一夜的旅游人数.旅游人数是考核旅游业的重要指标之一.
1 数学模型
1.1 季节调整模型的建模原理
季节模型[1]是反映具有季节变动规律的时间序列模型.为了更好的观察数据波动的情况一般把传统时间序列的波动归结为四大因素:趋势变动(trend T),季节变动(seasonal S),循环变动(circle C)和不规则变动(irregular I).含有趋势性的时间序列用乘法模型X=TSCI;四大因素之间相互独立时则用加法模型X=T+S+C+I.季节因子(S)反映随时间变化受季节因素的影响程度.季节调整模型的建立主要是对季节因子的测定,其基本步骤是:(1)测定趋势T(采用移动平均法);(2)剔除趋势部分;(3)测定季节因子.
1.2 SARIMA模型的基本原理
SARIMA模型[2]是ARIMA模型的特例,是描述一些明显由季节变化或其他固有因素引起的周期性时间序列的模型.
SARIMA模型是建立在平稳时间序列基础上的模型,通过对原序列的不断平稳化最终建立模型,见式(1):
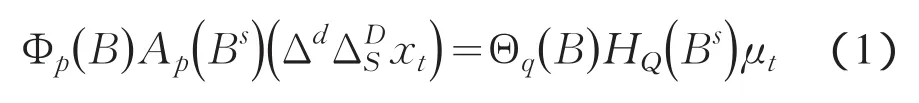
式中B为滞后算子,Φp(B)是非季节p阶自回归算子;Ap(Bs)是季节P阶自回归算子;Θq(B)是非季节q阶移动回归算子;HQ(Bs)是季节Q阶移动回归算子;Δd=(1-B)d是进行d阶逐期差分算子;=(1-Bs)D是D阶季节差分算子;Δdxt是原序列xt经过d阶逐期差分与D阶季节差分后的平稳序列;且
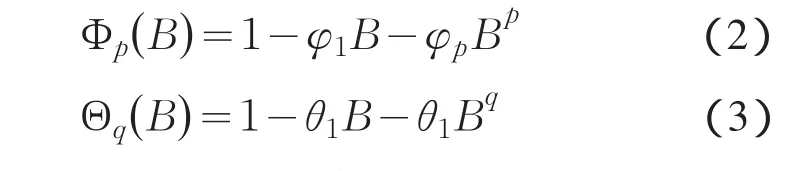
Φp(B) Δdxt表示同一周期内不同周期点的相关关系;Ap(B)则描述不同周期的同一周期点上的相关关系;两者的乘积则刻画了两个因素的共同作用.
SARIMA建模的基本步骤[3]:(1)根据原数列时序图的特性,进行差分与季节差分把原序列xt变成一个平稳的时间序列yt,然后进行平稳性的单位根与相关图检验最终确定d,D;(2)通过对相关图在S周期处的自相关与偏自相关系数值,确定P,Q的值;并通过相关图的拖尾性与截尾性来判定p,q的值;(3)对原序列xt建立
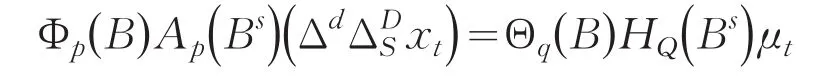
模型;(4)进行模型的参数估计与适应性检验:(a)由差分序列的适当自相关与偏自相值求得模型的初始估计值,并将这些估计值作为最小二乘估计的初始值,对模型参数进行最小二乘估计.(b)对估计得到的暂定模型进行适应性检验,若不接受暂定模型则表明不是最优模型,可根据检验所提供的有关信息改进模型,重新拟合改进模型,并对其进行适应性检验,直到得到最优模型为止;(5)根据(4)建立的方程模型使用Eviews6.0软件中的Forecast功能对其进行预测,并估计其值误差的大小来判定最终预测值.
2 应用实例
2.1 季节调整模型的建立
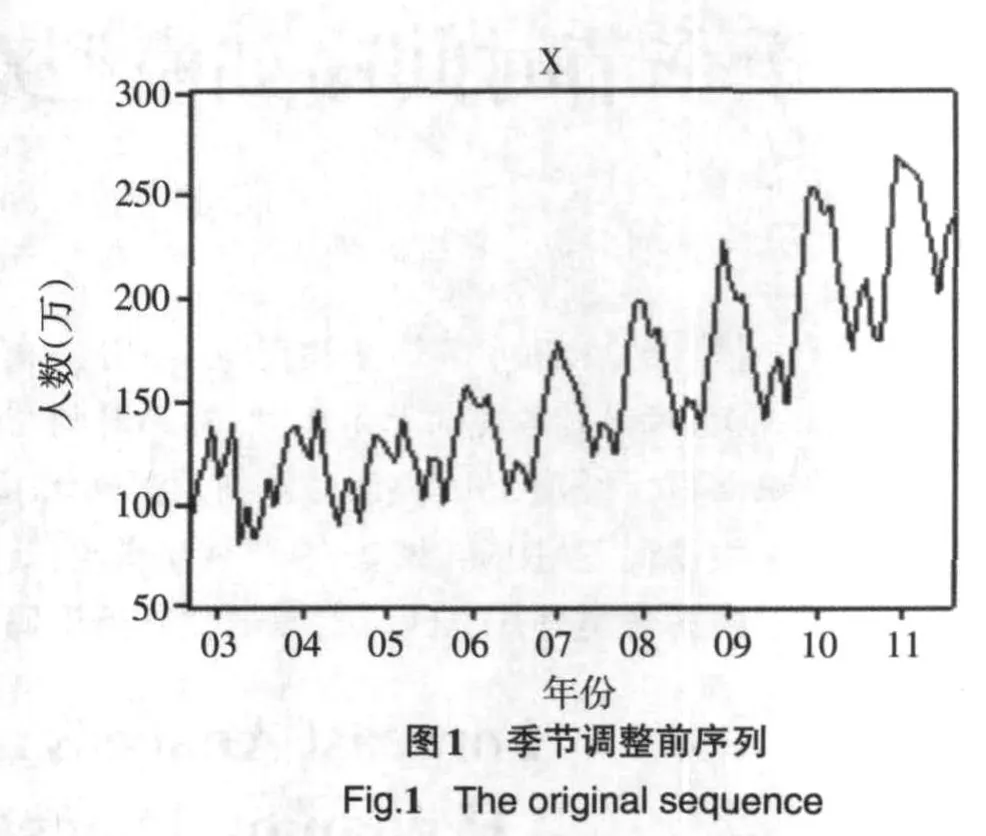
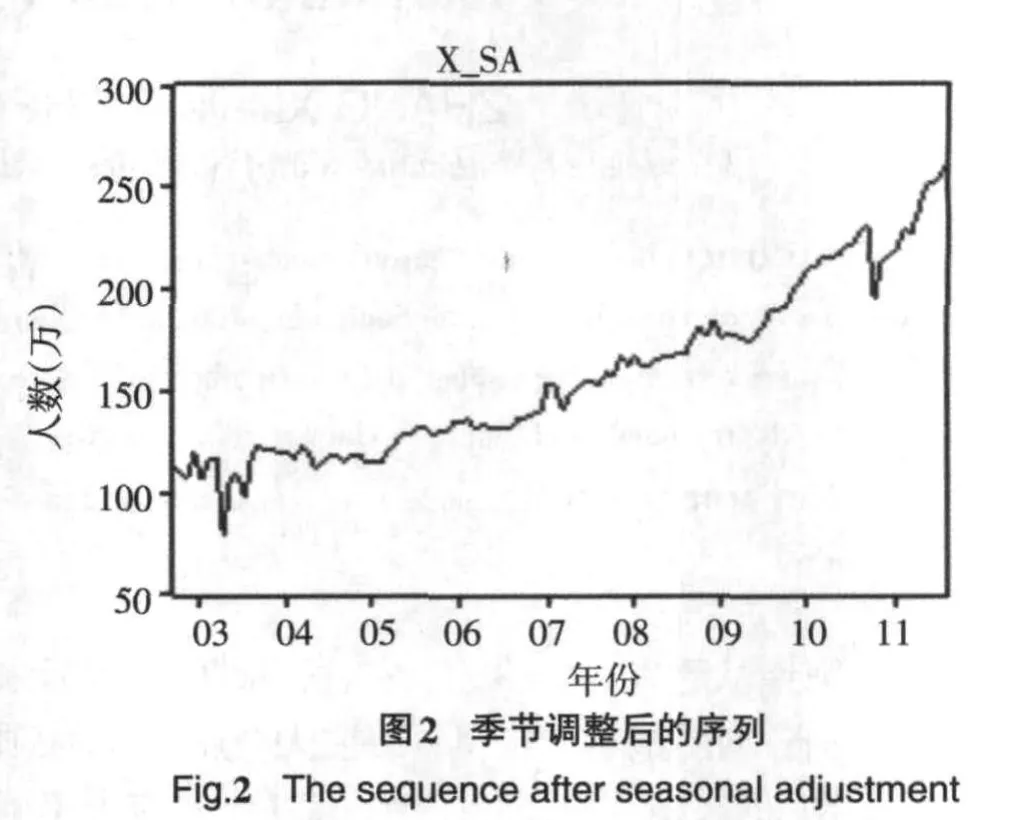
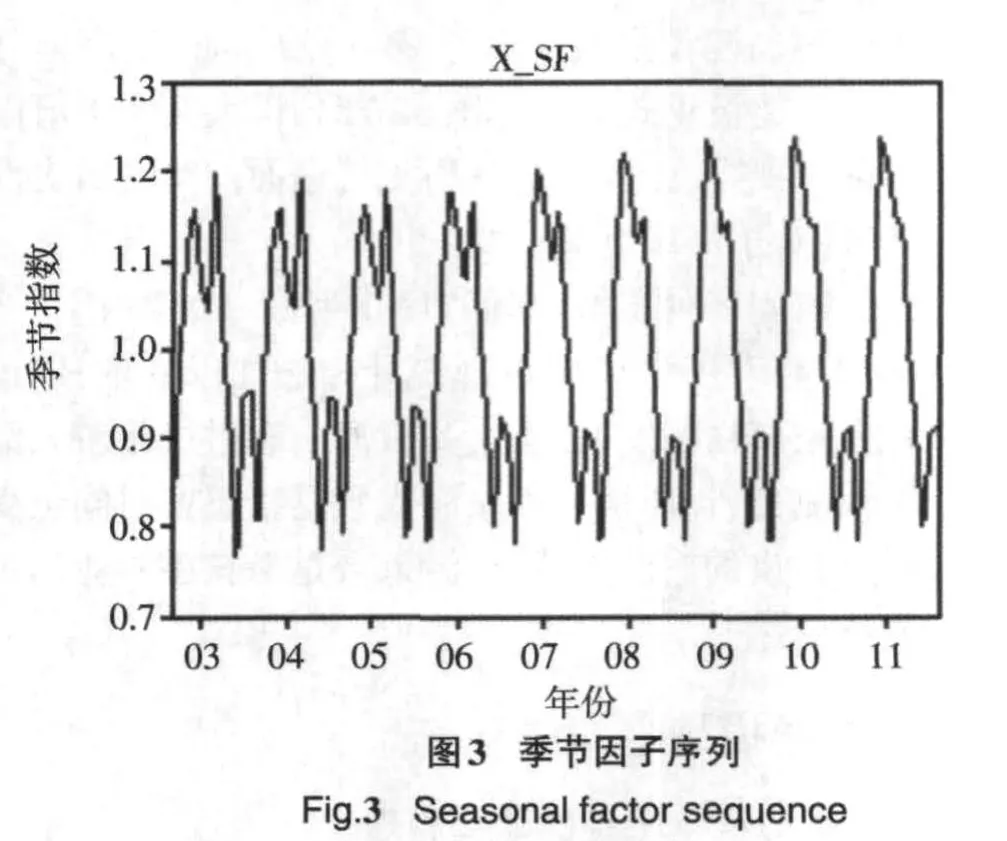
通过使用计量经济学软件Eviews6.0[4]对附表1的数据进行季节调整,所得相关图形见图1~图5.
由图1~图5看出,该序列有明显的规律性.因此可以建立如下的乘积预测模型,见式(4):

其中f(t)为模型的趋势部分,si为季节指数.
通过对季节调整后的序列X_SA进行试拟合f(t)模型,所得的相关参数值见表1.
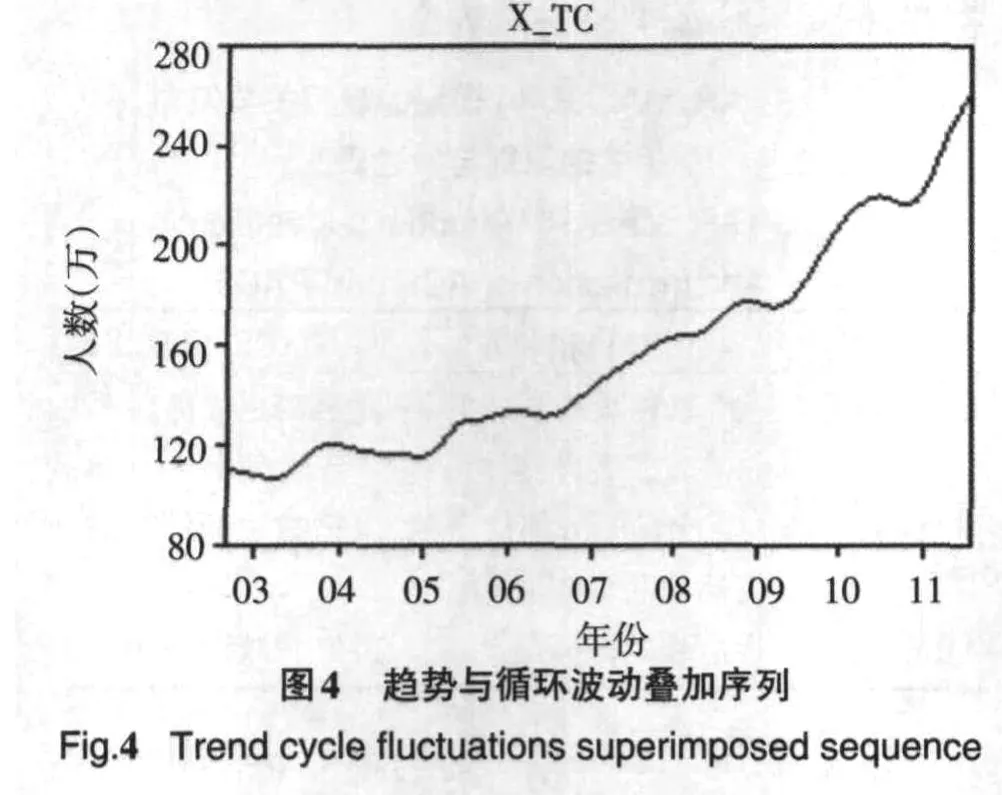
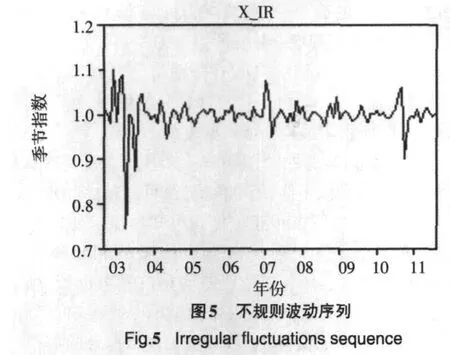
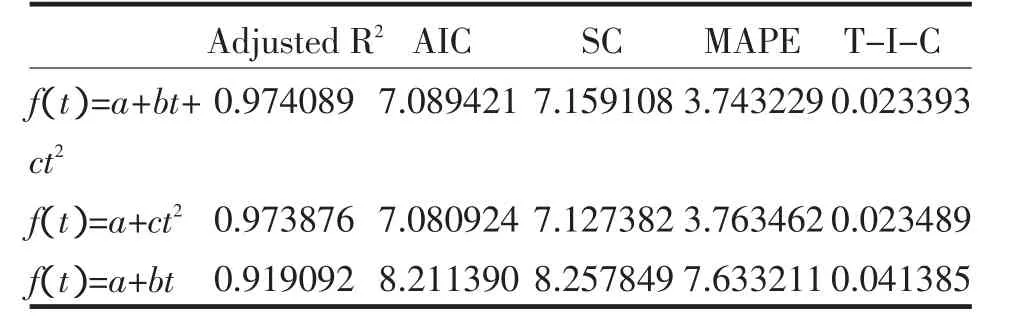
表1 相关参数值Tab.1 The relevant parameter value
根据数据调整后的样本决定系数(Adjusted R2)、AIC准则与SC准则、预测时的平均绝对百分误差(Mean Abs.percent Error简记MAPE)和希尔不等系数(T heil Inequality coefficient简记T-I-C),确定趋势模型为式(5):
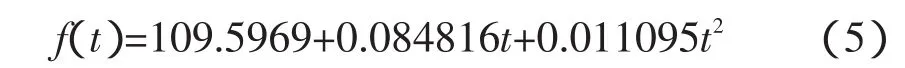
所建立的预测模型为式(6):
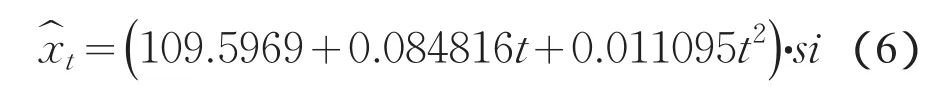
2.2 SARIMA模型的建立
2.2.1 数据分析(平稳化)
根据图3对应的季节因子,利用式(5)、式(6)计算2011年9月至2012年8月海南过夜旅游人数得到预测结果,见表2.
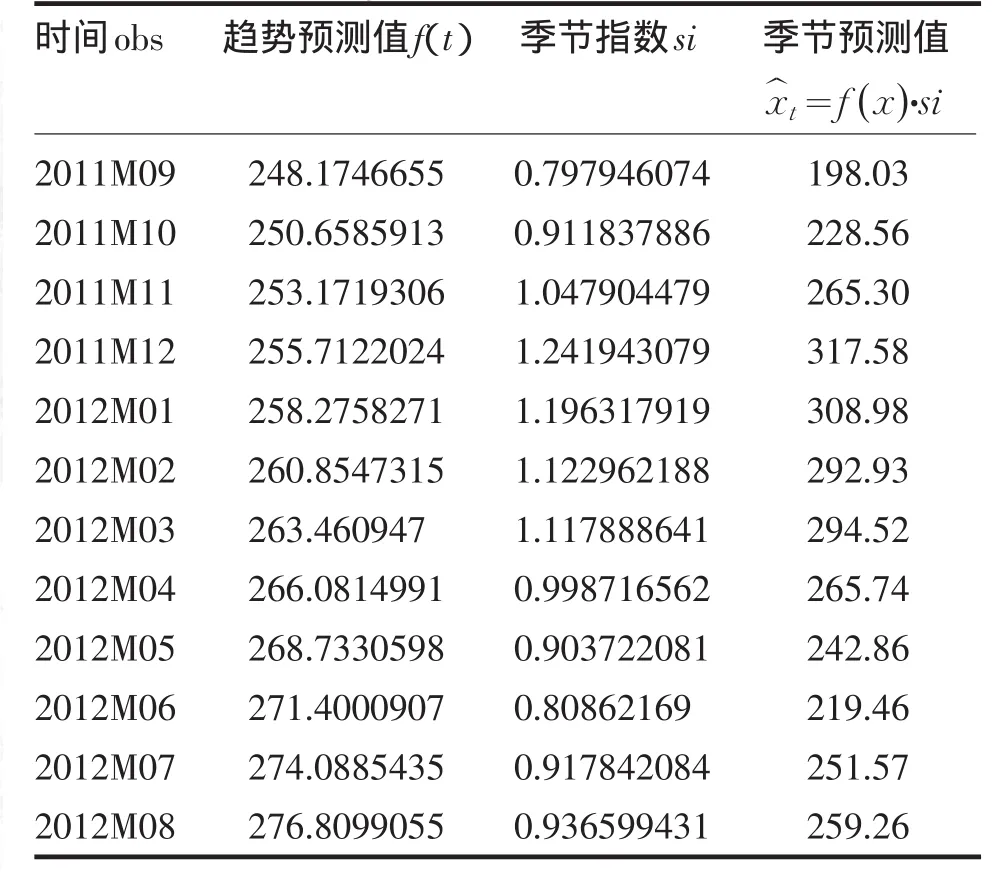
表2 2011年9月至2012年8月海南过夜旅游人数预测结果Tab.2 The forecast number of overnight tourist in Hainan from September 2011 to October 2012
利用Eviews6对2011年9月到2012年8月的数据作时序见图6,图6表明:序列随时间变化存在周期性与趋势性,从而该序列为非平稳的时间序列.由于数据具有指数函数增长趋势,为了减小数据的这种波动影响首先对其取对数后进行一阶差分,即yt=ln(xt)-ln(xt-1),再检验模型是否含有季节性.所得的自相关图中,当K=12时序列的自相关系数是0.684,大大超出了随机区间的范围,有显著的差异,表明该序列具有周期性的季节波动.要使数列平稳需再进行一次季节差分,即zt=yt-yt-12,所得自相关图,见表3.
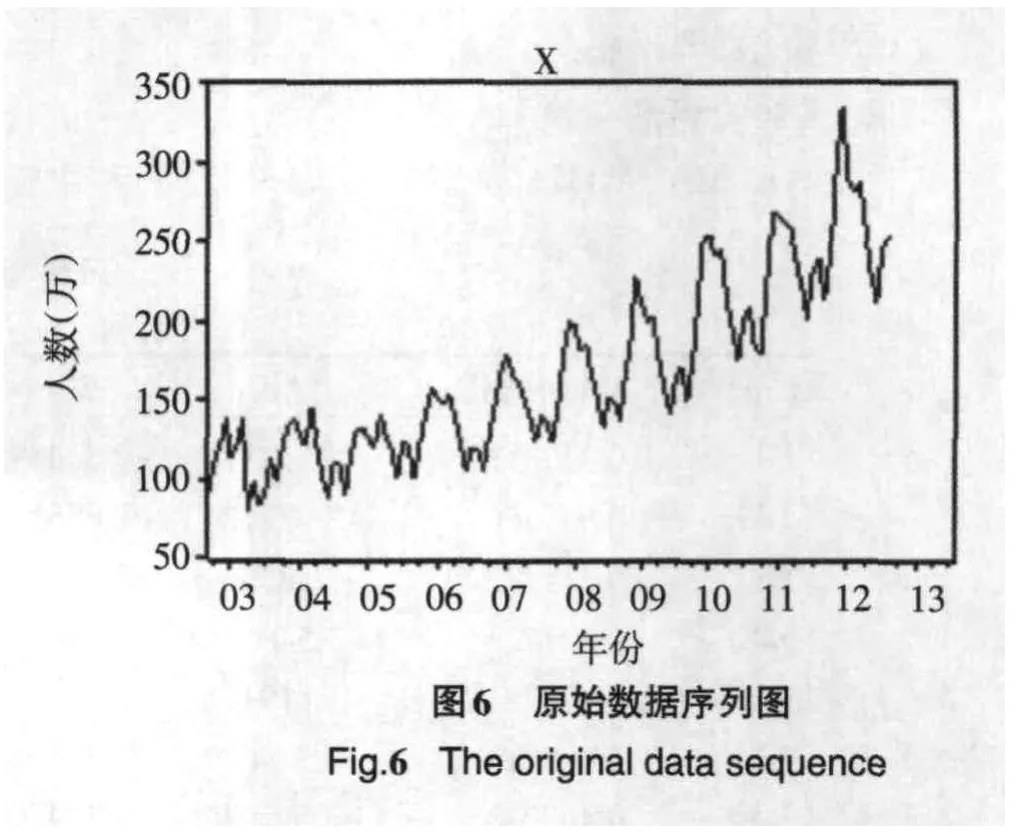

表3 一次差分与一次季节差分后的自相关表Tab.3 A difference and once the season differential autocorrelogram
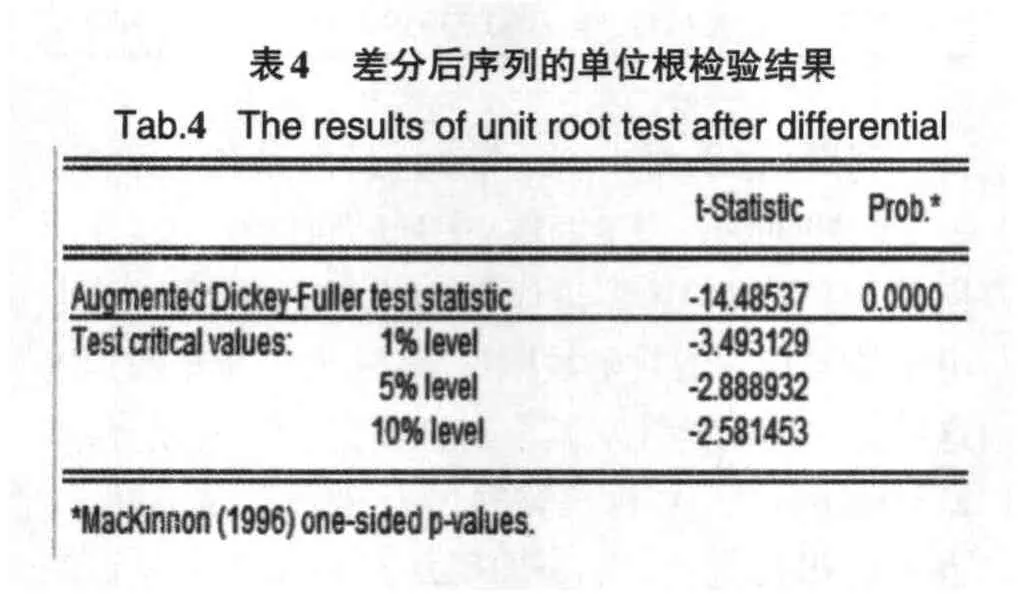
表3表明:当K>4时,序列的自相关系数很快的趋于0,即落入随机区间.对此时序进行单位根检验,所得结果见表4.
?
由表4知,t统计量的检测值为-14.48537小于所有置信区间的临界值,表明序列平稳.即:H0∶r=0H1∶r=1
t统计量的检验值<临界值,所以拒绝H0,序列没有单位根,即平稳.
2.2.2 模型的识别与检验
由AR、MA、ARMA模型的自相关与偏自相关特性,判定其模型类型参照表5.

表5 AR、MA、ARMA模型的自相关与偏自相关的识别与检验表[5]Tab.5 AR、MA、ARMA model's identification and inspection of ACF and PACF
由上述平稳化的过程可知:d=1,D=1;由于K=12时样本的自相关系数-0.084与偏自相关系数-0.202都不显著,为0,所以P=Q=1;再次由zt的相关图可以尝试建立(p,q)分别为(1,1),(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)的模型,然后进行取优,所得相关检验结果见表6.
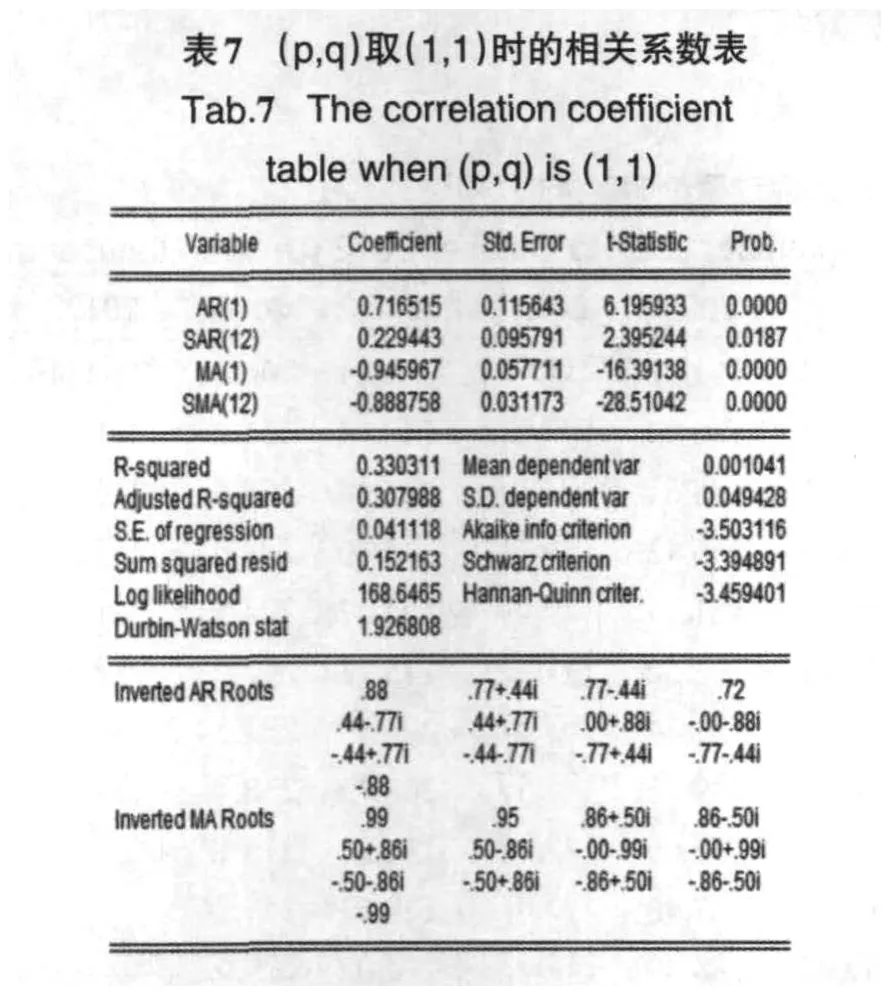
由表6知:首先,拟建立的七个模型都满足AR⁃MA过程的平稳条件(无单位根)及可逆条件(AR模型与MA模型可以相互转化),可知模型设定的合理.其次,残差序列的白噪声检验的相伴概率(p-Q)的值看出,各模型残差均是白噪声过程,满足独立性的假设.再次,根据模型的平均绝对百分误差(MAPE)的值都小于10,可知模型拟合的都很好.最后,鉴于AIC与SC准则与希尔不等系数(Theil Inequality coefficient)、样本决定系数(Ad⁃justed R2)及考虑到AR模型是线性方程估计,实际建模时一般希望用高阶的AR模型替换ARMA模型,因此选定(p,q)取(1,1)时进行建立SARIMA(1,1,1)×(1,1,1)12模型比较合适.拟合模型的相关系数见表7.
代入(1)式整理成方程,见式(7).
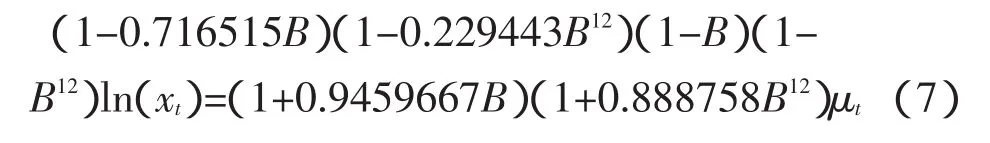
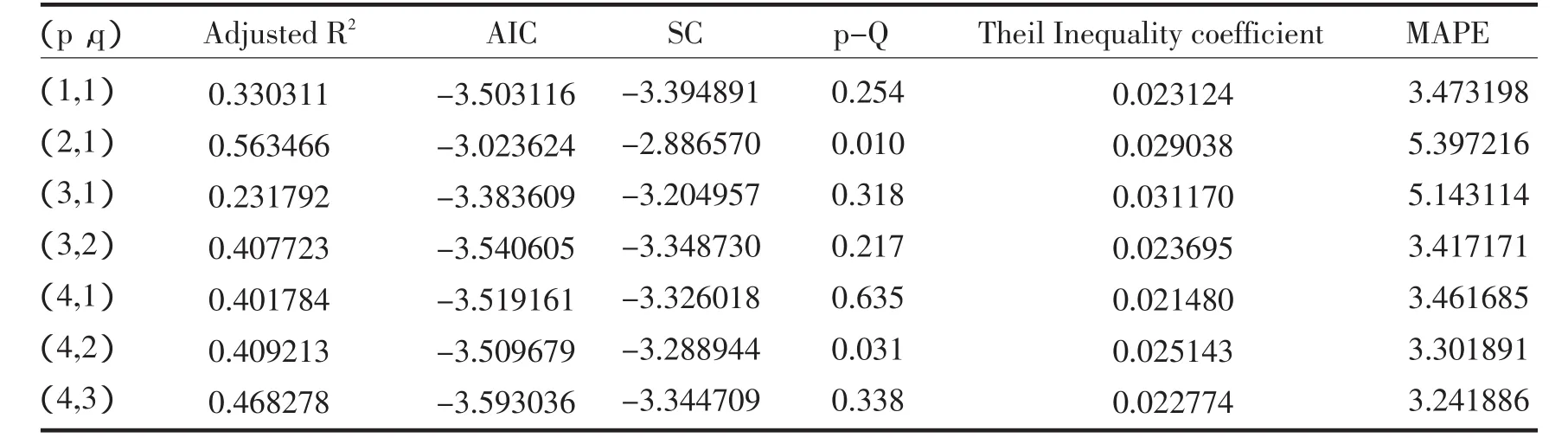
表6 模型检验结果Tab.6 The results of model
?
其中μt为上述检验为零均值的白噪声序列,即原序列的残差序列是白噪声序列.
2.2.3 预测
根据(7)式,直接在Eviews6中预测2011年9月至2012年8月的旅游人数,所得结果见表8.对海南2012年9月-2013年8月的旅游人数作出预测,所得结果见表9.
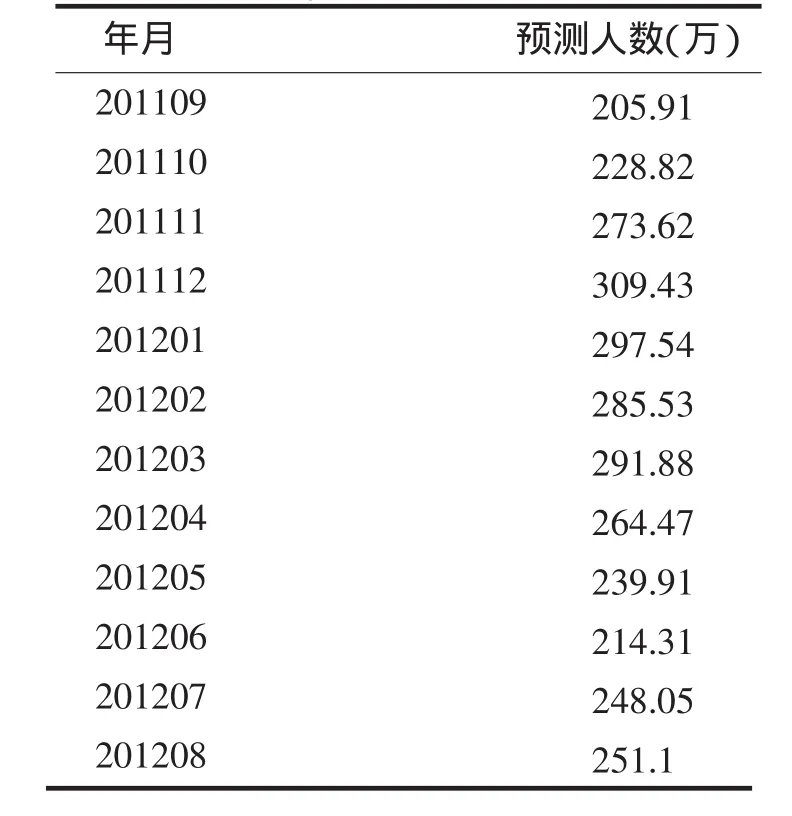
表8 2011年9月至2012年8月海南过夜旅游人数预测结果Tab.8 The forecast number of overnight tourist in Hainan from September 2011 to October 2012
2.3 两种模型预测结果比较
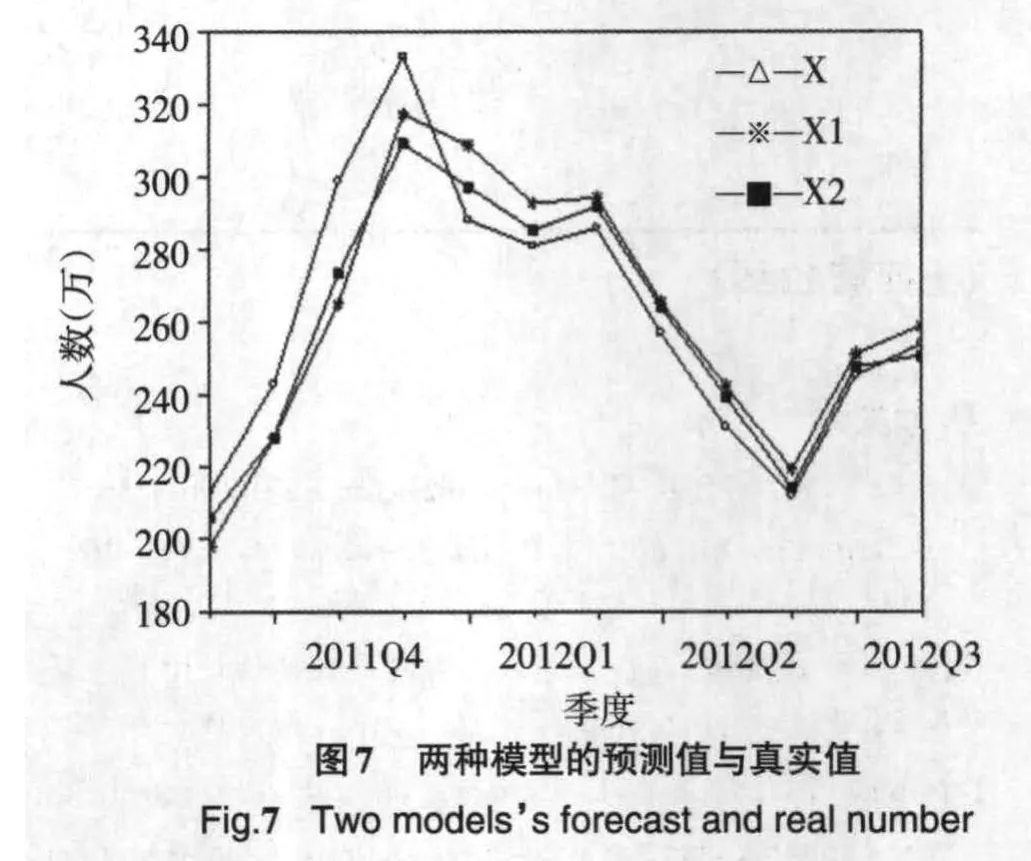
1)比较季节调整模型与SARIMA模型对2011年9月到2012年8月海南过夜旅游人数的真实值与预测值的均方误差发现:对于季节调整模型的均方误差为15.26,而SARIMA模型所得的均方误差为12.15,从而可知SARIMA模型预测较优.根据数据作季节调整模型与SARIMA模型拟合图,结果见图7.其中X表示实际值;X1表示季节调整模型的预测值;X2表示SARIMA模型的预测值.
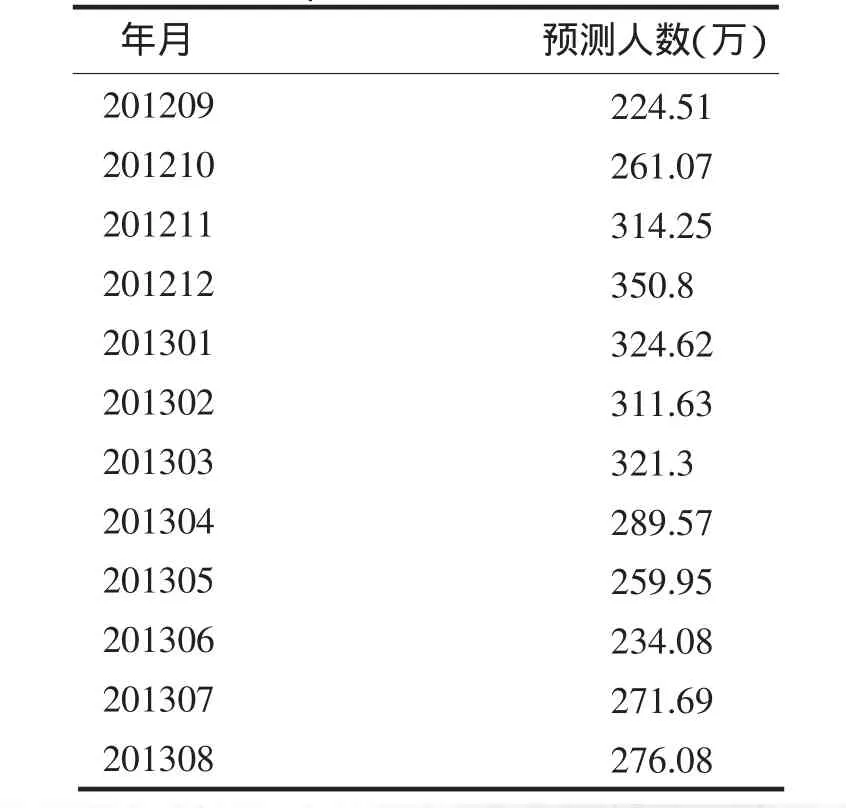
表9 2012年9月至2013年8月海南过夜旅游人数预测结果Tab.9 The forecast number of overnight tourist in Hainan from September 2012 to October 2013
[1] 易丹辉.数据分析与Eviews6应用[M].北京:中国人民大学出版社,2008:103-111,122-151.
[2] 王振龙.时间序列分析[M].北京:中国统计出版社,2000:184-192.
[3] 安潇潇.ARMA相关模型及其应用[D].河北:燕山大学硕士学位论文,2008.
[4] 张晓峒.计量经济学软件Eviews2使用指南[M].天津:南开大学出版社,2004:29-47.
[5]过晓芳.基于ARIMA模型的国内旅游人数预测研究[J].科技信息,2007(8):21-22.
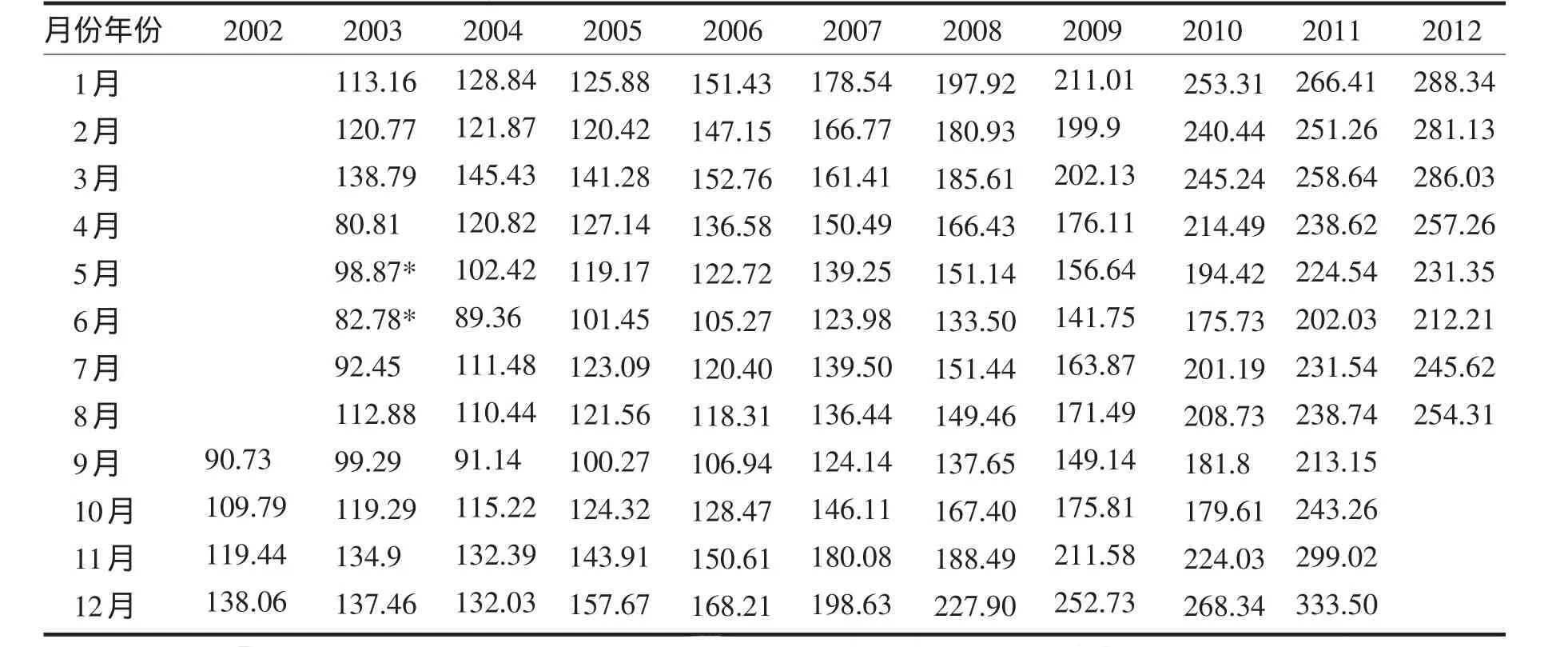
附表1海南省2002年9月至2012年8月接待过夜旅游者人数(单位:万人)Extra Tab.1 The number of overnight tourist in Hainan from September 2002 to October 2012(Unit:ten thousand)
