物性参数对纳米流体强化换热的影响
2013-03-22胡锐,李凌,杨茉
胡 锐, 李 凌, 杨 茉
(上海理工大学能源与动力工程学院,上海 200093)
沿流体流动方向增加扰动是一种有效的强化换热方法,比如波纹板通道、矩形槽通道、锯齿形通道等,通过改变通道形状改善流动状况,从而强化了换热.一直以来有大量的文献对各种不同形状通道内的对流换热进行了数值模拟[1-2].然而随着科技水平的进一步提高,目前仅从改善通道的几何形状来强化换热已经达到了一个极限,再进一步提高换热系数的效果已经不明显了.为了满足工业发展对强化换热的要求,新的研究目标是从工质本身入手研制具有高传热性能的高效新型换热工质.提高液体导热系数的一种有效方法是在液体中添加金属、非金属或聚合物固体粒子.早期,在液体中添加的粒子都局限于毫米或微米级,由于这些毫米或微米级粒子在实际应用中容易引起磨损、堵塞等不良结果,而大大限制了其在工业实际中的应用.纳米材料科学的迅速发展给强化传热领域带来了新的机遇,纳米流体就是以一定的方式和比例在液体中添加纳米级金属或非金属氧化物粒子而形成的一类新的传热冷却工质,相对于包含有微型尺寸的颗粒的流体而言,纳米流体更加稳定,并且不易堵塞流动通道,因而被认为是未来最理想的换热工质之一.实验发现相对于构成纳米流体的基础流体而言,纳米流体的导热性能得到了很大程度的提高[3-4].然而问题是纳米流体导热性能的显著提高却无法用现有的理论进行解释,因而大量的文献对此问题展开了实验和数值模拟研究,以期望对此现象能给出合理的解释[5-6].纳米流体相对于基础流体而言具有更好地导热性能,然而对流换热系数不仅与导热系数有关,还与其它物性参数有关,纳米流体的密度、比热、黏度、热扩散系数等物性参数相对于基础流体也会发生变化,从而对换热系数也有影响.本文考虑了纳米流体的热物性参数变化情况,通过对其在通道内的流动换热情况进行模拟研究,探讨了纳米流体在不同工况下的强化换热作用.
1 物理问题与数学描述
模拟研究了铜-氩纳米流体在通道内的流动和换热情况,所考虑通道模型为周期性矩形槽通道,计算区域为一个几何周期,如图1所示.
假定流动和换热为常物性二维层流并且已进入了周期性充分发展,其无量纲控制微分方程组为


式中,U,V分别为坐标x方向和y方向无量纲速度分量;F为无量纲时间变量;P为无量纲压力;θ为过余温度,θ=T-TW(TW为壁温);Pr为Prandtl数;Re为Reynold数.在对方程进行无量纲化时取流通截面高度的2倍作为整个问题的参考尺度;取最小流通截面处的平均流速(最大截面平均流速)作为无量纲流速的参考速度.

图1 计算通道示意图Fig.1 Computation domain of the channel
忽略了流动主流方向的导热.计算区域的无量纲长度为2.0,高度为0.5,满足的边界条件为

式中,SP为一个周期的无量纲长度;Θ为无量纲过余温度,定义为

式中,Tb为截面平均温度.计算时采用了扩大区域法来实现周期性边界条件,并采用了整体解法处理固体的矩形突出部分,并附加了以下条件:

本文采用SIMPLE算法,QUICK格式,计算的初始条件为U=0,V=0,θ=1.
2 计算结果及分析
2.1 纳米流体物性参数的计算
以平行板通道为例对算法进行了检验,并对时间步长和网格数进行了验证.纳米流体相对于基础流体,主要改变的是密度、导热系数、黏度以及热扩散系数等物性参数,为了研究纳米流体对流动换热的强化作用,分别模拟了液氩以及体积分数φ分别为1.0%,1.5%,2.0%的铜-氩纳米流体在周期性矩形槽通道内的对流换热情况.
在确定液氩和铜-氩纳米流体的物性参数时,计算式为

式中,ν为运动黏度,m2/s;a为热扩散系数,m2/s,且

式中,μ为动力黏度,Pa·S;λ为导热系数,W/(m·K).对于纯液氩,以及体积分数分别为1.0%、1.5%和2.0%的纳米流体,在文献[7]中应用分子动力学方法计算了其导热系数分别为0.126,0.144,0.150和0.152W/(m·K).纳米流体的密度和比热的确定分别按照不同体积分数混合和不同质量分数混合的方法来计算.在86K时,液氩的密度为1 401kg/m3,比热为984J/(kg·K),铜的密度为8 960kg/m3,比热为390J/(kg·K).在计算纳米流体密度时,得不同体积分数的纳米流体的物性参数如表1所示.

表1 纳米流体的物性参数Tab.1 Physical parametersofnanofluids
2.2 不同体积分数比纳米流体在通道内的流动换热
对不同Re下液氩以及不同体积分数的纳米流体的流动和换热情况进行了模拟,得到了流场和温度场的分布.图2和图3分别为Re=1 000时液氩和体积分数为2.0%的纳米流体在不同时刻(从上至下依次为无量纲时间等于1 500,1 600,1 700)下的流场和温度场分布.
从图2和图3中可以看出,基础流体和纳米流体的流场变化不大,但是温度场的分布有所不同,并且都随时间发生变化,这是因为相对于基础流体而言,纳米流体的导热系数得到了很大的提高.
2.3 纳米流体的强化换热
对Re分别为200,400,600,800及1 000这5种情况下的对流换热情况进行了模拟计算,结果发现纳米流体的摩擦阻力系数相对于基础流体没有明显变化,但是换热系数却有不同程度的提高.为了说明纳米流体相对于基础流体对换热的强化作用,定义了相对换热系数
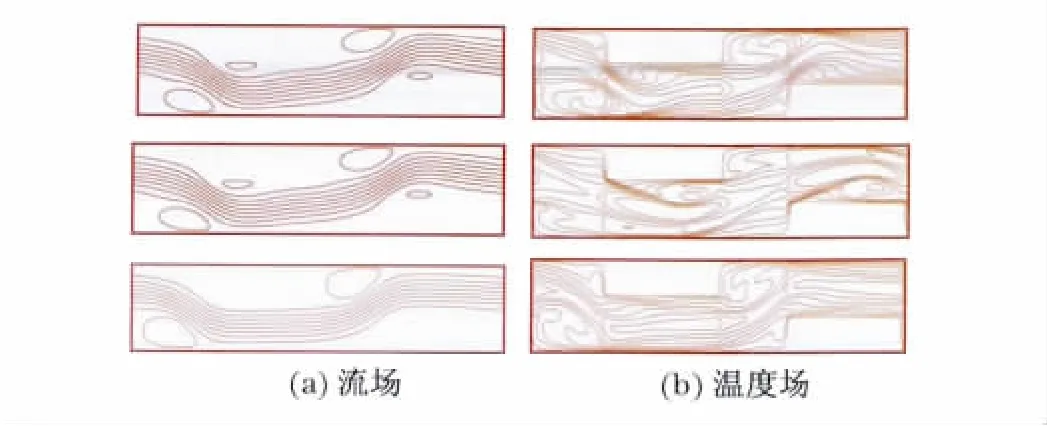
图2 液氩在不同时刻的流场和温度场Fig.2 Flow field and temperature field of Ar at different times
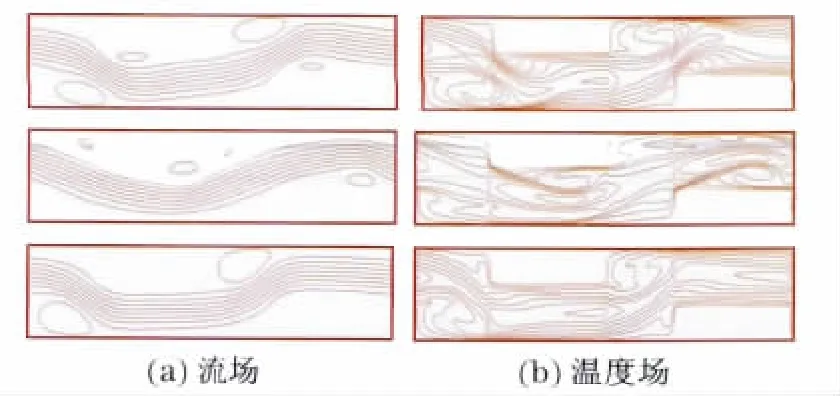
图3 纳米流体在不同时刻的流场和温度场Fig.3 Flow field and temperature field of nanofluids factor percent at different times

式中,hn,hAr分别为纳米流体和基础流体液氩的换热系数,W/(m2·K).
图4为Re=200时不同体积分数的纳米流体的相对换热系数.由图4可以看到相对于基础流体,纳米流体的换热系数都有很大程度的提高,并且纳米颗粒的体积分数越大纳米流体的强化换热作用越显著.实际上,由于不同体积分数的纳米流体的黏度不相同,所以当Re相等时,其速度也不一样,当流体的流动速度越大时,换热系数是越大的.因此可知当不同体积分数的纳米流体的流速相同时,体积分数越大的纳米流体的换热系数必定也越大.

图4 不同体积分数的纳米流体的换热系数Fig.4 Heat transfer coefficient of nanofluids with different volume fractions
纳米流体的强化换热作用与纳米流体的纳米颗粒所占的体积分数、纳米颗粒的直径、纳米颗粒的形状等因素都有很大的关系.本文在研究的过程中采用了球形的纳米颗粒,并且只考虑了一个纳米颗粒的存在,即纳米颗粒的体积分数越大相应的纳米颗粒的直径就越大.文献[7]表明纳米颗粒的直径越大,在纳米颗粒表面形成的液体薄层的厚度就越大.由于液体薄层内分子的规则排列使得薄层的导热性能比基础流体要高,因而其对整个纳米流体导热物性的贡献就越大,使得整个纳米流体的导热物性显著提高.
进一步研究了当纳米流体的物性参数一定时,流速对换热系数提高程度的影响.图5为3种不同体积分数的纳米流体在不同Re下的相对换热系数.

图5 不同体积分数的纳米流体在不同Re下的换热系数Fig.5 Heat transfer coefficient of nanofluids with different volume fractions under different Re
由图中可以看到纳米流体的换热系数的增大与Re有关.当体积分数一定时,当Re较小即流速较低的时候,纳米流体换热系数的提高比较显著,而随着Re的逐渐增大,换热系数的提高程度逐渐减小.说明当流体的物性参数一定时,Re越大即纳米流体的流速越大时,纳米流体的强化换热效果越不明显.笔者认为这是因为当Re较小的时候,流体的流速较小,壁面与流体之间的总换热能力与流体内部能量的传递速度有关,即主要的热阻在流体的内部,因而流体的导热性能越好总的换热系数就越强.而当Re较大的时候,流体的流速很大,此时壁面与流体之间的换热能力的提高主要在于能量从壁面传递给流体的这一个过程,即主要的热阻在于流体和壁面之间,因而壁面处能量的传递速度很大程度上决定了整个通道的总换热系数.因为纳米流体的强化换热作用主要体现在流体的导热性能的提高,所以Re越大所导致换热能力增强的效果反倒不如Re小的时候显著.
3 结 论
a.由于导热性能相对于基础流体有了提高,纳米流体有效地增加了换热系数.当流速一定时纳米流体的体积分数越大,纳米流体的导热系数越大,从而相应的换热系数也越大.
b.对于相同体积分数的纳米流体,换热系数提高的程度与流体的流速有关.当流速较小的时候,纳米流体换热系数相对于基础流体而言提高的程度比较大,而随着流速的增大纳米流体换热系数提高的程度逐渐下降.
[1] Dejong N,Jacobi A.Flow,heat transfer,and pressure drop in the near-wall region of louvered-fin arrays[J].Experimental Thermal and Fluid Science,2003,27(3):237-250.
[2] Yucel N,Dinler N.Numerical study of laminar and turbulent flow through a pipe with fins attached[J].Numerical Heat Transfer:Part A——Applications,2006,49(2):195-214.
[3] Herman C,Kang E.Comparative evaluation of three heat transfer enhancement strategies in a grooved channel[J].Heat and Mass Transfer,2001,37(6):563-575.
[4] Xie H,Wang J,Xi T,et al.Thermal conductivity enhancement of suspensions containing alumina particles[J].J Appl Phys,2002,91(7):4568-4572.
[5] Yang Y,Zhang Z,Grulke E.Heat transfer properties of nanoparticle-in-fluid dispersions(nanofluids)in laminar flow[J].International Journal of Heat and Mass Transfer,2005,48(6):1107-1116.
[6] Das S,Choi S,Patel H.Heat transfer in nanofluids-a review[J].Heat Transfer Engineering,2006,27(10):3-9.
[7] Li L,Zhang Y,Ma H,et al.Molecular dynamics simulation of effect of liquid layering around the nanoparticle on the enhanced thermal conductivity of nanofluids[J].J Nanopart Res,2010,12(3):811-821.
