铣削加工曲面残余应力有限元分析

曾红，韩笑，陈燕燕，王延忠，吴林峰

(1.辽宁工业大学机械工程及自动化学院，辽宁锦州121001;2.北京航空航天大学机械制造及自动化学院，北京100191)

残余应力是消除外力或不均匀温度场等的作用仍留在物体内的自相平衡内应力。残余应力对于构件的疲劳强度、应力腐蚀、形状精度等均有重大的影响，而它的形成又随构件的材质、形状、成形与加工工艺过程等的不同而异。如何评定残余应力的大小、调整残余应力的分布、减小或消除残余应力对工程的影响已成为人们广泛关注的问题[1]。因此，分析加工过程中加工参数对残余应力的影响，对于优化切削过程和防止加工零件过早疲劳破坏，是很有必要的。

目前的仿真分析多为采用有限元仿真方法对平面进行的二维切削仿真和简单的平面三维仿真，通过对切削过程的模拟，研究切削用量、刀具参数对已加工表面残余应力的影响规律。而目前尚无针对曲面的铣削加工过程的低应力加工仿真，因此有必要开展曲面的低应力切削控制研究。

1 残余应力的产生机理

已加工表面残余应力产生的原因，可以概括为机械应力和热应力引起的塑性变形效应[2]。

(1)机械应力塑性变形效应

如图1所示，在剪切区，金属切削层在切削速度方向上承受压应力，使已加工表面在该方向产生残余拉应力。在刀/工区，切削层金属沿着刀刃钝圆面流动时受到刀具的挤压而产生塑性流动，使表层发生了延展现象。而里层金属发生弹性变形，对表层的延展起到牵制作用。之后，切削层金属受到后刀面强烈的摩擦作用，使表层发生大塑性变形，而里层金属发生弹性变形。切削过后，刀具的作用力消失，里层金属的弹性变形趋向恢复，但受到表层金属的牵制，因而在里层产生拉应力、表层产生压应力。

图1 切削变形区

(2)热应力塑性变形效应

在剪切区，由于强烈的塑性变形，产生变形热;在刀/工区，金属受到钝圆面和后刀面的挤压、摩擦，产生塑性变形热和摩擦热。这些热使得工件表层的温度比里层的高，表层的膨胀速度比里层大，但同时又受到里层的阻碍，使表层产生压应力。当切削过后，表层和里层的温度都下降到室温，表层收缩多，里层收缩少，表层的收缩受里层的牵制，因而使表层产生拉应力、里层产生压应力。

在切削过程中，引起不均匀塑性变形的机械应力和热应力是同时存在的，所以残余应力的计算是一个热－力耦合热弹塑性问题。

2 有限元模型的建立

进行曲面的铣削加工仿真过程时，材料的设定基于如下假设进行:

(1)工件材料为理想热－弹塑性体，均匀连续、各向同性、不可压缩;屈服极限服从Mises 准则，切屑的塑性流动过程连续且稳定。

(2)刀具和工件、切屑之间的摩擦因数恒定，不随温度、材料物理性能变化而变化。

(3)刀具为刚体，不随切削过程发生变形。

由于塑性变形和传热发生在同一空间域和时间域，而二者又分属不同的物理问题，分析时基于不同的基本理论[3]。为此，要采用热－力耦合的有限元算法。为在仿真过程中模拟以上热、应力－应变耦合的工件变形和应力应变状态，需要能描述材料在大应变、宽应变率范围以及宽温度范围内力学行为的本构模型。文中采用的Johnson-Cook模型是描述金属材料相关动态响应的本构模型，适用于描述金属材料从低应变率到高应变率下的动态行为，考虑了温度、应变率和应变等因素。

文中的拟加工椭球面两个方向的主曲率分别为K1=0.005 77，K2=0.013 82，即椭球面的长短轴分别为R1=173 mm，R2=72 mm。工件材料为常用的45号钢，该材料的Johnson-Cook参数[4]如表1，失效参数如表2。刀具采用的为φ8 mm的球头铣刀。其中，图2为Abaqus 中的分析模型。切削过程中工件外侧定义为全约束，刀具绕刀轴旋转的同时，刀尖沿着工件表面做曲线运动。

表1 Johnson-Cook参数

表2 失效参数

图2 Abaqus 中的模型

3 表面残余应力的结果分析

文中采用主轴转速分别为3 000、5 000、8 000 r/min，单齿进给量分别为0.05、0.1、0.2 mm/齿，切削深度分别为1、2、3 mm 作为曲面铣削加工的参数，对加工过程进行了仿真分析，得到了残余应力在不同的参数条件下的变化曲线，见图3。

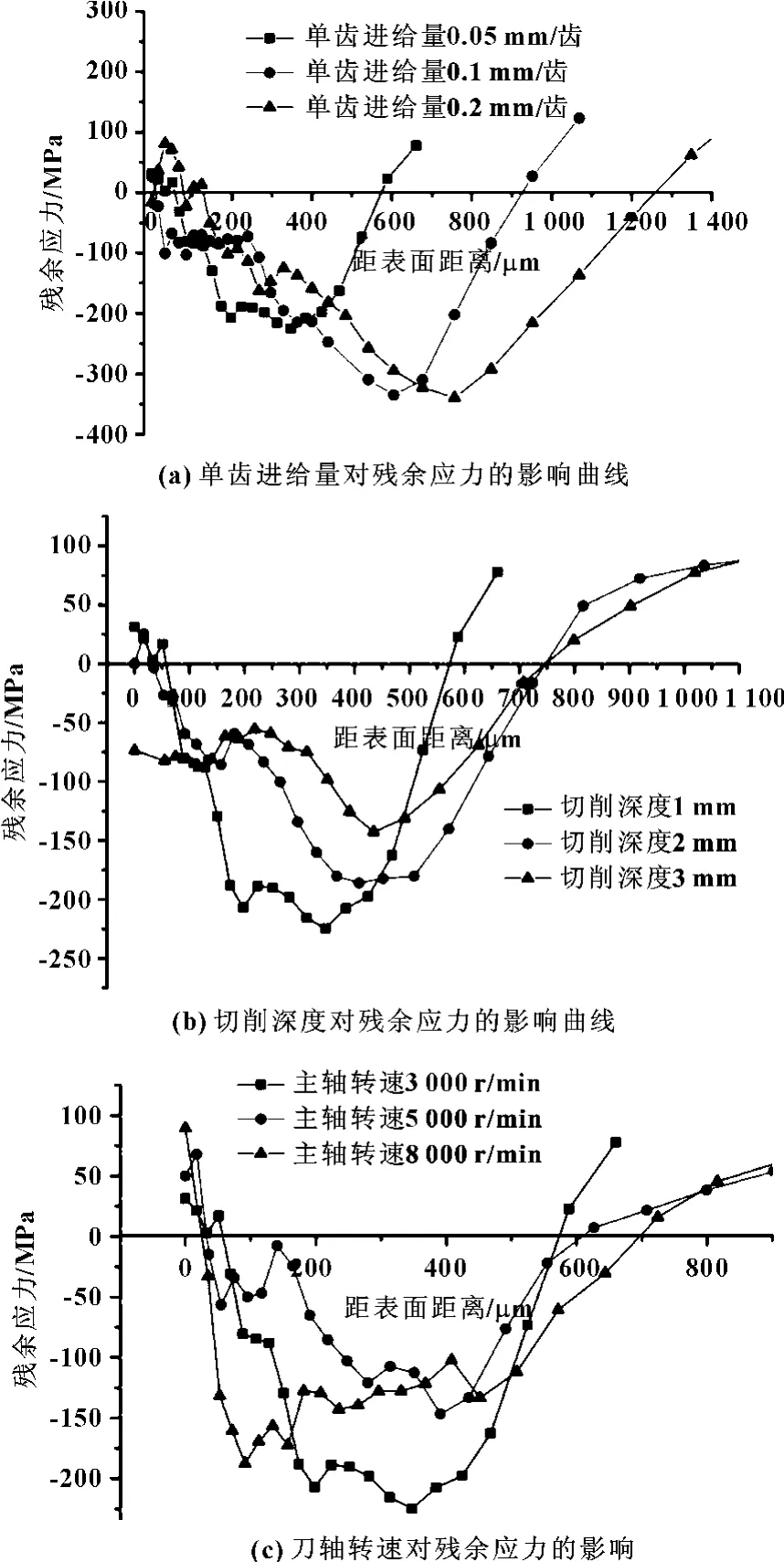
图3 表面残余应力变化曲线

图3为单齿进给量、切削深度、主轴转速不同的情况下，表面残余应力的变化曲线。可以看出:距离表面一定深度区域的残余应力大部分位于0 线以下，是表面的残余压应力，压应力呈先增大后减小的变化趋势。其中，图3(a)是在主轴转速为3 000 r/min、切削深度为1 mm时，不同的单齿进给量下残余应力的曲线图。可以看出:随着单齿进给量的增大，表面残余拉应力增大，出现最大残余压应力的深度由0.35 mm 增大到0.8 mm，由压应力转换为拉应力的深度即塑性变形深度由0.58 mm 增大到1.25 mm;图3(b)是主轴转速为3 000 r/min、单齿进给量为0.05 mm/齿时，在不同的切削深度下残余应力的曲线图。可以看出:随着切削深度的增大，工件残余压应力的深度也随之增大，工件发生塑性变形的深度加深。产生残余压应力增大这一现象的原因是:由于切削深度增大，增大了切削过程中的切削力，刀具对工件的作用力增大，导致工件残余压应力的范围加深。

图3(c)是单齿进给量为0.05 mm/齿，切削深度为1 mm时，不同的主轴转速下残余应力的曲线图。可以看出:随着刀轴转速的提高，表面残余压应力有所减小，拉应力增大;同时，塑性变形深度也随之增大。产生这一现象的原因是:在相同的进给速度下，主轴转速增大了，增大了刀具与工件之间的摩擦热量，使工件表面的残余拉应力增大，压应力减小。

4 基于有限元的正交试验

通过以上曲线图的分析，只能得到在某一参数变量条件下，残余应力的变化趋势，不能比较不同的切削参数对残余应力的影响程度。为了得出主轴转速、单齿进给量及切削深度等切削参数对残余应力影响程度，基于有限元分析模型，设计了一组四因素三水平的正交试验。表3所示为L9(34)四因素三水平正交试验的因素及水平值。文中只选择了3个元素，即主轴转速、切削速度(铣削模拟中为单齿切削量)、切削深度[5]。

表3 因素及水平值

表4为曲面切削加工模拟结果正交表。利用有限元软件进行了9次切削仿真，得到己加工表面残余应力的结果，包括切削速度方向的残余压应力平均值、最大压应力值及塑性变形深度。

表4 切削模拟结果正交表

从表4的极差值R分析中，可以看出:主轴转速取3 000 r/min时，表面的残余压应力最大，塑性变形深度最小;单齿进给量为0.2 mm/齿时，表面压应力最大，塑性变形深度最大;切削深度为3 mm时，表面残余压应力比其他两水平大，塑性变形深度也大。同时还可以看出:三因素中，单齿进给量对工件塑性变形深度影响最大，切削深度次之;切削深度对表面残余压应力的影响最大，单齿进给量次之;主轴转速对两者的影响都最小。在实际加工过程中，由于切削深度的增大会导致加工精度的降低，因此，为增大表面残余压应力与压应力在深度上的分布范围，应在满足加工精度要求的切削深度前提下，尽量增大加工过程中的单齿进给量。

5 结束语

通过对曲面铣削加工过程的三维仿真，研究了曲面铣削加工过程中残余应力的产生机制和影响因素，利用三维有限元仿真验证了切削过程中工件、切削应力变形的切削理论;并通过针对不同主轴转速、单齿进给量和切削深度组合的仿真实例，得到了切削表面的残余应力在进给方向上沿深度的分布，得到了不同主轴转速、单齿进给量和切削深度的残余应力变化曲线，并进行了分析。

仍有需要进一步探讨的地方，如:

(1)计算过程中刀具和工件、切屑之间的摩擦因数是随温度等变化而变化的，在文中的分析中没有涉及，需要进一步研究。

(2)实际加工过程中，刀具并非完全的刚体，存在一定的损耗，而文中在计算过程中，将刀具假定为刚体，未考虑刀具的磨损情况，需作进一步的研究。

(3)目前的仿真参数仅考虑了加工参数，并未考虑工件及刀具的材料及刀具的几何外形，后续还可进一步对更多的参数进行仿真分析。

【1】刘建明，朱小清.汽车渗碳淬火齿轮的表面残余应力研究[J].热处理，2006(2):50－51.

【2】蔡在宣.金属切削原理[M].上海:同济大学出版社，1994.

【3】张铁茂.金属切削学[M].北京:兵器工业出版社，1991.

【4】陈刚，陈忠富，徐伟芳，等.45 钢的J-C 损伤失效参量研究[J].爆炸与冲击，2007，27(2)，131－135.

【5】袁哲俊.金属切削实验技术[M].北京:机械工业出版社，1988.

【6】郭培燕.高速切削加工表面残余应力的分析和模拟[D].青岛:山东科技大学，2007:17－22，42－48.

【7】JOHNSON K L.Contact Mechanics[M].Cambridge University Press，1985.

【8】周军.铝合金7050－T7451 直角切削表面的残余应力研究[J].工具技术，2010，44(2):12－16.

【9】何庆稀.铝合金7475 已加工表面残余应力的数值模拟[J].制造，2008，46(6):46－49.