定点DSP中高精度小数乘法运算研究
2013-03-19周泽湘欧阳明星
周泽湘,欧阳明星
(广东松山职业技术学院,广东韶关512126)
0 引言
DSP(Digital Signer Processor)是一种用于数字信号处理运算的专用处理器,内部采用了改进型哈佛结构和多总线的并行结构,以及一些专用的硬件处理单元,使得DSP 数字信号处理器能在单周期内完成复杂的数字信号处理的数学运算。DSP 内部还集成有专用并行硬件单元,其结合汇编语言编程实现数字信号处理的核心算法可以提高程序效率[1]。DSP所处理的数据类型有定点DSP 和浮点DSP,其中以定点DSP 在市场上较为常见,而如何在定点DSP 中实现小数运算是一个关键问题。本文论述了在定点DSP 中实现小数乘法运算的方法,研究了不同Qm.n 规格数精度问题,并详细讨论和分析了在定点DSP 中进行小数运算的操作方法。
1 定点数的Qm.n 表示方法
1.1 Qm.n 格式
字长是计算机CPU 在一次操作中能处理单位字的长度。字长决定了数的范围和精度,根据DSP 型号不同,有16、24 及32 位等不同字长。定点DSP 处理的都是定点数,以一个16 位字长DSP 为例,规定最高位为符号位S,S 为0 表示正数,S 为1 表示负数,余下15 位按其二进制权值以补码形式表示数的大小。当表示小数时,先确定小数点在16 位数中的位置即定标,小数点右边的二进制权值为负,小数点左边的二进制权值为正。正权值表示数的整数部分,负权值表示数的小数部分,这样人为地扩大了数的表示范围,使得在定点DSP 中可以表示小数。这种在定点DSP 中表示小数的方法称为Qm.n 表示方法,其中m 表示整数二进制位数,n 表示小数二进制位数,Qm.n 又可用Qn 来表示,如Q0.15 在实际中通常使用Q15 表示。在定点DSP 中,相同字长的CPU 不同Qm.n 格式表示数的精度和范围均不同,Qm.n 的数的表示方法如图1所示[2]。以Q3.12 为例,即在16 位数中,除1位表示数的符号外,用3 位二进制表示整数,用12 位二进制表示小数,m 决定数的范围,n决定数的精度,二者互斥,显然m 越大表示数的范围越大,但表示数的精度越低;n 越大表示数的范围越小,但表示数的精度越高,故Q3.12 表示数的范围为-8~8,表示数的精度为1/212,即Q 值越大,表示数的精度越高。
比如执教贾平凹的《月迹》时,首先让学生充分感知课文,反复练读达到“文通字顺”;然后让学生选择自己喜欢的描写月光的句子,读一读,并引导学生交流喜欢的原因,从而帮助学生再现画面,体会意境;最后让学生配上柔柔的乐曲,图文结合,美美地赏读,在赏读中进一步感悟语言,形成语感,在美读中那皎洁的月光也仿佛洒向了孩子那稚嫩的心灵。
我走进家门时,刘铁头已经等我好一阵了。儿子正往煤球炉上坐锅添水准备熬汤。刘铁头看着儿子忙活了一阵,对我竖了竖大拇指。穷人的孩子早当家啊,你看才多大个孩子就中用了,说到底,还是你有福啊四眼儿张。说着,就从塑料袋里掏出把炒花生米往儿子兜里放。

图1 Qm.n 的数的表示方法
不同字长的CPU,Q 值越大,表示数的精度越高,能分辨的小数越小,常见的Qm.n 格式数的范围和精度如表1所示。
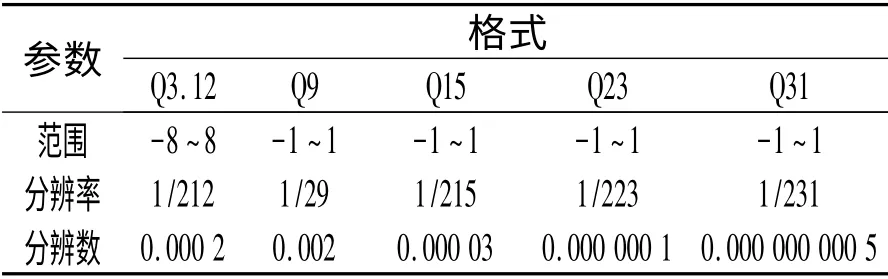
表1 常见的Qm.n 格式数的范围和精度
1.2 Qm.n 数的规格化与反规格化
TI 公司生产的定点DSP 有C2000、C5000和C6000 等多种型号,C2000 系列DSP 主要用于控制领域;C5000系列DSP主要用于数字语音等领域;C6000 系列DSP 主要用于高端图像处理等[4]。TMS320F2812 是C2000 系列中的代表型号,字长为32 bit,TMS320C5402 为C5000 系列的典型型号,字长为16 bit,TMS3206402 为C6000 系列的典型型号,字长为32 bit。在定点DSP 中进行数字信号处理的小数乘法运算时,有几个关键问题值得研究:①参与运算的小数应表示成与DSP 的CPU 字长相适应的Qm.n 格式,如在TMS320C54x DSP 中输入数据使用Q15 格式规格化,而在TMS320F2812 DSP 中则需使用Q31 规格化。②在编译器中不能直接表示小数,以CCS2.0 编译器为例,在进行汇编语言编程时,在定点DSP 中无法编辑小数,在对小数进行规格化处理时,应写成定点数的形式,如0.3 按Q15 进行规格化,可以写成3* 32 768/10,其结果与0.3* 32 768 等价,这样避免了编译器出现小数,但需注意应先乘再除,否则无效。③在进行小数乘法运算时会产生冗余符号位,如0.5×(-0.375),按Q3 进行规格化处理,正确结果为1110100(-0.187 5=-12/26),当将其送入累加器时,为了保持乘积符号扩展为8 位结果11110100(-0.093 75=-12/27),扩展了一个多余的符号位之后导致结果错误,必须消除该冗余的符号位。DSP 乘法器有冗余符号位自动消除功能,在进行小数乘法运算时,将FRCT 位置为1后会自动将结果左移1 位,以确保结果正确。本例中11110100 左移1 位后结果为11101000(-24/27=-0.187 5)。④应避免乘法溢出,在DSP中,乘、加运算结果一般放在累加器中,累加器字长是CPU 字长的数倍,如TMS320C54x 的累加器字长为40 位,以保证多个16 位数运算时不会溢出。

表2 Q12 格式规格化与反规格化的数对比

表3 Q15 格式规格化与反规格化的数对比
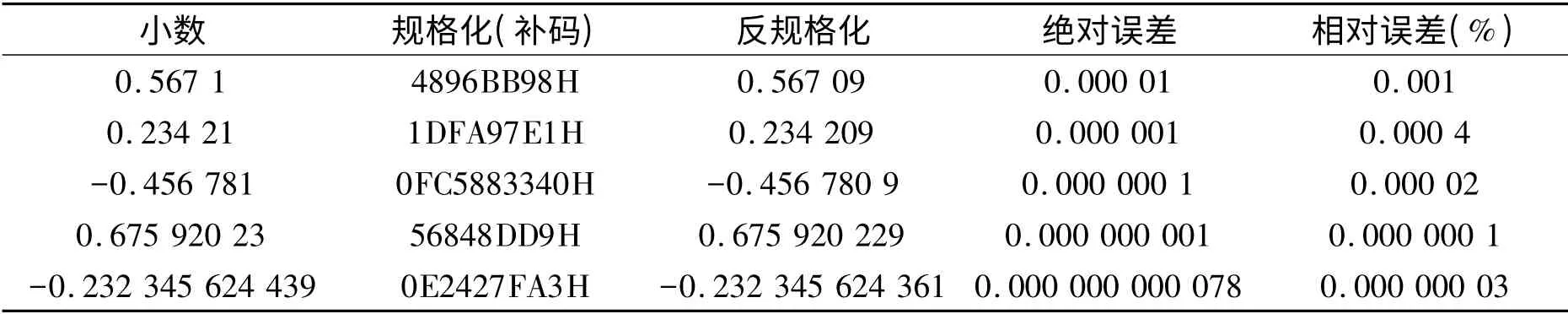
表4 Q31 格式规格化与反规格化的数对比
在TMS320C54x 定点DSP 中,进行小数乘法运算之前,先将ST1 寄存器中的FRCT 位置1,每次进行乘法运算之后DSP 自动将结果左移1 位,消除冗余符号位。在数字信号处理中,乘-累加运算是最常见的运算,如实现IIR和FIR 数字滤波,或FFT 快速傅里叶变换[5]。在DSP 中计算乘-累加运算如下式[4]:
由GC- MS分析得到的质谱数于NIST08.LIB和NIST14.LIB标准谱库的检索,查对相关质谱资料,分别对各峰加以确认,鉴定样品中的挥发性香气成分,用峰面积归一法分析各组成分相对含量。
2 DSP 中小数乘法关键问题
Qm.n 表示数的方法是人为设定的为了在定点DSP 中拓宽数的表示范围的一种表示方法,这种方法已被TI 公司所接受,并成为其定点DSP的LIB 库接口标准数据类型[2]。以TMS329C54x的定点DSP 为例,TI 公司提供的各种适用于定点DSP 使用的lib 库,进行小数运算时,输入、输出数据均采用Q15 格式[2-3]。DSP 无法自动识别这种数,在DSP 进行数学运算之前,应先将数按约定的格式进行规格化处理才能进行运算。DSP运算完成的结果依旧是一个定点数,需要将其按相反的规则进行反规格化处理。使用Qm.n 表示数时,规格化数的方法为将该小数乘以2n 并取整,反规格化时将运算得到的整数结果除以2n 还原成小数。若小数是负数,则应将结果进行补码操作。以小数0.768 93 为例,按Q15 规格化乘以32 768 得到结果为626CH,将626CH除以32 768 之后得到的结果为0.768 920。显然,数规格化之后与规格化之前有误差,这是由定点DSP 运算过程的四舍五入所造成。而这个误差与Qm.n 数精度有关,取0.567 1、0.234 21、-0.456 781、0.679 202 3、-0.232 345 624 439这5 个数,分别使用Q12、Q15、Q31 进行规格化和反规格化处理,其结果如表2~4所示。
“哦,我半个月前去外地出差,在那边遇到一个自称老贾的人,他卖给我的。看来我遇到的老贾八成就是你说的那个人了。”中年人说着抱紧了箱子,生怕孟导急了来抢。
3 小数乘法在DSP 中实现
由表2~4 可知,相同的数,使用不同的Qm.n 格式进行规格化处理,其误差相差50~200×104倍,当然,小数有效位数也影响规格化和反规格化结果。

其中,x = {0.35,-0.23,-0.4,0.1},a={0.6,0.5,-0.1,-0.2},输入数据为小数,计算结果y 也是小数。完成公式(1)中小数运算的步骤为:①建立.bbs 段,为x、a 分别保留4 个存储单元,为y 分配2 个存储单元,建立.data 段,存放8 个Q15 规格化的小数;②将.data 段数据搬移到.bss,分别赋值给x、a;③置位FRCT,以消除冗余符号位;④执行4 次MAC 指令,完成计算ai×xi运算;⑤保存结果到y。按该思路编程如下:

链接器的CMD 配置文件如下

在CCS2.0 中编辑编译程序并执行,RAM执行结果如图2所示。

图2 执行结果
进一步分析上述程序,每一步乘-累加运算结果分解如表5所示,将程序中MAC 指令改成MPY 单乘法指令,并分别将FRCT 置0 和置1 之后执行程序结果如表5 第4、第5 行所示。与原数相对照,第4 行受冗余符号位影响,所有结果均不正确,第5 行为FRCT 位置1后每次进行乘法运算后结果自动左移1 位,消除冗余符号位,与原数对照,结果正确,第7 行为MAC 运算结果。程序最后只将累加器高阶AH 保存于y 中,AL 值直接舍去,这是由于在TMS320C54x DSP 中,2 个16 位整数相乘,乘积总是“向左增长”,这意味着多次相乘后乘积将会很快超出器件数据位宽甚至溢出。要将32 位乘积保存在数据存储器中,需要开销2 个机器周期以及2 个字的存储单元,此外由于乘法器为16 位,后续的递推运算无法输入32 位乘积数,而小数乘积总是向右增长,这就使得超出定点器件数据范围所引起的误差可以忽略不计,在条件允许的前提下既可以存储32 位结果,也可以存储高16 位结果,以节约资源,也便于递推运算[4]。若只取高阶则应按Q15 进行反规格化处理,将结果除以215,2C27H/215=0.344 94;若取32 位则应按Q31 进行反规格化处理,将结果除以231,2C27C290H/231=0.344 96。将表5 中第6 行4 个AH 值相加有:1AE0+0EB8+051E+FD70=2C26H,直接舍去AL 位可简化计算,但与结果2C27H 有1个数字的误差。

表5 MAC 运算过程分解表
4 结束语
DSP 数字信号处理器的应用日趋广泛,使用定点DSP 实现小数数字信号处理算法可保证结果精确。本文详细介绍了使用定点数表示小数的方法,讨论了小数乘法运算中的几个关键问题,研究了在不同Qm.n 格式下数对数精度的影响,通过在TMS320C54x DSP 中进行小数的乘-累加运算应用实例,更深入地讨论了小数乘法的高精度运算问题。本文所介绍的方法适用于DSP、单片机、FPGA 等场合,但需要注意的是DSP 乘法器有冗余位自动消除功能,对于没有该功能的处理器在进行小数乘法操作时可通过手动方式实现,通过程序将结果向左移1 位即可。
[1]张小鸣,王正洪,朱正伟.高精度定点数平方根汇编子程序的实现原理[J].江苏石油化工学院学报,2002,14(4):59-60.
[2]余云霞,曾以成.一种有符号定点数乘法运算的快速算法[J].湘潭大学自然科学学报,2007,29(1):37-40.
[3]姚斌,陈玉涛,李静正.微机保护测控装置定点数的开方计算方法[J].电力自动化设备,2007,27(11):42-45.
[4]陈金鹰.DSP 技术及应用[M].北京:机械工业出版社,2004:129-180.
[5]邹春杰.基于软硬件协同设计平台ECNUX 的并行FFT 设计[D].上海:华东师范大学,2005.
