体部伽马刀放疗中精确靶位控制系统的仿真设计
2013-03-18张建华黑灵巧王明霞魏迎军
张建华,余 辉,黑灵巧,王明霞,魏迎军
(1.郑州大学 电气工程学院,河南 郑州450001;2.郑州人民医院 设备科,河南 郑州450003;3.黄淮学院电子科学与工程系,河南 驻马店463000)
0 引言
我国是肿瘤发病率较高的国家之一[1]. 目前治疗手段首选手术切除,但该方法存在患者痛苦、价格高、风险大等问题;而放射治疗肿瘤费用低、风险小、疗效显著,因此放射治疗逐渐成为治疗肿瘤的首选方法.采用放射法治疗肿瘤的原则是最大限度提高病变组织的射线受量和减少正常组织射线受量,因此精确放疗意义重大[2]. 在体部肿瘤的放疗中,尤其是在胸、肺、上腹部的放疗中,由于呼吸运动造成的靶位最大位移达到20 mm 左右[3],导致在放疗的过程中肿瘤周围的正常组织受到与计划受量有明显差别的辐射,从而增加了正常组织并发症的概率.因此,设计一种能减少伽马刀放疗对患者正常组织损害的系统依然是伽马刀放疗领域的研究热点.
1 设计方案
为了实现肿瘤放疗的“三精”问题,本设计系统框架如图1 所示. 由图1 可知,步进电机的控制、靶点位移模型的建立、患者呼吸信号的采集是伽马刀摆位床研究的关键. 患者在治疗时的呼吸信号被压电传感器采集后,输送给单片机系统,此时单片机会控制3 个步进电机做相应的转动,从而带动摆位床按呼吸规律的逆向进行运动,以降低呼吸对放疗精度的影响.
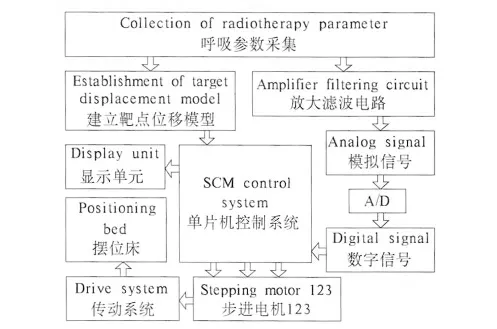
图1 智能摆位床系统的设计框图Fig.1 The design diagram of intelligent positioning bed system
1.1 硬件系统
本设计采用丝杆为滚珠螺杆(直径D =20 mm,长度L=1 m);Z1和Z2为两个传动齿轮,直径分别为d1=20 mm,d2=100 mm,宽度均为w =20 mm,摩擦系数取为μ=0.2;取病人与摆位床的重量P=120 kg;在x、y、z 3 个方向上受力Fx=1 176 N,Fy=Fz=235 N;通过计算得出负载转矩T =2.4 N·m,滚珠螺杆转动惯量I0=0.012 kg·m2,Z1和Z2的转动惯量分别为I1=0.031 kg·m2,I2=0.002 kg·m2,传动比I21=2,步进电机起动转矩Tm=8.6 N·m,考虑到其他外部因素的影响将Tm乘上一系数,在这里取a =1.5,得到步进电机起动转矩Tma=12.9 N·m.根据设计需要的速度和Tma查找步进电机选型手册,选出了SM 150 -180 -20 LFB 型号步进电机;根据步进电机的额定电流和设计的精度要求选取SA3L15C 型号的驱动器.
肿瘤运动是一个三维运动过程[4],在硬件设计中就需要将其分成三个方向的运动,并用三个步进电机分别控制. 单片机控制步进电机系统框图如图2 所示.
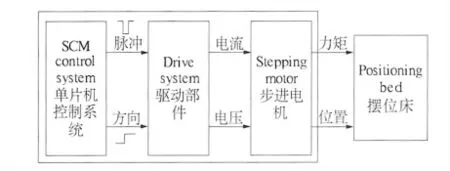
图2 单片机控制步进电机系统框图Fig.2 The block diagram of stepping motor system controlled by single chip microcomputer
SM 150 -180 -20 LFB 型号步进电机是一种将电脉冲转化为角位移的执行机构,当步进驱动器每接收到一个脉冲信号,它就驱动步进电机按设定的方向转动1.8°. 工作时,通过控制脉冲个数来控制角位移量,从而达到准确定位的目的;同时可以通过控制脉冲频率来控制电机转动的速度和加速度,从而达到调速的目的.为了提高摆位床运动的精确度,让驱动器工作在4 细分状态下,这时,步进电机每接收一个脉冲信号就会按设定的方向转动0.45°,再通过滚珠螺杆将步进电机的运动转化成直线运动,从而带动摆位床运动,降低呼吸对放疗精度的影响.
1.2 软件系统
本设计采用C 语言进行编程,在windows7 环境下利用编程软件Keil uVision3 进行编写. 软件的主要功能是控制步进电机的启动、运转方向、运行速度的变化等.
2 靶点位移模型的建立
根据伽玛刀放射治疗肿瘤的治疗要求,笔者利用CT 扫描和实时成像技术[5]获取肿瘤随着周期性呼吸运动而改变位置的横断面图像,使用插值算法重建实际的图像序列. 重建的序列可以反映出肿瘤在不同呼吸周期中的变化规律,从而得到肿瘤的偏移数据. 采用压电传感器得出患者的呼吸信号曲线.由于肿瘤的移动与呼吸同时进行,且周期相同,所以可以将两者通过时间建立起对应的关系,最后通过采集患者的呼吸信号来确定肿瘤的位移数据. 由于该患者的呼吸周期约为4.4 s,从所得数据中选取一个呼吸周期内肿瘤的44 组偏移数据.为了更加直观地检验本实验所选取的44 组偏移数据的质量,44 组偏移数据分别在x、y、z 轴的显示如图3 所示,由该图可以看出:所选取的数据能够很好地反映出肿瘤的偏移信息.
根据本设计对精确度的要求,分别采用粒子群算法(PSO)、标准差分进化算法(DE)、准牛顿算法(BFGS)和遗传算法(GA)对该实验数据进行处理,通过比较4 种算法的拟合程度及综合评估,最终选择拟合程度高、算法运行时间短的准牛顿算法,4 种算法的相关因素比较见表1.
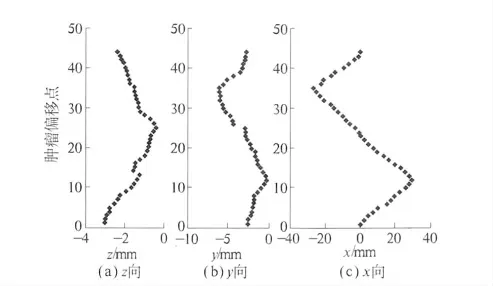
图3 44 组肿瘤偏移数据分别在x、y、z 方向上的显示Fig.3 The visual display of the 44 groups of offset datas at x、y、z directions
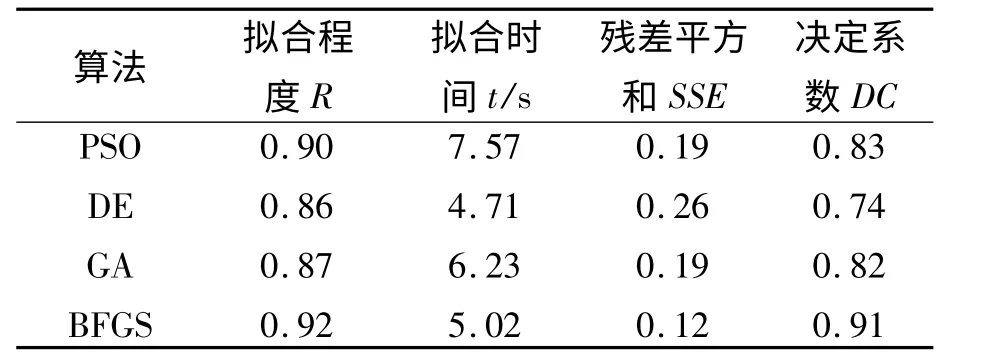
表1 4 种算法相关因素比较表Tab.1 The relevant factors comparison table of four algorithms
通过表1 可以看出:BFGS 的R、SSE、DC 均是4 种算法当中最好的,利用BFGS 算法得到的优化模型为
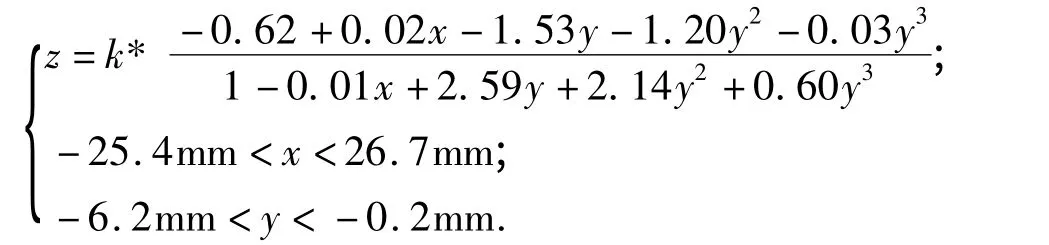
将该实验数据中的x 和y 代入上式,经过Matlab7.0 进行编程,得出z 的计算值,将z 计算值与实际z 值对比如图4 所示.由该图可看出,该模型具有很好的拟合性.
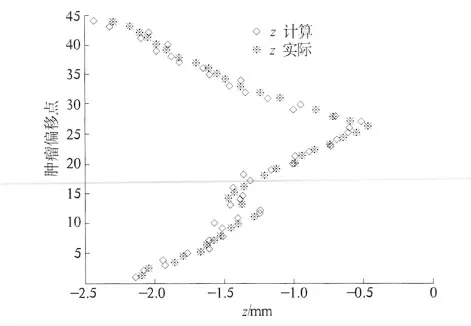
图4 BFGS 模型得出z 计算与实际z 值对图Fig.4 The comparison chart of z value obtained by BFGS model and actual z value
由于患者个体的差异性,每个患者所对应的优化模型就会有一定的差异.模型中k 为权重,不同的患者有不同的k 值.影响k 值的因素包括身高、体重、肺活量、性别、年龄等因素,导致的最终结果是肿瘤偏移数据的不同.通过更改程序中肿瘤的偏移数据,不同患者的优化模型就能很容易得到.
3 结果与讨论
使用该控制方法后,再次通过CT 扫描和实时成像技术,获得肿瘤随着周期性呼吸运动而改变位置的横断面图像,使用插值算法重建实际的图像序列.重建的序列可以反映出肿瘤在不同呼吸周期中的二维变化规律,从而得出使用控制方法后肿瘤的偏移数据(x 方向). 通过Matlab7. 0将使用控制方法前x 方向肿瘤位移数据和使用控制方法后测得x 方向肿瘤位移数据进行对比分析,如图5 所示.
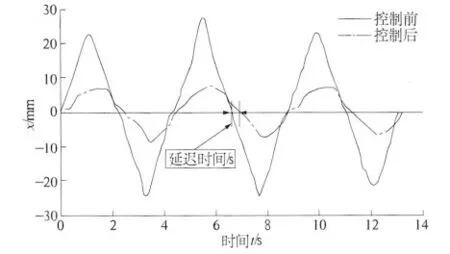
图5 x 方向肿瘤位移波形在使用控制方法前后的对比图Fig.5 Contrast diagram of tumor displacement waveform in x-axis before and after control method
图5 反映出了3 个呼吸周期中使用控制系统前、后肿瘤偏离的位移波形.实线为未使用该控制方法前肿瘤偏离的位移波形,点画线为使用了该控制系统后肿瘤偏离靶点的位移波形. 通过对比可以看出,使用该控制系统能够减少呼吸运动造成的肿瘤偏移幅度.从图5 可以看出,该系统具有一定的延迟性,分析原因主要有以下3 个方面:①单片机程序运行造成的延迟时间;②步进电机的释放信号、驱动的控制信号、方向的控制信号都需要一定的延迟时间才能有效,也造成了延迟时间;③实验时人为导致的各种误差等.同时,使用相同的方法得出y、z 方向和x 方向具有类似的结论.
4 结论
使用摆位床控制系统,能够有效地减小放疗时呼吸导致的肿瘤偏移幅度,这对减少肿瘤周围正常组织受照剂量,减少患者的并发症起到很重要的作用.但是,由于单片机系统和步进电机驱动系统都具有一定的延迟性,摆位床的运动必然会滞后于呼吸运动;用压电传感器检测到的患者呼吸信号并不与体内的肿瘤运动有相同的运动规律[6];肿瘤位移数据的采集也没有一个统一认可的方法,国内外不同学者运用不同的方法得到的肿瘤位移存在差异[7].因此,如何解决以上问题依然是国内外专家研究的热点和提高肿瘤放疗精度的关键.
[1] 郑荣寿,张思维,吴良有,等. 中国肿瘤登记地区2008 年恶性肿瘤发病和死亡分析[J]. 中国肿瘤,2012,21(1):1 -12.
[2] 任金山.浅谈中医与西医放射结合治疗肿瘤的优势与疗效[J].中医临床研究,2011,3(6):115 -116.
[3] 伍锐,陈超敏. 呼吸控制技术在肺部肿瘤精确放射治疗中的应用[J]. 生物医学工程研究,2009,28(2):159 -162.
[4] 赵军,陈健龙,张茂,等.颅内动脉瘤介入诊疗中三维旋转造影成像技术分析[J]. 中国老年学杂志,2012,32(2):241 -243.
[5] 张明鑫,王健生. 肿瘤动物模型影像学研究进展[J].中国现代普通外科进展,2007,10(6):520-523.
[6] DANIEL A,PARAG J,WEI L,et al. Novel breathing motion model for radiotherapy[J].Int J Radiat Oncol Biol Phys,2005,63:921 -929.
[7] 胡永果.探索中央型肺癌肿块位移的影响因素及其数学模型的建立[D]. 兰州:兰州大学第一医院,2010.
