伦敦奥运会男篮各队排名情况的回归分析
2013-03-16张振东蒋健涛王敏娜李鸿昕
张振东,蒋健涛,王敏娜,李鸿昕
(郑州大学体育系,河南郑州450001)
随着2012年8月12日美国和西班牙篮球比赛的结束,伦敦奥运会男子篮球比赛也画上了圆满的句号,但是篮球比赛的影响不仅仅是那短暂的半个月时间,篮球再一次在全国掀起一股浪潮,席卷篮球爱好者和篮球的研究者.本文就从奥运会男篮各队的技战术水平出发,进行详细的统计,利用逐步回归和秩相关分析各队的排名与各队的实力是否存在较大的差距,争取为伦敦奥运会男篮各队的能力做出科学的、客观的评价.
1 研究对象与方法:
1.1 研究对象
本文以奥运会男篮的比赛为研究对象进行统计分析.
1.2 研究方法
(1)文献资料法.查阅了大量的相关数据和文献资料,争取为本研究的撰写提供有力的依据.(2)录像观察法.对本次伦敦奥运会的男篮比赛进行了回放观看.
(3)数理统计法.利用SPSS16对伦敦奥运会男篮的技战术各项指标进行统计分析.
2 结果与分析
2.1 逐步回归方法在伦敦奥运会男篮技战术分析的引入
奥运会为各国竞技体育水平的展示提供了舞台,奥运会篮球比赛也是世界上篮球最高水平的赛事之一,各国篮球代表队都以得分为最主要的手段,把自身的技战术能力发挥得淋漓尽致,因此,奥运会篮球项目吸引了越来越多的眼球,影响范围也越来越大.本文从网易奥运等网站数据统计情况,对各个国家代表队技战术指标中的总投篮次数、总命中次数、投篮命中率、2分球的投篮次数、2分球命中次数、2分球命中率、3分球的投篮次数、3分球命中次数、3分球命中率、罚球次数、罚球命中次数、罚球命中率、前场篮板、后场篮板、总篮板、助攻、失误、抢断、封盖、犯规、被侵、得分等22个指标进行全面的逐步回归和秩相关分析.逐步回归是一种比较成熟的统计学方法,它是在剔除自变量间相互作用、相互影响的前提下,计算各个自变量X与因变量Y之间的相关性,并在此基础上,建立对因变量Y有最大影响的变量子集的回归方程[1].在回归方程建立以后,最主要的是确定方程中的因变量和自变量,再利用逐步回归方程进行各代表队技战术各方面实力的预测.
2.2 伦敦奥运会男篮各队实力发挥的各技术指标分析
奥运会男篮的排名主要是由各个代表队的得分能力表现出来的,能够直接反映出各个代表队的竞技水平,本文以统计的伦敦奥运会男篮22项指标进行逐一检验,将不符合的变量进一步剔除,争取建立最优化的回归模型.
对伦敦奥运会男篮的38场比赛76组数据统计指标进行逐步回归分析后,我们从得分指标剩余的21项指标中剔除了15项,它们分别是总投篮次数、投篮命中率、2分球的投篮次数、2分球命中次数、2分球命中率、3分球的投篮次数、3分球命中率、前场篮板、后场篮板、助攻、失误、抢断、封盖、犯规、被侵.而影响12支队伍得分的主要因素是:总命中次数、罚球命中次数、3分球命中次数、罚球次数、罚球命中率、总篮板这6个主要影响指标(如表1),且经过检验P<0.05,说明每个因素都具有显著的统计学意义.

表1 未标准化回归系数及标准化回归系数Tab.1 Unstandardized and standardized regression coefficients
标准回归系数能够直接反映出相关指标的影响作用,因此标准回归系数越大,其影响作用就越大,从表1可以看出:①伦敦奥运会男篮12支球队得分能力的6个主要影响程度大小的顺序依次是:总命中次数、3分球命中次数、罚球次数、罚球命中次数、罚球命中率和总篮板.②由于6个影响因素的标准回归系数均为正数,说明这6个因素与各队的实力呈正相关,在被剔除的15项指标中,总投篮次数、投篮命中率、2分球的投篮次数、2分球命中次数、2分球命中率、3分球的投篮次数、3分球命中率说明12支球队的得分意识和能力不是很强;其中的前场篮板、助攻、失误3项指标说明12支队伍的进攻意识不是很强,抢断、封盖、犯规、被侵、后场篮板5项指标说明12支球队队员的团队协作能力较弱,战术意识不强,且个人技术不够成熟.
2.3 建立各球队的得分能力情况最优化回归方程及F值检验
经检验后,由表2可以看出判定系数检验和F检验的大小,复相关系数为0.999,判定系数为R2= 0.998,说明这6项指标可以解释12支代表队大约99.8%的得分能力的变化,复相关系数代表自变量X与因变量Y之间的相关程度,它越靠近1,说明两者相关程度越高[2].调整后的判定系数为0.998,近似于1,说明这6个影响指标所建立的回归模型的拟合程度非常好.结合表1,可总结出回归方程
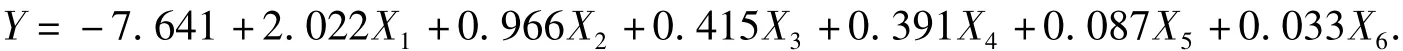
该模型就是伦敦奥运会12支男篮代表队各队得分能力的定量表达公式,其中,X1代表总命中次数,X2代表3分球命中次数,X3代表罚球次数,X4代表罚球命中次数,X5代表罚球命中率,X6代表总篮板.
表3经过F值的显著性检验,可以看到概率P值小于0.01,因此可以得出结论:各个国家代表队的得分能力Y与筛选出的6个主要影响指标的线性关系非常显著,反映各队得分能力的最优化数学模型整体设立恰当.

表2 模型拟合度检验Tab.2 Test of model degree of fitting

表3 方差分析表Tab.3 Analysis of variance table
2.4 伦敦奥运会男篮比赛名次与各队实力回归方程得分值排序情况
依据以上统计分析建立的最优化回归模型对伦敦奥运会男篮各队的得分值排序情况与积分排名进行分析,从表4可以看到,各队的实力与比赛排名呈一定的相关关系,所以本研究就以伦敦奥运会各队的比赛名次为效标,得分能力回归方程的得分排序情况与实际的排名进行秩相关分析,经检验P<0.01,所以本研究所建立的回归方程能够非常好地反映出伦敦奥运会各个代表队得分能力的主要影响因素.
根据所建立的数学回归模型,各个代表队可以根据自身队伍在比赛和训练中的表现,进行统计,将统计的数据带入回归模型进行科学的分析计算,找出自身存在的不足,教练员可以根据自身的实际情况进行训练计划的调整和制定,并能够指导球队进行主次分明、有针对性的科学训练.
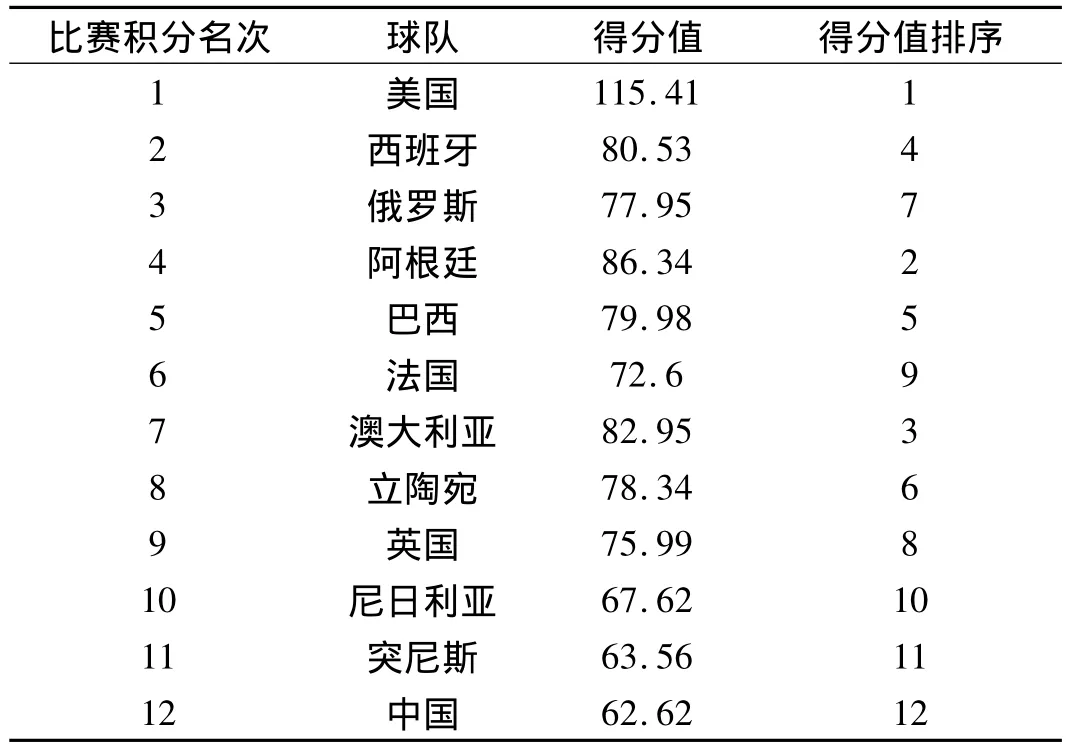
表4 各球队得分与比赛积分名次表Tab.4 Table of scores of each team and order of total scores
3 结论与建议
3.1 结论
(1)通过分析伦敦奥运会男子篮球进行的38场比赛76组数据,我们可以看到影响各球队实力发挥的因素非常多,但是经过逐步回归分析后,我们可以找出影响程度最深的六个主要因素依次是:总命中次数、罚球命中次数、3分球命中次数、罚球次数、罚球命中率和总篮板.
(2)运用逐步回归法对伦敦奥运会男子篮球赛各个代表队的技术指标数据的分析,建立拟合度很高的最优化回归方程,其时效性特别高,教练员能够根据各队的实际情况进行总结和预测,从而有针对性地、科学地安排训练内容和训练计划,进而提高各个国家运动队的水平.
(3)依据数据所建立的最优化数学模型对伦敦奥运会12支代表队得分能力的得分值排序情况与排名进行科学的秩相关分析,我们看到各个国家代表队的得分值排序与比赛积分的名次具有一定程度的相关关系,进一步证实了本研究所建立的最优化回归模型能够很好地反映出伦敦奥运会各个国家男篮的实力.
3.2 建议
(1)教练员可以根据对各个国家代表队的技战术建立的最优化数学模型,对各个代表队在比赛或者训练中所表现的各项指标进行回归分析,根据其结果找出训练的着重点,进行有针对性的训练.
(2)教练员能够根据回归方程科学地预测各个国家代表队在12支参赛队伍中的大概位置,进而制定科学的训练计划和训练目标.而且教练员也能够根据所筛选的主要影响因素来选拔有能力、有天赋的运动员,因此,该模型有助于科学选材.
(3)教练员可以根据最优化模型计算出球队的得分值,根据各个球队得分值的高低,及时发现运动队在训练和比赛中的优势和劣势,进而结合球队实际情况进行技术调整和训练,而且该模型的建立对各个国家代表队制定科学的训练计划有着重要的指导意义.
[1] 金安禄.对我校男篮参加CUBA联赛技战术运用的调查与分析[J].上海体育学院学报,1998,22(增刊):37-38.
[2] 赵利庆.影响CBA各队得分能力的回归分析[J].北京体育大学学报,2007,30(2):268-269.
