过程能力指数Cpk中的偏移系数k的正确认识

2013-03-16孙小素

山东工商学院学报 2013年6期

孙小素，何琳

(山东工商学院统计学院，山东烟台264005)

一、有偏移的过程能力指数Cpk之定义

与潜在过程能力指数Cp相比，有偏移的过程能力指数Cpk因为更符合生产过程的实际，并且通过该指标人们能够得到过程的最大不合格率信息，得到了最广泛的应用。但是，它还是一个备受争议的指数，争论的焦点集中在Cpk能否为负值。根据 Cpk的定义(见式(1))，由于 Cp＞0，因此，Cpk能否为负值的实质又是k能否大于1的问题。针对这一问题，质量管理界形成了4种观点——荒谬论，不可能论，限定范围论和k的定义错误论。4种观点莫衷一是，甚至截然相反，对人们正确使用和解释Cpk造成了困惑，必须予以澄清。

对于Cpk能否为负值，也即k能否大于1，之所以存在众多的争论，原因就在于人们还没找到一种有效方法，对k的取值范围给出令人信服的界定。笔者尝试利用控制图技术解决这一问题。

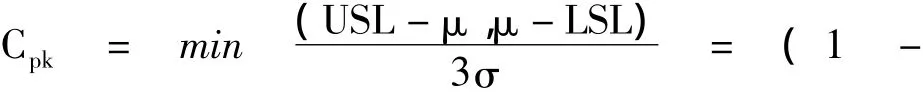
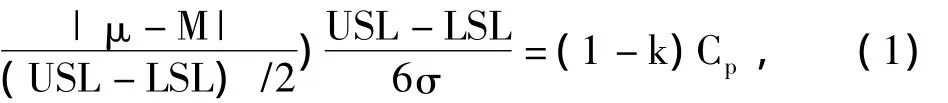
过程能力指数 Cpk的定义是［1］:式中，USL(Upper Specification Limit)表示质量特性的上规格限;LSL(Lower Specification Limit)表示质量特性的下规格限;表示偏移系数;表示潜在过程能力指数;M=(USL+LSL)/2表示规格中心(公差带中心)。

二、目前质量管理界关于Cpk＜0或k＞1的主要看法

归纳起来，目前质量管理界关于这一问题主要形成了4种观点。

(一)荒谬论

代表人物是张公绪先生。他们认为，Cpk＜0或k＞1十分荒谬。张公绪在其所著的《两种质量诊断理论及其应用》不止一次讲到［2］，“当μ=TU(笔者注:TU对应于本文的规格上限USL)或μ=TL(注:TL对应于本文的规格下限LSL)时，k=1，CpK=0，实际上，这时合格品率仍为50%，故Cpk=0是不恰当的，不得已只好加上这样的说明:‘Cpk=0表示过程能力由于偏移而严重不足，需要采取措施加以纠正’。当μ位于公差界限之外时，k＞1，Cpk＜0，这简直是荒谬，故此时硬性规定Cpk=0。这说明Cpk的定义不完善，只能用于偏离量ε不太大(注:ε对应于本文的|μ -M|，即 ε =|μ -M|)，即k＜1的场合。”

从张公绪先生对Cpk取值情况的探讨看，他认为过程能力指数的取值不超过零时过程尚有合格率(甚至可能达到50%)，这种数量对应关系是荒谬的。在他看来，当这些指数为零时，过程的不合格率也应为零。严格来讲，他并没有否定Cpk＜0或k＞1的可能性，甚至暗含着Cpk有可能小于零，或者k有可能大于1，不然也就不需要硬性规定，更不需要对这种硬性规定不满了。

(二)不可能论

代表人物是何晓群教授。他认为，Cpk不可能小于零，或者说k不可能大于1。何晓群教授从两个方面论证了Cpk＜0或k＞1是不可能的［3］。其一，当偏移量 ε=T/2时，k=1，则 Cpk=0，远远低于0．67，更低于最小可接受值1．33。此时过程能力已经严重不足，应采取紧急措施进行全面检查，必要时停工整顿。在生产现场根本等不到过程能力低下到这种程度，现场的种种异常现象早已警示操作者停工检查。再说就算偏移量ε=T/2(T=USL-LSL表示规格范围)可以达到，偏移量ε=T也是不可能达到的。因此偏移量ε的取值范围是:0≤ε≤T/2。其二，对过程能力的考察，不会间隔相当长的一段时间才测量的，这样数值相差很大，而是在一个班次中测量多次，用来监控生产过程是否正常。也就是说每相邻两次测量的过程能力指数不会使过程能力评定等级相差两个及其以上的级别差，即上一次测量的过程能力指数级别是II，而这一次的测量级别是IV，或者更差。当过程能力指数低于最小可接受值1．33时，企业就会进行生产过程微调，使过程能力指数不低于最小可接受值1．33。

(三)限定范围论

这种观点多见于国外学者的研究报告［4-5］。他们在研究Cpk时，只是简单地把k限定在［0，1］，并不说明原因。

(四)k的定义错误论

严格的说，这类观点并不是针对Cpk或k的取值范围的，但却是由此引起的。持这类观点的主要有3个代表性人物。一个是青岛海信智能商用设备有限公司的高级研究员宋祥彦，另一个是上海理工大学管理学院的郭进利老师，还有一个就是北京工业大学的于善奇教授。他们都对已有的Cpk公式提出了质疑和改造，但改造的依据和方式却不尽相同。其中，宋祥彦和郭进利两个人的共同点是，他们都坚信Cpk＜0或k＞1十分荒谬，但对待Cpk或k的方式却不同。宋祥彦的处理方式，用他自己的话说就是［6］，“在张教授的启发下，对过程能力指数基本概念和理论进行了系统研究，发现了过程能力指数的四个基本特性;在此基础上分析和解剖了Cpk公式的错误表现形式及其错误本质…;提出了正确的Cpk公式并进行了证明…”他通过改造k实现了对Cpk的改造。他认为，有偏移过程的偏移系数应定义为ε/T，相应的过程能力指数应定义为(T-ε)/6σ。若记宋祥彦的偏移系数为k'，则有k'=k，C=(1-k')C=(1pkrp-k)C(C是宋祥彦本人给出的记法，笔者ppkr注)。郭进利从解决“质量管理中出现的‘直观悖论’:当k=1时，Cpk=0，而合格品率还接近50%”(显然，郭进利所说的质量管理中出现的“直观悖论”就是张公绪先生所说的荒谬论)入手，将现有的Cpk公式改造为:¯Cpk=Cp/(1+k)3，并指出，他的改造式的特点是［7］，“k增大，¯Cpk减小，且当k=0时，¯Cpk=Cp;当k=1，即过程中心与规格界限重合时，合格率仍接近50%，但¯Cpk≠0，而且这时¯Cpk的量相当于理想状态下(指过程中心μ与规格中心M相重叠，笔者注)合格率接近50%所对应的Cp;当过程中心(过程特性值的分布均值)偏离公差中心(指规格中心M，笔者注)非常大时，¯Cpk≈0，合格品率也接近于0。”与前面这二位不同的是，于善奇教授研究的出发点并非张公绪先生所说的荒谬论，他的矛头直指k的定义。他指出［8］，“当工序有偏时，式(1)的定义是有缺陷的，其缺陷在于:偏移系数定义为是不合理的。这是因为在实际的生产过程中，分布中心μ对规范中心M而言，除无偏外，非左即右，二者必居其一。偏移量是对规范中心而言，故偏移量的定义是合理的。偏移系数应该是偏移量ε对公差幅度T而言，即偏移系数定义为ε/T更加科学、合理。如果把定义为偏移系数，则只能理解为偏移量对半个公差而言，这显然是不合理的。”虽然出发点不同，于善奇教授对k的改造及由此得到的Cpk的公式，却与宋祥彦的结论不谋而合。

从上面的介绍看，学者们对Cpk(或k)的取值范围莫衷一是，甚至截然相反，如何正确评价、合理取舍学者们的观点呢?这显然需要更深一步的剖析。

三、Cpk＜0或k＞1究竟意味着什么?

直观上看，Cpk＜0首先意味着过程能力很低，过程生产的合格率很低，其根本原因是过程的输出中心μ偏离规格中心M太远(远到k＞1)。这种显而易见的结论显然不需要再研究，在此，笔者想借助控制图对k的取值范围进行深入探讨。

(一)可以用来检测过程输出中心发生偏移的控制图

产品的质量特性具有变异性，但是这种变异并非杂乱无章，而是有一定的规律可循。经验与理论分析表明，当生产过程中只存在随机因素时，产品质量特性值将形成某种典型分布，如具有特定参数的正态分布。如果除去随机因素外还有系统因素，则产品质量特性值的分布必将偏离原来的典型分布。因此，根据典型分布是否被偏离就能判断出有无系统因素的存在。控制图就是利用变异的这一统计规律设计出来的统计假设检验的图上作业法。具体地讲，将按一定顺序抽取的样本统计量数值，描在有中心线(CL)和上、下控制界限(UCL，LCL)的图上，形成一个序列图(示意图见图1)。观察该序列图，若控制图中的描点落在上、下控制界限之外，或描点在上下控制界限之间的排列不随机，则表示过程出现了系统因素，并引起过程的异常。能引起过程中心发生位移的一定是系统因素，因此如果相应的控制图显示出异常，那很有可能过程中心发生了位移。一旦过程中心发生位移，那就必须采取措施加以排除，使过程中心回到原来的位置上去。

对于计量质量特性而言，存在两大类控制图——常规控制图和累积和控制图。其中，常规控制图主要用来检测控制对象大的偏移，而适用于检测平均水平有无大的偏移的常规控制图主要有两张，一张是单值控制图，另一张是均值控制图;累积和控制图主要用来检测控制对象中、小程度的偏移，可以检验均值有无中、小程度偏移的是均值累积和控制图。

(二)控制图中的判异准则及对应事件的概率

根据质量特性波动的原理，如果质量特性的分布中心没有发生位移，则其波动不会太大，换言之，如果波动太大，那就意味着过程的分布中心发生了偏移，那么这个界限该如何划定呢?

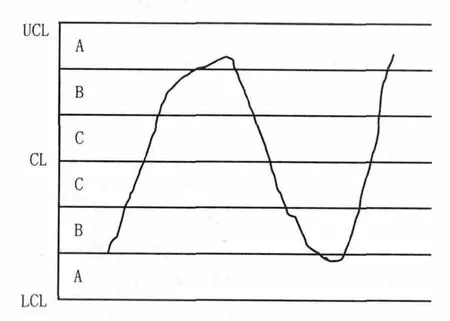
图1 控制图示意图

国家标准《常规控制图》依据把第一类错误α(即虚发警报的概率)严格控制在0．27%(这就是著名的3σ原则)以内，同时适度控制第二类错误β(即漏发警报的概率)的原则，规定了8条判定异常的准则［9］，并指出这些准则适用于均值(¯x)控制图和单值(x)控制图。其具体内容为，准则1:一个点落在A区以外;准则2:连续9点落在中心线同一侧;准则3:连续6点递增或递减;准则4:连续14点中相邻点上下交替;准则5:连续3点中有2点落在中心线同一侧的B区以外;准则6:连续5点中有4点落在中心线同一侧的C区以外;准则7:连续15点落在中心线两侧的C区内;准则8:连续8点在中心线两侧，且无一在C区中。

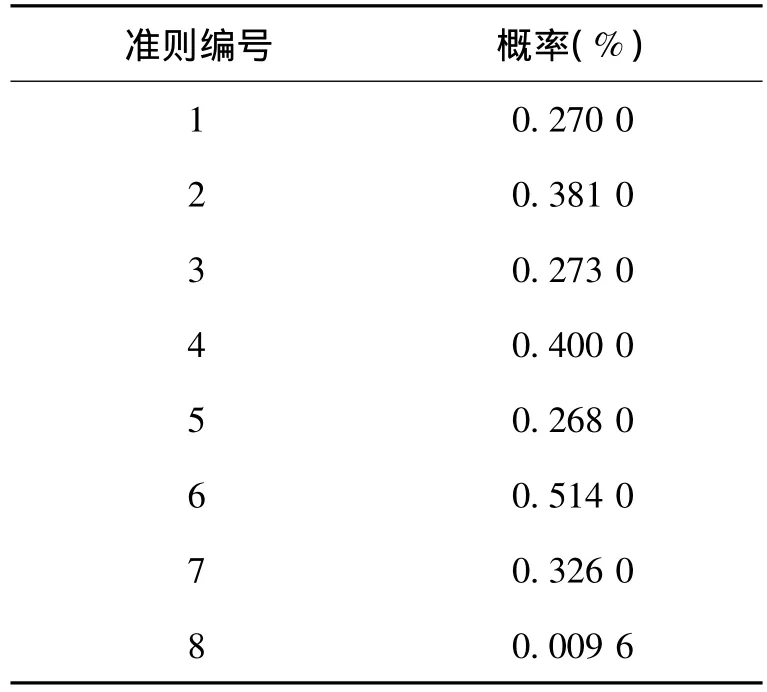
表1 判异准则对应事件发生的概率

笔者测算了这8条判异准则对应事件的概率［10］，列入表 1。

从表1中不难发现，判异准则规定的随机事件在原假设成立(即过程处于统计控制状态)时，发生的概率都很小，所以，一旦当均值(¯x)控制图和单值(x)控制图上显示这些小概率事件出现时，即判断过程发生异常。

仔细研究一下这8条判异准则，笔者发现，其中的第1，2，3，5，6条都是针对过程的分布中心有无偏移(位移)的，可见常规控制图对分布中心位移导致的异常波动还是非常重视的。

累积和控制图设计原理与常规控制图不同，它利用以往所测得的所有观测值信息的总和，作为控制图上的一个点，故“异常”的判断是利用了以往所抽取的样本的全部信息，因此，具有灵敏度高、控制可靠(可检测出中、小程度的偏移)等优点。还有一点与常规控制图不同的是，它通过链长这一工具，可以同时控制犯第一类错误和第二类错误的概率，这也是它优于常规控制图的地方。该图对异常的判断有两种方法——V形模板法，以及有判定距的固定界限控制图法［11-14］。

(三)控制图可以把k控制在什么范围?

在质量管理中，通常用μ0表示可接收的均值，相应于能使所生产的产品获得最好质量的工艺状态(显然它就是公差带的中心值M);μ1表示拒收的均值，是被检质量特性所允许的极限均值，超过它就要求对过程进行校正;δ表示过程异常时所规定的经标准化的位移量的绝对值，其定义是:

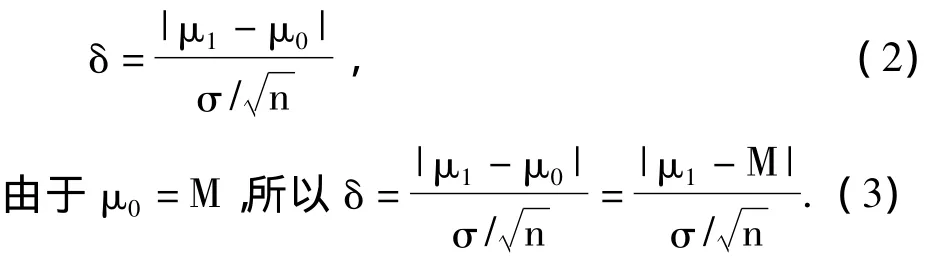
1．单值(x)常规控制图中δ的临界位移量值及对应的k的取值范围

这里，临界偏移量值是指过程正常波动和异常波动的分界线。通过上面的介绍，我们知道，对于单值(x)常规控制图，则:

即若选择单值(x)常规控制图来控制过程输出中心的理想值μ0(=M)，则δ等于3时一定会报警过程失控。不仅如此，如果控制图上出现了判异准则2，3，5，6规定的情形，则等不到δ达到3就会报警过程失控。因此，单值(x)常规控制图中δ的最大临界位移量值即为3。此时，k会取什么值呢?

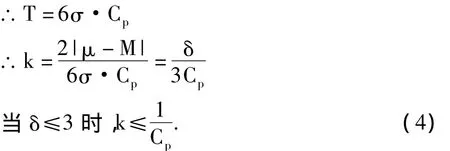
这就是说，一旦报警过程不处于统计控制状态，那么k绝对不会超过1/Cp，至于它会不会超过1而导致Cpk＜0，则完全取决于Cp。在当今经济全球化背景下，企业之间的竞争只会越来越激烈，对Cp提出1．33的最小可接受值一点也不过分，此时，如果企业使用单值控制图，则k≤0．75。也就是说，正常情况下，k不会超过1，因此Cpk也不会小于0。

k与Cp之间的这种数量关系很有价值。在企业的质量管理中，常用Cp表示质量能力，k表示管理能力，可以想象，这两种能力之间应该会相辅相成，没想到他们之间竟会存在这样严格的数量关系，毫无疑问，这种数量关系将为企业实施精细化管理提供科学依据。

2．均值(¯x)常规控制图中δ的临界位移量值及对应的k的取值范围

同理，对于均值(¯x)常规控制图，则:

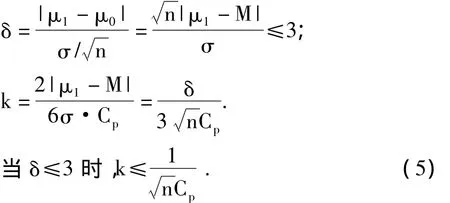
式(5)表明，如果使用均值(¯x)常规控制图控制的分布中心发生位移，那么最大偏移系数将取决于样本量和过程的质量能力两个因素。国家标准 GB/T 4091-2001 在10．4 中明确指出［9］:通常子组大小取为4或5，并说明这种规定是遵循合理子组原则的产物。合理子组原则是指，过程变动(shift)在取样期间发生的机会要最小(因此要采用小样本)，在两次取样之间发生的可能性最大(因此要至少取25个子样)，如果变动注定要发生的话。因此，如果 n=4，Cp=1．33，那么 k≤0．375;如果 n=5，Cp=1．33，那么 k≤0．336。即，如果企业使用均值(¯x)常规控制图，通常情况下，k连0．5都不会超过，因此Cpk也绝不会小于0。

比较式(4)与(5)，我们发现，在其他条件相同时，单值控制图对异常的检出力只是均值控制图的 1 /，因此，除非我们取得数据实在困难，或者取样期间过程的均匀性非常好，最好不使用单值控制图监控过程的位移。

3．均值(x¯)累积和控制图中δ的临界位移量值及对应的k的取值范围

与常规控制图将临界位移量控制在3之内不同的是，均值累积和控制图可将标准位移量控制在0．5～2．5之间［15］。文献［15］又具体给出了 δ 的三种临界位移量值标准——δ ＜0．75，0．75≤δ≤1．5，δ＞1．5。下面探讨这三种情形下k的取值。

与探讨均值(x¯)常规控制图下k的取值范围相类似(过程略)，我们很容易得到:(1)当 δ＜值累积和控制图的最大标准位移量不超过2．5，因

给定 n=4，Cp=1．33，对应于 δ ＜0．75，有 k ＜0．093 75;对应于0．75≤δ≤1．5，有0．093 75≤k≤0．187 5;对应于 1．5 ＜ δ≤2．5，有 0．187 5 ＜ k≤0．312 5。我们不再计算 n=5，Cp=1．33 时各种临界位移量值对应的k值了，但有一点可以肯定，那就是k一定小于0．312 5。

综上所述，只要企业使用均值累积和控制图，通常情况下，k同样连0．5都不会超过，因此Cpk也绝不会小于0。

(四)Cpk＜0或k＞1究竟意味着什么?

通过上面一系列的研究和分析，现在我们可以肯定地说，正常情况下，k不会超过1，因此Cpk不会小于0，除非:第一，企业没有进行任何形式的过程控制。我们在前面已强调，过程处于统计控制状态是企业研究过程能力指数的先决条件，为此必须进行过程控制，否则我们只能对计算的结果茫然失措，不知作何解释;第二，用Cp表示的企业的质量能力十分低下。对于均值累积和控制图而言，要使 k＞1，Cp甚至最低不会超过 0．125;对于单值控制图而言，也要Cp小于1。这种情况下，虽然有控制图保驾护航，但由于Cp过小，隐含其背后的是过程波动过大，即使过程处于统计稳态，但由于达不到技术稳态(至少要求Cp≥1．33)，这样的企业同样是无法生存的。

四、重新审视学术界关于Cpk＜0或k＞1的主要观点

(一)荒谬论成立的条件是非常苛刻的

原因有两个:其一，Cpk有可能小于0，或者 k有可能大于1的说法不是没有一点道理，只是这种可能性在非正常情况才会成为现实。只要企业开展质量控制活动，并且质量能力没有低到让人无法接受的地步，这种情况就不会发生，因此对Cpk会小于0的担心缺乏理性;其二，Cpk的取值不超过零时过程尚有合格率(甚至可能达到50%)，这一数量关系也被郭进利称为“质量管理的‘直观悖论’”，我们说这种数量对应关系并不荒谬。通过对过程能力指数的介绍，我们知道，合格率就是随机事件LSL≤X≤USL发生的概率，只要企业组织生产，这个概率就是客观存在的，它可能大，也可能小，但绝不可能小于等于0;Cpk是我们定义出来的一个指标，从Cpk=(1-k)Cp的定义公式看，它是k与Cp综合的产物，它的正负完全取决于k是否大于1，我们在定义 k时并没有限定 μ∈［LSL，USL］，因此从数理角度讲，k当然可以取大于等于1的值，而当k≥1，也即Cpk≤0时，对应于随机事件LSL≤X≤USL的概率还是P=Φ［3(1-k)Cp］+Φ［3(1+k)Cp］-1，这种对应关系是客观存在的。如果我们非要挑出点毛病的话，那是不是可以说过程能力指数这个名字起得不合适，因为根据我们的理解习惯，给一个冠之以“能力”的指标一个负值确实令人费解。

(二)不可能论具有现实基础，但论证过程有失严谨

笔者通过大量的数学论证，得到了只要企业具有过程控制措施，且 Cp＞1．33，才有 k≤0．75的结论。当然，如果一个结论是显而易见的，或许并不需要我们这么大费周折，可事实并非如此，这从笔者的研究过程就可看出来。另外，不可能论者之所以把问题简单化，还在于他的一些想当然的看法。其一，把基于Cp的过程能力评级简单地等同于基于Cpk的过程评级。这一点在他的论述中是显而易见的［3］。根据过程能力指数的不同取值对过程能力划分等级，得到了大家的一致认可，但其依据是潜在过程能力指数Cp，这一点你在任何一个介绍潜在过程能力指数的文献中都会发现。何晓群教授依据“Cpk=0，远远低于0．67，更低于最小可接受值1．33”的判断显然是不严谨的。我们不能单单依据一个Cpk就做出过程是否有能力还有一个理由。我们知道，Cpk是k与Cp综合的产物，但在实际中对待k与Cp的态度是不同的，经验表明，改变平均值(即改变k)会比减少标准差(即改变Cp)更为容易，因此，我们既需要将Cpk作为一个整体来对待，更需要将其拆为k与Cp来分析，这样得到的结论才更客观，提出的措施才更有针对性。这一点其实也是何晓群教授在文献［3］中表达的看法。其二，何晓群教授所谓的“就算偏移量ε=T/2可以达到，偏移量ε=T也是不可能达到的”依据又是什么呢?

(三)限定范围论有失严谨

国外学者对Cpk进行相关研究时，或许是限于篇幅，加之研究的重点并非是Cpk的取值问题(根据笔者的搜索，国外尚无这方面的专门文献)，他们只是简单地把k限定在［0，1］范围之内。根据前面的论证，k在0到1之间并非不言而喻的，因此，就一个公式定义而言，这种做法有失严谨。

(四)k的定义错误论有待进一步商榷

首先来看郭进利的观点。实事求是地讲，他并没有说k的定义是错误的，而只是从“质量管理的‘直观悖论’”入手，从数学角度解决了所谓的“直观悖论”。我们在前面已经讨论了并不存在“质量管理的‘直观悖论’”，因此也就无需解决这一问题。宋祥彦也是从“质量管理的‘直观悖论’”入手，通过长期的潜心研究和不懈探索，发现了过程能力指数定义所隐含的4个推论和4个基本性质，从多个角度论证了k的定义是错误的，他认为正确的偏移系数应该是现在的1/2。这里先不讨论他对k的重新定义是否正确，单就他想要解决的所谓的“质量管理的‘直观悖论’”角度讲，他只是缓解了所谓的“直观悖论”(在相同条件下，他只是降低了Cpkr=0时的不合格率，但并未将它降至0。这里Cpkr是他重新定义的有偏移的过程能力指数)，并未真正解决之。因此，从他研究的出发点而言，可以说他并未成功。于善奇教授虽没说他相信存在“质量管理的‘直观悖论’”，但对k的改造却与立志要解决所谓的“直观悖论”的宋祥彦不谋而合，让人不得不怀疑现在的偏移系数是否真的定义错了?笔者经过慎重思考后还是觉得现在的偏移系数的定义并不错，其原因就在就在于善奇教授本人的解释中。让我们再仔细读读他将偏移系数由改造为ε/T的原因:“当工序有偏时，式(1)的定义是有缺陷的，其缺陷在于:偏移系数定义为是不合理的。这是因为在实际的生产过程中，分布中心μ对规范中心M而言，除无偏外，非左即右，二者必居其一。偏移量是对规范中心而言，故偏移量的定义是合理的。偏移系数应该是偏移量ε对公差幅度T而言，即偏移系数定义为ε/T更加科学、合理。如果把定义为偏移系数，则只能理解为偏移量对半个公差而言，这显然是不合理的。”我们知道，定义相对指标的一个原则就是分子、分母的口径要一致，既然分子“非左即右，二者必居其一”，那么分母为什么要把左右全部算进来呢?

［1］Kane V E．Process capability indices［J］．Journal of Quality Technology，1986，18(1)，41-52，．

［2］张公绪．两种质量诊断理论及其应用［M］．北京:科学出版社，2001．

［3］何晓群．关于过程能力指数公式的几点辨析［J］．数理统计与管理，2008，(6):1066-1071．

［4］A Parchami，M Mashinchi．Fuzzy estimation for process capability indices［J］．Information Science，2007，(177):1452-1462．

［5］Zachary G Stoumbos．Process capability indices:overview and extensions［J］．Nonlinear Analysis:Real World Application，2002，(3):191-210．

［6］宋祥彦．六西格玛管理质疑［M］．青岛:青岛出版社，2005．

［7］郭进利，赵彦云．新的过程能力指数［J］．系统管理学报，2008，(2):116-120．

［8］于善奇．工序能力指数的新定义及其应用［J］．世界标准化与质量管理，2007，(1):53-54．

［9］全国统计方法应用标准化委员会．中华人民共和国国家标准《常规控制》［S］．北京:中国标准出版社，2001．

［10］孙小素，杜一哲．国家标准《常规控制图》判异准则的问题及其改进［J］．统计与信息论坛，2009，(12):19-25．

［11］约瑟夫·M·朱兰，A·布兰顿·戈弗雷．朱兰质量手册:第五版［M］．焦叔斌，译．北京:中国人民大学出版社，2003．

［12］于振凡．最新统计抽样检验与过程控制［M］．北京:中国标准出版社，2004．