广义线性互补问题的极大熵牛顿算法

王爱祥



广义线性互补问题的极大熵牛顿算法

王爱祥

(常州广播电视大学信息与工程学院，江苏，常州 213001)

借助一类特殊的绝对值方程，将广义线性互补问题等价转化为非线性方程组。基于极大熵函数，提出了一个牛顿算法，证明了算法的局部收敛性。数值结果也验证了算法的有效性。

广义线性互补问题；绝对值方程；极大熵；牛顿算法

0 引言

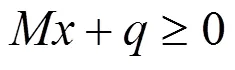
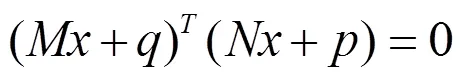
广义线性互补问题（1）经常出现在偏微分不等式的有限差分法求解中，非线性网络，控制理论以及机械工程应用方面。同时，它也是经典的线性互补问题

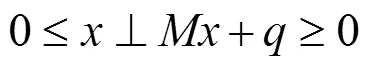
的一个扩展。文献[1]研究了广义线性互补问题（1）解的存在性。文献[2]建立了广义线性互补问题（1）的无约束优化问题的转化形式，并用下降算法来求解。文献[3]给出了一个信赖域算法来求解广义线性互补问题（1）。文献[4]给出了非光滑的L-M算法，在适当条件下，证明了算法的全局收敛性。

本文不同于以往算法，而是将广义线性互补问题（1）转化成一个新的绝对值方程组，并且建立了一个牛顿算法来求解。

1 广义线性互补问题的解

下面给出广义线性互补问题唯一可解的充要条件。根据定理3[1]有

引理1.1对任意，，广义线性互补问题

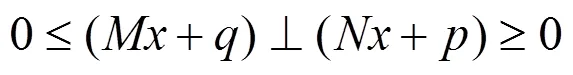
定理1.1 广义线性互补问题（1）等价于绝对值方程

证明 考虑每一个分量，根据

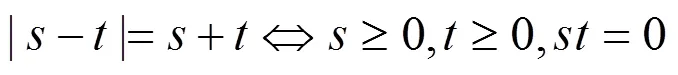
可知广义线性互补问题(1)等价于

证毕。

由定理1.1可知，广义线性互补问题（1）可以转化为绝对值方程（1.1）来进行求解。

2 极大熵函数

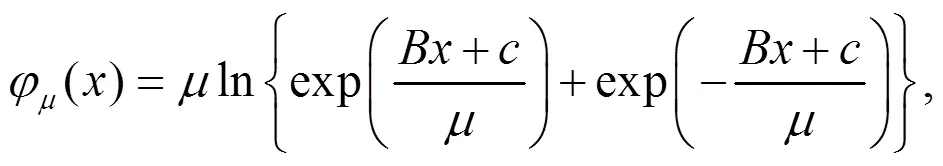
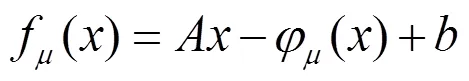
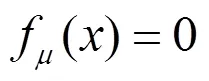
的解就是绝对值方程（2.1）的解且

证毕。

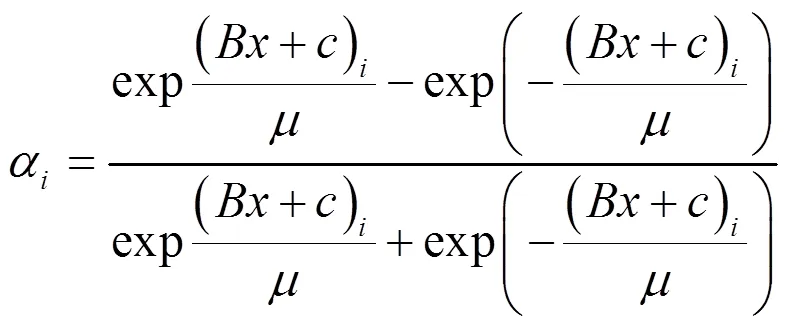
3 牛顿算法及其局部收敛性

下面给出牛顿算法进行求解。

算法3.1

步骤1 计算

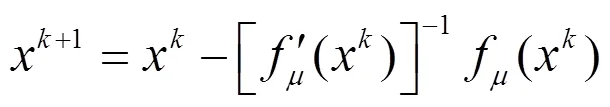
下面分析算法的收敛性和收敛速度。

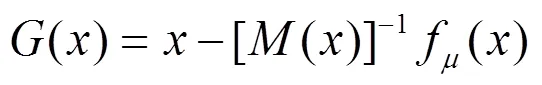
引理3.1 证明类似于文献[7]，此处省略。

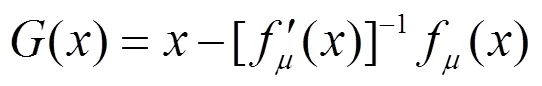
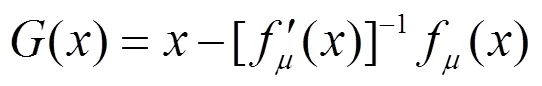
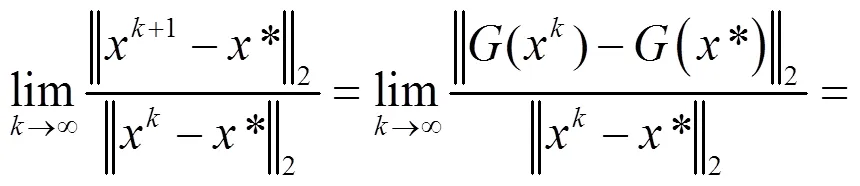
证毕。

4 数值算例

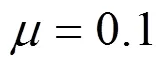
例1（随机测试）求解广义线性互补问题

随机生成初始向量

迭代结果为

运算结果表1所示。

表1 计算结果

Table 1 Computing result

考虑数值精度，计算

可见，算法提高了数值的精度。这也说明了算法的有效性。

本文基于极大熵建立了求解广义线性互补问题的一个牛顿算法，证明了算法的收敛性。然而，算法过程中涉及到矩阵求逆，因此初始点的选取还有一定的要求。同时，算法仅能保证局部收敛。如何构造全局收敛的有效算法有待于进一步思考与研究。

[1] 张超, 修乃华. 关于扩张的垂直线性互补问题的V-P性质[J]. 北方交通大学学报, 2003,27(6): 86-91.

[2] Tseng P, Yamashita N, Fukushima M. Equivalence of complementarity problems to differentiable minimization: A unified approach [J]. SIAM J Optim, 1996, 6:446-460.

[3] Jiang H, Fukushima M, Qi L, Sun D. A trust region method for solving generalized complementarity problems [J]. SIAM J Optim, 1998, 8:140-157.

[4] Wang Y, Ma F, Zhang J. A nonsmooth L-M method for solving the generalized nonlinear complementarity problem [J]. Appl Math Optim, 2005, 52:73-92.

[5] 邓永坤，张萍. 绝对值方程的光滑牛顿算法 [J]. 黑龙江科技学院学报, 2011, 21(6): 499-502.

[6] 李兴斯. 一类不可微优化问题的有效解法 [J]. 中国科学:A辑, 1994, 24(4): 371-377.

[7] 李庆扬,莫孜中,祁力群. 非线性方程组的数值解法[M]. 北京:科学出版社, 1987: 8-50.

MAXIMUM ENTROPY NEWTON ALGORITHM FOR GENERALIZED LINEAR COMPLEMENTARITY PROBLEM

WANG Ai-xiang

(School of Information and Engineering, Changzhou Radio and Television University, Changzhou, Jiangsu 213001, China)

The generalized linear complementarity problem is converted to nonlinear equations by a specialized case of absolute value equations. Based on the maximum entropy function, the Newton method is established and the convergence of maximum entropy Newton method is studied. Numerical results imply that the algorithm is effective.

generalized linear complementarity problem; absolute value equations; maximum entropy; Newton method

1674-8085(2013)02-0025-03

O242.2

A

10.3969/j.issn.1674-8085.2013.02.005

2012-10-06；

2013-01-18

王爱祥(1984-)，男，江苏兴化人，助教，硕士，主要从事计算数学研究(E-mail: wax84@163.com).