基于正位移解的DELTA机器人工作空间分析
2013-03-15胡如方
彭 煜,高 洪,陈 啸,蒋 璇,胡如方
基于正位移解的DELTA机器人工作空间分析
彭 煜,*高 洪,陈 啸,蒋 璇,胡如方
(安徽工程大学先进数控与伺服驱动技术安徽省重点实验室,安徽,芜湖 241000)
针对DELTA并联机器人,基于空间机构学理论和矢量法,建立该并联机构位移模型,给出其正、逆向位移解数值求取方法,提出基于正位移解的工作空间分析方法,采用MATLAB软件进行了仿真,为DELTA机器人的轨迹规划奠定了良好的基础。
DELTA机器人;位移模型;正位移解;逆位移解;工作空间
0 引言
Clavel教授于1985年提出的空间三自由度DELTA并联机构,是目前设计最成功、应用最广泛的并联机构之一[1-4]。其运动简图如图1所示,由静平台(上部平台)、动平台(下部平台)、三根主动杆(驱动杆)、三个从动支链(平行四边形闭环)组成,基座静平台通过三条相同的运动链分别连接动平台的三边来传递运动,每条运动链由一根驱动杆和一个由四个球铰和杆件组成的平行四边形闭环组成,驱动杆与平行四边形闭环通过转动副连接,三组平行四边形闭环机构保证了静平台与动平台的平行关系,使动平台不能绕任何轴旋转,只保留了平动功能。根据空间机构自由度计算通式可得DELTA型机器人具有三个自度,简单紧凑的结构赋予其良好的运动学和动力学特性。
针对DELTA并联机构,赵杰教授运用空间几何学方法给出了其运动学正解[1];C. Szep等采用基于逆解的数值方法,研究了其定姿态的位置空间[3]。本文则基于空间机构学理论[5]推导DELTA并联机构空间运动位移方程,又运用Matlab软件编程[6],实现其正、逆向位移解求取的程序化,然后,基于正位移解确定DELTA型机器人的工作空间,最后,对所求工作空间中任意点进行了逆解程序验证。
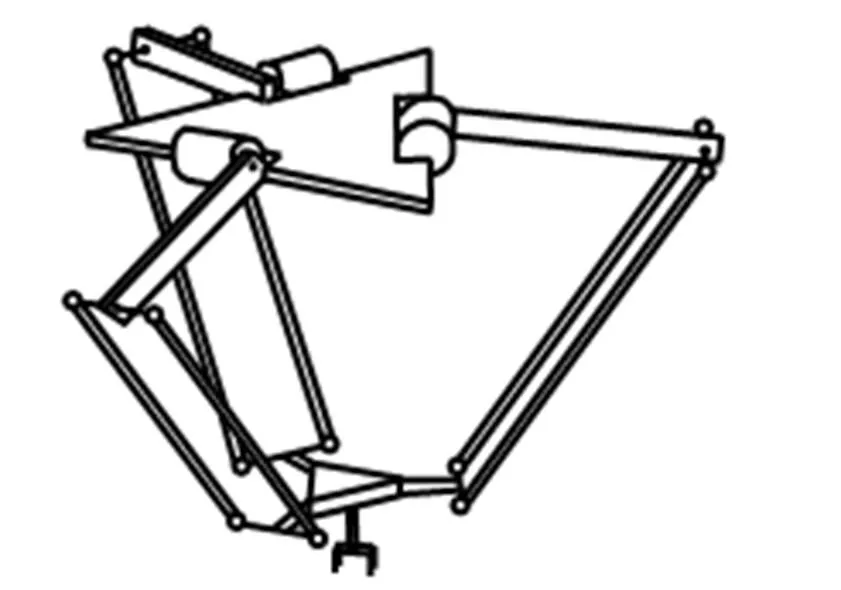
图1 DELTA机器人结构简图
1 DELTA机器人的运动学模型
1.1 DELTA机器人的位移方程
为方便求取静、动平台位置关系,将机构简化,在平行四边形闭环上下两边的中点之间,加入三根虚拟连杆,由于动平台只有平移运动没有转动,即 相对于静平台的姿态固定,所以机构中各支链的平行四边形闭环不会发生扭曲。在这种情况下,平行四边形左右两边的运动,可以用其上下两中点连线的运动代替,简化结构如图2所示。
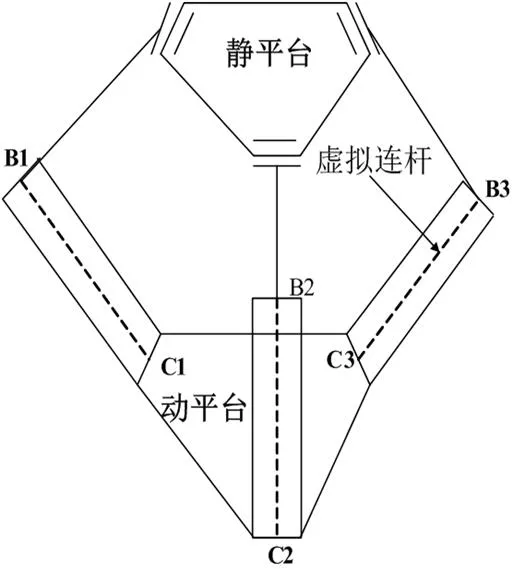
图2 简化后的DELTA机构
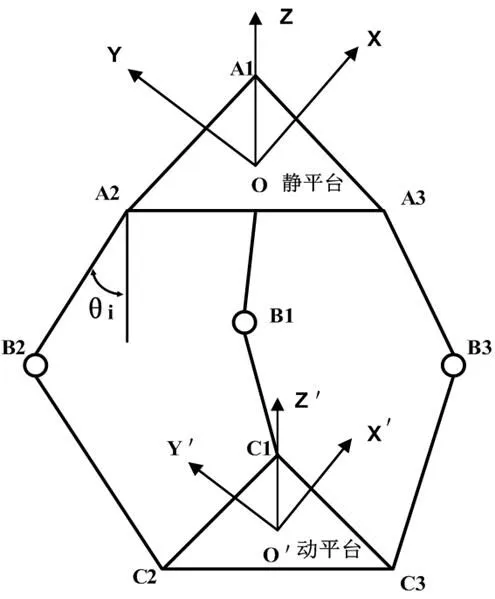
图3 静、动平台坐标系
在简化后的模型基础上,建立静、动平台坐标系,如图3所示,以静平台中心O点为坐标原点建立静坐标系O-XYZ,动平台中心O¢点为坐标原点建立动坐标系O¢-X¢Y¢Z¢,AiBi(i=1, 2, 3)为三根驱动杆,长度为L1;BiCi(i=1, 2, 3)为三根从动杆,长度为L2;qi(i=1, 2, 3)为三根驱动杆相对于静平台的张角;OX与O¢X¢分别垂直于OA3和O¢C3, 静平台上OAi与X轴的夹角为hi(i=1, 2, 3),如图4所示。
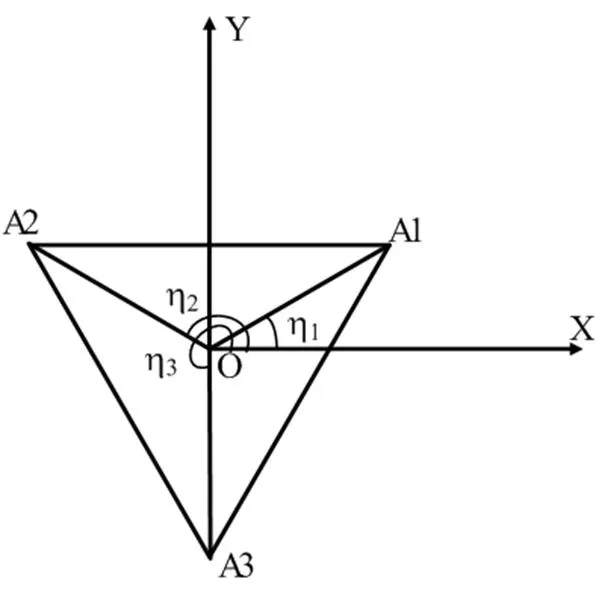
图4 静平台X-Y坐标系
确定静、动平台的结构参数,令|OAi|=R,|O¢Ci|=r, 则Ai点在静平台坐标系O-XYZ中的位置矢量和Ci点在动平台坐标系O¢-X¢Y¢Z¢中的位置矢量分别为:
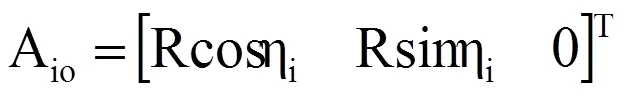
其中,h1=p/6,h2=5p/6,h3=3p/2;
利用几何关系,将Bi点的位置矢量在静平台坐标系O-XYZ中表示出来,
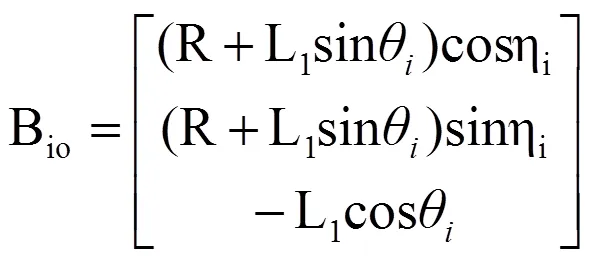
假设矢量OO¢在坐标系O-XYZ中的表示为O¢o=[]T,则矢量OCi可以表示为:
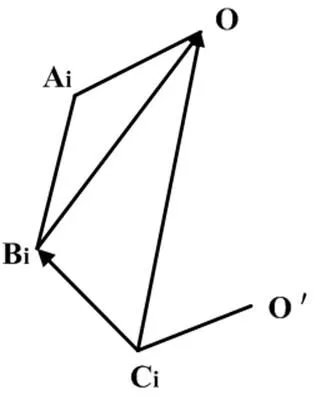
图5 矢量图
如图5,很容易得到矢量关系式CiBi+BiO=CiO,其中BiO和CiO已知,得
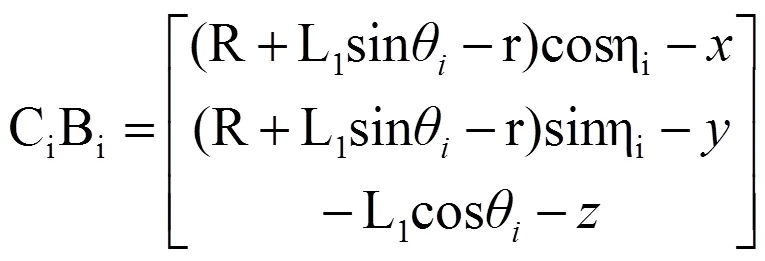
利用|CiBi|=L2, 可得:
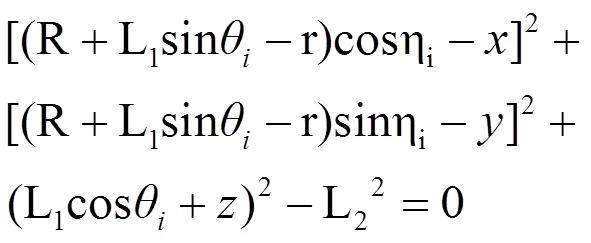
式(1)即为将DELTA机构驱动杆相对静平台张角(输入量)与动平台中心点位置(输出量)相关联的位移方程。
1.2 DELTA机器人逆位移解
运动学逆位移解即已知机构的输出参数,求机构的输入参数;对于DELTA并联机构,即给出结构参数R, r, L1, L2,hi和位置参数x, y, z,求驱动杆相对于静平台的输入角。
在(1)式中,令g=tan(/2),由万能代换得:
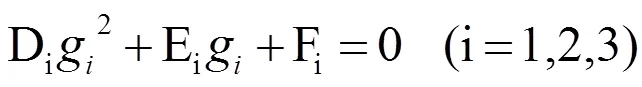
(2)式中,根据三角函数关系,系数Di,Ei,Fi均为由结构参数R, r, L1, L2,hi和位置参数x, y, z构成的已知量,用通式解此一元二次方程,得:
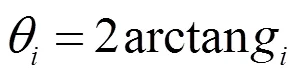
当已知结构参数R, r, L1, L2,hi和位置参数x, y, z时基于式(1)、(2)及(3)利用Matlab编程,不难求出,这里不作赘述。
1.3 DELTA机器人的正位移解
运动学正位移解即已知机构的输入参数,求机构的输出参数。在已知输入参数q1,q2,q3的情况下,可将运动学位移方程(1)整理成非线性方程组:
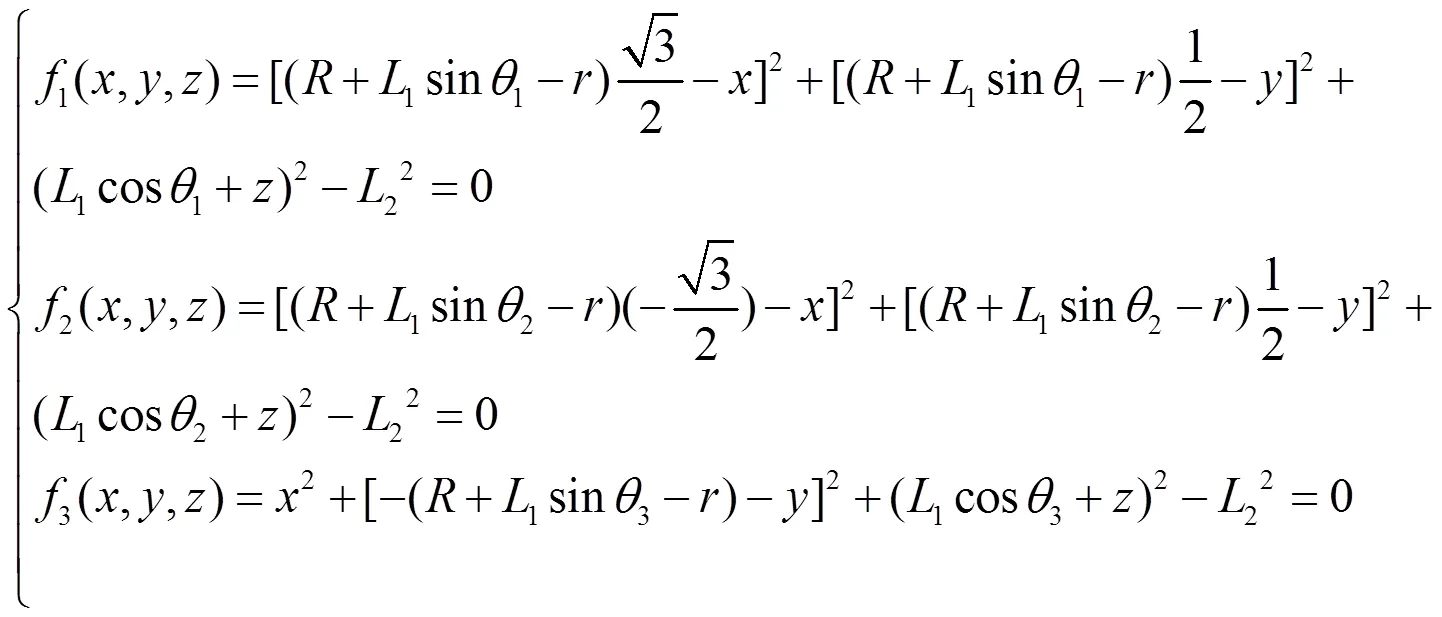
为求解式(4)的非线性方程组,定义目标函数:
(x, y, z)= F(x, y, z)TF(x, y, z) (5)
其中:
F(x, y, z)=[f1(x, y, z) f2(x, y, z) f3(x, y, z)]T(6)
则求非线性方程组(3)解的问题等价于求目标函数(x, y, z)的极小值问题。
2 基于正位移解的工作空间分析方法及其软件实现
机器人的工作空间是指末端执行器上某点(一般取中心点)在空间所能达到的位置的集合,它是衡量机器人工作特性的重要指标之一,使用者要求机器人能夹持工具或工件到达一系列位置,因而研究机器人的工作空间可以判断其是否满足工况要求,完成规定任务。
影响工作空间的因素有很多,例如:(1)杆长的限制:当连杆长度到达运动极限时,工作空间的边界点也就确定了;(2)运动副转角的限制:各运动副受结构尺寸影响,运动角度和范围有限;(3)连杆的干涉:各杆在运动过程中有可能发生干涉,应避免。
确定机器人的工作空间,即在多个变量受限制的情况下,例如机构尺寸受限、运动副运动范围受限等,求解动平台所能到达的位置集合。DELTA型机器人的结构相对简单,其输入参数为驱动杆相对静平台的张角qi(i=1, 2, 3), 同时动平台只作X, Y, Z三个方向的平移,其姿态角不变,因此对于DELTA机器人而言,是分析单一姿态下机构的工作空间。此外,式(1)是基于矢量法的运动学位移方程,式中已经包含了DELTA机器人结构参数、动平台位置参数和驱动杆输入角度之间的关系;只要给定合理的输入角并正确地求解方程,就能得到有效的动平台位置参数,而所有这些可达位置点的集合就是DELTA机器人的工作空间。
综上所述,基于运动学正位移解方程,从输入角度受限这一角度入手,通过代入合理输入角度求解其工作空间;每给定一组输入角度q1,q2,q3可得到一组位置正解,若能给定所有运动副允许范围内的输入角度,得到的正解的集合即为机器人的工作空间。令输入角度的范围为qmin到qmax,为了使qi能取到所有输入角度,采用蒙塔卡洛法,取qi为qmin到qmax之间的随机数,在Matlab中用rand函数实现,生成输入量的随机数:
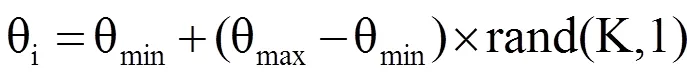
当K足够大,通过(7)式可以使q1,q2,q3取到qmin到qmax范围内的所有值,且此处rand生成的是0~1之间的K个随机数,q1,q2,q3取值时得到的随机数分布是不同的,可以保证q1,q2,q3之间各种角度的排列组合。因此,当K取值较大时,基于正位移解,将输入量qi代入方程组(4),定义,,三个变量,利用Matlab库函数lsqnonlin求解,由于输入量qi有K组,求解的正位移解也有K组,再通过库函数scatter3将K组结果用点集的形式绘制在三维坐标系内,就可以准确地表达DELTA机器人的工作空间。
3 仿真与分析
工作空间仿真算例:
给定一组DELTA型机器人结构参数:静平台R = 200 mm,动平台r = 40 mm,驱动杆L1= 600 mm,从动支链L2= 800 mm;输入量qi的范围定为0°~150°,变量取2000组采样点;运用Matlab编程,生成可视化的工作空间仿真图形:
通过生成的仿真图形可以看到,工作空间以z=0为界,分成上下两部分;由给定的DELTA机器人结构分析可知,当输入角q1,q2,q3同时大于90°时,工作空间中会出现z>0的点,因此实际工作中qi不能同时超过90°;此外,工作空间中z³0的点由于DELTA的装配模式决定是不可达的。
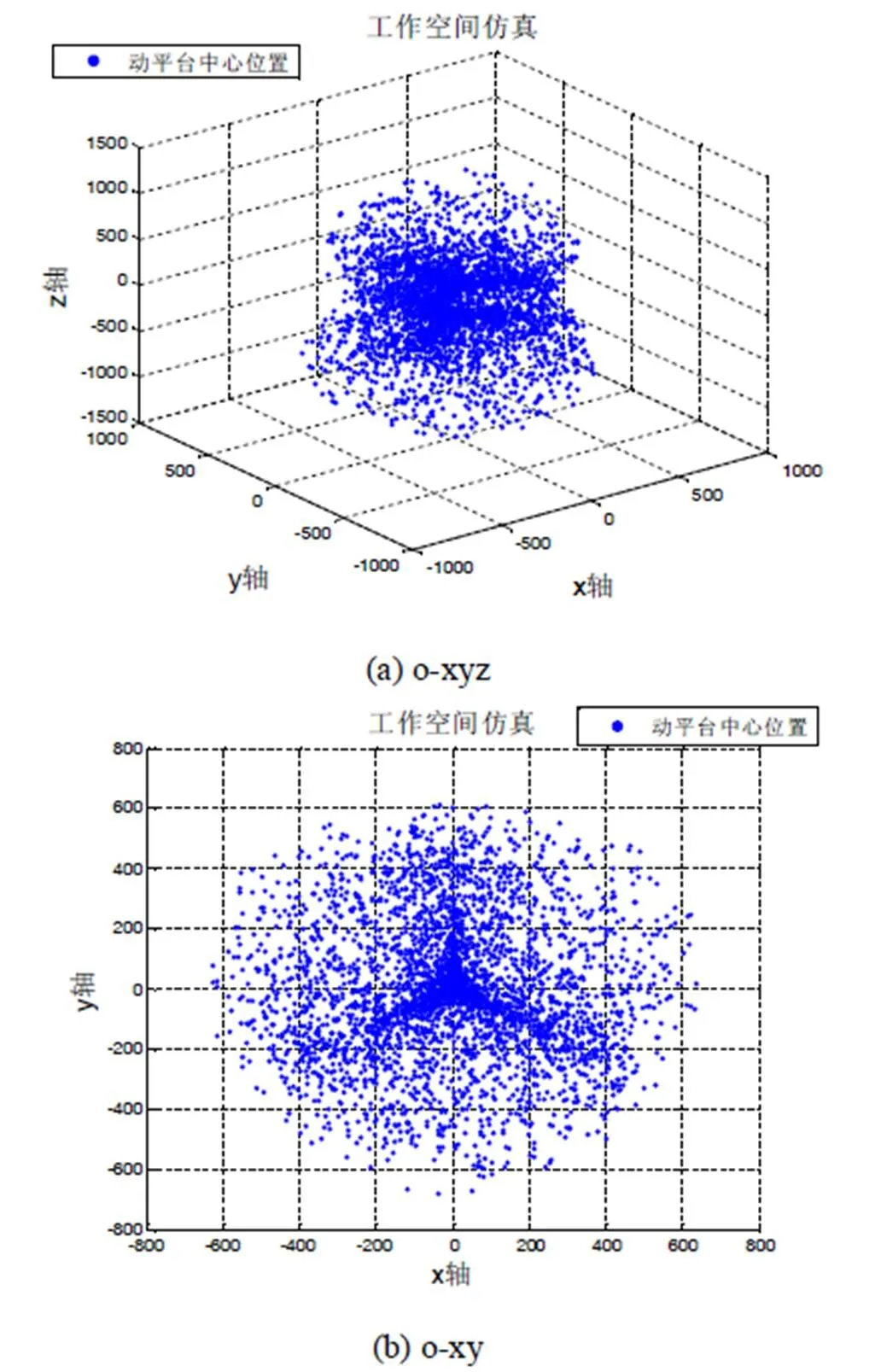
综上所述,在给定的结构参数和输入角度范围下,DELTA机器人的工作空间分布在静平台以下,呈现半球型分布,且随着输入量采样点的增加,半球呈现实体化;本文同时给出了求解DELTA机器人的正解和逆解方法,工作空间是基于正解得到的,若在工作空间中任取一点代入逆解计算公式中,求出的相应输入角都在给定的输入角范围内,则说明基于正解的工作空间分析方法是有效的。
现从工作空间中任取两点为例,(x1, y1, z1)T= (200, 200, -400)T和(x2, y2, z2)T= (-300, -300, -750)T分别代入逆解公式计算,得到结果分别为q1=2.052rad,q2=1.026rad,q3=0.761rad和q1=0.342rad ,q2=0.979rad,q3=1.313rad,换算为角度值后均在0°~150°范围内,验证了基于正解的工作空间分析方法的合理性,说明DELTA机器人在其结构尺寸内,具有较大的工作空间,能够完成生产装配线上的多种分拣、搬运等任务,是一种实用的工业机器人。
4 结论
(1)基于空间机构学理论,建立了DELTA并联机构空间位移模型;
(2)在DELTA并联机构正位移解求取时,将非线性方程组求解问题化归为最小平方和问题,使用数值方法在Matlab软件中编程求解,得到了符合工程实际的位置解。
(3)通过逆解验证了基于正解的工作空间分析方法的有效性、合理性。
[1] 赵杰.朱延河.蔡鹤皋. Delta型并联机器人运动学正解几何解法[J]. 哈尔滨工业大学学报,2003, 35(1): 25-27.
[2] 马晓丽.陈艾华.张雪莲.等. 并联机器人机构的创新与应用研究进展[J]. 机床与液压,2007, 35(2): 235-243.
[3] Szep C , Stan S D, Csibi V . Design, workspace analysis and inverse kinematics problem of Delta parallel robot [J]. MECHANIKA, 2011,17(3): 296-299.
[4] 毕树生.宗光华. Delta 并联微操作手运动学的矢量法分析[J]. 北京航空航天大学学报,2003, 29(4): 339-341.
[5] 黄真.赵永生.赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006.
[6] 刘正君. MATLAB科学计算与可视化仿真宝典[M]. 北京: 电子工业出版社,2009.
Workspace Analysis of DELTA Robot Based on Forward Solution
PENG Yu, *GAO Hong, CHEN Xiao, JIANG Xuan, HU Ru Fang
(Anhui Polytechnic University, Anhui Key Laboratory of Advanced Numerical Control & Servo Technology, Wuhu, Anhui 241000, China)
A parallel mechanism displacement model based on the space agency theory and vector method was built up for the DELTA parallel robot. The numerical solution method of its forward and inverse solutions was investigated and provided the workspace analysis method based on the forward solution. The workspace was simulated by the MATLAB program. The research provides a foundation of trajectory planning of the DELTA robot.
DELTA robot; displacement model; forward solution; inverse solution; workspace
1674-8085(2013)05-0060-05
TP242
A
10.3969/j.issn.1674-8085.2013.05.014
2013-01-24;
2013-04-16
安徽省自然科学基金项目(090414172)
彭 煜(1989-),男,安徽合肥人,硕士生,主要从事数字化设计与制造研究(E-mail:398818321@qq.com);
*高 洪(1963-),男,安徽枞阳人,教授,博士,硕导,主要从事现代设计理论与CAD等研究(E-mail:gaohong0706@sina.com);
陈 啸(1986-),男,安徽安庆人,硕士生,主要从事汽车数字设计与制造研究(E-mail:stevenchan219@foxmail.com);
蒋 璇(1986-),女,安徽马鞍山人,硕士生,主要从事数字化设计与制造研究(E-mail:491054460@qq.com);
胡如方(1986-),女,山东菏泽人,硕士生,主要从事数字化设计与制造研究(E-mail:1415602593@qq.com).
