泊松型元件成败型开关并串联系统可靠度的Fiducial置信限

钟景明，郑海鹰

（温州大学数学与信息科学学院，浙江温州 325035）

泊松型元件成败型开关并串联系统可靠度的Fiducial置信限

钟景明，郑海鹰†

（温州大学数学与信息科学学院，浙江温州 325035）

依据Fiducial理论，给出了泊松型元件成败型开关并串联系统可靠度的Fiducial置信下限的可靠性表达式，并基于元件的定数截尾寿命试验数据和开关的成败型试验数据，利用Beta分布和Monte-Carlo随机模拟的数值计算方法来拟合数据，结果表明，基于Fiducial理论与Beta拟合方法研究该系统置信下限是切实可行的．

并串联系统；可靠度；Fiducial置信限

根据元件的试验数据来研究系统可靠性置信限的方法一般有3种：经典方法、Bayes方法和Fiducial方法[1]．早在1957年，Buehler就提出了求成败型串联系统可靠性置信下限的经典精确解的方法[2]，但由于精确解在计算上困难重重，所以之后统计学学者相继提出了很多求近似解的方法，取得了一系列相当有意义的研究成果，例如，吴和成在《系统可靠性评定方法研究》①中，对寿命元件服从连续型分布的串联或并联系统可靠性的Fiducial近似置信限进行了研究；文献[3]给出了成败型并联系统可靠性置信下限的4种近似解法：LR法、AW I法、ML法和AO法，并进行了大量模拟计算，认为LR法和AO法相对令人满意；文献[4-5]利用将数据折合的方式与Fiducial方法研究了成败型元件的系统可靠性置信下限的近似解．本文将依据Fiducial理论，基于元件和开关的定数截尾寿命试验数据，利用Beta分布和Monte-Carlo随机模拟的数值计算方法来拟合泊松型元件成败型开关并串联系统可靠度的Fiducial置信限．

1 系统的可靠性

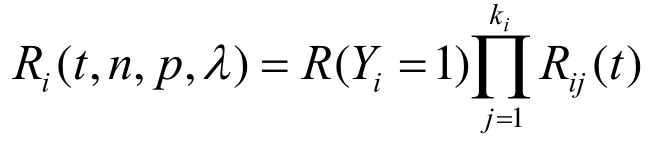
2 λ与p均已知时，系统可靠性精确Fiducial置信限

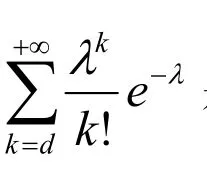
引理2[6]g（x）是x的单调递增（递减）函数，m∈N，则[g（x）]m也是单调递增（递减）函数．

证毕．

设随机变量X服从参数为λ的泊松分布，X1,X2,…,Xn是来自X的一个样本，则2nλ的Fiducial分布为：

其中T=X（1）+X（2）+…+X（r）+（n-r）X（r）．则对置信度为1-α，λ的Fiducial置信下限就为：

定理3 当p为已知时，由于R（t,n,p,λ）是关于λ的严格单调递增函数，故对于置信度为1-α，该系统可靠度R（t,n,p,λ）的Fiducial置信下限就是：

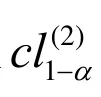
证明：对于固定的λ＞0，由定理2可知，R（t,n,p,λ）是关于p的严格单调递增函数，且开关可靠度p~Beta（S,N-S+1），故有：

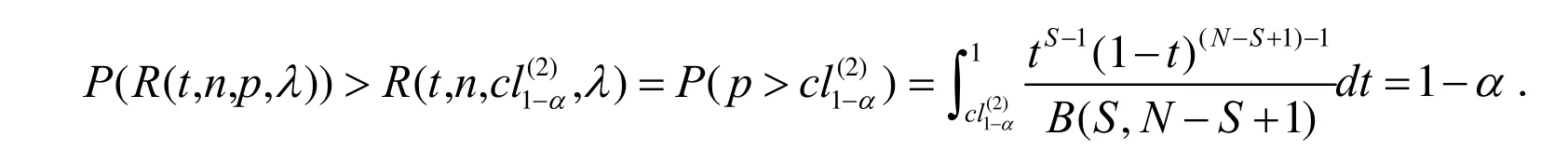
证毕．

3 λ与p均未知时，系统可靠性近似Fiducial置信限

当λ与p均未知时，如果要利用λ与p的Fiducial分布来求R（t,n,p,λ）的精确Fiducial分布显然是比较困难的，所以应考虑其近似分布．由于R（t,n,p,λ）的取值是在[0,1]区间上，而在该区间上取值的Beta分布是一种常见的分布，因而依据一阶矩、二阶矩拟合的原则，系统可靠度R（t,n,p,λ）的Fiducial分布就可以近似地认为是Beta分布．

由（2）式及p~Beta（S,N-S+1）易得：

又有：

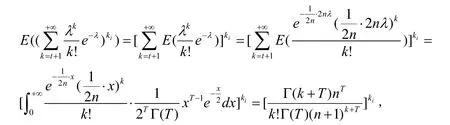
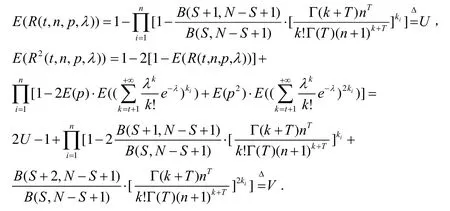
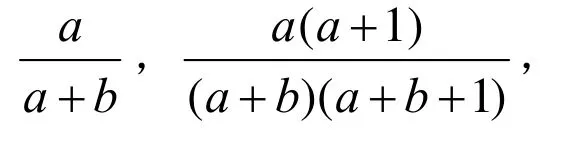
解得：

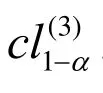
4 模拟分析

为了考究文中Beta拟合方法得到的R（t,n,p,λ）的近似置信下限的精确度，对λ、p均未知时，系统可靠度在上述方法下的近似Fiducial置信限进行模拟计算与分析．当λ、p均未知时，需要选取以下3个指标对模拟结果进行优劣评价[7]：

1）覆盖率v，它越接近预定的置信水平，说明该方法越优；

2）置信下限γ分位点，它与系统可靠度真值越接近，说明该方法越优；

3）置信下限的均方误差e，在以覆盖率或分位点指标为优的前提下，它越小越好．

给定子系统的个数n以及每个子系统所包含的元件数k1,k2,k3,…,kn，同时，给定开关的定数截尾寿命试验数据（N,S），利用Monte-Carlo方法与Matlab软件进行随机模拟，模拟结果见表1．

表1 R（t,n,p,λ） 的模拟计算结果

由表1的模拟结果可以看出，对于所给的3个评价指标，3个样本下的分位点γ与真实值R（t,n,p,λ）之间的绝对误差不超过3％，均方误差e也没有超过2％，覆盖率v与预定的置信水平相差值均小于5％．对于置信度为1-α的可靠度置信下限RL，在Pr{R≥RL}≥1-α的前提下，其均值E[RL]越大，则置信度为1-α的可靠度置信下限RL就越好，反之，若Pr{R≥RL}＜1-α，则认为置信度为1-α的可靠度置信下限RL是冒进了．表1关于该系统可靠度的Fiducial置信限估计结果符合评价要求，Beta拟合方法是切实可行的．但是，如果与精确解或其它近似解进行对比分析，仍然需要更严谨、更深入的探讨，以及更丰富的数据支撑．

[1] 曹普华, 程侃. 可靠性数学引论[M]. 北京：高等教育出版社, 2006：7.

[2] Buehler B J. Confidence Intervals for Product of Two Binomial Parameters [J]. Journal of the American Statistical Association, 1957, 52：482-493.

[3] 盛骤. 成败型并联系统可靠性置信下限的近似解[J]. 高校应用数学学报, 1988, 3（4）；557-562.

[4] 范大茵. 具有多层试验数据的成败型元件之串并联系统及并串联系统可靠性置信下限的近似解[J]. 宇航学报, 1990, （2）：21-27.

[5] 郑海鹰, 范大茵. 成败型元件可靠性估计及近似置信限[J]. 经济数学, 2000, 17（3）：41-44.

[6] 陈威玲, 郑海鹰. Poisson型元件串并联系统和并串联系统的可靠性置信下限[J]. 温州大学学报：自然科学版, 2009, 30（4）：49-54.

[7] 张民悦, 代文华, 姚滔. 开关指数型二部件温贮备系统可靠度Fiducial置信限[J]. 兰州理工大学学报, 2010,36（1）：132-136.

The Fiducial Confidence Lim it of the Reliability for Parallel-series System in Poisson Components and Pass-fail Sw itches

ZHONG Jingm ing，ZHENG Haiying
（College of Mathematics and Information Science,Wenzhou University,Wenzhou,China 325035）

According to Fiducial theory, the paper puts forward reliable expressions of the lower confidence lim it in the parallel-series system of Poisson components and pass-fail sw itches. And based on fixed number testing data of components and pass-fail testing data of sw itches, the fitting data were obtained by means of Beta distribution and Monte-Carlo’s random calculation, confirm ing that the combination of Fiducial theory and Beta fitting method is feasible and practical.

Parallel-series System；Reliability；Fiducial Confidence Limit

O213

A

1674-3563（2013）01-0018-06

10.3875/j.issn.1674-3563.2013.01.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2012-07-02

钟景明（1986- ），男，广东化州人，硕士研究生，研究方向：应用统计．† 通讯作者，wzzhying@163.com① 吴和成. 系统可靠性评定方法研究[M]. 北京：科学出版社, 2006.