基于最大熵方法月球表面亮温度数据处理模拟*

邢树果，苏 彦，周建锋，刘建忠

（1.中国科学院国家天文台，北京 100012；2.中国科学院大学，北京 100049； 3.清华大学工程物理系天体物理中心，北京 100084）

基于最大熵方法月球表面亮温度数据处理模拟*

邢树果1，2，苏 彦1，周建锋3，刘建忠1

（1.中国科学院国家天文台，北京 100012；2.中国科学院大学，北京 100049； 3.清华大学工程物理系天体物理中心，北京 100084）

由天线成像原理可知，通过密云50m天线、“嫦娥一号”卫星（CE-1）和“嫦娥二号”卫星（CE-2）所搭载微波探测仪获取的月球亮温度图是微波天线方向图与真实亮温度图的卷积，所以想清晰准确地还原亮温度图，就必须采取反卷积方法。在处理过程中引入最大熵方法，选择基于Bonavito提出的直接迭代法求解方式，并论证了其作为反卷积方法的可行性，通过一系列的模拟仿真验证其反卷积的有效性。仿真结果理想，对后期处理真实数据（密云50m天线观测数据，微波探测仪观测数据）打下坚实的基础。

射电天文学；最大熵方法；反卷积；亮温度

1 概述

月球是距离地球最近的天体，月球本身不发光，但是会反射太阳光。在红外和微波波段，月球遵循热辐射机制辐射能量，这和月球表层与次表层结构和特性相关。亮温度是天体辐射强度的一种表达方式，等效为同一波长下相同辐射度黑体的温度。要开发月球必须对月球进行全面的探测，了解月球资源，并逐步对资源进行开发。研究月壤特性，在微波频段研究亮温度是必不可少的。另外密云50m天线的卫星通信目前使用的频段是S波段和X波段，当地面接收天线指向探月卫星接收探测和测控数据的时候，就必然要引入月球射电辐射的影响，因此必须要考虑月球射电辐射对天线的接收数据的影响，即对接收系统噪声温度的增加。因此亮温的研究具有重要的意义。

月球的微波观测主要可以分为地基望远镜观测和嫦娥系列卫星探测。密云50m口径的射电望远镜，是目前国内自主设计和建造的口径最大、功能最强的主焦、轮轨式天线。密云50m天线不仅完成了探月工程一期赋予的任务，而且还在探月二期任务中继续承担科学数据接收和卫星精密测定轨的工作，并将在我国空间碎片监测、射电天文观测与研究等领域发挥重要作用。微波波段对亮温的观测，可以实现在X频段（8.4GHz）和S频段（2.3GHz）对月观测，X频段角分辨率达到3'，S频段角分辨率达到11'。由密云50m天线观测得到的月球亮温度图是月球真实亮温分布图与天线方向图的卷积。

微波探测仪（CELMS）是“嫦娥一号”卫星（CE-1）和“嫦娥二号”卫星（CE-2）的有效载荷之一，在执行任务期间，多次覆盖月球表面，获取了大量的微波数据，从而开辟了即“红外月球（Infrared Moon）”和“可见光月球（Visible Moon）”后，又一新的概念“微波月亮”（The Microwave Moon，简称MicM）［1］。CE-1和CE-2搭载的微波探测仪是一个4频段微波辐射计，工作频率分别为3.0、7.8、19.35和37.0GHz。CE-1的绕月飞行高度为200 Km，CE-2的绕月飞行高度为100 Km。

天线观测原理得知，利用微波天线收集辐射时，由天线获取的亮温为天线的亮温值，即天线方向图与月表亮温值的加权。实际上，期望得到的是月球表面的亮温度，所以一个适合有效的亮温重建算法是迫切需要的。

在射电天文学的图像重建领域，CLEAN算法和最大熵方法（Maximum Entropy Method，MEM）一直占据着统治地位。CLEAN算法在处理点源时，效果理想；最大熵方法在处理面源时，会更具有优势［2］。

19世纪中叶，克劳修斯首先把熵引进热力学，d S=d Q/T，其中T表示物质的热力学温度，d Q表示熵增加过程中加入物质的热量。从微观上说，熵是组成系统的大量微观粒子无序度的量度，系统越无序、越混乱，熵就越大。热力学过程不可逆性的微观本质和统计意义就是系统从有序趋于无序，从概率较小的状态趋于概率较大的状态。

1948年香农在创立信息论时，找到一个唯一的量来度量信源的不确定性，这个量与热力学和统计力学中的熵数学形式和物理意义都相近，所以也称为熵，公式定义为S=-P log P，P表示系统中某个事件发生的概率。信息论中的熵，通常称之为信息熵或香农熵，信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。所以，信息熵也可以说是系统有序化程度的一个度量。

在图像恢复领域中，Frieden于1972年首先引入图像熵的概念，导出了图像熵的表达式为：s= -∑x（i，j）ln x（i，j），其中x（i，j）为图像在像素点（i，j）的灰度值。Frieden图像熵概念的引入，使得在图像处理时，有了新的度量标准。针对最大熵算法的具体应用背景及局限性，Frieden、Gull-Daniell、Skilling-Bryan等学者提出了以各自名字命名的最大熵方法［3-5］。

本文在Frieden最大熵方法的基础上，用Bonavito［6］提出的直接迭代法求解最大熵，并通过模拟仿真，验证了基于Bonavito直接迭代法作为求解反卷积方程的有效性。

2 最大熵方法

2.1 最大熵方法的可行性

利用最大熵方法［7］作为一种有效的反卷积方法处理月球表面的亮温度，同时满足了最大多重性原理、第一原理、熵增加原理。

最大多重性原理是指最可能的状态具有最大多重性，即某个状态的多重性越大，则系统最终处于这种状态的可能性也就越大。在图像复原时，用图像熵最大作为约束条件，有公式的定义形式可以保证图像的正定性，也可以证明最大似然分布与最大熵分布是统一的。

第一原理是指在数据不充分的情况下求解，解必须和已知的数据相吻合，而又必须对未知的部分做最少的假定。而图像复原可以认为是从已知数据中提取信息的过程，这一过程由于已知数据量的不足而变得不可唯一求解。信息可以看成是由两个部分导出，一是已知数据，二是由于数据不完全不得不对未知部分做假定。要求熵最大，意味着要求总信息量最少，即由假设而添加的信息量最少，因此最大熵解是最合适的。

熵增加原理指出，一个孤立系统的熵永远不会减少，即趋于最大。所以，最大熵方法对解所作的选择是“合乎自然”的。

2.2 最大熵方法模型

2.2.1 亮温接收模型

通过天线获取的亮温度图为月球表面目标亮温度图与天线方向图的卷积，模型表示如下：

式中，y（i，j）为实际测量的亮温度为天线的亮温度；x（i，j）表示月球表面目标亮温度；PSF为天线方向图函数，此处忽略噪声。

2.2.2 亮温重建模型

利用最大熵方法重建月球表面真实亮温度的，模型表示如下：

解一个反问题都会遇到解的存在性和唯一性问题，难以精确求解。实际的解决办法是寻求一个在某种特定原则下与原图像尽可能接近的近似解或估计解。此处引入图像熵的概念，最大熵恢复就是对图像复原问题加以最大熵约束的恢复方法，在所有满足条件的图像解中，选取熵最大的那组解作为最优解。

2.3 最大熵求解过程

Frieden提出的最大熵方法给出，利用拉格朗日乘子法可以直接求出（2）式中的x（i，j）的表达式

式中，λ11，…，λij为 i*j个朗格朗日乘子；Z（λ11，…，λij）为 λ11，…，λij的函数，为配分函数。Frieden提出的方法就是把（3）、（4）式代入（2）式中，求解非线性的方程组，从而将x（i，j）的最终值求解出来，但是计算量巨大。

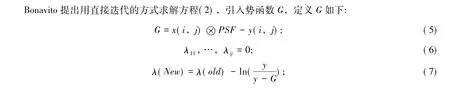
当G为0时，x（i，j）为期望的解，初始时设定λ11，…，λij的初值为0，从而可以确定x（i，j），然后代入（5）式，利用（7）式不停地迭代λ11，…，λij，从而不停地迭代x（i，j），直到最后G的取值为0或接近0，从而确定了x（i，j）为卷积方程的一组解。同时x（i，j）的表达形式保证了每次迭代满足最大熵的约束条件，进而保证了这组解为满足熵最大的条件。

3 模拟仿真计算与结果分析

月球的角径大约有30'，模拟展源1°×1°，经度、纬度各采样100个点，并且结合密云50m的天线方向图，然后将面源与方向图进行卷积，得到实际天线接收的脏图。然后基于Bonavito提出的基于直接迭代法的最大熵方法对脏图进行了洁化，得到洁化后的图像。

图像质量评价［8］从方法上可分为主观评价方法和客观评价方法，前者凭借实验人员的主观感知来评价对象的质量；后者依据模型的量化指标来衡量图像质量。在客观评价方法全参考图像质量评价方法中，均方误差（MSE）和峰值信噪比（PSNR）是最基本和最简单有效的质量评价算法，可以一定程度上反映图像的重建质量，所以此处用均方误差（MSE）和峰值信噪比（PSNR）作为还原后图像质量的评价指标。

其中均方误差定义：

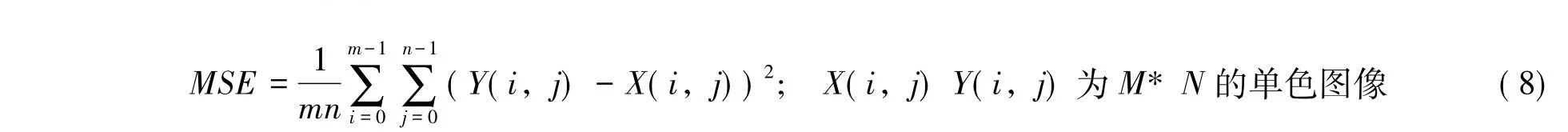
峰值信噪比的定义：

其中天线方向图的模拟计算公式：在50m天线中，D=50m，λ=3.5 cm，工作在X波段；然后在-0.5°到0.5°中采样99个点，以寻求和脏图的数据矩阵一致。

整个仿真是从下面3个方面展开：3.1主要给出了单一天线方向图的最大熵处理效果；3.2是在不断改变天线的方向图参数，从而改变天线的半功率波束宽度，进而探讨最大熵方法的有效性；3.3中撇开规则的亮温分布图，通过随机的亮温分布验证最大熵方法的有效性。

3.1 模拟仿真-1

图1给出了单一天线方向图的仿真流程，其中，（a）为原始数据分布图；（b）为拟合的天线方向图；（c）为得到脏图；（d）为最大熵的处理结果图。表1给出了计算得到的脏图和最大熵处理结果图的均方误差和峰值信噪比。

图1 最大熵处理过程图（a）原始图像；（b）天线方向图/脏束；（c）卷积之后的图像/脏图；（d）最大熵重建后的图像Fig.1 An example of simulated data processed with the MEM（a）True image；（b）dirty beam；（c）blurred image；（d）image resulting from the processing with the MEM

3.2 模拟仿真-2

保持原始数据不变，天线分辨率降低，产生不同的天线方向图，从而得到不同的脏图；最大熵基于不同的方向图进行还原，看得到的洁图随天线方向图的变化关系。

表1图像质量评价指标MSE和PSNRTable 1 Comparison of MSE and PSNR values of the blurred image and MEM result image

图2是天线分辨率（D/λ分布取1 000，800，600，400）的不断改变，从而导致天线方向图的不断变化，随之脏图对应不同天线方向图的响应。图3是利用最大熵方法基于脏图和其对应的天线方向图还原出的洁图。表2是利用MSE和PSNR对最大熵还原后的洁图进行的一个质量评估结果。图4和图5中分别绘制了对应不同波束宽度MSE和PSNR的变化曲线。3.3 模拟仿真-3

图2 不同的天线方向图以及对应的脏图Fig.2 Different antenna patterns and the corresponding dirty images

图3 不同的天线方向图与其对应最大熵重建图Fig.3 Different antenna patterns and corresponding MEM result images

考虑到上面两个模型都是基于简单的有规则的亮温分布，本仿真的构建思路如下：

a、随机生成一个100×100的矩阵拟合亮温度，数值范围在250到280之间，如图6（a）；图4 不同天线方向图下对应的MSE值Fig.4 The MSE values corresponding to

different antenna patterns图5 不同天线方向图对应的PSNR值Fig.5 The PSNR values corresponding to

different antenna patterns

图6 最大熵处理过程图（a）原始图像；（b）天线方向图/脏束；（c）卷积之后的图像/脏图；（d）最大熵重建后的图像Fig.6 An example of simulated complex image processed with the MEM.（a）True image；（b）dirty beam；（c）blurred image；（d）image resulting from processing with the MEM

b、生成一高斯函数拟合天线方向图，矩阵大小为15×15，E面表示如图6（b）；

c、将亮温度图与天线方向图做卷积，结果如图6（c）；

d、对6（c）图进行最大熵还原，结果如图6（d）。3.4 仿真结果分析

表2不同方向图下对应的MSE和PSNRTable 2 The MSE and PSNR values of blurred images and MEM result images corresponding to different antenna patterns

模拟仿真1中，拟合100×100的数据矩阵作为面源，经过天线方向图加权脏化后，明显可以看出与原始面源存在差异。脏图经过最大熵方法重建后，首先从主观上就可以看出重建后的图像较脏图更加接近原始面源；其次从客观角度，MSE由1 503.51下降到4.202 3，PSNR从14.249 5提升到了39.785 8。

模拟仿真2中，保持原始不变，随着天线方向图分辨率的降低，对原始数据观测得到脏图的质量明显下降，MSE呈现增大趋势，从1 503.51增大到2 299.71；PSNR不断降低，由14.249 5减小到12.403 9。脏图经过最大熵重建后，MSE变化范围为4.202 3到14.847 4；PSNR变化范围为39.785 8到14.847 4。

利用最大熵重建后，均方误差降低，峰值信噪比提高，图像质量改善。但是也很容易可以看出随着方向图的变化重建后的洁图的质量会有相应的影响，但相比对应的脏图，图像的质量有了很大提高。

模拟仿真3中，通过不规则的展源分布作为原始数据，对其进行卷积，然后用最大熵进行还原，从结果图中可以直观的看出还原后的图像比脏图更加接近原始图像，进一步验证了最大熵方法作为一个反卷积方法的有效性。

4 结论

本文讨论了最大熵方法作为一个反卷积方法的可行性，并在此基础上进行了一系列的模拟仿真，仿真结果理想，验证了其有效性，为下一步处理密云50m天线观测数据、CE-1和CE-2微波探测仪探测微波数据奠定了良好的基础。目前针对嫦娥系列CELMS探测得到的月球亮温多采用线性的方式［9］，最大熵方法的应用能有效的填补这一空缺，具有较大的实用和推广价值。

［1］Jiang J S，Wang Z Z.The microwave moon-microwave sounding the lunar surface from China lunar orbiter CE-1 satellite［R］.37th COSPAR meeting，Montreal，Canada，June 2008.

［2］Srarck JL，Pantin E，Murtagh F.Deconvolution in astronomy：a review［J］.The Publications of the Astronomical Society of the Pacific，2002，114（800）：1051-1069.

［3］Frieden B R.Restoring with maximum likelihood and maximum entropy［J］.Journal of the Optical Society of America，1972，62（4）：511-518.

［4］Gull SF，Daniell JG.Image reconstruction from incomplete and noisy data［J］.Nature，1978，272：686-690.

［5］Skiling J，Bryan R K.Maximum entropy image reconstruction：general algorithm［J］.Monthly Notices of the Royal Astronomical Society，1984，211：111-124.

［6］Bonavito N L，Dorband JE，Busse T.Maximum entropy restoration of blurred and oversaturated Hubble Space Telescope imagery［J］.Applied Optics，1993，32（29）：5768-5774.

［7］吴乃龙，袁素云.最大熵方法［M］.湖南：湖南科学技术出版社，1991：12.

［8］蒋刚毅，黄大江，王旭，等.图像质量评价方法研究进展［J］.电子与信息学报，2010，32（1）：219-226.Jiang Gangyi，Huang Dajiang，Wang Xu，et al.Overview on Image Quality Assessment Methods［J］.Journal of Electronics＆Information Technology，2010，32（1）：219-226.

［9］王振占，李芸，张晓辉，等.“嫦娥一号”卫星微波探测仪数据处理模型和月表微波亮温反演方法［J］.中国科学（D辑：地球科学），2009，139（8）：1029-1044.Wang Zhenzhan，Li Yun，Zhang Xiaohui，et al.In-orbit calibration and antenna pattern correction to CE-1 lunar microwave sounder（CELMS）［J］.China Science（Series D：Earth Sciences），2009，139（8）：1029-1044.

Simulations of Processing of Data of Brightness Tem perature M ap of the Lunar Surface w ith the M aximum Entropy M ethod

Xing Shuguo1，2，Su Yan1，Zhou Jianfeng3，Liu Jianzhong1
（1.National Astronomical Observatories，Chinese Academy of Sciences，Beijing 100012，China，Email：xingsg@nao.cas.cn； 2.University of Chinese Academy of Sciences，Beijing 100049，China；3.Tsinghua Center for Astrophysics，Department of Engineering Physics，Tsinghua University，Beijing 100084，China）

As understandable from the data acquisition processes a brightness temperature map of the lunar surface recorded by the microwave detector on the Miyun 50m radio telescope，CE-1，or CE-2 is the convolution of the actual brightness temperature distribution by the antenna pattern.If we want to accurately restore the brightness temperature distribution a deconvolution method is needed.Among the deconvolution methods of the radio astronomy，the CLEAN method and the Maximum Entropy Method（MEM）are themost popular.Though the results of the CLEAN method in processing data of point sources are satisfactory，the MEM hasmore advantages in dealing with those of extended sources.This paper chooses the MEM for this reason.The paper first describes the MEM and a direct iterative solution algorithm proposed by Bonavito.The paper shows the feasibility of the Bonavita algorithm and validates it through a series of simulations.The satisfactory simulation results provide the basis for future use of the MEM to deconvolve actual data observed by the Miyun 50m radio telescope，CE-1，and CE-2.Currently，the data processing method for the Chang E Series CELME detection uses the linear method.The application of the MEM can effectively open new opportunities for improving data quality and leading to potential discoveries.

Radio astronomy；Maximum Entropy Method；Deconvolution；Brightness temperature

T161

：A

：1672-7673（2013）03-0255-09

国家自然科学基金（11173038）资助.

2012-09-20；修定日期：2012-10-22

邢树果，男，硕士.研究方向：天文技术与方法.Email：xingsg@nao.cas.cn

CN 53-1189/P ISSN 1672-7673