分布式多入多出正交频分复用系统帧同步的阈值选取准则

姚志强 罗 荆 裴廷睿 周震宇

（1.湘潭大学信息工程学院，湖南 湘潭411105；2.智能计算与信息处理教育部重点实验室，湖南 湘潭411105）

引 言

多入多出（Multiple Input Multiple Output，MIMO）系统和正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术［1-2］的结合能有效地提高系统的容量［3］、频谱利用率和数据传输的可靠性，是下一代无线通信系统（如LTE，802.16m（WiMAX）和802.11n（WLAN））的关键技术.通信系统中，好的定时同步性能是接收机进行后续信号处理的必要条件.而在MIMO-OFDM系统中，定时同步的实现难度加大，尤其是对于分布式系统［4］，发射天线/接收天线在地理位置上呈现分布式摆放，不同发射天线发送的数据帧到达同一接收天线的时间不同，从而产生天线间互时延（Inter Transmitter Delay，ITD），由于各个发射天线无法共用同一个射频本振源，接收天线接收到的各发射天线数据的载频不同，从而产生互频偏（Inter Transmitter Frequency Offset，ITFO），在这种模型下，微小的同步偏差就会导致系统性能大幅度降低.因此，分布式MIMO-OFDM系统定时同步技术成为了新的研究热点之一.

定时帧同步算法［5-8］需要设定一个阈值，当接收信号同步度量值超过这一阈值时判定为正确帧同步.从目前的研究来看，传统正确帧同步的阈值选取的依据是仿真实验或经验值，还没有人给出一个理论的阈值选取准则.本文的目标是根据分布式MIMO-OFDM系统帧同步度量函数的统计特征、正确帧同步概率的理论计算方法和正态分布的3σ原则，提出帧同步算法的阈值选取准则，并根据文中计算得到的阈值指导实际阈值的选取，使系统在不同MIMO发射天线数目和指定信噪比（Signal Noise Ratio，SNR）下选择合适的阈值，其正确帧同步概率理论上总能达到100%.

1 阈值选取准则

1.1 信号模型

Nt×Nr的分布式 MIMO-OFDM系统中，第i根天线发射的信号可以表示为

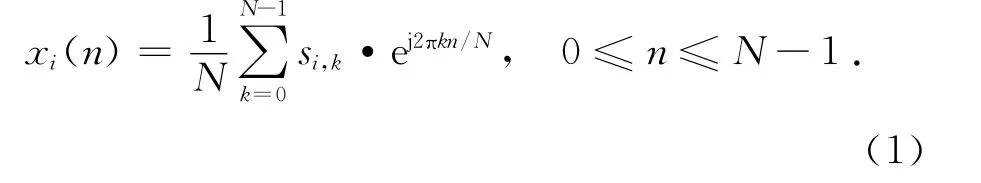
接收端，第j根天线收到的信号可以表示为

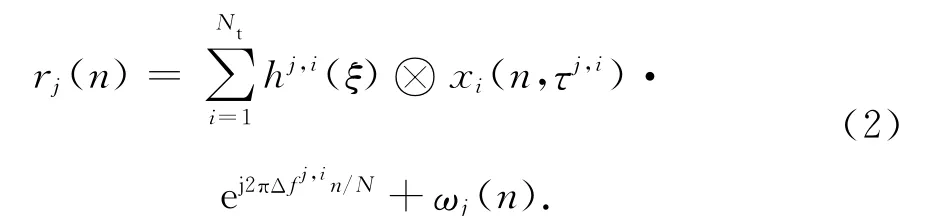
式（1）和（2）中：Nt为发射天线数目；Nr为接收天线数目；N为子载波个数；si，k是第i根天线的第k个子载波上的频域符号；τj，i是第i根发射天线到第j根接收天线的归一化时延，由于移动端接收天线集中摆放，同一发射天线到所有接收天线的时延可认为相同，即τj，i＝τi；Δfj，i是第i根发射天线到第j根接收天线的频偏；ωj（n）是高斯白噪声.

假设训练序列P＝｛p（0）p（1）...p（N-1）｝，为了简化分析，采用MIMO平坦衰落信道并且忽略频偏，则第j根接收天线收到的信号为

训练序列和噪声的实部与虚部均值都为0，方差分别为σ2p＝E［Re｛｝p2］＝E［Im｛｝p2］和σ2ω＝E［Re｛｝ω2］＝E［Im｛｝ω2］，则每根接收天线的信噪比为

在接收端定义的Nt维自相关估计器中，第i维估计器的帧同步度量函数定义为

式中：

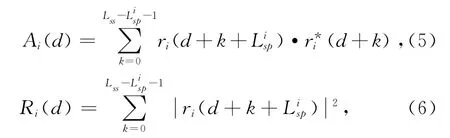
Lss是前导序列长度，Lisp是第i根发射天线的训练序列的周期长度，每根发射天线的Lisp均不同，且Lisp不等于Lskp的倍数，k＝1，…，Nt，k≠i.

求得第i根天线发射信号的帧头捕获位置为

1.2 阈值选取准则

为了得到正确帧同步的阈值选取准则，本文首先分析和提出基于前导的分布式MIMO-OFDM系统的帧同步度量函数的分布函数.

命题1 帧头捕获位置处于前导之中时，可得基于前导的分布式MIMO-OFDM系统的帧同步度量函数服从如下高斯分布为

式中：σ2p表示训练序列的实部和虚部的方差；σ2ω表示噪声的实部和虚部的方差.

证明 由于各信号和噪声矢量在不同的方向上，需将它们正交分解为主信号的同相和正交方向，再计算和分析.捕获点在前导中时，利用正交分解，当采用带有高斯噪声的信号包络时，莱斯分布近似于高斯分布［9］，同相部分远大于正交部分.因此，将包络近似为同相部分，则服从高斯分布且均值为＝2另外Ri（dopt）也服从高斯分布且均值为E（Ri（dopt））＝.定义Qi（dopt）的平方根为的分子和分母都由高斯随机变量构成，因为这些高斯随机变量的标准差都远小于它们的均值，所以Qi（dopt）可近似为一个高斯随机变量［9-10］，且有：

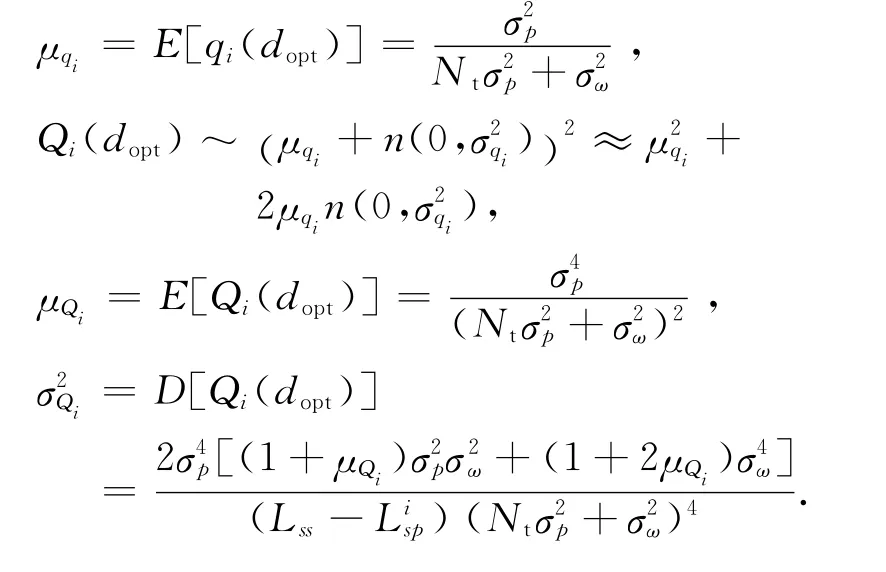
命题2 当捕获的帧头位置处于前导之外时，属于误捕获，其帧同步度量函数服从如下卡方分布：

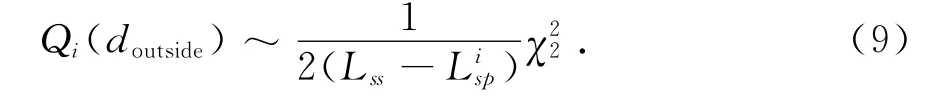
式中χ22是自由度为2的卡方分布.

证明捕获点落在前导外时，样本仅由噪声项组成，方差σ2r＝E［Re｛｝r2］＝E［Im｛｝r2］，则［9］：

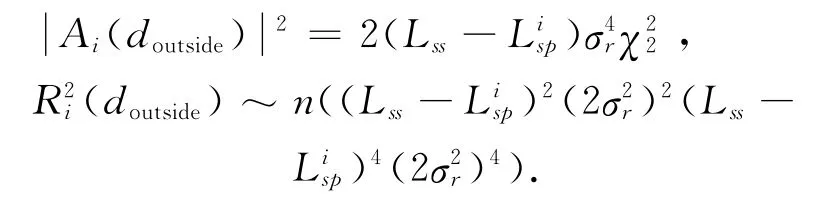
式（9）表明：由于在前导符号外没有训练序列信号，所以其帧同步度量均值和方差与SNR无关，即不管SNR如何变化，帧同步度量的值都会接近零，与落在前导内的值（较大）形成鲜明对比，利用这一特性就可以正确捕获到帧头.

命题3 为了使分布式MIMO-OFDM系统在不同MIMO发射天线数目和指定的SNR下，理论上达到100%的正确帧同步，本文提出根据指定SNR得到的帧同步度量，按照式（10）、（11）计算得到任意正确帧同步性能（包括100%）下的阈值：

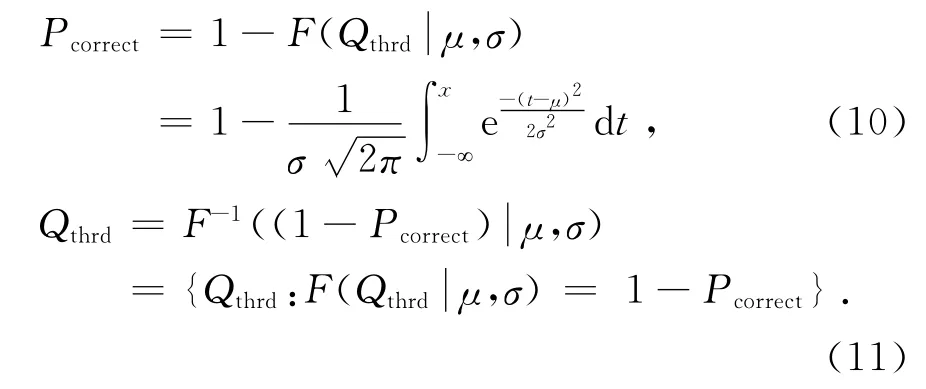
为了简化运算，根据正态分布的3σ原则［8］，提出正确帧同步概率达到99.87%的阈值选取准则：

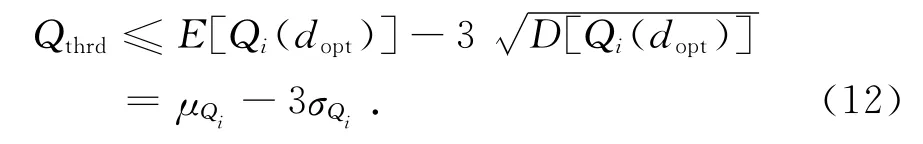
式中：μQi是同步度量函数的理论均值；σQi是理论标准差，由命题1求取.

帧同步算法设定Qi＞Qthrd时捕获到帧头，对帧同步度量函数的概率密度f（Qi）在一定范围内积分，分别定义正确帧同步概率、漏捕获概率和误捕获概率为

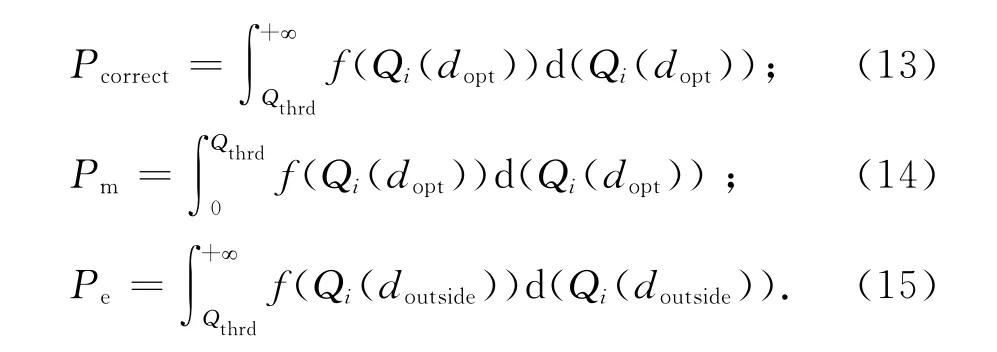
式（14）表示当捕获位置处于前导中，而帧同步度量值小于阈值，此时发生漏捕获.式（15）表示当捕获位置处于前导外，而帧同步度量值超过阈值，此时发生误捕获.

图1显示了系统在不同MIMO发射天线数目和指定SNR下第i根发射天线正确帧同步时的度量值，实线与虚线的距离表示3倍标准差.假设Lss＝256，Lisp＝64.

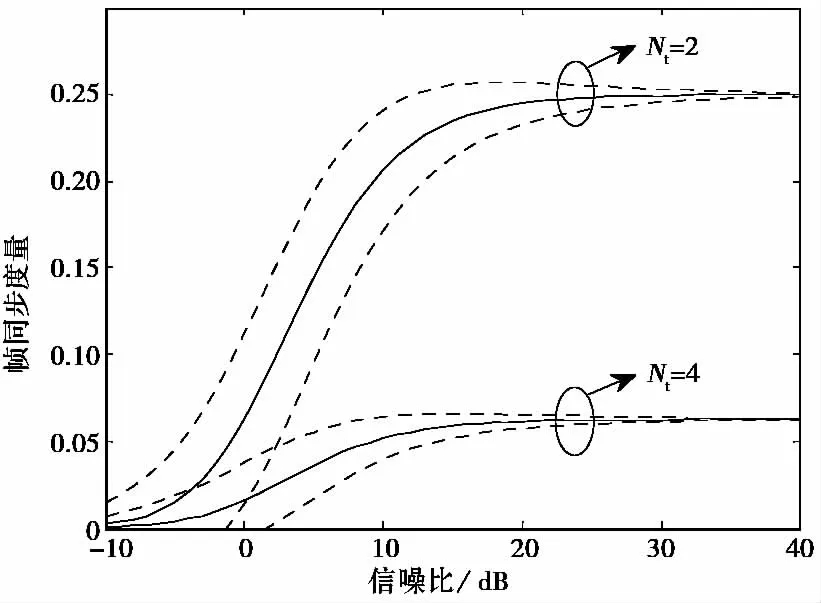
图1 MIMO平坦衰落信道下第i根发射天线正确帧同步时的度量值

如图1所示，当RSN＝3dB时，发射天线数目Nt＝2则μQi-3σQi＝0.059 0，根据式（8）和（12），阈值可以选0.059 0；Nt＝4则μQi-3σQi＝0.006 4，阈值可以选0.006 4.发射天线数增加时，信号能量Ri（d）增大，帧同步度量值减小，选取的阈值减小.

2 实验结果

为了分析系统在不同MIMO发射天线数目和指定SNR下阈值选取准则的有效性，本文对系统在发射天线数为2和4以及SNR为3dB、5dB和10 dB（达到工程实用标准［11］）时的阈值选取准则分别进行了蒙特卡洛仿真，得到了MIMO平坦衰落信道下，帧同步度量函数的概率密度曲线和正确帧同步概率的仿真值，并与理论值进行了对比.为简化分析，仅讨论第1根发射天线，其他天线分析和仿真方法相同.

仿真参数为：前导符号的总长度Lss＝256，发射天线1的训练序列选用长度为L1sp＝64的Zadoff序列p（64）1，发射天线2选用L2sp＝81的Zadoff序列p（81）2，发射天线3选用L3sp＝100的Zadoff序列p（100）3，发射天线4选用L4sp＝121的Zadoff序列p（121）4，一个前导符号包括的训练序列个数为k＝｛4，3，2，2｝，时延τ1＝100个样本，τ2＝150个样本，τ3＝200个样本，τ4＝250个样本，仿真次数10 000次.

2.1 帧同步度量函数的概率密度曲线

图2给出了系统在不同MIMO发射天线数目和指定SNR下第1根发射天线正确帧同步时的帧同步度量函数的概率密度曲线，设帧同步度量函数的理论均值为μQi，理论标准差为σQi；仿真（样本）均值为ˉμQi，仿真（样本）标准差为ˉμQi.

如图2所示，根据式（8）和（12），计算得到系统在不同MIMO发射天线数目和指定SNR下第1根发射天线理论上达到100%同步应选取的阈值，如表1所示.

表1 系统在不同Nt和指定SNR下第1根发射天线理论上达到100%同步应选取的阈值

表1中应选取的阈值（理论计算获得）比实际‘3σ’值（仿真获得）小，满足本文提出的阈值选取准则.如图2所示在这样的阈值选取下：

1）发射天线数目相同时，SNR越大，正确帧同步时的同步度量函数概率密度的理论值和仿真值越接近，即应选取的阈值与实际‘3σ’值越接近.

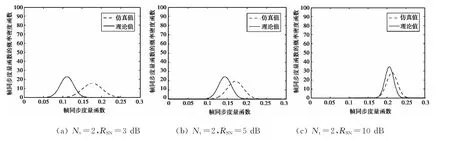
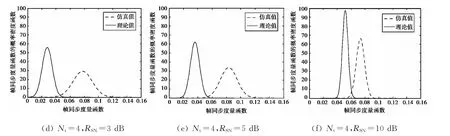
图2 MIMO平坦衰落信道下第1根发射天线正确帧同步时度量值的概率密度曲线

2）SNR相同时，根据式（8），发射天线数目越多，方差越小，则图中曲线越尖锐，性能越好.

2.2 阈值选取准则的准确性和有效性验证

评价阈值选取准则的指标主要有正确帧同步概率（式（13））、漏捕获概率（式（14））和误捕获概率（式（15））.

1）正确帧同步性能

由式（10）、（11）可知，根据本文提出的阈值选取准则，实际仿真时选取理论计算得到的阈值，可以使系统在不同MIMO发射天线数目和指定的SNR下达到任意的正确帧同步概率.图3给出了按照表1选取阈值的理论和仿真结果，显示不论是理论值还是仿真值，在大于指定SNR后均可达到100%的正确帧同步.

误差分析：文中选取的阈值和实际‘3σ’值产生偏差的原因主要是仿真的次数以及性能模型在推导过程中的数学近似.同步度量值的均值和方差都与提出的性能模型理论值接近，但是仿真得到的值略大于理论计算值，其原因是信号项r＊d＋m和rd＋m＋L在模型中假设是相互独立的.当发射天线数目相同时，SNR越大，正确帧同步时的同步度量函数的均值和方差与理论值越接近，则选取的阈值与实际‘3σ’值越接近.SNR达到和超过选取阈值的指定SNR值时，正确帧同步概率均达到100%.

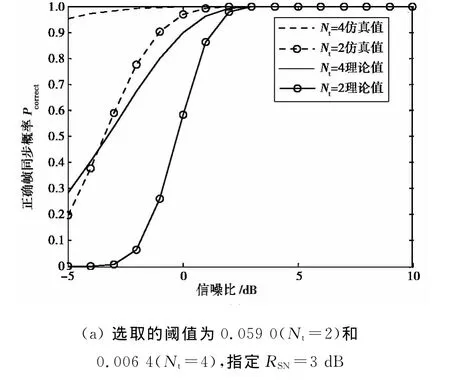
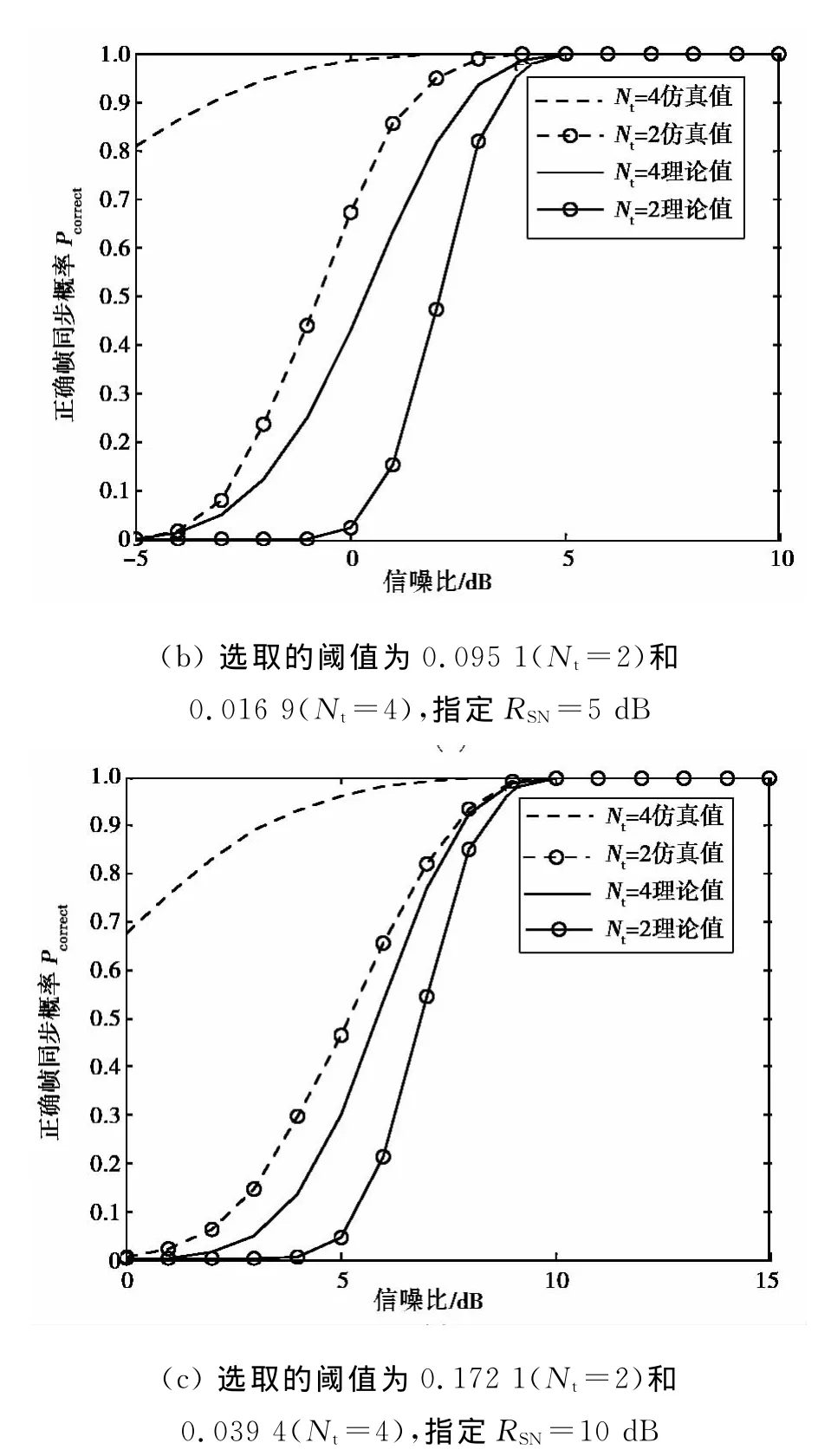
图3 MIMO平坦衰落信道下不同发射天线数目和指定RSN下的正确帧同步概率

2）误捕获性能

由前面的分析可知，阈值选取的准确性对误捕获性能的影响很小.但是，因为帧同步度量函数的值与发射天线数目以及SNR有关，当SNR较低或者天线数目较大时，帧同步度量函数的值较小，这时选取上述理论计算的阈值可能造成一定的误捕获.

图4给出了MIMO平坦衰落信道下，无有效信号、噪声功率为0dBW时得到的噪声同步度量函数曲线.

如图4所示，如果选取的阈值为0.03，将有两次误捕获的可能，误捕获概率为2%.

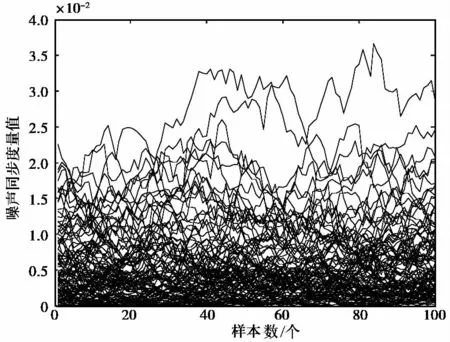
图4 MIMO平坦衰落信道下噪声同步度量函数曲线

根据式（9），加窗长度Lss-Lisp不同，噪声同步度量值Qi（doutside）不同.图5给出了 MIMO平坦衰落信道下4根不同天线的噪声同步度量值的均值和方差，同一天线在不同噪声功率时的噪声同步度量值可以认为是基本相同的，不同天线的Lss-Lisp越大，Qi（doutside）的均值和方差越小.

因为P（X＞χ20.005（2））＝0.005，查表［10］可得χ20.005（2）＝10.597，选取第1根天线Ls1p＝64，根据式（9）和（11），误捕获概率约等于零（0.5%）的阈值为，即应选取阈值大于或等于0.027 6.

通过分析对比可知：

1）2根发射天线在信噪比为3dB、5dB和10 dB时选取的阈值都小于实际‘3σ’值并大于0.0276，对误捕获性能没有影响，误捕获概率约等于零，达到工程实用标准［11］.

2）4根发射天线虽然在指定信噪比时选取的阈值都小于实际‘3σ’值，但在3dB和5dB时选取的阈值小于0.027 6，这时会有一定的误捕获，必须对满足正确帧同步概率为100%和误捕获概率约等于零的阈值进行匹配，相应地调整阈值.如3dB时实际‘3σ’值为0.036 5，大于0.027 6，可以选取0.027 6作为阈值；5dB时实际‘3σ’值为0.048 0，大于0.027 6，可以选取0.027 6作为阈值.

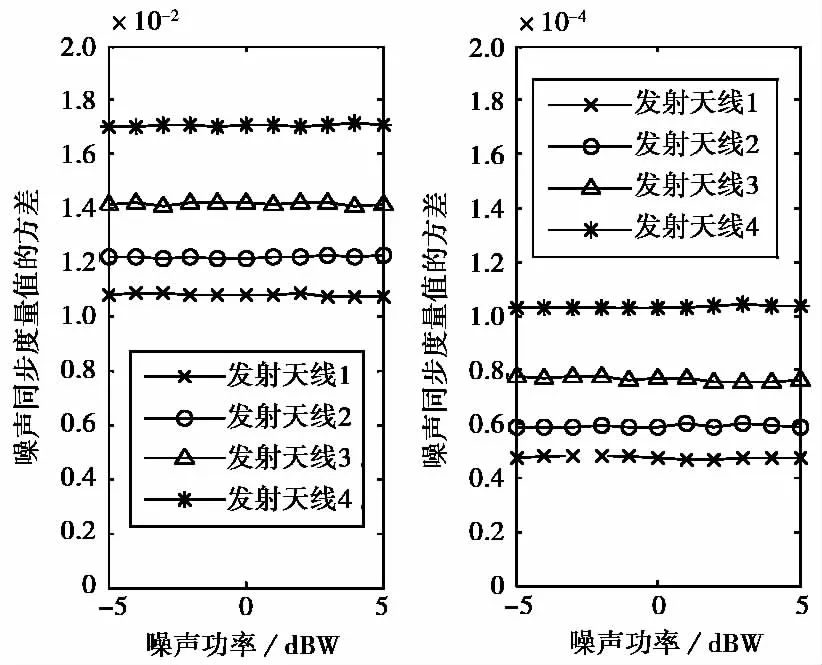
图5 MIMO平坦衰落信道下噪声同步度量值的均值和方差

图6中选取的阈值小于实际‘3σ’值（正确帧同步概率达到100%）并且大于或等于0.027 6（误捕获概率约等于零），即同时满足正确帧同步概率和误捕获概率的要求.

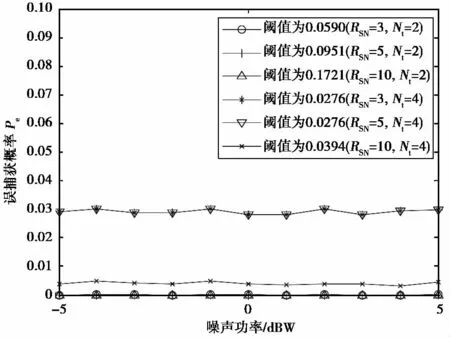
图6 MIMO平坦衰落信道下不同阈值的误捕获概率

由图6可知：将阈值进行匹配调整后，2根发射天线在信噪比为3dB、5dB和10dB时的误捕获概率几乎为零，4根发射天线在信噪比为10dB的误捕获概率约等于零（小于0.5%）.4根发射天线在信噪比为3dB和5dB时的误捕获概率接近3%.其主要原因是发射天线数增加时，没有对帧同步度量函数进行相应的修改，因此导致信号能量Ri（d）增大，帧同步度量值减小，选取的阈值减小，使得选取的阈值接近误捕获界线.

3）漏捕获性能

漏捕获主要出现在低SNR的情况，而由表1可知选取的阈值在低SNR时远低于实际‘3σ’阈值.因此，漏捕获的概率极低，在本文的仿真参数下，没有出现一次漏捕获的现象.

3 结 论

本文根据分布式MIMO-OFDM系统中帧同步度量函数的统计特征和正确帧同步概率的理论计算方法，提出了正确帧同步的阈值选取准则.同时根据正态分布的3σ原则，又给出了简化了的选取准则，即3σQi，可达到99.87%的正确帧同步概率.

通过对帧同步度量函数的概率密度曲线和正确帧同步概率的理论值与仿真值进行对比分析，验证了系统在不同MIMO发射天线数目和指定SNR下阈值选取准则的正确性和有效性：1）发射天线数目相同时，SNR越大，正确帧同步时的同步度量函数的概率密度曲线的理论值和仿真值越接近，即应选取的阈值与实际‘3σ’值越接近.2）SNR相同时，发射天线数目越多，方差越小，性能越好.采用本文提出的阈值选取准则，SNR达到和超过选取阈值设定的SNR值时，正确帧同步概率理论上均达到100%；低于选取阈值设定的SNR值时，虽然理论上天线数目越多性能越好，但是在实际中如果天线数目增加，会大幅度增加前导设计以及接收机处理的算法复杂度.

实验发现发射天线数增加时，信号能量Ri（d）增大，帧同步度量值减小，选取的阈值减小，将导致选取的阈值接近误捕获界线，但是此时误捕获概率仍然很小，可以达到工程实用标准［9］.根据这种现象，将来在设计算法时，应该对帧同步度量函数进行相应的改进，减少误捕获，即可提高同步的性能.

［1］SCHMIDL T M，COX D C.Robust frequency and timing synchronization for OFDM［J］.IEEE Transactions on Communications，1997，45（12）：1613-1621.

［2］AWOSEYILA A B，KASPARIS C，EVANS B G.Robust time-domain timing and frequency synchronization for OFDM systems［J］.IEEE Transactions on Consumer Electronics，2009，55（2）：391-399.

［3］肖海林，聂在平，杨仕文.室内 MIMO无线信道：模型和性能预测［J］.电波科学学报，2007，22（3）：385-389.XIAO Hailin，NIE Zaiping，YANG Shiwen.Indoor MIMO wireless channels：models and performance prediction［J］.Chinese Journal of Radio Science，2007，22（3）：385-389.（in Chinese）

［4］CASTANHEIRA D，GAMEIRO A.Distributed antenna system capacity scaling［Coordinated and Distributed MIMO］［J］.IEEE Wireless Communication Magazine，2010，17（3）：68-75.

［5］ZHOU En，ZHANG Xing，ZHAO Hui，et al.Synchronization algorithms for MIMO OFDM systems［C］//Wireless Communications and Networking Conference.New Orleans：IEEE，2005：18-22.

［6］吴 赟，罗汉文，宋文涛.瑞利衰落信道下改进的OFDM符号定时算法［J］.电波科学学报，2006，21（6）：825-829.WU Yun，LUO Hanwen，SONG Wentao.An improved symbol timing recovery algorithm for OFDM systems in rayleigh fading channels［J］.Chinese Journal of Radio Science，2006，21（6）：825-829.（in Chinese）

［7］GUO Feng，LI Dong，YANG Hongwei.A novel timing synchronization method for distributed MIMOOFDM system［C］//IEEE Vehicular Technology Conference.Melbourne，2006，4：1933-1936.

［8］姚志强，盛孟刚，尹俊勋.MIMO-OFDM分布式天线系统的定时同步算法［J］.电波科学学报，2010，25（4）：717-724.YAO Zhiqiang，SHENG Menggang，YIN Junxun.Timing synchronization algorithm for MIMO-OFDM systems with distributed antennas［J］.Chinese Journal of Radio Science，2010.8，25（4）：717-724.（in Chinese）

［9］SIMON M K.Probability Distributions Involving Gaussian Random Variables-A Handbook for Engineers，Scientists and Mathematicians［M］.New York：Springer，2006.

［10］陈 萍，李 文，张正军.概率与统计［M］.北京：科学出版社，2006.

［11］IEEE Std 802.16e-2005IEEE Standard for Local and Metropolitan Area Networks-Part 16：Air Interface for Fixed and Mobile Broadband Wireless Access Systems-Amendment 2：Physical and Medium Access Control Layers for Combined Fixed and Mobile Operation in Licensed Bands and Corrigendum 1［S］.New York：IEEE，2006：352.