空间光学遥感器运动学支撑方案设计与分析*
2013-03-11李炳强
李炳强,何 欣,袁 涛
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院 研究生院,北京 100039)
引 言
空间光学遥感器的支撑结构将遥感器安装在飞行器的机体上,是连接遥感器与飞行器的机械部件,也是影响成像质量的重要因素。为满足光学系统的成像要求,其设计应实现遥感器自由度全约束,保证光轴指向,同时需要隔离或降低机体平台精度对遥感器性能的影响。在飞行器的发射和在轨运行中,机体平台会产生相对位移,如果采用刚性支撑结构的安装形式,相对位移会引发遥感器较大的结构内应力而导致其形变,降低成像质量。鉴于上述条件,支撑结构应尽量降低由机体平台相对位移施加于遥感器的应力值和应变值。所以,空间光学遥感器的支撑结构设计广泛地采用运动学支撑方案[1-4]。
在运动学定位支撑结构的设计中,过约束容易引起残余应力、发生形变、降低成像质量,对构件加工的精度和成本提出了更高要求。通过合理的设计,可以减少甚至消除过约束,降低由于加工和装配误差引起的内应力[5-6]。
为保证各运动副正常工作,合理的间隙也是可以存在的,但是会对定位精度产生一定的影响。在遥感器的支撑方案中,间隙的影响是不能忽视的。
运动学设计理论发展已久,比较著名的有精确约束设计,自由度约束拓扑理论和约束螺旋理论等[7]。基于运动学设计理论的机械结构具有运动确定、重复精度高和元件变形小等优点,广泛用于运动学联接及精密定位平台等。进入新世纪以来,许多新的运动学设计理论不断地被提出,应用这些理论解决了大量的工程问题[8-12]。文中采用约束螺旋理论对空间光学遥感器的运动学支撑设计方案展开分析。
1 约束螺旋理论简述[11-12]
1.1 螺旋的概念
如图1所示,空间一条被直线约束的矢量称为线矢量或是节距为零的螺旋,其位置和方向由矢量S 和线距S0决定,S 与S0正交。线矢量的Plücker坐标即(S;S0),表达式为:
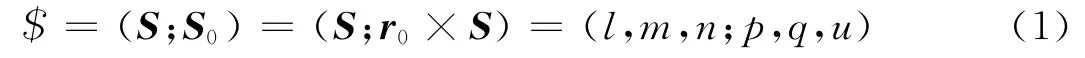
一般情况下,对任意螺旋$=(S;S0),其中,S=r0×S+hS0,h 即为螺旋的节距。节距为零时螺旋便退化为线矢,在运动螺旋系中表示转动副,在反螺旋系中表示约束力。所有空间运动副都可以用螺旋来表达。
1.2 修正的K-G 公式
修正的Kutzbach-Grübler公式表达为:
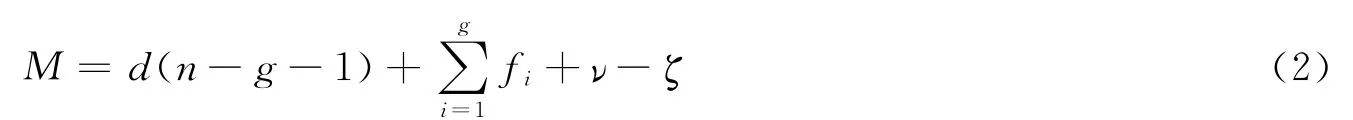
M 表示机构的自由度;n表示包括机架的构件数目;g 表示运动副的数目;fi表示第i 个运动副的自由度;ν表示并联冗余约束数;ζ表示局部自由度数;d 表示机构的阶,也称为公共约束因子。λ为机构的公共约束数。


图1 线矢Fig.1 Line vector
1.3 公共约束和冗余约束
(1)公共约束
并联机构一个分支中的所有运动副形成的螺旋构成一个分支螺旋系,对应此分支螺旋系有一个分支反螺旋系,即分支约束系,它反映了分支约束系统对平台的结构约束。运动平台承受了所有分支的约束螺旋,它们构成平台的约束系,决定了平台的运动。机构的公共约束就是这个机构所有运动螺旋的反螺旋,机构的所有公共约束数为:
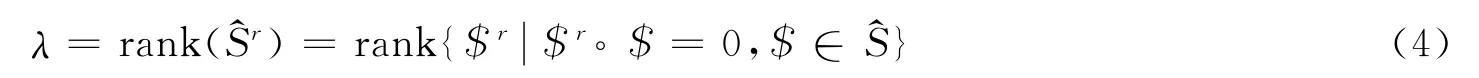
(2)冗余约束
考虑公共约束之外其他的t个约束是否形成冗余约束。当t个约束形成k 系螺旋,k<t时,只有k个螺旋起到约束作用,其余t-k个螺旋为冗余约束,即:

2 遥感器的运动学支撑方案
2.1 结构模型
空间并联机构具备高精度、高刚度、高承载能力等特性,且三点支撑可以达到更高的共面精度。所以,空间遥感器的支撑结构采用对称的3-RRR 空间并联机构,通过三条均匀分布的R-R-R运动支链Ki(i=1,2,3)将机体和遥感器连接起来,其中Sj(j=1,2,3,……,9)为第j个转动副的轴线,编号1,4,7的转动副共面连接机体平台,编号3,6,9的转动副共面连接遥感器的底部平台,以下简称工作平台,编号2,5,8的三个中间转动副共面且轴线成对心分布。每条支链中上下两个转动副平行,与中间的转动副空间垂直,这样可以减小误差累积,降低装配精度对性能的影响。支撑结构示意图如图2所示。
2.2 理想状态自由度分解
采用约束螺旋理论分析支撑结构对工作平台的约束问题。在图2所示坐标系中,支链K1与支链K2关于x-z平面对称,α为S4与z轴夹角,β,θ分别为过点O 做S5和S9的垂线与底部平台的夹角,a,r,d,R,分别为点O 到S4,S5,S7,S9的距离。取支链K1为分支螺旋系I,依次类推,计算分支螺旋系I为:
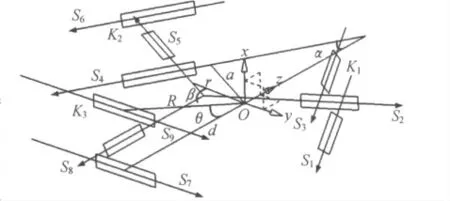
图2 支撑结构示意图Fig.2 Schematic drawing of supporting structure

可得分支螺旋系I的分支反螺旋系为:

工作平台的自由度为:
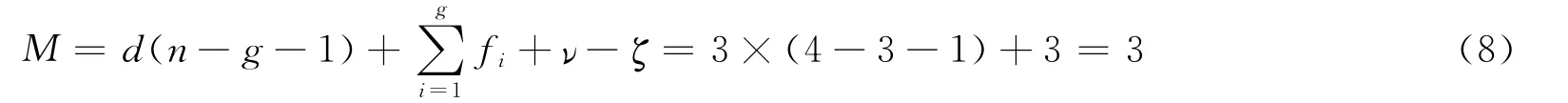
观察这个反螺旋系,三个反螺旋均为线矢,带来三个有效约束,共约束了工作平台沿x 轴的转动,平动,以及在y-z平面内沿着(sinα,cosα)方向的平动,平台还具备三个自由度。
计算分支螺旋系II为:

可求得分支螺旋系II的分支反螺旋系为:
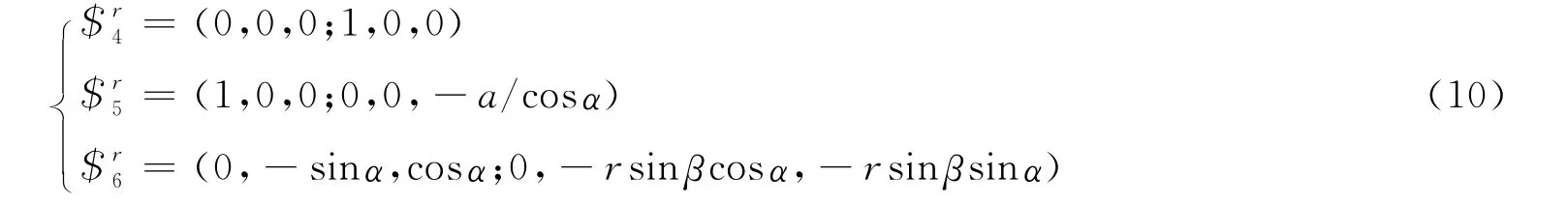
可得工作平台的自由度为:

由表达式(7)和式(10)可以看出,分支反螺旋系II 与分支反螺旋系I 有一个共同的约束螺旋(0,0,0;1,0,0),形成公共约束,其余两个螺旋为有效约束,约束了平台沿z轴方向的转动及在y-z 平面内沿着(-sinα,cosα)方向的平动。至此,约束了平台三个平动自由度和沿着x 轴,z 轴方向的转动自由度,平台只剩下一个沿着y 轴方向转动的自由度。
同理可求得分支反螺旋系III为:
由三个分支反螺旋系可知,该结构具备一个公共反螺旋(0,0,0;1,0,0),支撑结构有一个公共约束,此力偶约束了上平台沿x 轴方向的转动。由于有三个支撑分支,此公共约束包含两个过约束。
除去公共约束后的六个约束螺旋组成了一个五系螺旋,由式(5)可得:

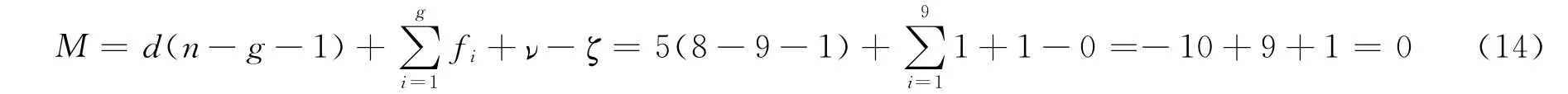
即支撑结构约束了平台的全部六个自由度,同时具备三个过约束。在实际情形中,由于间隙的影响,与理想情况会有所差别。
2.3 引入间隙后自由度分配
为了保证各运动副正常工作,避免过盈联接,构件加工装配后需存在铰间隙。但这些间隙会影响机构的自由度分配,尤其对空间三分支并联机构很明显。
单独考虑每个支撑分支,三个转动副都有间隙,在理想约束允许的运动之外,当工作平台绕x 轴发生微小转动时,会引起工作平台产生空间微小平动。
由式(11)可知,两分支并联机构存在一个自由度,为绕y 轴方向的转动自由度。s实验中,由于间隙的存在诱发了转动副的运动,使工作平台可以绕x 轴方向转动一个小角度。假设两分支中所有转动铰都具备同样的轴向间隙和径向间隙,经ADAMS软件采集数据和MATLAB进行数据处理,可以拟合出间隙与转角大小的关系,见图3所示。由图3可以看出,转角对轴向间隙更为敏感。

图3 间隙与转角的关系Fig.3 Relationship between clearance and rotation angle
3 杆件的优化设计
计算压杆临界压力的公式为:

式(15)也就是欧拉公式的普遍形式,Fcr为临界压力,E 为材料弹性模量,I 为截面惯性矩,l为杆件长度,μl称为相当长度,μ 称为长度因数,μ 值如表1所示。
由于支撑方式已经确定,为了增加杆件的临界压力,增强结构的稳定性,应适当减小杆件的长度,选择合理的截面形状以提高截面惯性矩。为了提高截面惯性矩,可以增加截面面积。在截面面积相同时,适当地把材料放在离截面形心较远处同样能够提高截面惯性矩。这样,空心截面比实心截面更合理。同时,在不影响运动副工作的条件下适当减小杆件长度,可增强稳定性。为了与轴相连接,矩形截面的构件更容易加工,优化后支撑构件的截面采用空心矩形,如图4所示。
优化后的支撑结构如图5所示。
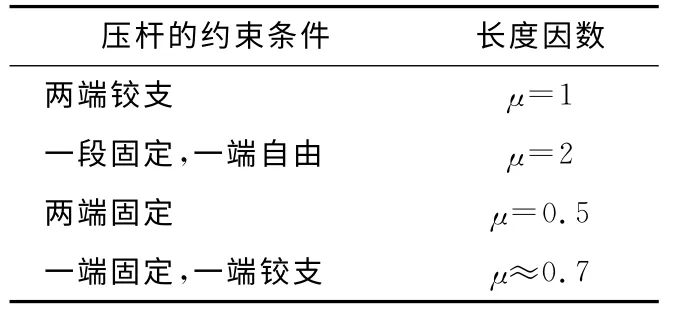
表1 长度因数Tab.1 Length factor

图4 构件结构Fig.4 Configuration of component
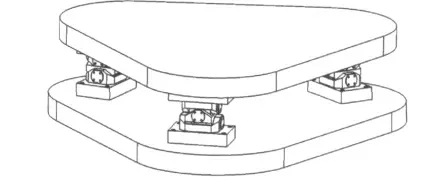
图5 完整支撑结构Fig.5 Integrated support structure
4 实验结果
对加工出符合公差范围与设计尺寸的各部件装配后进行实验。实验中将下平台固定于实验台上,对上平台施加各方向的力和扭矩。实验数据显示,工作平台不具备自由度,因间隙的影响沿各轴的平动位移都在0.01mm数量级,也会产生微小的转角,工作平台沿各轴转角如图6所示。
从图6中可以看出,x,y,z 三个方向能达到的最大转角分别为3.95″,1.86″,1.81″。

图6 工作平台转角Fig.6 Rotation angle of working platform
5 结 论
提出了以3-RRR 空间并联机构作为空间光学遥感器的运动学支撑方案,运用约束螺旋理论分析了支撑结构对工作平台的自由度约束问题,研究了微米级铰间隙对自由度分配的影响,在满足定位要求的前提下,适当增加间隙使运动支撑结构,在装配精度范围内不具备过约束,这样既能降低航天器机体平台精度对遥感器成像性能的影响,又能减少加工和装配误差引起的结构内应力。为了提高稳定性,优化了支撑构件的结构。文中设计的支撑方案在理论和实际中均能够实现对空间光学遥感器的支撑和定位。加工装配后样机的实验结果显示:遥感器相对于机体平台最大平动位移在0.01mm 数量级,绕x,y,z三个轴的方向能达到的最大转角分别为3.95″,1.86″,1.81″,从运动学角度满足了对空间光学遥感器的支撑和精密定位要求。
[1] 贾晓辉,张大卫.三自由度精密定位工作台的设计与运动学分析[J].天津大学学报,2010,43(5):457-463.
[2] 赵 磊,刘 巍,巩 岩.预紧式Stewart结构六维力/力矩传感器[J].光学 精密工程,2011,19(12):2954-2962.
[3] 崔冰艳,金振林.基于正交结构的机器人肩关节静力学分析与结构参数设计[J].光学 精密工程,2011,19(1):77-81.
[4] 王振华,陈立国,孙立宁.集成式6自由度微动并联机器人系统[J].光学 精密工程,2007,15(9):1391-1397.
[5] WALDRON K J.A study of over constrained linkage geometry by solution of closure equations-part I.Method of study[J].Mechanism and Machine Theory,1973,8(2):95-104.
[6] FANG Y,TSAI L W.Enumeration of a class of over constrained mechanisms using the theory of reciprocal screws[J].Mechanism and Machine Theory,2004,39(11):1175-1187.
[7] 王大志,何 凯,杜如虚.精密机械运动学结构设计方法的若干新进展[J].机械设计与研究,2011,27(3):1-4.
[8] HOPKINS J B,CULPEPPER M L.Synthesis of multi-degree of freedom,parallel flexure system concepts via freedom and constraint topology(FACT)-partⅡ:practice[J].Precision Engineering,2010,34(2):271-278.
[9] KOSEKI Y,TANIKAWA T,KOYACHI N,et al.Kinematic analysis of translational 3-DOF micro-parallel mechanism using matrix method[C]∥Proceedings of the 2000IEEE/RSJ International Conference on Intelligent Robots and System,Takamatsu:IEEE,2000:786-792.
[10] ZHAO J S,FENG Z J,ZHOU K,et al.Analysis of the singularity of spatial parallel manipulator with terminal constraints[J].Mechanism and Machine Theory,2005,40(3):275-284..
[11] 黄 真,赵永生,赵铁石.高等空间机构学[M].北京:中国高等教育出版社,2006.
[12] 黄 真,刘婧芳,曾达兴.基于约束螺旋理论的自由度分析的普遍方法[J].中国科学,2009,39(1):84-93.
