三角函数逼近算法及其在光学条纹图像分析中的应用*
2013-03-11郭红卫
周 珺,郭红卫
(上海大学 机电工程与自动化学院,上海 200072)
引 言
三角函数与反三角函数作为基本初等函数,在工程技术与科学研究中有广泛的应用,但在某些特定情况下则需通过逼近函数来计算其近似值。例如,在工业中常采用单片机、硬件计算设备或各种小型系统来实现过程的控制[1],然而这些系统可能并不支持三角函数的库函数计算,那么就需要寻找替代的逼近方法来计算其数值。另外,相对于一般算术运算,三角函数与反三角函数计算复杂度相对较高,计算耗时,难以满足各种实时性要求。例如,在机器人动力学[2]方程的快速计算中,三角函数的计算也占很大的比例[3]。另外,在计算机三维建模与三维游戏中,三维模型的空间坐标变换也涉及到大量连续的三角函数运算[4]。GPU[5]作为一种可编程的图形处理器,利用Vertex Shader计算反三角函数也很浪费时间。在这些情况下,采用三角函数的快速近似计算可以大大提高计算效率[6-7],满足各类实时性要求。
同样,在光学检测技术中,也涉及到大量的三角函数运算。例如,傅里叶变换位相分析方法[8-9]中,大量的复指数运算需通过正余弦函数的计算来实现;相移步距未知情况下的相移算法中,需使用反余弦函数来求解相对相移量[10];各种位相分析方法一般需通过四象限反正切函数逐像素计算条纹图像上的位相分布[11];而在多视角(口径)测量[12-13]中,则需利用坐标变换来实现各视角测量结果的配准与拼接,也要用到大量的三角函数计算。这些计算消耗大量时间,已成为快速测量或实时测量的一个瓶颈问题,同时也使得测量数据的硬件或固件计算处理难以实现。
三角函数与反三角函数的快速近似计算可采用多种方法实现。其中,查表法首先对函数特定区间按特定分辨率进行采样并计算其数值,并建表存储在内存中。使用时,直接访问相应地址即可获得需要的三角函数值。查表法简便易行,效率很高,但需要占用一定的内存空间。特别是当精度要求提高时,所需内存的大小也需相应地增大。泰勒级数也常被用来计算函数的近似值。根据泰勒定理,一个无限可微函数可由其泰勒展开式无限逼近。但泰勒级数收敛较为缓慢,无法实现低阶高精度的逼近。例如在区间[-1,1]上用泰勒级数计算反正切函数值时,若要精度达到10-3数量级,需将其展开至49阶;若要精度达到10-4数量级,则需将其展开至499阶。这一现象说明,当精度要求较高时,泰勒级数并不是一种实用有效的函数逼近方法。另一种方法是采用最小二乘多项式逼近三角函数,该多项式与目标函数之间的平方距离可达到极小值。由于最小二乘多项式系数的计算十分简单,该方法较易于实现。采用这种方法,仅需5阶和7阶多项式即可分别使上述区间内的反正切函数的求解精度达到10-3和10-4数量级,其逼近效率远高于泰勒级数法。但是,这种最小二乘多项式并非是最优的。换言之,存在阶数更低的多项式可达到相同的精度。不同于上述方法,本文讨论三角函数及反三角函数的最佳逼近方法,推导了基于无穷范数的最佳逼近多项式。
1 三角函数逼近算法
1.1 原理
假设y=f(x)是区间[x1,x2]内的连续函数,该区间其N 阶逼近多项式可表示为:

pn(n=0,1,…,N)为其系数。该方程涉及N(1+N)/2次乘法和N 次加法运算。为简化,式(1)可改写为:


对于具体的三角函数,首先针对其某一特定区间[x1,x2]求解逼近多项式,然后再将其结果推广到整个2π周期区间。根据数值分析理论,f^(x)-f(x)在闭区间[x1,x2]内至少有N+1个不同的根(根的集合可能包含x1和x2),在开区间(x1,x2)内至少有N 个交错极值点,其极值的绝对值相等正负号交替。当将区间[x1,x2]上的逼近方程拓展到区间外时,不仅要保证分段逼近函数在整个函数定义区间内尽可能是最优的,而且要保证其在整个定义区间上的连续性。为此要求,在选定区间[x1,x2]的边缘处,多项式与函数f(x)的关系满足一定条件。假设x=xi(i=1或2)是一个边缘点。如果函数f(x)关于x=xi左右对称则在x=xi处有一个附加的交错极值点,即:

其中,η为极值。关于极值的正负号,当i=1(左边缘点)时,m=0,当i=2(右边缘点)时,m=N+1。如果函数f(x)在x=xi处非左右对称,则强制要求与f(x)精确相等,即:

第1步:任选N 个点ξk(k=1,2,…,N),满足x1<ξ1<ξ2<…<ξN <x2。
第2步:假设差值f^(ξk)-f(ξk)(k=1,2,…,N)具有相等的绝对值和交错的正负号,即:
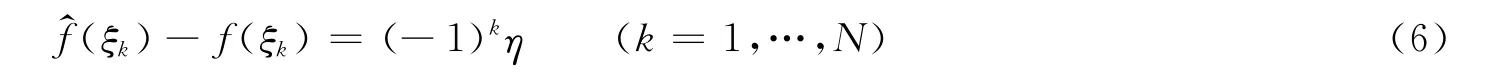
将式(6)与式(4)或式(5)联立形成一个包含N+2个方程式的线性方程组,该方程组包含pn(n=0,1,…,N)和η共N+2个未知数。
第3步:利用第二步计算所得系数pn构建多项式。解方程:

这种方法可以构建出一个函数在区间[x1,x2]内的逼近多项式。利用该方法可以推导出基本的三角函数(正弦,正切)及其反函数在特定区间内的逼近多项式,然后再将其结果拓展至整个2π周期或整个函数定义区间。
1.2 结果和讨论
1.2.1 余弦函数逼近
正弦和余弦函数是两种基本的三角函数。因为sin(x)=cos(π/2-x),正弦函数sin(x)可以由通过余弦函数cos(x)求得,所以只需针对余弦函数进行讨论。余弦函数是一个定义在(-∞,+∞)内的周期函数,利用上述方法可以在一个基本周期[0,2π]内求解其逼近多项式。但是这种分段方式无法获得效率较高的逼近方程。例如,采用4次逼近多项式,最大误差达到0.035;若要使逼近精度达到10-3数量级,多项式次数至少为6次。这意味着执行较多的乘法运算,要消耗较多的计算时间。因此,函数逼近区间局限在[0,π/2]范围内,最后通过三角恒等式得到整个周期上的分段逼近多项式。采用第2.1节所述的方法,对[0,π/2]区间内的余弦函数进行多项式逼近。由于余弦函数是偶函数,在区间左边界x=0处,采用式(4)作为边界条件;而在右边界x=π/2处,以式(5)作为边界条件。计算所得的3至5次多项式系数及最大误差如表1所示,其中pn为式(1)所定义的多项式的n次项系数。

表1 区间[0,π/2]内余弦函数逼近多项式系数和最大误差Tab.1 Coefficients and maximum errors of approximation polynomials for the cosine function in[0,π/2]
整周期[0,2π]区间内的余弦函数则可以利用上述逼近多项式,以分段逼近多项式计算得到,即

1.2.2 正切函数逼近
正切函数tan(x)是一个周期函数。在周期(-π/2,π/2)之内,当x 趋近于±π/2 时,该函数取值趋近于±∞。在整个周期上就无法获得正切函数单一的最佳逼近多项式。但是可以选取一个相对较小的区间计算其逼近多项式。例如,表2所示是采用1.1节方法求得的正切函数在[0,π/2]之间的逼近多项式的系数及最大误差。为保证连续性,计算采用的边界条件由式(5)确定。
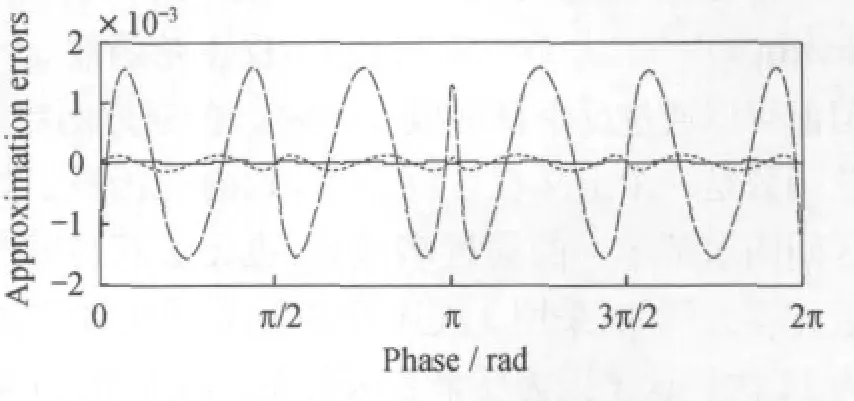
图1 余弦函数3次(短划线)、4次(点线)和5次(实线)分段逼近多项式误差Fig.1 The approximation errors of cos(x)with polynomial degree being 3(dashed),4(dot)and 5(solid lines)

表2 区间[0,π/4]内正切函数逼近多项式系数与最大误差Tab.2 Coefficients and maximum errors of approximation polynomials for the tangent function in[0,π/4]
利用上述[0,π/4]区间内的逼近多项式,有多种方法可以实现整个周期区间内的正切函数的近似计算。第一种方法就是利用三角恒等式,可得:
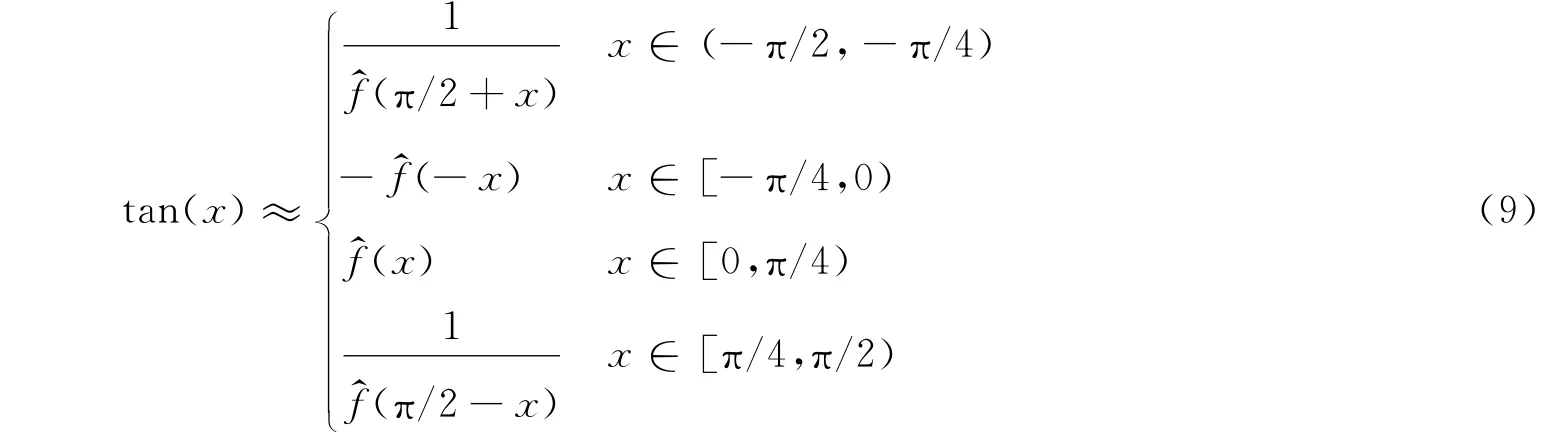
式(9)表示正切函数在一个整周期(-π/2,π/2)上的分段逼近函数。其误差分布如图2所示。从中可见,根据式(9)所得正切函数近似值在一个周期内仍然是连续分布的。在[-π/4,π/4]区间上最大逼近误差被最小化,其逼近函数是最佳逼近。但是,在[-π/4,π/4]区间之外,误差分布是不均匀的,这种逼近不再是最佳逼近。特别是在靠近周期边缘处,当接近π/2时,误差增大较快。这是由于正切函数在此处趋近于∞的性质决定的。
第二种获取整周期函数的方法是利用前述正弦函数sin(x)和余弦函数cos(x)的逼近多项式,通过三角关系式tan(x)=sin(x)/cos(x)进行计算。模拟实验证明在接近±π/2处,这种方法精度略高于第一种方法,但是其误差仍然不是均匀分布,这种方法也不是最优的,并且需要执行较多的乘法运算。实际上,正切函数在(-π/2,π/2)周期内不存在一个最佳逼近多项式或分段的最佳逼近多项式。在具体应用中,所要求解的正切函数角度范围往往被限制在一个较小的已知区间内,此时就可以利用1.1节所述方法直接求解该区间内的最佳逼近多项式。
1.2.3 反余弦函数逼近
反正弦和反余弦函数是两种基本的反三角函数。因为arcsin(x)=π/2-arccos(x)成立,反正弦函数arcsin(x)的近似值可以通过反余弦函数arccos(x)的逼近函数求得。反余弦函数是一个定义在区间[-1,1]内的函数。如果在整个区间内求解单一的逼近多项式,也无法获得效率较高的逼近方程。例如,采用3次逼近多项式,最大误差达到0.14;若要使逼近精度达到10-4数量级,多项式次数至少为11次。这是因为反余弦函数在x趋近于±1时,导数趋近于±∞,这就要求采用非常高阶的多项式才能逼近该曲线。采用高阶多项式意味着需执行更多的乘法运算,消耗更多的时间。因此,将函数逼近的区间局限在范围内,最后通过三角恒等式得到整个定义域上的分段逼近多项式。
采用1.1节所述的方法,以式(5)为边界条件,分别用1、3、5次多项式对区间内的余弦函数进行多项式逼近,所得的多项式系数及最大误差如表3所示。

图2 正切函数的3次(短划线)和5次(实线)分段逼近多项式误差Fig.2 The approximation errors of tan(x)with polynomial degrees being 3(dashed)and 5(solid lines)
表3 区间内反余弦函数逼近多项式的系数和最大误差Tab.3 Coefficients and maximum errors of approximation polynomials for the arccosine function in

表3 区间内反余弦函数逼近多项式的系数和最大误差Tab.3 Coefficients and maximum errors of approximation polynomials for the arccosine function in
多项式的 多项式系数 最大逼近次数p0 p1 p2 p3 p4 p5误差/rad 1 π/2 -1.110 720 0.033 00 3 π/2 -1.019 450 0.126 854 -0.361 939 0.000 87 5 π/2 -1.002 146 0.036 749 -0.364 830 0.432 948 -0.420 863 0.000 038
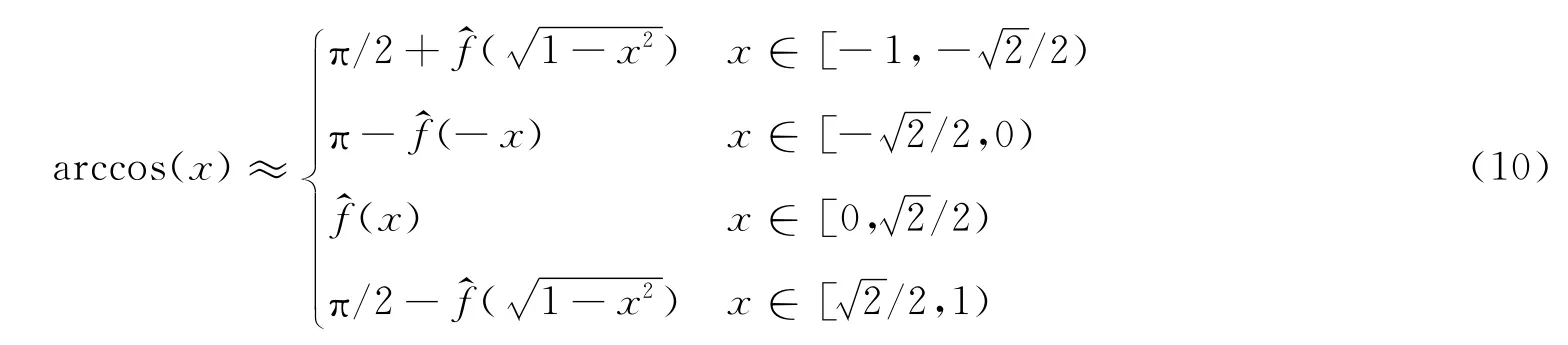
可以看出式(10)所得到的逼近多项式在各分段边界处是连续的,在各个分段区间内的最大误差是一致的。与前述整个定义区间上单一的逼近多项式相比,其多项式次数较少,计算量要小得多。
1.2.4 反正切函数逼近
反正切函数arctan(x)是定义在(-∞,+∞)上的奇对称函数,无法获得整周期内的单一逼近多项式。为此可以选取一个小区间计算其逼近多项式,再把其拓展到整个区间。表4 所示是采用1.1 节方法,以式(5)为边界条件,求得的正切函数在[0,1]之间的逼近多项式的系数及最大误差。从表中可见,由于反正切函数的奇对称性质,这些多项式的0次项(常数项)为0。
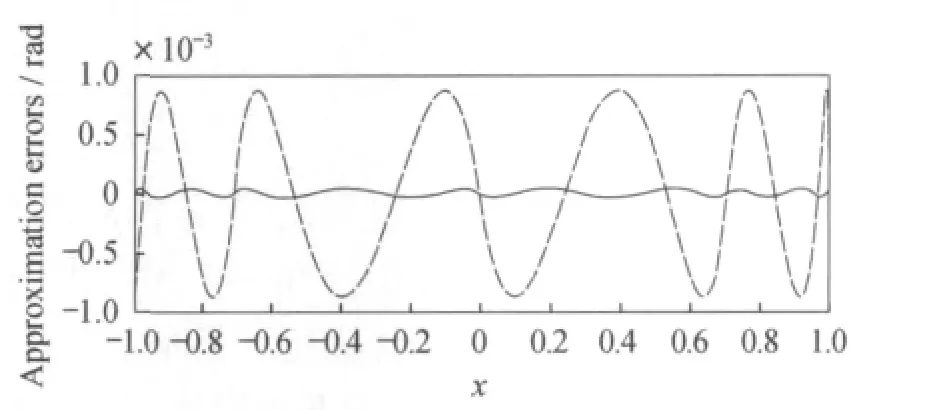
图3 反余弦函数的3次(短划线)与5次(实线)分段逼近多项式误差Fig 3 The approximation errors of arccos(x)with polynomial degrees being 3(dashed)and 5(solid lines)

表4 区间[0,1]内反正切函数逼近多项式的系数和最大误差Tab.4 Coefficients and maximum errors of approximation polynomials for the arctangent function in[0,1]
得到区间[0,1]内的逼近多项式后,整个定义域区间(-∞,+∞)内的反余弦函数可以利用分段逼近多项式计算得到,即:

图4显示在使用3次与5 次逼近时误差的比较。可以看出式(11)所得到的逼近多项式在各分段边界处是连续的,在各个分段区间内的最大误差是一致的。
2 应 用
2.1 条纹分析算法
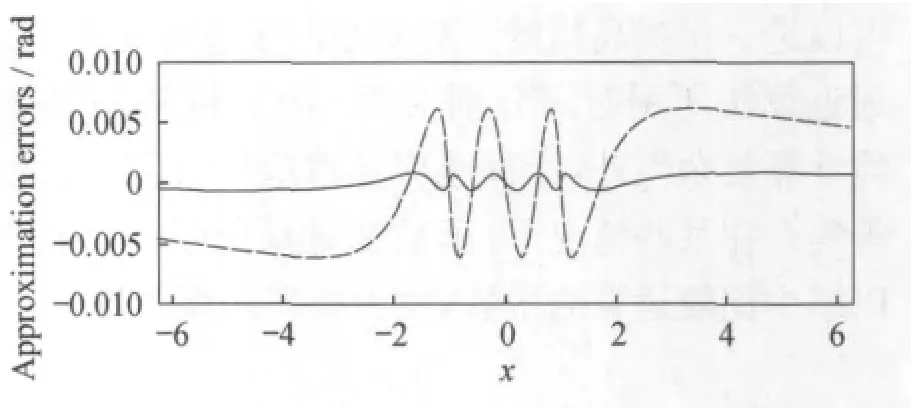
图4 反正切函数的3次(短划线)与5次(实线)分段逼近多项式误差Fig 4 The approximation errors arctan(x)with polynomial degrees being 3(dashed)and 5(solid lines)
光学三维测量技术常以二维条纹图像的形式提供其原始测量数据[14-15]。其中,第三维信息就包含于条纹图像的位相之中。因此,分析条纹的位相信息是实现光学测量的关键步骤,其中涉及大量的三角函数计算。下面以相移步距未知情况下的相移算法为例来说明本文方法在条纹图像分析中的应用。当相移步距未知并沿图像为不均匀分布时,第k 幅相移条纹图可表示为

其中,(x,y)是图像像素坐标;Ik、a和b 分别表示光强、背景光强与调制度;位相φ 与相对相移量α 均为未知量。条纹分析的第一步是针对每一像素估计其相对相移量:

再利用最小二乘相移算法求解位相。解方程组:
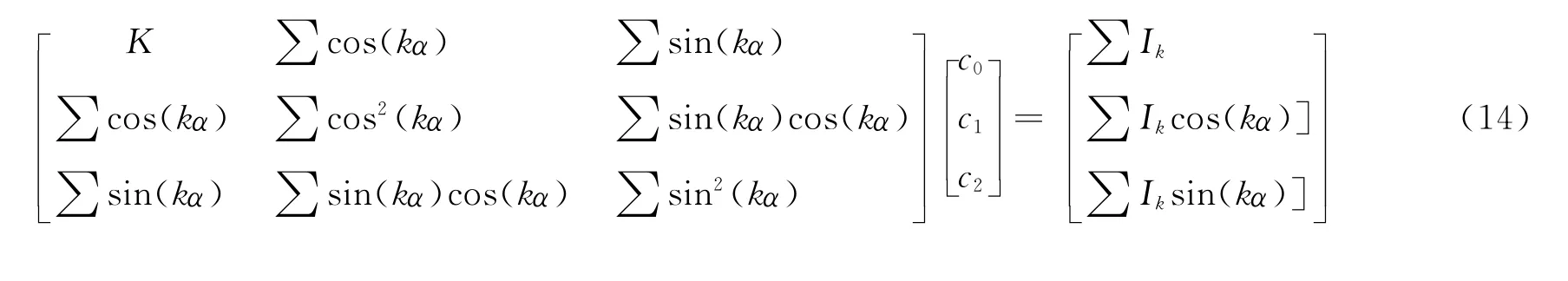
则各像素的位相为

上述过程对每一像素点来说总共涉及2 K 次的正弦或余弦计算,一次反余弦计算和一次反正切计算。这些运算都可以利用本文方法计算,以简化计算。
2.2 实验
上述相移步距未知情况下的相移算法,适用于汇聚光相移干涉测量[16]、阴影莫尔形貌测量[17]、镜像莫尔形貌测量[18]等。在这些方法中,位相与相移量均依赖于被测表面的深度或梯度等形貌信息,因而未知且呈非均匀分布。图5所示为一幅相移镜像莫尔条纹图。总相移步数为K=64。图6比较了条纹分析的结果。图6(a)和6(b)为通过式(13),分别利用标准反余弦函数及其逼近算法计算所得相对相移量。其中,逼近多项式阶数为3,系数见表3。图6(c)显示两者的差值,说明逼近方法误差小至10-4数量级。图6(d)和6(e)为通过式(14)与式(15),分别利用标准三角函数及其逼近算法计算所得包裹位相。其中,逼近多项式阶数为3,余弦函数逼近多项式系数见表1,反正切函数逼近多项式系数见表4。图6(f)为两者之差,从中可见,采用3阶多项式逼近算法,导致的最大位相计算误差仅为0.027rad。采用更高阶多项式,可以进一步提高精度。对整幅图像进行处理,采用标准函数算法与逼近算法所用时间分别为45.70s和39.15s。后者略快于前者。除计算复杂性外,计算速度还取决于计算机性能,程序代码的优化等等。在某些情况下,函数变量局限于一个较小的已知区间时,可以减少比较运算的次数,大大提高计算的效率。

图5 莫尔条纹图Fig 5 A Moiréfringe pattern

图6 条纹图像分析结果Fig 6 Fringe pattern analysis results
3 结 论
在三角函数及反三角函数的特定区间内推导了基于无穷范数的最佳逼近多项式,得到了各个三角函数和反三角函数分段的多项式。利用三角函数的关系式将这些三角函数推广到整周期区间,或利用反三角函数的关系式将这些反三角函数推广到整个定义区间。文中也给出了一定精度内的各函数逼近多项式的系数及最大误差。将上述结果应用于光学条纹图像的分析,通过实验证明了方法的有效性。所述三角函数逼近算法,由于只是涉及一些简单的逻辑和算术运算,非常适合于光学测量信息处理中硬件与固件计算的实现。另外,在一些具有实时性要求的应用中,可以替代库函数运算,提高计算速度。此外,这些结果具有普遍性,也可用于其它科学研究及工程应用目的。
[1] 胡天亮,张洪波,刘日良.基于STEP-NC的数控车削系统的加工工艺参数优化[J].工艺与检测,2011(8):128-131.
[2] 魏振忠,张 博,张广军.双机器人系统的快速手眼标定方法[J].光学 精密工程,2011,19(8):1895-1902.
[3] 于华东,方 滨,周东辉.一种机器人动力学方程快速计算的三角函数发生器[J].机器人,2002,24(6):7-9.
[4] BELLIS S J,MARNANE W P.A CORDIC arctangent FPGA implementation for ahigh-speed 3D-camerasystems[J].Lecture Notes in Computer Science,2000,1896:485-494.
[5] 许 桢.关于CPU+GPU 异构计算的研究与分析[J].科技信息,2010(17):613.
[6] 李加文,陈宗雨,李从心.基于函数逼近的三角函数加减速方法[J].机床与液压,2006(3):66-67.
[7] 郭新贵,李从心.一种新型柔性加减速算法[J].上海交通大学学报,2003,37(2):205-207.
[8] TAKEDA M,MUTOH K.Fourier transform profilometry for the automatic measurement of 3-D object shapes[J].Appl Opt,1983,22(24):3977-3982.
[9] TAKEDA M,INA H,KOBAYASHI S.Fourier transform method of fringe-pattern analysis for computer-based topography and interferometry[J].J Opt Soc Am,1982,72(1):156-160.
[10] GUO H W,CHEN M Y.Least-squares algorithm for phase-stepping interferometry with an unknown relative step[J].Appl Opt,2005,44(23):4854-4859.
[11] GUO H W,LIU G Q.Approximations for the arctangent function in efficient fringe pattern analysis[J].Opt Express,2007,15(6):3053-3066.
[12] GUO H W,CHEN M Y.Multiview connection technique for 360-deg three-dimensional measurement[J].Opt Eng,2003,42(4):900-905.
[13] HE H T,CHEN M Y,GUO H W,et al.Novel multiview connection method based on virtual cylinder for 3-D surface measurement[J].Opt Eng,2005,44(8):083605.
[14] 陶 涛,郭红卫,何海涛.镜面反射面形光学三维测量技术综述[J].光学仪器,2005,27(2):90-95.
[15] 蒋尊兴,郭红卫,陈明仪.自适应空间载波相移算法[J].光学仪器,2006,28(6):54-58.
[16] ROBINSON D W,REID G.Interferogram analysis:digital fringe pattern measurement[M].Bristol:IOP,1993:94-140.
[17] LADAK H M,DECRAEMER W F,DIRCKX J J J,et al.Systematic errors in small deformations measured by use of shadow-Moire topography[J].Appl Opt,2000,39(19):3266-3275.
[18] GUO H W.Phase-shifting deflectometric Moirétopography[J].Structural Longevity,2011,5(1):
39-48.
