具有分布时滞的随机中立型系统的随机鲁棒镇定

汪 慧， 丁 健

（安徽新华学院 公 共课教学部，安徽 合 肥 230088）

0 引 言

工业技术、社会经济和生物工程等领域存在的许多问题，其动态规律皆可用确定模型和随机模型来描述。在理想状态下，系统经常表述为确定性模型。当对系统研究有较高的精度要求时，必须充分考虑随机因素的影响。而现实系统中由于传输、测量等各类因素的影响，普遍存在着时滞现象，这常常是引起系统不稳定的重要因素之一。目前对于中立型系统的研究成果已经推广到随机中立型系统，如文献［1－2］对随机中立型系统的鲁棒控制进行了研究，文献［3］给出了随机时滞中立系统的L2－L∞滤波设计的充分条件。在实际运用中由于种种因素均会造成控制器实现过程中参数发生一定程度的变化，结果往往会导致原来稳定的闭环系统失去稳定性。因此，对不确定随机中立系统的研究逐步成为研究的热点。文献［2］研究了不确定随机中立系统的随机鲁棒镇定和H∞控制问题，文献［4］又对此类系统的全局渐近稳定性给出了结论。近年来，文献［5］提出了具有分布时滞的随机中立系统的随机鲁棒镇定和H∞控制问题，并给出了充分条件。虽然对此类时滞系统的控制器的研究已经有很多［6－9］，但对于不同时变时滞的不确定随机中立系统的鲁棒镇定问题研究报道尚少，有广泛的研究空间。

本文关注的是同时具有离散和分布的时变时滞的不确定随机中立型系统的随机鲁棒镇定问题。针对一类在状态项含时变时滞，状态项和控制项都含不同时变时滞，且不确定参数是有界范数的随机中立型时滞系统，利用随机Lyapunov稳定性理论和It＾o微分法则，采用线性矩阵不等式方法，推导出系统的随机渐近稳定的充分条件，并进一步给出随机鲁棒可镇定的充分条件。镇定控制器主要采用状态反馈的方法设计，从而保证了闭环系统的渐近稳定性。

1 问题描述与准备

考虑如下一类具有分布时滞的不确定随机中立系统：

其中，x（t）∈Rn为系统状态变量；u（t）∈Rm为控制输入；y（t）∈Rq为控制输出；φ（t）为定义在时域区间L2F0（［－d，0］；Rn）连续的初始实函数；w（t）为定义在概率空间（Ω，F，Ρ）上的一维零均标准维纳过程。假定：

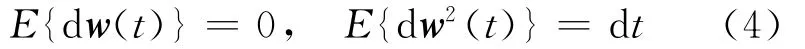
在系统（1）中，d1（t）、d2（t）和d3（t）表示系统随时间变化的未知时滞，且满足：

其中，d2、d3、μ和μ1为已知的正实数。

其中，A1、A2、A3、B1、D、F1、F2、F3为已知适维常数矩阵；A1、A2、A3、B1是连续适维的时变不确定参数，且满足匹配条件：

其中，M、L1、L2、L3、L4为已知常数实矩阵；F（t）为具有Lebesgue可测量元素的适维时变未知矩阵，并且满足：

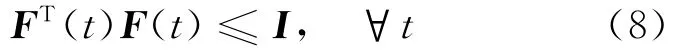
假设矩阵D满足ρ（D）＜1，其中ρ（D）为矩阵D的谱半径。

定义1 对系统（1），当u（t）＝0时，若在任意初始条件下，有‖x（t）‖2｝＝0成立，则称系统（1）是均方渐近稳定的（随机渐近稳定）。

则称在均方条件下，满足（7）式、（8）式的含适维不确定参数的系统（1）随机鲁棒镇定。

（1）S＜0。

（2）s11＜0，s22

（3）s22＜0，s11

引理2 对给定的适当维数矩阵X＝XT，U，V，W，且对所有的V满足VTV≤I，有X＋UVW＋WTVTUT＜0，当且仅当存在一个指标ε＞0，使得X＋ε－1UUT＋εWTW＜0。

引理3 对任意的正定矩阵M，实数γ＞0，以及任意可微的向量函数f：［0，γ］→Rn，则有下式成立，即

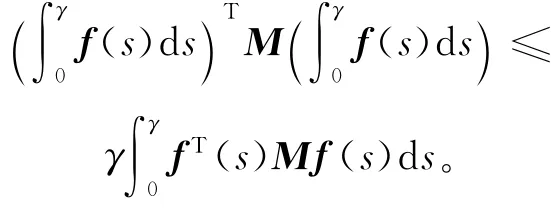
本文研究目的如下：

（1）当控制输入u（t）＝0时，寻找系统（1）随机渐近稳定的充分条件。

（2）构造适当的状态反馈控制器，即

其中K∈Rm×n为状态反馈控制器增益，在此控制器的作用下，使得闭环中立随机分布时滞系统为：

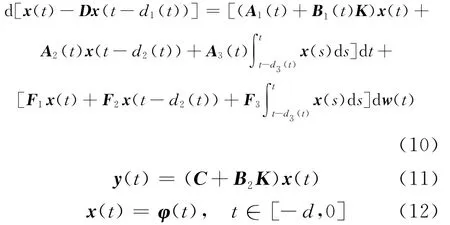
对任何不确定性在均方意义下为随机鲁棒镇定。

2 主要结果

首先考虑的是u（t）＝0时系统（1）的随机渐近稳定性，研究在状态反馈控制器u（t）＝Kx（t）作用下的随机鲁棒镇定。

定理1 对于系统（1），当u（t）＝0时，具有随机渐近稳定性的充分条件是：如果存在正定矩阵P、Q、R、S、U及实数标量d2＞0，d3＞0，u＞0，u1＞0，ε＞0，使得如下的线性矩阵不等式成立：

其中，＊表示对应元素的转置矩阵。

证明 系统（1）可改写为：

其中

同时，可把系统（1）计为：

建立如下的Lyapunov函数：

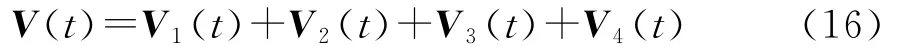
其中

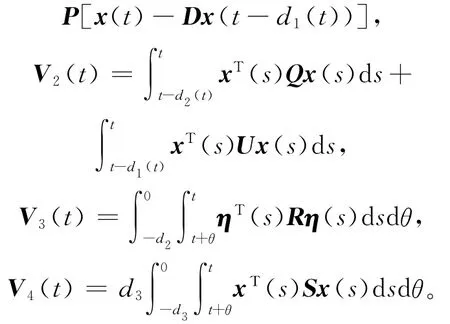
当u（t）＝0，沿着系统（1）的轨迹，运用It＾o微分法则，对（16）式取导，得

由引理3易知：

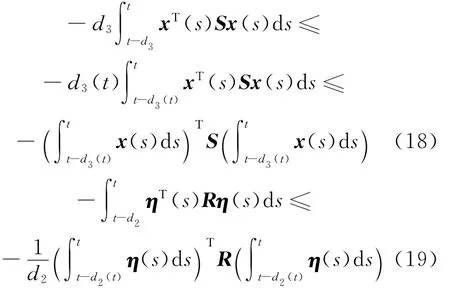
再把矩阵P前置，结合（14）式、（15）式，易知：

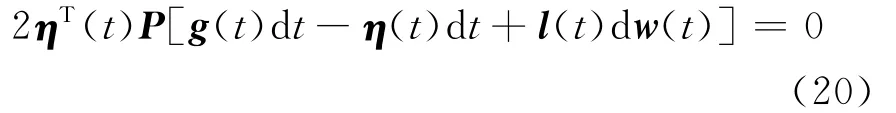
把（18）～（20）式代入（17）式，得

由（21）式可得：

由引理1可知Γ等价于：

由（6）～（8）式及引理1和引理2，知

其中

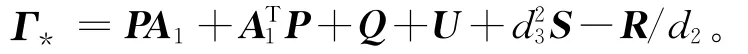
则由（13）式知，Γ≤Υ＜0时可以保证LV（t）＜0，即当u（t）＝0，系统（1）具有随机渐近稳定性。

定理2 考虑不确定中立随机分布时滞系统（10），若存在正定矩阵P、Q、R、S、U及实数标量d2＞0，d3＞0，u＞0，u1＞0，ε＞0，满足以下线性矩阵不等式：

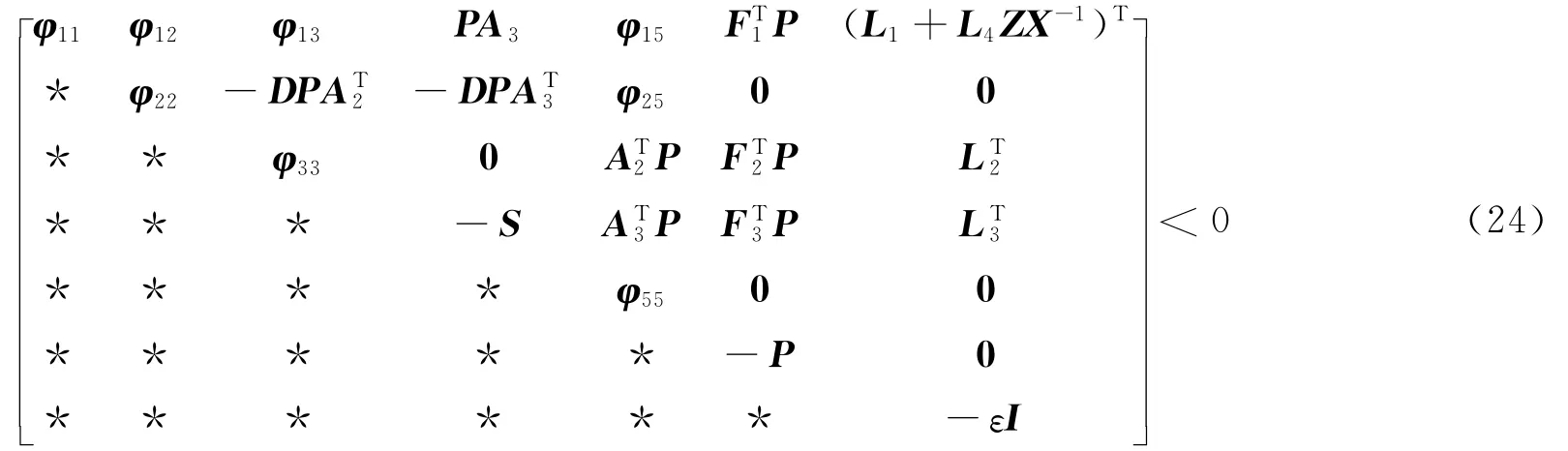
其中

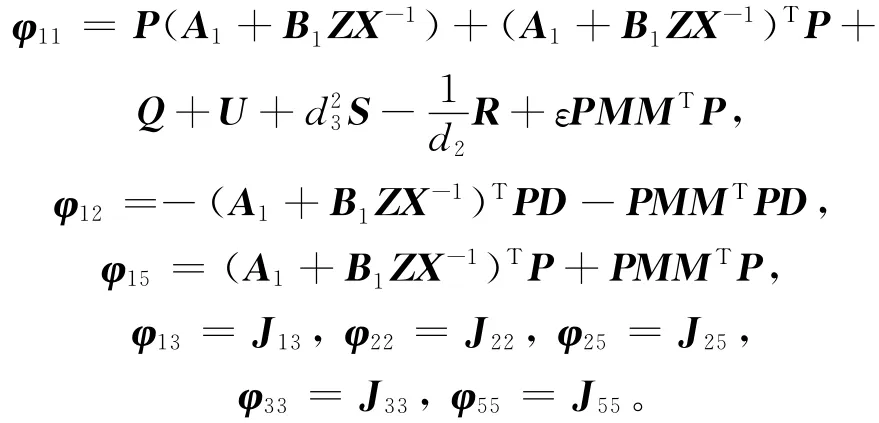
则存在状态反馈控制率u（t）＝Kx（t），K＝ZX－1，在此控制器作用下，对于任何时滞和不确定项，闭环不确定中立随机分布时滞系统（10）在均方意义下为随机鲁棒稳定。

具体证明与定理1类似，故略。

3 数值算例

考虑不确定时变时滞随机中立系统（1），系统参数如下：

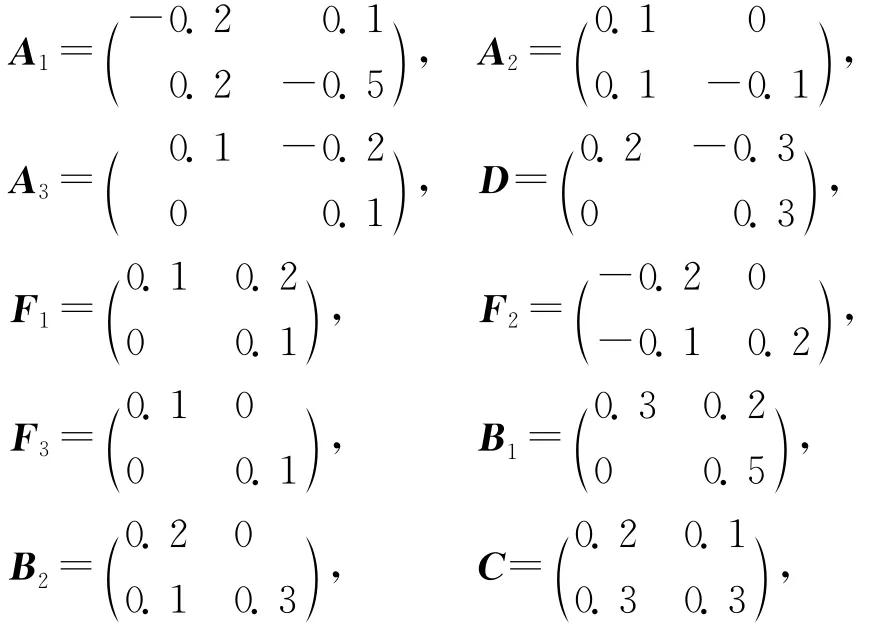
选择满足系统（10）的参数，d2＝0.5，d3＝0.4，u＝0.6，u1＝0.2。

运用Matlab中的LMI工具箱，可得：

4 结束语

本文研究了一类同时具有离散和分布的时变时滞的不确定随机中立型系统的随机鲁棒镇定问题。针对一类同时具有3个时变时滞的且不确定参数是有界范数的随机中立型时滞系统，利用随机Lyapunov稳定性理论和It＾o微分法则，推导出系统的随机渐近稳定的充分条件，并进一步给出随机鲁棒可镇定的充分条件和镇定控制器的设计方法。文中研究结果以线性矩阵不等式的形式给出，数值算例表明了此控制器设计方法的正确性和适用性。

［1］ Lu C Y，Tsai J H，Su T.Robust stabilization of uncertain stochastic neutral systems with multiple delays［C］／／Proceedings of the American Control Conference.Anchorage，America：IEEE American Automatic Control Council，2002：2044－2045.

［2］ Xu S Y，Shi P，Chu Y M，et al.Robust stochastic stabilization and H∞control of uncertain neutral stochastic time－delay systems［J］.Math Anal Appl，2006，314（1）：1－16.

［3］ Lin Li，Yimgmin Jia，et al.L2－L∞filter design for neutral stochastic time－delay systems［C］／／49th IEEE Conference on Decision and Control.December 15 － 17，2010：4132－4136.

［4］ Sun W，Chen Y.Global asymptotic stability analysis for neutral stochastic neural networks with time－varying delays［J］.Commun Nonlinear Sci Numer Simul，2009，14：1576－1581.

［5］ Qiu Jiqing，He Haikuo，Shi Peng.Robust stochastic stabilization and H∞control for neutral stochastic systems with distributed delays［J］.Circuits Syst Signal Process，2011，30：287－301.

［6］ Gershon E，Shaked U.H∞output－feedback control of discrete－time systems with state－multiplicative noise［J］.Automatica，2008，44（2）：574－579.

［7］ Gao Z，Shi X.Robust stability and controller design for uncertain stochastic DAE systems［J］.Journal of Computational Information Systems，2008，5（2）：895－902.

［8］ 王华强，石荣荣，杨滁光，等.一类时变时滞系统的稳定性判据［J］.合肥工业大学学报：自然科学版，2011，34（8）：1146－1451.

［9］ Park J H.On the design of observer－based controller of linear neutral delay－differ ential systems［J］.Applied Mathematics and Computation，2004，150（1）：195－202.