GPS长距离高程传递方法研究

成国辉,谭奇峰

(1.中南大学地球科学与信息物理学院,湖南长沙 410083； 2.长沙市规划勘测设计研究院,湖南长沙 410007)

GPS长距离高程传递方法研究

成国辉1,2∗,谭奇峰2

(1.中南大学地球科学与信息物理学院,湖南长沙 410083； 2.长沙市规划勘测设计研究院,湖南长沙 410007)

基于“移去-恢复”原理，借助GPS天文水准理论，本文提出了一种GPS高程传递方法。首先，通过重力场模型移去高程异常中的低频部分，得到似大地水准面的残余面；其次，通过二次曲面拟合，获取似大地水准面的残余面形状和夹角偏差，并计算基准高程点和观测点间剩余高程异常差；最后，获取两点间正常高差。试验表明，该方法可获得三等水准测量的高程传递精度，对长距离高程传递，如跨河、跨海高程传递具有借鉴作用。

“移去-恢复”法；GPS水准；高程异常；夹角偏差；正常高

1 引 言

目前长距离高程传递方法主要有液体静力水准法、常规大地测量水准法和GPS水准法。静力水准法主要采用连通管进行高程传递,但技术要求高,费用昂贵,实施难[1]；常规大地测量水准法采用精密水准或者三角高程测量实现高程传递,由于受大气光学折射等气象条件影响,测量精度较低[2]；GPS水准法通过拟合局部似大地水准面计算观测点正常高,实际上的似大地水准面是一个受多因素影响的,很不规则,因此该方法在某个测区拟合效果好,在另一个测区拟合效果并不满意[3]。为此,基于“移去-恢复”原理[5]和天文水准方法,本文提出了一种高精度长距离高程传递方法。下面具体介绍这种方法的工作原理及实施过程。

2 基本原理

设GPS实测大地高为H,基于似大地水准面的正常高为h,高程异常为ζ。则大地高H与正常高h存在如下关系[4]:

根据ζ变化的物理机制,可将其分为低频部分ζGM和高频部分ζ△[5],如图1所示。

图1 残余面示意图

根据式(1),基准高程点1和观测点2的大地高和正常高之间则存在式(2)关系:

将式(2)中的两式相减并整理即可得到观测点与基准高程点的正常高高差为:

由式(3)知,在已知基准高程点和观测点的大地高后,实现长距离高程传递的关键在于获取和。通过全球重力场模型可分别计算基准高程点和观测点上高程异常的低频部分M和,继而计算得到。似大地水准面上每个点向下移动可获取一个面,即残余面。确定的关键是得到残余面的形状,而残余面的法线向量与椭球面的法线向量的夹角(即夹角偏差)是反映残余似面形状的关键参数。椭球面一定时,该夹角只与残余面形状有关,不受高程系统起算基准的影响[3]。因此,根据高程异常高频部分拟合残余面,再由此计算相应的角度偏差,根据推导的公式得到下面分别介绍这些参数的确定。

2.1 基于全球重力场模型计算ζGM

根据地球重力场模型,地面点P(r,θ,λ)的扰动重力位T为:由布隆公式可得:

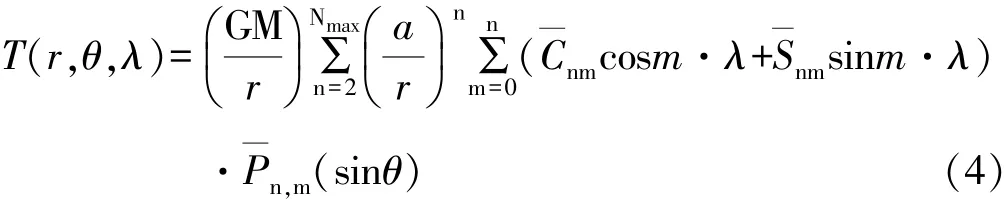
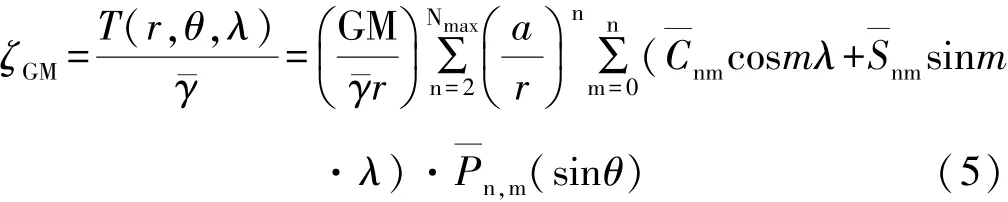
(1)残余面上高程传递原理

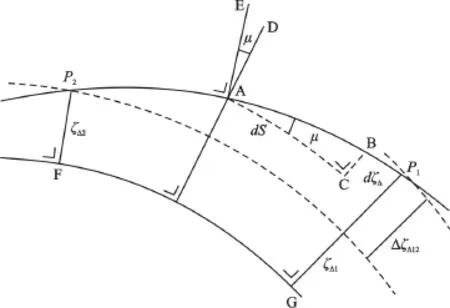
图2 残余面上高程传递原理图

若椭球面法线与残余面法线夹角为θ,其在过点A的P1P2法线面上投影分别为AD和AE,夹角变为μ。在残余面上取P1、P2方向上距离为dS的A、B两极近点,过A点做椭球面的平行面,与B点的正交点为C,圆弧AC可视为距离为dS的直线。由空间几何关系知,AE与AB正交,AD与AC正交。由图2可知,∠BAC=μ,dζ△=-ds tgμ=-μds,则P1、P2两点间的ζ△之差可表达为式(6)。

式中,μ(s)为夹角偏差在P1P2基线上关于距离S的函数。

若残余面变化较平缓,可视μ(s)在P1P2间线性变化,μ1和μ2为P1、P2两点夹角偏差在其基线上的分量,则有:

(2)角度偏差的获取

由于拟合区域相对较小(比如r≤5 km),可将区

域椭球面视为平面[6],其与残余面关系如图3所示。

图3 角度偏差示意图

图3 中,椭球面法向量为→n=(0,0,1),残余面ζ△(x,y)法向量为→s,二者夹角为θ,即有:

如图4,若sx、sy和sz为向量→s在X、Y和Z轴上分量,则θ在X、Y轴上分量α、β为:

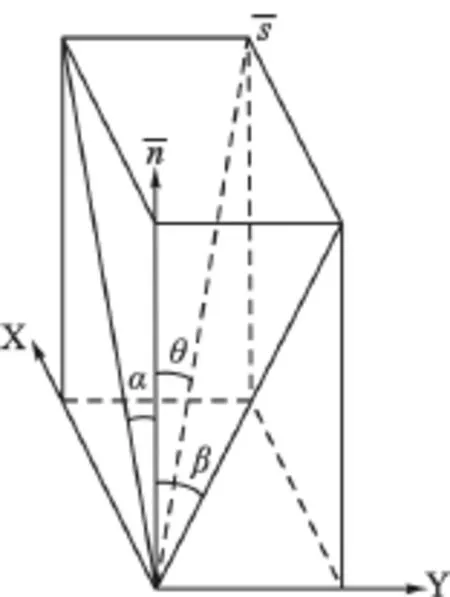
图4 角度偏差分量图

因→n与→s间夹角为小角,故有tanα≈α,tanβ≈β,即有:

则根据文献[4],夹角偏差θ在大地方位角为φ的投影面上的投影分量:

由式(10)和(11)知,要获得夹角偏差,则首先需获得ζ△(x,y)。大量实践证明,二次曲面模型在GPS高程拟合过程中为较优的模型[7],因此通过重力场模型移去高程异常的低频部分后,ζ△(x,y)可以通过以下几种模型获得。

①当测区为带状、东西走向时,则采用数学模型:

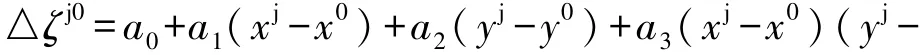
②当测区为带状、南北走向时,则采用数学模型:

③其他情况,则采用数学模型:

式中j表示GPS/水准点；ai(i=0,1,2,…,5)为待求的6个参数；(x0,y0)为区域中心。

3 计算过程

基于以上理论研究,下面给出GPS长距离高程传递过程。

首先,由基准高程点和观测点的GPS水准点,结合式(5)、(3)分别计算ζGM和ζ△；

其次,根据测区的走向,选择式(12)～式(14)拟合残余面；

然后,根据式(10)、(11)计算角度偏差在基准高程点和观测点基线上的分量；

最后,由式(3)、(6)计算观测点在国家基准下的高程。

长距离GPS高程传递的计算流程如图5所示。

图5 高程传递计算流程

4 实例分析

为检验上述模型的正确性,以某较宽河流为研究对象开展高程传递试验。试验区为带状,面积约为4 000 km2,高程变化约38 m。测区内分布15个GPS水准点,如图6所示。

图6 试验区域及GPS水准点分布

将这15个点按图中的分界线分为两组。右边E805(姚港G1)等7个点为虚拟基准高程点,记为组1；左边靖吕27暗等8个点为虚拟待观测点,记为组2。将2组所有GPS水准点的正常高均加5 m,人为改变组2点正常高程起算面。以E805(姚港G1)等为基准高程起算点,采用本文提出的方法计算各观测点在国家高程基准下的正常高。

首先通过式(5),由EGM96全重力场模型分别计算基准高程点和观测点的ζGM。

之后,由两侧GPS水准点,计算各点的ζ△。因为本实验区域为带状、东西走向,故采用式(12)对残余面进行拟合。再由式(10)、(11)结合两侧的残余面的模型分别计算E805(姚港G1)点与各观测点在其基线上的夹角偏差分量。最后根据式(3)和式(6)计算各观测点在国家高程基准下的正常高。计算结果如表1所示。

同理可获得以其余已知高程点为起算点时各观测点在国家高程基准下的正常高,如表2所示。

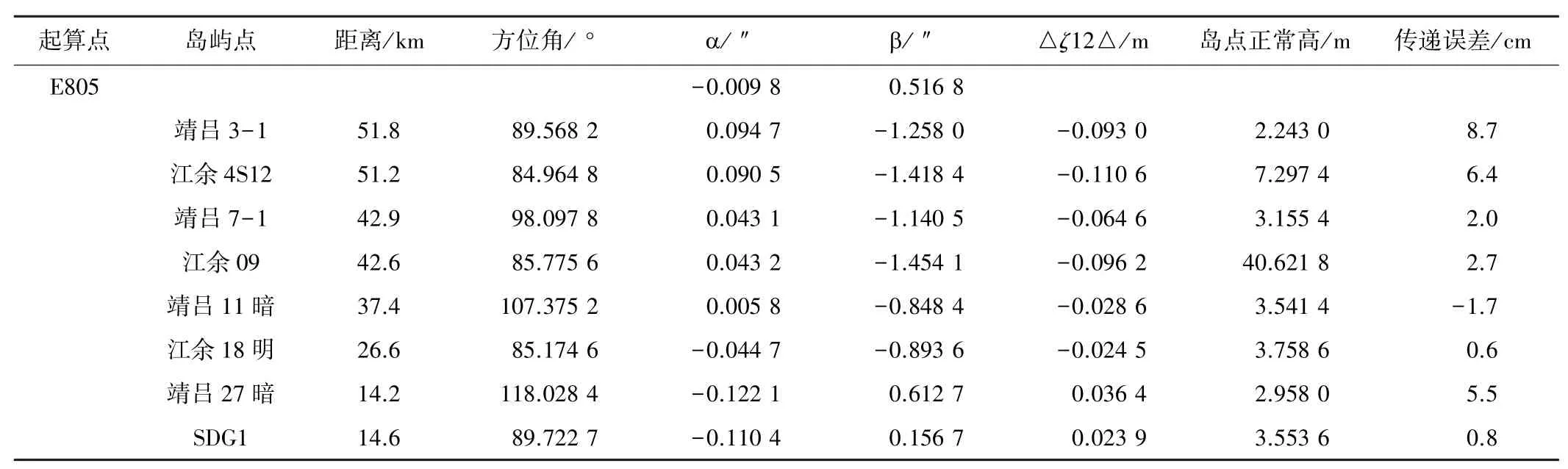
正常高计算表 表1

其余已知高程点作为起算点的计算结果 表2

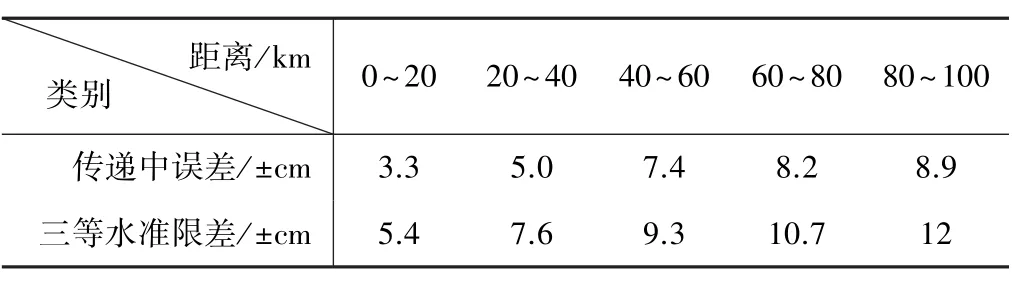
高程传递精度 表3

为检验上述方法的高程传递精度。以20 km为间隔,将100 km分为5组。根据表1、表2中的距离,分别统计各组点数及高程传递误差的均方差,并将各组计算的传递中误差与国家规范中二、三等水准测量的闭合差限差进行比较,比较结果如表3所示。

在表1和表2中,个别点上高程传递的计算结果与实际观测值存在较大偏差,超过了10 cm。究其原因,认为:

(1)测点较少且分布不均匀,通过多项式拟合法计算残余面时,必然会引入模型误差；此外,由于地形因素对高程异常短波部分的影响,增加了精确获取残余面模型的难度。

(2)传递误差与两计算点的分布有关,虽然影响较小,但仍随方位角不同而变化。这种现象当两点间的距离较长时,尤为明显。

(3)角度偏差在基准高程点和观测点方向上的分量的函数与实际情况不符,从而由式(10)计算的结果将存在误差。为此,当距离较长时,可以在已知点区域和观测点区域间增加加密点,然后,根据这些点上的角度偏差分量,拟合两个区域方向上垂涎偏差分量的函数。

(4)所采用的水准测量的成果本身精度不高。

尽管如此,该方法仍然在跨度100 km范围实现了优于三等水准测量的高程传递精度。

5 结 论

本文提出的长距离高程基准传递新方法通过重力场模型移去高程异常的低频部分,使高程异常的剩余部分趋于平缓,然后通拟合法获取残余面形状并计算基准高程点和观测点之间的剩余高程异常差,最后获取两点间的正常高差,进而实现高程的传递。该方法理论严密,简单实用,且无需重力测量,成本低,能较快地实现长距离高程基准传递,满足跨河、跨海,甚至异地高程模型统一的要求,为GPS远距离高程传递提供了一种新的解决方案。

[1] 李建成，姜卫平.长距离跨海高程基准传递方法的研究[J].武汉大学学报·信息科学版，2001(6)：25～32.

[2] 李凤斌，柳光魁，王晓丽等.长距离跨海高程基准传递方法及精度.现代测绘[J].2007，30(2)：6～8.

[3] 周世健，鲁铁定.有限元法拟合GPS水准高程分析[J].江西科学，2007，25(5)：548～552.

[4] 孔祥元，郭际明，刘宗泉.大地测量学基础[M].武汉：武汉大学出版社，2010.

[5] 何万平，楼立志.基于移去-恢复技术的区域似大地水准面拟合方法的研究[J].全球定位系统，2009，17(4)：66～80.

[6] 许曦，刘庆元，朱建军.天文GPS水准方法的研究[J].中南大学学报·自然科学版，2004，35(4)：33～65.

[7] 刘帅，王礼江，朱建军等.GPS高程拟合模型的优选[J].测绘工程，2006，15(4)：17～19.

[8] L VÖLGYESI.Local Geoid Determination Based On Gravity Gradients.Acta Geod，Geoph.，2001，36(2)：153～162.

[9] 李飞.完全规格化缔合勒让德函数算法研究[J].科技风，2010(19)：312～314.

Research on Height Transferring w ith GPS in Long Distance App lications

Cheng Guohui1,2,Tan Qifeng2
(1.School of Geosciences and Info-Physics,Central South University,Changsha 410083,China；2.Changsha City Planning Survey Design Research Institute,Changsha 410007,China)

Based on the“remove-restore”principle,with the aid of GPS astronomical leveling theory,this paper proposed amethod to transfer the height.By themeans of gravity field model,the low-frequency part of anomaly can be removed,and a residual surface of Geoid can be obtained.With the quadratic surface fitting,we can obtain the Geoid residual surface shape and the angle deviation,and calculate the residual anomaly difference between the datum points and observation points.Finally,to get the normal height difference between the datum points and observation points,based on the same height datum.In this paper,a real tests is given,and showed that themethod close to the accuracy of the third order Leveling.Meanwhile,long distance height transfer,such as across the river,across the sea elevation transfer has some reference value.

remove-restore principle；GPS astronomical levels；height anomaly；deflection of the vertical；normal height difference

1672-8262(2013)06-101-05

P228.3

A

2013—02—06

成国辉(1970—),男,高级工程师,注册测绘师,主要从事测绘技术应用与管理工作。