多种拟合方法在区域似大地水准面精化中的运用

马祥

(芜湖市勘察测绘设计研究院有限责任公司,安徽芜湖 241000)

多种拟合方法在区域似大地水准面精化中的运用

马祥∗

(芜湖市勘察测绘设计研究院有限责任公司,安徽芜湖 241000)

主要介绍了自适应最小二乘配置、薄板样条、BP神经网络、多面函数、移动曲面等重力似大地水准面拟合计算的原理，同时以芜湖市似大地水准面精化为例，重点探讨了利用上述拟合方法所体现的精度和适用条件，并逐一对各种拟合方法计算结果做出比较，最后对如何确定合适的拟合方法做出阐述，并给出有益结论。

似大地水准面精化；拟合；自适应最小二乘配置；薄板样条；BP神经网络；多面函数；移动曲面

1 引 言

为了得到更可靠的区域似大地水准面模型,需要利用GPS水准点进行重力似大地水准面拟合纠正。首先经过格网平均重力异常、模型重力异常、模型似大地水准面、剩余法耶异常、重力似大地水准面等计算步骤,完成区域重力似大地水准面计算,根据残差进行粗差探测与剔除；然后利用测区的GPS水准点成果将区域重力似大地水准面拟合适配于该区域的实测似大地水准面。在移去重力似大地水准面后,选取合理有效的拟合方法成为提高似大地水准面精化精度的关键因素。拟合纠正时,利用GPS水准点上的实测似大地水准面ζGPS与由规则格网内插的重力似大地水准面ζgra的差值△ζ,采用多种拟合方法对区域重力似大地水准进行拟合纠正。常用的拟合方法有自适应最小二乘配置、薄板样条、BP神经网络、多面函数、移动曲面拟合。本文拟从如何选择合适的拟合方法以及适用条件试图做出一些有益探讨。

2 常用的拟合方法

2.1 自适应最小二乘配置法

该方法中观测噪声与信号的方差协方差一般靠经验或函数模型得到,这可能造成二者之间不合理的关系,这些不合理可以部分归结于方差因子的不一致。因此,采用Helmert方差分量估计自适应地调整观测噪声与信号的方差协方差的比例关系,可以提高区域似大地水准面拟合精度。

Helmert方差分量估计的基本思想是通过利用平差计算得到第i个去估计验后单位权中误差,进行迭代计算,合理地调整观测噪声与信号权矩阵的比例,直至二者的比例协调为止。主要步骤:假设信号的协方差函数已拟合,可得到信号、观测噪声的方差-协方差阵、。依文献[7],设自适应最小二乘配置的目标函数为:

假设等精度独立观测,初始单位权方差为1.0,则初次平差的先验权阵分别为:

计算第i次平差得到的改正数,则信号、观测噪声的验后单位权方差为、。

其中:

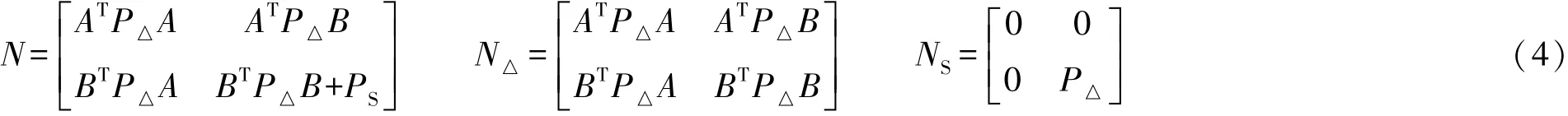
依据方差分量估计计算信号、观测噪声的验后单位权方差,依此重新定权,求解倾向参数和随机信号向量。

2.2 薄板样条函数

薄板样条是一种二维曲面,它是由一维三次样条到二维的扩展。该曲面通过所有控制点且不要求拟合点呈规则格网排列,在认为实际高程异常是连续渐变时,由于样条函数是曲率最小光滑的曲面,每个拟合点(控制点)可控制局部范围,该方法具有离拟合点越远相关性越小的特点。

薄板样条拟合法是基于无限大平板小挠度方程的数学模型,其函数模型如下:

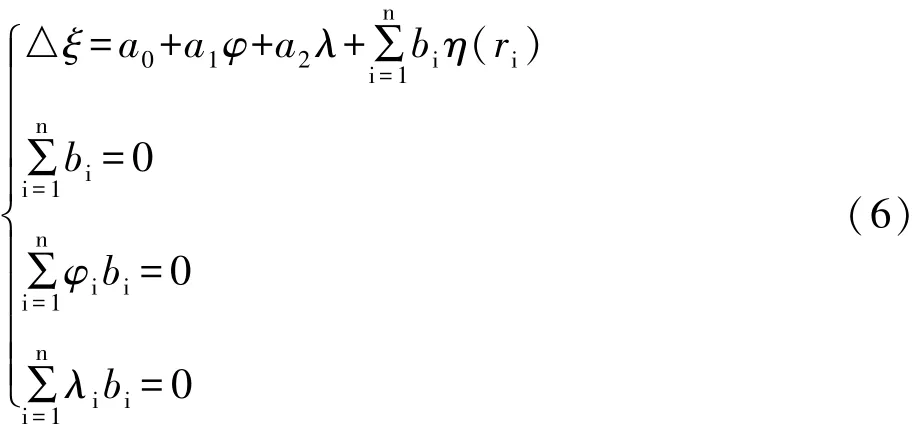
2.3 BP神经网络函数

BP神经网络是一种多层前向神经网络,由于学习算法采用BP算法而称之为BP神经网络。神经网络通过大量学习样本训练网络,能以任意精度逼近连续函数；神经网络可以处理含有不确定因素影响的问题,该方法不需要知道变量与函数值之间的具体函数表达,它是一种复杂的非线性映射系统,可以削弱无法模型化的系统误差以及剩余误差等影响,提高神经网络的计算精度；神经网络函数模型简单,原理为误差最小估计准则。

该算法采用数据正向传播、误差反向调节的方法,提高样本训练精度和泛化能力。其计算过程如下:

设选取拟合点与检核点的纬度与经度作为神经网络输入向量,则第i个样本的输入向量为Xi=[φi, λi]；第i个样本的期望输出为该点的GPS水准似大地水准面与重力似大地水准面之差,即di=△ζi；输入层与隐含层的权为w,维数为n×s；阈值为θ1,维数为s× 1；隐含层与输出层的权为w′,维数为s×m；阈值为θ2,维数为m×1；n、s和m分别为输入层、隐含层和输出层

式中,的神经元节点数。在拟合计算中,n和m分别取2、1；隐含层s一般依靠经验取值,此处s的数值为25。

神经网络的正向传输的计算过程为:

隐含层的输出:

其中,(I′l)p=∑sj=1w′j(z)p

j-(θ2)l。

所有训练样本的误差平方和E为:

其中,dpl为期望输出d的第p个样本的第l个元

无论是函数模型拟合、统计模型拟合还是两类模型的组合拟合都需要知道明确的模型表达式,这对一些不能模型化因素以及非线性化强度较大问题的计算都存在一定难度。而神经网络特别适合处理需要同时考虑许多因素和条件的、不精确的模糊信息,理论证明具有单隐含层的网络结构能够以任意精度逼近连续函数。

2.4 多面函数

多面函数是用一系列有规则的数学表面以任意精度逼近一个光滑的数学表面。多面函数的核心是核函数的选择和节点与平滑因子的确定。实际应用中,多面函数参数选取与核函数、数据点个数和分布等因素有关,因此应根据具体情况选取核函数等参数。

设地面上的任一点属性值可由S个核函数g(x, y,x0,y0)的总和去逼近,即:素；N为输入样本的总数。

神经网络的误差反向调节过程为:

隐含层与输出层之间的连接权调整公式:

式中,z(x,y)为点(x,y)的地理属性值,g(x,y,x0, y0)为核函数。原则上讲,核函数可任意选用,但为了简单,常假定核函数是对称的,可取圆锥面

其中,(x0,y0)为节点,可直接采用已测数据点,或已测数据点的统计值,δ为平滑因子,用来调整核函数的形状,β≫k(k=1,2,.…s)为待定系数,α为曲面类型常取为0.5或-0.5。

2.5 移动曲面

移动曲面法以每个待估点为中心,选取周围的数据点按其贡献的大小参与拟合并考虑这些点的分布及地形起伏的影响。因此,在高程异常变化复杂的区域,以向径的某一函数作为权函数,采用移动曲面法更好地发挥拟合点的作用,加强对异常趋势的拟合,从而拟合曲面更真实反映高程异常的趋势。

对于曲面的选择,一般采用二次曲面作为拟合曲面:

其中权P的确定原则:按照待定点与数据点的距离ρ关系,ρ越大权越小,ρ越小权越大。对于不同地形起伏条件,权函数的选择可根据实际情况采用,建议权函数的选择采用如下两种权函数:

其中,ρi为待定点到数据点的距离；k是一个常数,一般取平均距离的2倍。

3 实例计算与分析

以芜湖市似大地水准面精化为例,共布设了52个GPS水准点(包括15个外部检核点),搜集周边地区18个GPS水准点。首先使用70个GPS水准数据作为拟合数据,并采用最小二乘配置方法进行计算。分析拟合点残差,未发现粗差点。并经多次计算,发现纠正积分半径为35 km的重力似大地水准面的计算效果最好。最终利用芜湖市均匀布设的37个GPS水准点,收集周边地区的18个GPS水准点,共计55个点,用于芜湖市似大地水准面的拟合,并且利用芜湖市均匀布设的15个外部检核点作为芜湖市似大地水准面的检测。点位分布情况如图1所示:

图1 GPS水准点(拟合点、外部检核点)分布图

3.1 拟合纠正方法及精度

分别采用自适应最小二乘配置、薄板样条、BP神经网络、多面函数与移动曲面等拟合方法,利用GPS水准点对重力似大地水准面模型进行拟合纠正,利用GPS水准点的似大地水准面ζGPS与由规则格网内插的最终似大地水准面ζgrid的残差值△ζ来进行似大地水准面精度统计。在最小二乘配置计算时,使用二次多项式逼近数据中的趋势项部分,选取似高斯函数作为信号的协方差函数模型；为了使观测噪声与信号的协方差相一致,利用Helmert方差分量估计调整二者的比例关系,进而提高似大地水准面的拟合效果。在薄板样条函数拟合曲面时,选取全部已知拟合点为结点,即方程个数为n+3个,未知参数个数亦为n+3个,因此,各拟合点的改正量为0；平滑因子在0.000 1～0.1之间自动选取。BP神经网络拟合时,输入向量为某点的纬度与经度,期望输出为对应点的△ζ,因此,神经网络的输入层节点与输出层节点分别为2、1；选取55个点作为训练样本,15个点为检测样本；学习效率η为0.1；计算最大次数为50 000；训练精度为0.001 5；移动曲面权函数采用距离的倒数；多面函数的核函数采用圆锥函数。各种方案误差统计如表1所示；误差曲线如图2～图6所示。

利用多种方法拟合误差统计结果 表1

3.2 结果分析

(1)采用自适应最小二乘配置,是在最小二乘配置拟合的基础上,利用Helmert方差分量调整观测噪声与信号的协方差之间的比例,使二者对拟合结果的贡献更加符合真实情况,其内符合精度都达到±1.1 cm,外部检核精度达到了±1.3 cm。

(2)采用薄板样条函数,以全部拟合点为节点,充分利用各拟合点的已知信息,将拟合点作为无误差的观测量,内符合残差为0.0 cm,外部检核精度达到了±1.3 cm。

图2 自适应最小二乘配置拟合点和检核点残差图(左图为拟合点残差图)

图3 多面函数拟合点和检核点残差图(左图为拟合点残差图)

图4 移动曲面检核点残差图 图5 薄板样条函数检核点残差图

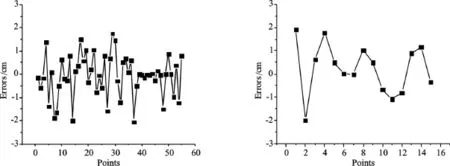
图6 BP神经网络拟合和检核点点残差图(左图为拟合点残差图)

(3)采用BP神经网络逼近区域似大地水准面,削弱数据中的系统误差等因素影响,得到了内符合精度±0.9 cm、外部检核精度达到了±1.1 cm的计算结果。(4)利用移动曲面拟合区域似大地水准面,实现了内符合残差为0.0 cm,外部检核精度达到了±1.2 cm。

(5)多面函数选取圆锥面逼近区域似大地水准面,实现了内符合精度±1.2 cm,外部检核精度达到了±1.4 cm。

3.3 选择合适的拟合方法

同时还采用了多项式、球冠谐函数、最小二乘配置等拟合方法进行了计算,过程在此略过,计算结果表明,多项式内符合精度±1.3 cm,外部检核精度±1.3 cm；球冠谐函数内符合精度±1.3 cm,外部检核精度±1.2 cm；最小二乘配置内符合精度±1.1 cm,外部检核精度±1.3 cm；总体与以上几种拟合法得出的结果很接近。

为了比较各种方案符合性,将基于自适应最小二乘配置的计算结果作为参考值,其他方案结果与参考值比较,差值如图7所示(CO代表自适应最小二乘配置,SP代表薄板样条,BP代表BP神经网络,MS代表移动曲面,HMS表示多面函数)。

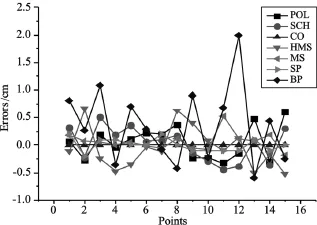
图7 各方案检核点互差图

由图7可知:各种方案的检核点成果与基于自适应最小二乘配置的成果符合性都较好。但是自适应最小二乘配置方法利用Helmert方差分量调整观测噪声与信号的协方差之间的比例,使二者对拟合结果的贡献更加符合真实情况,经过多次验算,自适应最小二乘配置的成果较为稳定,所以最终选择自适应最小二乘配置法作为芜湖市似大地水准面的拟合方法。

4 结 论

(1)自适应最小二乘配置拟合方法达到的内、外部检核精度不是最好,但是自适应最小二乘配置在一定程度上能够提高拟合效果,使似大地水准面更接近于真实值。

(2)采用BP神经网络拟合效果优于其他拟合方法,但是该方法的计算结果随机性强,网络隐含层的层数及单元数的选择具有不确定性,多次计算得出的结论并不统一,且外推能力不强,因此最终没有采用。

(3)最小二乘配置、薄板样条、多面函数、移动曲面以及多项式、球冠谐函数等拟合方法可根据需要和现有适时选择,在精化要求不是非常高的情况下,均能达到较为理想的精化效果。

[1] 芜湖市勘测院.芜湖市似大地水准面精化技术总结报告[R].

[2] 郭春喜，伍寿兵，王惠民等.区域厘米级大地水准面的确定[J].测绘通报，2000，9：3～4.

[3] 杨小青，胡伍生.基于神经网络的似大地水准面模型精化方法研究[J].测绘工程，2008，4：8～11.

[4] 郭春喜，聂建亮，王斌等.利用自适应最小二乘配置的GPS水准与重力似大地水准面的拟合[J].武汉大学学报·信息科学版，2013，1.

[5] 李慧，王洪峰.秦皇岛市似大地水准面精化分析研究[J].城市勘测，2010，6(Z1)：76～78.

[6] 杨庆振，郭春喜.多种拟合方法在似大地水准面精化中的比较[J].测绘标准化，2009，1：30～32.

[7] 杨元喜，曾安敏.顾及几何观测信息和地球物理模型的形变参数自适应滤波解[J].中国科学(D辑)，2009，39 (4)：437～442.

App lication of various Fitting M ethods in Regional Geoid Refinement

Ma Xiang
(Wuhu Geotechnical and Survey Design Institute Co.,Ltd.Wuhu 241000,China)

The papermainly introduces principle ofmobile surface gravity geoid fitting calculation,such as the adaptive least squares collocation,thin plate spline,the BP neural network,polyhedral function,at the same time takingWuhu city geoid refine as an example,discussed precision and applicable condition of the use of the fittingmethod,and one by one compare various fittingmethod calculation results,finally gives a brief description of the fittingmethod of how to determine the appropriate and useful conclusions.

regional geoid refinement；fitting；adaptive least squares collocation；thin plate spline；BP neural network；themultisurface function；moving surface

1672-8262(2013)06-96-05

P228

A

2013—03—22

马祥(1979—),男,高级工程师,注册测绘师,注册监理师,主要从事城市测量技术工作。

住房和城乡建设部科学技术计划项目示范工程(2012-KJA-203)