限位装置对桩基础高墩摇摆反应的影响
2013-03-05夏修身陈兴冲
夏修身,陈兴冲
(1.同济大学 土木工程学院,上海200092;2.兰州交通大学 土木工程学院,甘肃 兰州730070)
基于基础隔震的设计理念[1-5],铁路高墩桥梁的桥墩与桩基础在承台中上部采用分离设计,利用竖向荷载来抵抗引起倾覆的水平荷载能够满足正常使用的要求,强震作用下当桥墩的地震弯矩超过其抗倾覆弯矩时,桥墩发生提离摇摆,提离摇摆后的最大墩底弯矩基本保持不变,承台底的地震作用将大幅度减小,且受输入地震动强度及其频谱特性的影响较小[6].摇摆隔震桥墩中不会再产生塑性铰区,可以确保震后结构的完整性,能节省巨额的塑性铰区修复费用[7-8].
高墩桥梁摇摆隔震效果好且稳定,但摇摆隔震会显著增大墩顶位移,限位装置可以减少墩顶位移,但其对高墩摇摆的反应有何影响缺乏研究.国内外对限位装置的研究主要侧重于抗震桥梁的防落梁及防碰撞[9-12].
本文提出考虑限位的桩基础高墩摇摆隔震分析模型,研究限位装置的初始间隙及其屈服力对高墩摇摆反应的影响.
1 桩基础高墩的摇摆隔震装置
文献[6]提出了桩基础高墩摇摆隔震装置(见图1),强震下通过提离摇摆能达到既保护桥墩又保护基础的抗震目标.
桥墩在正常使用及多遇地震作用下的水平力由桥跨重及桥墩自重共同抵抗,按岩石地基上的扩大基础进行抗震设计.在设计或罕遇地震下,桥墩相对于桩基础将发生摇摆,摇摆过程中通过钢筋或钢铰线限制墩顶的位移.
2 桩基础高墩摇摆隔震分析模型
图1所示的桩基础高墩摇摆隔震装置桥墩在承台上提离摇摆,墩底扩大基础本身的变形很小,承台接近刚性.基于这样的提离摇摆特点,当不考虑限位钢筋时,本文提出用2个大刚度竖向弹簧模拟强震下铁路桩基础高墩的提离摇摆(见图2a),此模型记作模型I.

图1 高墩基础摇摆隔震装置Fig.1 Tall pier using controlled rocking approach
两弹簧模型中以弹性梁单元模拟墩柱,集中质量模拟桥跨重,刚臂单元模拟墩底扩大基础,基础质量堆积于扩大基础的重心.墩底扩大基础每端各设置1个只受压的提离弹簧模拟桥墩摇摆,提离弹簧的力-位移关系示于图2b.弹簧的受压刚度k取较大值,本文建议在108~1011kN·m-1之间.模型采用瑞利阻尼,C=αM+βK,其中C,M与K分别为阻尼矩阵、质量矩阵与刚度矩阵,α,β为系数,计算时各阶振型采用相同的阻尼比.

图2 不考虑限位的两弹簧模型Fig.2 Two spring model without restrainer element
摇摆高墩扩大基础的竖向提离超过限位装置(限位钢筋与初始间隙的总称)的初始间隙时,限位钢筋会对摇摆高墩产生约束作用.考虑限位的摇摆隔震分析模型见图3,此模型记作模型II.模型II中阻尼、墩柱、梁与基础、提离弹簧的模拟与模型I完全相同.限位装置中的限位钢铰线或钢筋采用只受拉不受压的非线性单元模拟,考虑间隙的只受拉不受压非线性单元的力-位移关系示于图3a.图中δ,Fy分别为限位装置的初始间隙及限位钢筋的屈服力;A,B,C,D为限位单元的加、卸载路径控制点;①~⑦为限位单元的加、卸载路径.
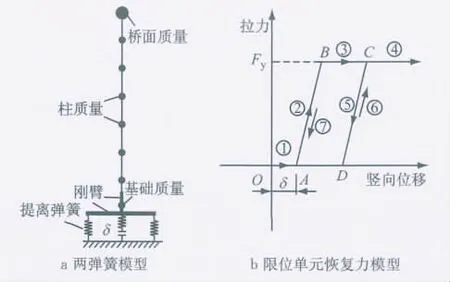
图3 考虑限位的两弹簧模型Fig.3 Two spring model with restrainer element
图3b中限位单元屈服前刚度kAB按下式计算:

式中:E为限位钢筋或钢铰线的弹性模量;A为限位钢筋或钢铰线的截面积;L为限位钢筋或钢铰线的非约束长度.
限位单元的滞回规则由3条加、卸载路径组成,如下:
(1)①→②→③→④为从点O至点C及其以后的持续加载路径.
(2)③→⑤→⑥为从点C卸载至点D,再从点D(或D到C之间的任一点)加载至点C的路径.
(3)②→⑦为从点A(或A到B之间的任一点)加载至点B,再从点B(或A,B之间的任一点)卸载至点A的路径.
3 摇摆隔震分析模型比较
为表明本文提出的两弹簧分析模型可以较好地模拟桩基础高墩的摇摆反应,本文模型与文献[6]中分析模型进行了结果比较.
3.1 基本数据
某单线铁路特大桥上部结构为等跨布置32m简支箱形梁,下部结构为圆端形空心高墩、群桩基础,桥型立面布置示于图4.以58m高的18号桥墩为摇摆隔震研究对象,隔震前18号墩顺桥向的第1周期为0.95s.以El-centro强震记录作为输入地震动,为考察摇摆反应的离散性,还输入了Taft与Northridge地震波,3条地震波的幅值统一调整为0.57g.

图4 某铁路高墩桥梁的立面布置(单位:m)Fig.4 Elevation of a typical tall pier railway bridge(unit:m)
3.2 2个模型结果的比较
两弹簧模型中提离弹簧刚度取较大值,本文取1.0×1011kN·m-1.图5、图6及表1是本文的两弹簧模型与文献[6]中转动弹簧模型的高墩摇摆反应比较,分析中2个模型均没有考虑限位装置的影响.
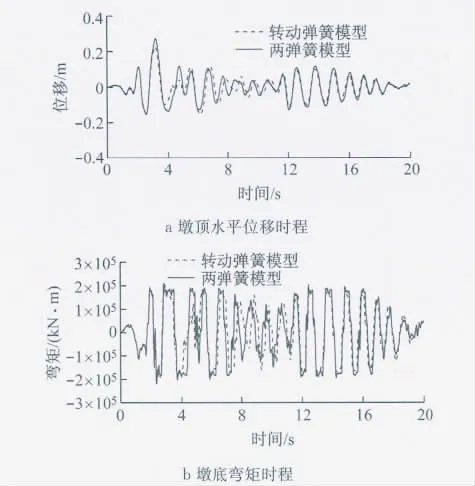
图5 墩顶水平位移与墩底弯矩时程曲线(El-centro波)Fig.5 Comparison of displacement at pier top and moment of pier base(EI-centro Wave)
由图5可以看出,本文提出的两弹簧模型与文献[6]中转动弹簧模型的墩顶位移、墩底弯矩时程曲线吻合较好.由图6可以看出,2个模型的弯矩-转角关系曲线有一定的差异,这主要是转动弹簧模型计算时输入弹簧的弯矩-转角恢复力曲线有一定的近似,其不能反映竖向力变化的影响,但总体来看2个模型的结果吻合较好.

图6 弯矩-转角关系(El-centro波)Fig.6 Comparison of moment-rotation hysteretic curve(EI-centro Wave)
由表1可以看出,摇摆隔震的墩顶位移受输入地震动的影响很大,同等地震强度下Northridge的墩顶位移是Taft波的3倍多,是El-centro波的2倍多.摇摆隔震显著增大了墩顶位移,需要采取相应的限位措施.

表1 摇摆隔震分析模型比较Tab.1 Comparison of the results of two models for rocking isolation
4 考虑限位装置的桩基础高墩摇摆隔震分析
为讨论限位装置对摇摆高墩地震反应的影响,对图4所示的18号高墩进行限位设计.在承台中心附近布置20根φ32的精轧螺纹钢进行限位.限位钢筋的屈服力Fy=14 951kN,取δ=20mm.考虑限位及不考虑限位影响的摇摆隔震分析结果示于图7及表2.
由表2可以看出,在El-centro及Taft波下,摇摆中扩大基础的提离未超过初始间隙δ=20mm,此时限位钢筋不起作用,模型II与模型I的结果相同.

图7 考虑与不考虑限位影响的结果(Northridge波)Fig.7 Seismic response with restrainer or without restrainer(Northridge Wave)

表2 摇摆隔震反应比较Tab.2 Comparison of the seismic response of two models for rocking isolation
由图7a、图7b及表2可以看出,在Northridge波下,限位钢筋对摇摆高墩产生约束作用,墩顶最大水平位移由原来518mm减小到469mm,减小了9.5%,但墩底弯矩增大了17.5%.这表明限位装置在减小墩顶位移的同时增大墩底弯矩.
由图7c、图7d可知,基础中心的竖向位移时程曲线及弯矩-转角关系也发生了较大的改变,这表明限位装置减少了基础的提离次数.
为深入了解限位装置对高墩摇摆反应的影响,进行了Northridge波作用下δ及Fy的参数分析,每次只改变其中一个参数.Fy=14 951kN不变、δ由∞→0的分析结果见图8及表3.表中及图中Fy=0及δ→∞均表示不考虑限位装置的影响.

图8 不同初始间隙下的弯矩比较(Northridge波)Fig.8 Comparison of moments for variousδ(Northridge Wave)

表3 不同初始间隙的摇摆反应比较Tab.3 Rocking response of variousδ
由图8及表3可知,Fy不变,δ由∞→0时,设置限位钢筋可以减小墩顶水平位移,也会增大墩底弯矩.
由表3可以看出,屈服力Fy不变,当δ由∞减小至20mm时,墩顶最大水平位移减小了9.5%,而墩底弯矩的峰值增大了17.5%.而当δ由20mm减小至零时,墩顶最大水平位移减小了23%,但墩底弯矩峰值仅变化了2.8%.这表明,墩顶位移随限位装置初始间隙的减小而减小,受限位装置初始间隙的影响较大;限位钢筋起约束作用后墩底弯矩受δ的影响相对较小.
由表3可见,在Northridge波下当δ由20mm减小至10mm时墩底弯矩峰值还出现了减小的现象,图8c可以解释这一现象.图8c中的a,b与c为4个δ值对应曲线的分离点.在点a对应的时刻之前4个曲线完全重合,表明桥墩没有发生提离,限位均不起作用.点a之后,δ=0的限位产生作用,由于限位钢筋的影响其弯矩较其他3个有所增大.点b与c分别对应δ=20mm和δ=10mm的起始限位时刻,限位之后的弯矩均较无限位(δ=∞)的弯矩有所增大.由于发生限位的时刻不同,相同屈服力下的墩底弯矩时程曲线形状相近,但弯矩峰值出现在不同时刻(对应不同的地震波强度),所以δ=20mm减小到δ=10mm时墩底弯矩峰值出现了减小的现象也很好理解.
δ=20mm不变、Fy由0→20 000kN的分析结果见图9及表4.

图9不同屈服力下的位移与弯矩比较(Northridge波)Fig.9 Comparison of displacements and moments for various Fy
从图9及表4可以发现,δ不变,Fy由0→20 000kN时,墩顶最大水平位移随屈服力的增大而减小,墩底最大弯矩随屈服力的增大而增大.墩顶位移及墩底弯矩受Fy的影响相对较大,这是因为限位钢筋的屈服力与桥墩提离弯矩My(见式(2)及表5,表中M2为限位装置提供的弯矩,ME为地震反应弯矩,My=M1+M2,ρ=(ME-My)/My)有相关性.因此屈服力增大,提离后的墩底弯矩也会增大.限位钢筋屈服力的提高不仅能降低桥墩提离幅度(图10),还会在一定程度上增大塑性耗能(图11),故墩顶位移也会随之减小.

表4 不同屈服力的摇摆反应比较Tab.4 Rocking response of various Fy
提离弯矩(抗倾覆弯矩)的简化计算公式[6]为
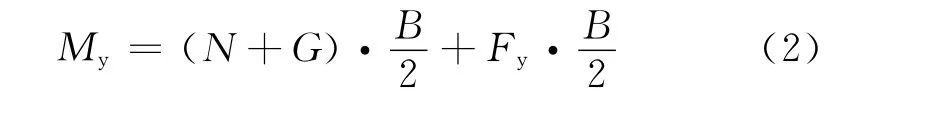
式中:N为墩顶的支反力;G为墩身的自重;B为与墩身相联的计算方向扩大基础宽度.
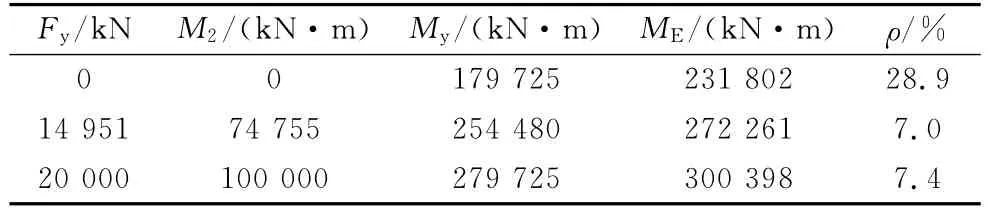
表5 地震反应弯矩与提离弯矩比较Tab.5 Comparison of seismic moments and lift-off moments

表5是B为10m、恒载为35 945kN,恒载提供的弯矩M1为179 725kN·m时的不同屈服力下桥墩地震弯矩与提离弯矩的比较.由表5也可以看出,提离后墩底的ME大于My(这是由于桥墩本身的动力效应引起),并且与提离弯矩有相关性.
5 结论
(1)提出了限位装置的模拟方法,完善了桩基础高墩摇摆隔震的分析模型.
(2)限位装置减少桩基础高墩的摇摆提离次数,在减小墩顶位移的同时增大墩底弯矩.
(3)墩顶位移随限位装置初始间隙的减小而减小,受限位装置初始间隙的影响较大;墩底弯矩受初始间隙的影响较小,设计中可不计其影响.
(4)限位装置屈服力对桩基础高墩摇摆反应的影响较大,墩顶位移随屈服力的增大而减小,墩底弯矩随屈服力的增大而增大,设计中需要考虑其对摇摆反应的影响.
[1] Panagiotis Elia Mergos,Kazuhiko Kawashima.Rocking isolation of a typical bridge pier on spread foundation [J].Journal of Earthquake Engineering,2005,9(2):395.
[2] Alessandro P,Stefano P,Gian M C.Concept and development of hybrid solutions for seismic resistant bridge systems[J].Journal of Earthquake Engineering,2005,9(6):899.
[3] 王荣辉,曾庆元,舒文超.钢球-限位系统隔离桥梁结构水平地震作用的试验及分析[J].实验力学,1999,14(1):19.WANG Ronghui,ZENG Qingyuan,SHU Wenchao.An earthquake isolation system for bridge piers[J].Journal of Experimental Mechanics,1999,14(1):19.
[4] CHEN Yihsuan,LIAO Weihsin,LEE Chienliang,et al.Seismic isolation of viaduct piers by means of a rocking mechanism[J].Earthquake Engineering and Structural Dynamics,2006,35:713.
[5] Alain Pierre.Design and construction of the Rion Antirion bridge[J].Geotechnical and Engineering for Transportation Projects,2004,216.
[6] 夏修身,陈兴冲.铁路高墩桥梁基底转动隔震与墩顶减震的效果对比研究[J].铁道学报,2011,33(9):102.XIA Xiushen,CHEN Xingchong.Controlled rocking and pier top seismic isolation of railway bridge with tall piers[J].Journal of the China Railway Society,2011,33(9):102.
[7] 洪晓慧,葛伊仁,刘光晏,等.考虑直接基础摇摆机制之桥梁耐震性能研究(III)[R].台湾:地震工程研究中心,2010.HUNG Hsiaohui,GE Ireng,LIU Kuangyen,et al.Seismic performance of bridge with rocking spread footing[R].Taiwan:Center for Research on Earthquake Engineering,2010.
[8] Saiidi M,Randall M,Maragakis E,et al.Seismic restrainer design methods for simply supported bridges[J].Journal of Bridge Engineering,2001,6(5):307.
[9] Trochalakis P,Eberhard M O,Stanton J F.Design of seismic restrainers for in-span hinges [J]. Journal of Structural Engineering,1997,123(4):469.
[10] 王军文,李建中,范立础.桥梁中抗震限位装置设计方法的研究[J].土木工程学,2006,39(11):90.WANG Junwen,LI Jianzhong,FAN Lichu.A study on the design method of seismic restrainers for bridges[J].China Civil Engineering Journal,2006,39(11):90.
[11] 戴福洪,翟桐.桥梁限位器抗震设计方法研究[J].地震工程与工程振动,2002,22(2):73.DAI Fuhong,ZHAI Tong.Study on aseismic design method of restrainers for highway bridge[J].Earthquake Engineering and Engineering Vibration,2002,22(2):73.
[12] 高玉峰,蒲黔辉,李晓斌.梁式桥地震碰撞响应及防碰撞与落梁措施研究进展[J].地震工程与工程振动,2011,31(1):80.GAO Yufeng,PU Qianhui,LI Xiaobin.State-of-arts of earthquake-induced pounding responses of girder bridges and measures for preventing pounding and span collapse[J].Journal of Earthquake Engineering and Engineering Vibration,2011,31(1):80.
