煤矿配电网故障定位研究

王建亮

（山西焦煤西山煤电集团公司，山西 太原 030053）

·试验研究·

煤矿配电网故障定位研究

王建亮

（山西焦煤西山煤电集团公司，山西 太原 030053）

传统的单端行波测距方法无法有效识别特殊波头，由于受零模波速不稳定的影响，导致基于模量波速差的行波测距结果误差较大。本文对上述问题提出改进，分析得到随着传输距离的增加，零模检测波速单调递减，而两模量传输时差则单调递增，故考虑基于BP神经网络的训练学习对零模波速进行估算，而后再利用模量波速差进行故障测距，仿真表明，该方法对各种故障情况均适用且具有较高的精度。

煤矿电网；单相接地；故障测距；相模变换

配电线路是煤矿电网中发生单相接地故障最多的地方，准确快速地排除故障点使系统快速恢复正常供电。为此故障测距的研究对提高煤矿电网的稳定性和安全性具有十分重要的意义。单端故障测距法较之双端法不需要通信通道和信号同步，从而降低了成本，提高了可靠性。但现有单端法的测量精度没有双端法高，因此，精确的单端故障测距是煤矿供配电安全领域的重要研究方向之一。

无论是单端测距还是双端测距，它们的测量精度都会受到实际线路长度变化和设定行波波速误差的影响。文献［1］根据现有的输电线路双端行波故障测距原理，提出一种与波速无关的双端行波测距方法，但没有考虑双端同步时误差对测距结果的影响。文献［2］利用行波极性来分辨故障点和对端母线反射波，但在母线上有变压器且除故障线路外无其它出线的情况下，母线反射波极性会发生变化，此时该方法无法准确识别故障点反射波；文献［3］根据故障行波电流信号线模分量的模极大值性质，提出一种单端行波测距方法，但其仅仅针对一条线路进行仿真，没有考虑其他健全线路反射波头的影响。

本文是基于行波线模分量和零模分量波速差的单端行波故障测距。首先通过凯伦鲍尔变换将暂态电流行波转换为没有电磁耦合的模分量，并对线模和零模分量波速随信号频率的变化展开分析，得出线模分量波速较稳定，而零模波速具有较强的依频特性。利用BP神经网络的训练和学习，基于在测量端检测到的两模量传输时间差来估算零模波速，从而基于模量波速差进行故障测距。

1 基于模量波速差的单端行波测距

1．1 故障行波模量分析

均匀三相输电线路上任一点的电压和电流满足关系式：

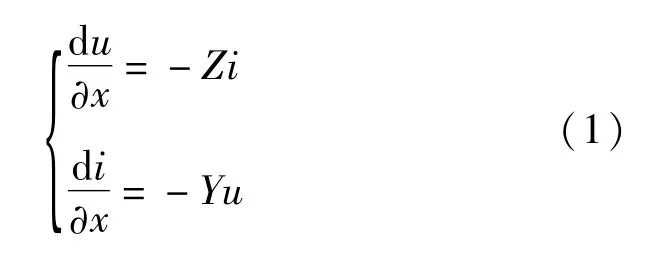
式中：

u—频域中的相电压列向量，u=［uA，uB，uC］T；

i—频域中的相电流列向量，i=［iA，iB，iC］T；

x—线路至测量端的距离；

Z—单位长度线路的串联阻抗矩阵，Z=R+jωL；

Y—单位长度线路的并联导纳矩阵，Y=G+jωC。

式（1）可改写为：

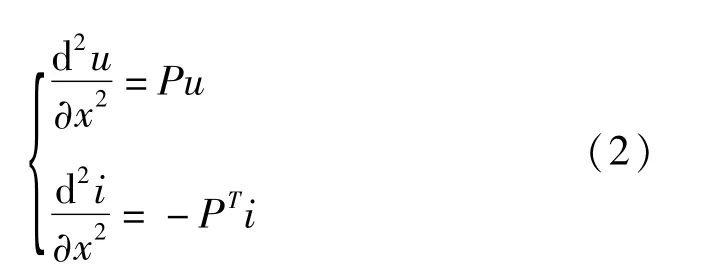
式中：P=ZY，PT=YZ，式（2）即为三相线路在频域的波动方程组，由于三相线路各相间存在电磁耦合，每一相的波动方程均不是独立的，一般通过相模变换来解除耦合［4-5］。对于故障线路，P为非对角阵，由于P为非奇异阵，故总能找到变换矩阵S使T =S-1，PS为对角阵，如此得到三相线路在频域的模分量波动方程组：

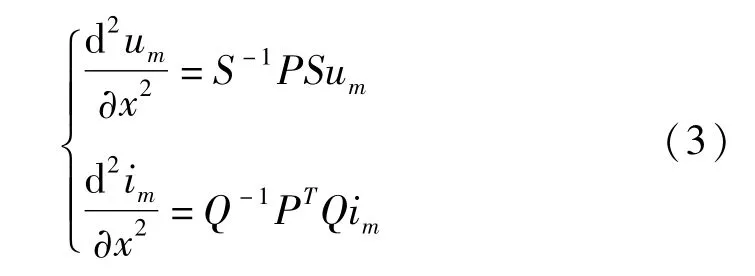
式中：im=［i（0），i（1），i（2）］=Q-1［iA，iB，iC］，um=［u（0），u（1），u（2）］T=S-1［uA，uB，uC］T。

Q和S是同类型的变换矩阵，um和im为模量，u（0）、i（0）是零模分量，u（1）、i（1）和u（2）、i（2）是线模分量。相模变换和反变换的公式为：

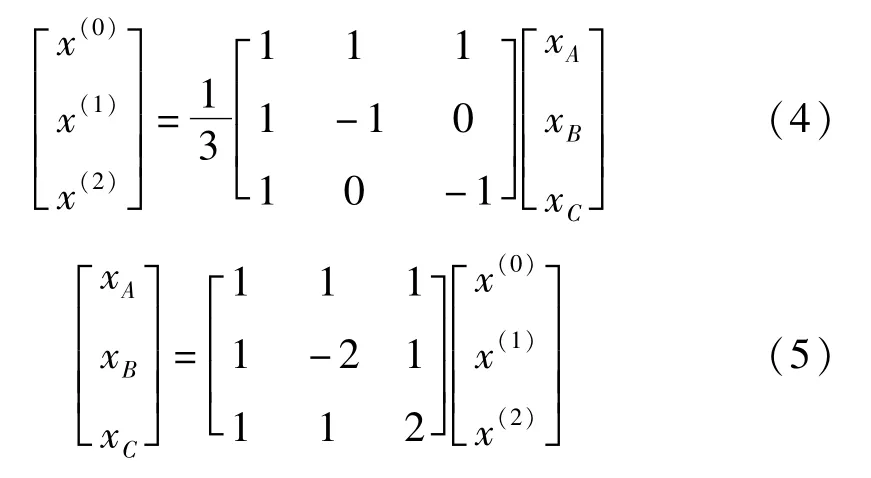
式中：x（1）、x（2）为电流或电压行波的线模分量，x（0）为零模分量。三相行波的零模、α模与β模分量含义见图1。

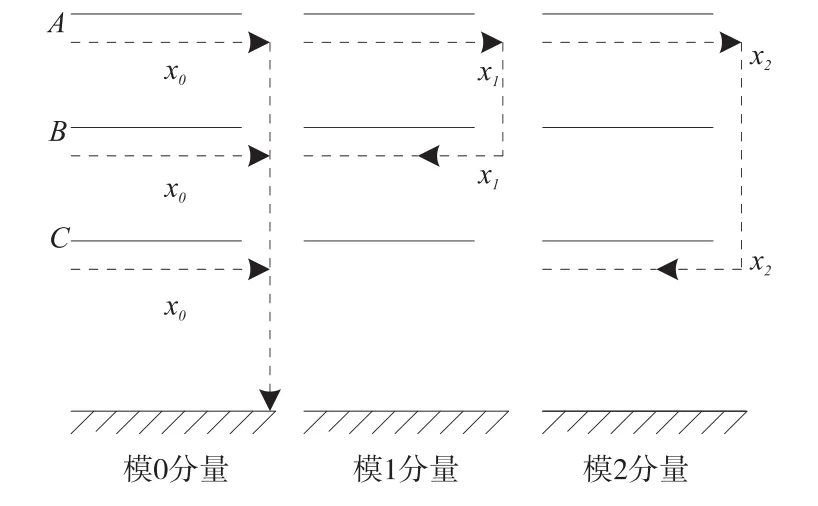
图1 行波模分量在三相线路上的分布示意图

1．2 基于模量波速差的测距原理

电力线路发生单相接地故障时，暂态行波信号可分为行波零模分量和行波线模分量，两分量的波速是不同的，两者达到母线测量端的时刻也不一样，根据这些信息便能够求出故障点到母线测量端之间的距离，具体原理如下：

假定v1为行波线模分量波速，v0为零模分量波速，线模分量到达测量端M的时刻为T1，零模分量到达测量端M的时刻为T2，见图2。

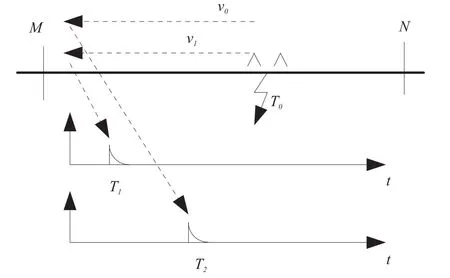
图2 行波传输时差故障测距原理图

则可计算得故障点到测量端的距离X为：

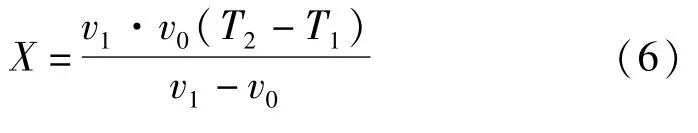
此方法的关键是提取出行波零模分量和线模分量的波头到达时刻，可以通过小波变换进行分析，设定合适的窗函数，找出波头的准确时间。

利用模量波速差进行故障测距时，仅利用故障发生后初始行波到达测量端的数据信息，不用区分故障点的反射波和线路末端的反射波。此方法的弊端是线路比较短时，时差T2-T1小，检测难度较大；故障点距离测量端越近时，误差越大，甚至无法检测出时差。因此，必须采用高速数据采集卡来减少测量误差。

2 模量波速分析及零模波速估算

2．1 模量波速分析

本文中仿真线路均采用依频变化的分布参数线路模型。此模型下，模波阻抗和模行波分量的传播系数分别为：

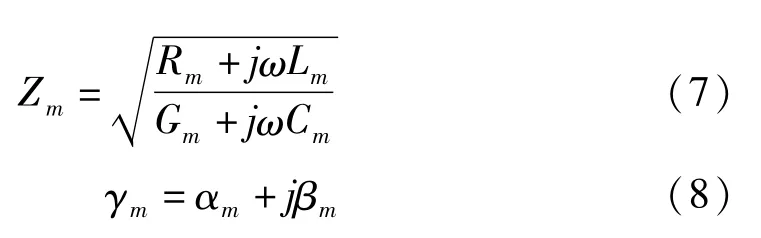
模行波分量的传播速度为：

式中：k=0、1、2；Rm、Lm、Gm、Cm分别为模域中单位长度的电阻、电感、漏电导、漏电容；αm为衰减系数，βm为相位畸变系数。

故障行波分量中零模分量在传播过程中的衰减和相移最为严重，这是因为零模分量受零序电感和电阻的影响较大，零序电感和电阻因大地回路的集肤效应而与频率密切相关［6］。零序电感随频率升高而明显降低，零序电阻随频率升高而明显增大，这就导致零模中频率分量越高，传播过程中衰减越严重，在测量端检测到的零模波速越低。而线模受正序电感和电阻的影响较大，但正序电阻和电感的参数受频率变化的影响要小得多，因而线模分量受频率的影响远不及零模所受的影响，即线模波速稳定。仿真结果见表1。

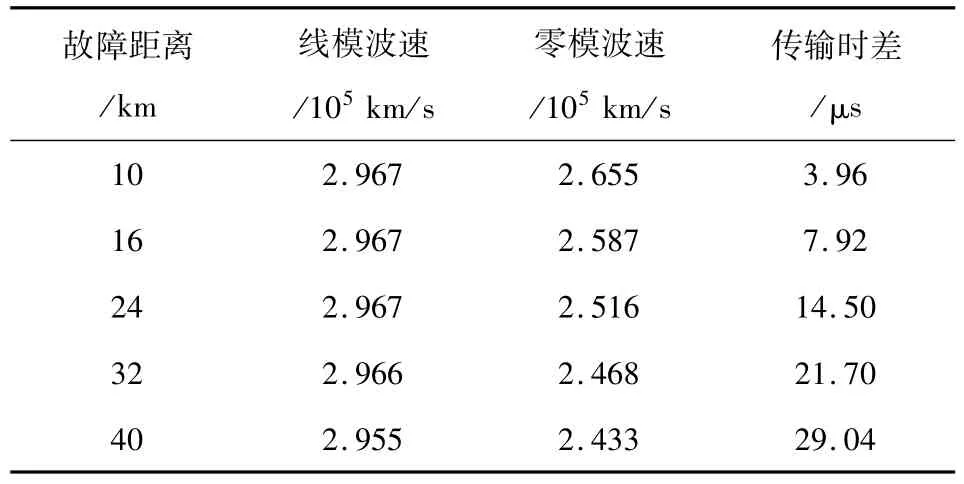
表1 故障行波仿真结果表

由表1可以看出，随着故障距离的增加，线模检测波速基本不变，后文仿真中均采用线模波速为2．967×105km／s，而零模检测波速单调减小，两模量传输时差单调增加。

2．2 零模波速的估算

由上文分析可知，随着传输距离的增加，零模检测波速单调递减，而两模量传输时差则单调递增，由于两者都随距离单调变化，两者之间必然有一定的对应关系，如果得到它们之间的这种对应关系的表达式，便可以用传输时差对零模波速进行估算，但这种关系又很难用具体的数学表达式来表示。本文考虑通过神经网络［7］的训练和学习刻画这种对应关系。

要尽可能准确地估算出行波零模波速，训练样本要针对不同单相接地故障情况（不同的接地电阻、不同的接地时刻、不同的故障距离等）进行选取。利用PSCAD中依频特性线路模块搭建电力系统单相接地故障仿真模型，采样频率设置为10 MHz，训练样本依据下列条件进行选取：

1）接地电阻选取为30Ω、200Ω。2）故障距离的选取步长为0．7 km，故障线路全长为70 km。3）接地时刻电压相角为60°、0°、-60°

仿真后得到各种故障数据，利用小波变换将这些仿真数据进行处理后，将在测端检测到的行波线模分量、零模分量的传输时差与零模波速一一对应，作为训练样本，这样共有600组训练样本，将它们进行归一化处理，随机选取500个样本作为训练样本，剩下的100个作为测试样本。而后送入神经网络进行训练学习。选取自适应学习速度算法作为神经网络的训练算法，最大训练次数定为104次，目标函数误差定位10-5。神经网络的估算结果见表2。

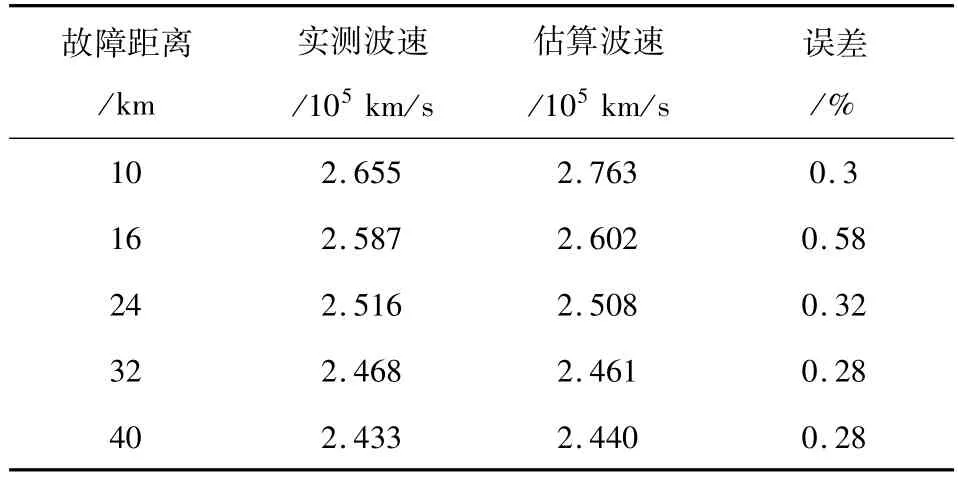
表2 神经网络估算结果表

从表2可以看出，估算得到的波速度和实测波速度基本一致，误差最大不超过1%，能够达到工程应用的要求。

3 仿真验证

MATLAB数据运算处理能力较强，可用作故障数据处理的软件。试验仿真研究采用电磁暂态仿真软件PSCAD，采用依频特性的线路模型，采样频率设为10 MHz。

仿真模型设置为矿区10 kV供电系统常见的单端辐射状供电网络。10 kV母线上有4条出线，M为测量端，MA=21 km，MB=33 km，MC=28 km，MD= 25 km，见图3。

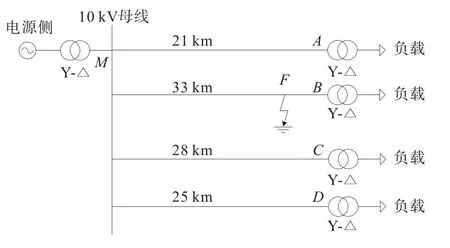
图3 仿真系统模型图

算例一：假设在0．004 s时刻，线路MB发生A相接地故障，故障距离MF=8 km，过渡电阻为10Ω。故障发生后，将采集到的数据送入MATLAB中进行分析。故障电压行波零模分量及线模分量的波形见图4。

然后利用小波分析工具，选用Db6小波函数分别对零模分量和线模分量进行小波变换，找到突变点即其行波到达测量端的时刻，见图5。

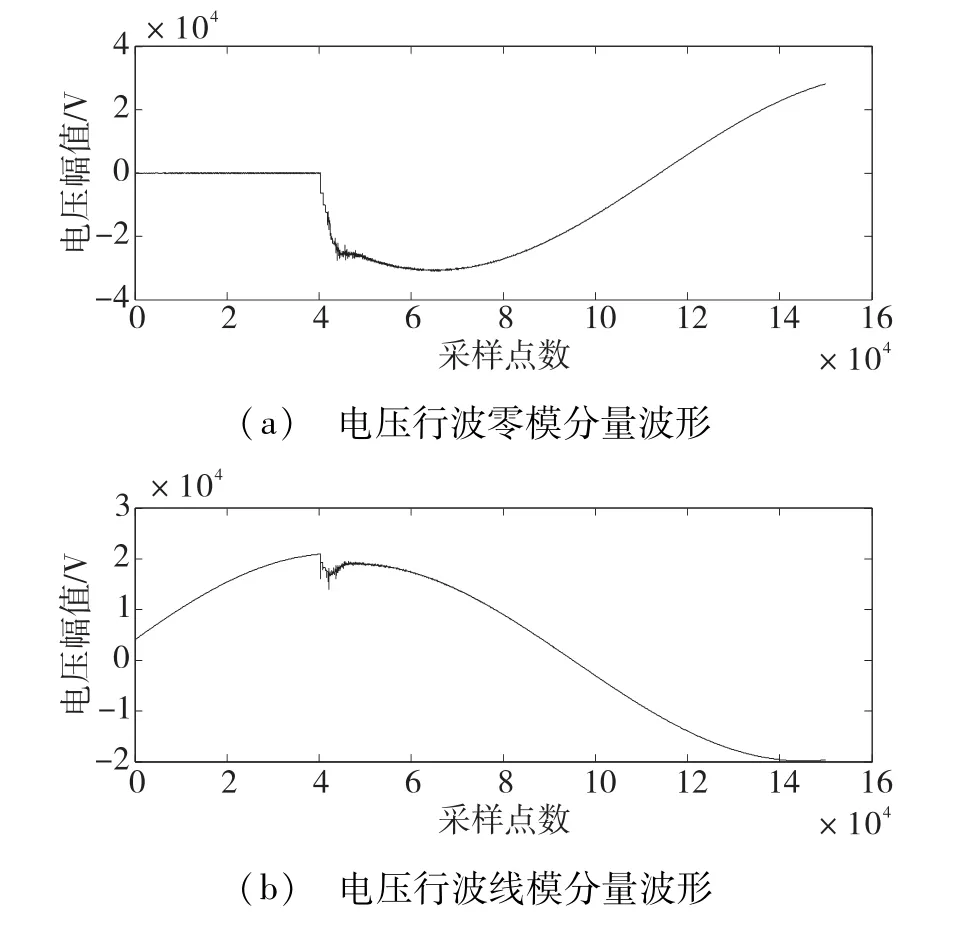
图4 8 km处故障时电压行波波形图

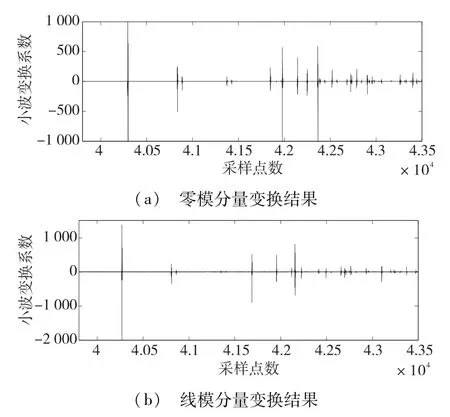
图5 8 km处故障时电压行波小波变换结果

对首个突变波头进行局部放大，得到图6。

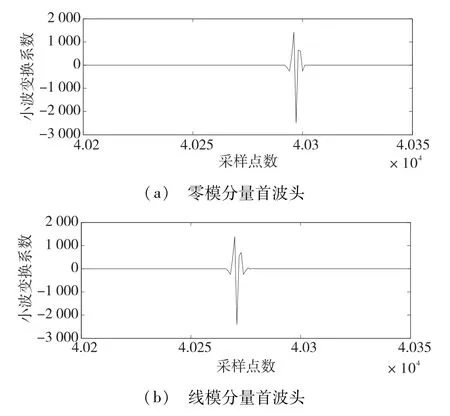
图6 8 km处故障时小波变换结果局部放大

从仿真结果可得，线模行波初始行波达到测量端的时间为第40 270点；零模行波初始波头达到测量端的时间为第40 296点；则零模行波和线模行波的波头相差26点，由采样频率为10 MHz得到两者的传输时差为2．6μs，将此传输时差送入已经训练好的神经网络，估算出零模波速为v0=2．714×105km／s，代入测距公式：

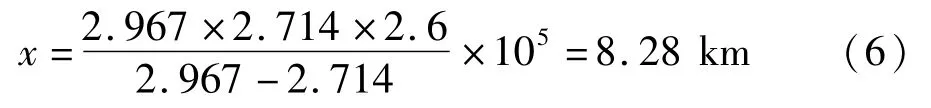
可见，由于对零模波速估算的误差，导致最终得到的故障有0．28 km的误差，但该结果能够为运行人员排除故障点提供重要的参考依据。

算例二：假设在0．006 s时刻，线路MB发生A相接地故障，故障距离MF=20 km，过渡电阻为200Ω。行波零模分量和线模分量首个波头达到测量端的时刻见图7。

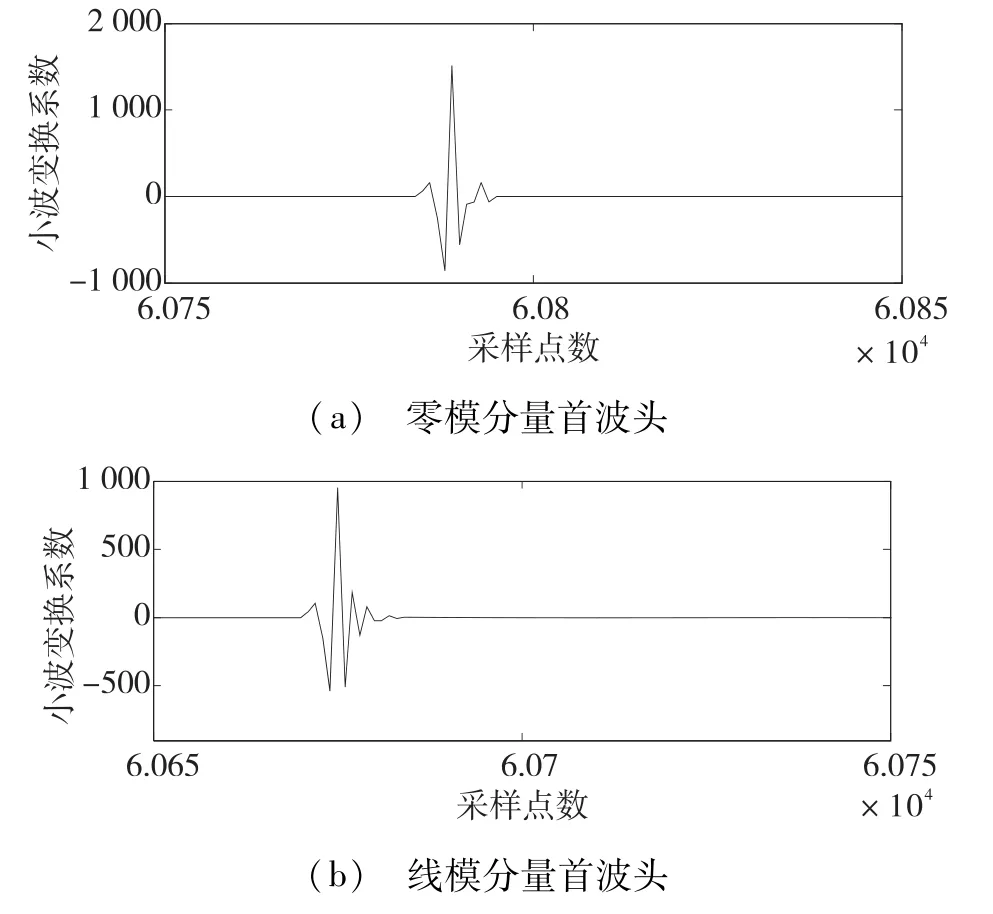
图7 20 km处故障时小波变换结果局部放大

线模行波初始行波达到测量端的时间为第60 672点；零模行波初始波头达到测量端的时间为第60 786点；两者的传输时差为11．4μs，将此传输时差送入已经训练好的神经网络，估算出零模波速为v0= 2．529×105km／s，代入测距公式（6）得到故障距离x =19．53 km，误差为0．47 km。

不同故障情况下的仿真测试结果见表3，可以看出针对各种不同的故障情况，该方法均能较为准确地得到故障距离。

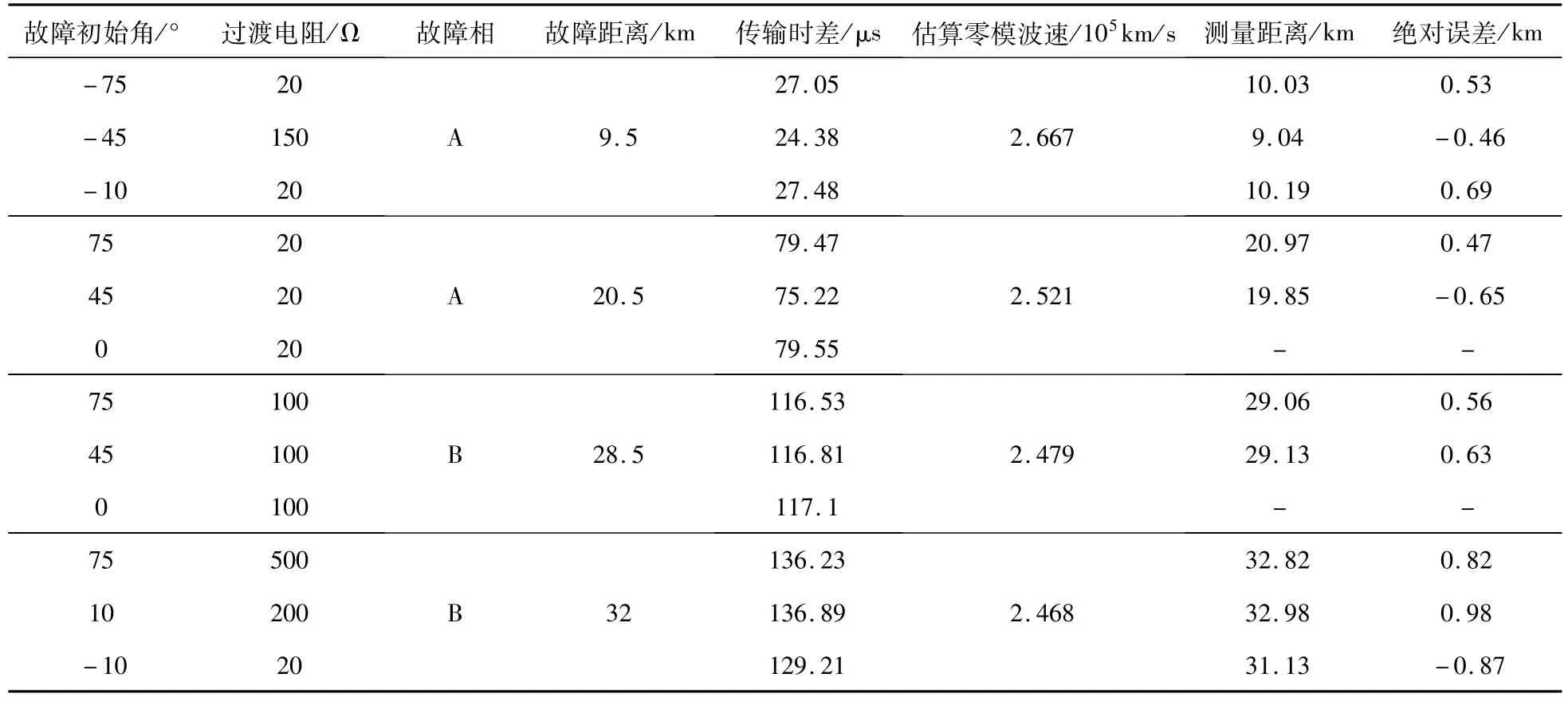
表3 不同故障情况下的仿真测试结果表

传统的单端行波故障测距法由于不能很好地区分故障点反射波、对端母线反射波及健全线路反射波的限制，而限制了其使用，当利用模量波速差进行故障测距时，由于零模波速的不稳定性导致测距误差很大。本文通过BP神经网络训练学习功能来解决零模波速不稳定的问题，且仅需识别首个突变波头，不受后续杂乱波头的影响。

4 总 结

1）通过凯伦鲍尔变换将暂态电流行波转换为没有电磁耦合的模分量，零模波速具有较强的依频特性，由于受到零模波速不稳定的影响导致基于模量波速差的行波故障测距误差较大。

2）鉴于零模波速v0与行波时差△t之间具有特定的对应关系，通过BP神经网络训练学习，用行波时差△t来估算零模波速v0，然后基于模量波速差实现对故障距离的初测。

3）行波测距分为时域法和频域法，本文是从时域法考虑进行行波测距，现在频域法的行波故障测距也有很多学者在研究，在后续的学习中可将时域法和频域法进行结合，融会贯通，也许会取得更好的定位效果。

［1］ 邬林勇，何正友，钱清泉．单端行波故障测距的频域方法［J］．中国电机工程学报，2008，28（25）：99-104．

［2］ 黄子俊，陈允平．基于小波变换模极大值的输电线路单端故障定位［J］．电力自动化设备，2005，25（2）：10-13．

［3］ 林 圣，何正友，陈 鉴，等．基于行波时频特征的单端故障测距方法［J］．电网技术，2012，36（1）：258-264．

［4］ 季 涛．中性点非有效接地系统行波故障测距技术［M］．北京：北京理工大学出版社，2008：46-56．

［5］ 张 帆，潘贞存．基于模量行波传输时间差的线路接地故障测距与保护［J］．中国电机工程学报，2009，29（10）：78-83．

［6］ 覃 剑，陈祥训，郑健超．行波在输电线上传播的色散研究［J］．中国电机工程学报，1999，19（9）：27-32．

［7］ 束洪春，邬乾晋，张广斌，等．基于神经网络的单端行波故障测距方法［J］．中国电机工程学报，2011，31（4）：85-92．

Fault Location in Coal Mine Power Distribution Systems

Wang Jian-liang

The special wave head cannot be effectively identified for the conventional single-ended traveling wave fault location and because the destabilizing effect of the zero-mode phase velocity bring about big error of traveling wave fault location result based on the modulus wave velocity difference．Aimed at these problems，this paper analyzed the zero-mode detection wave velocity monotonically decreasing with transmission distance increasing，meanwhile the transit time difference of the two modulus are monotonically increasing．Thus estimated zero-mode phase velocity based on BP neural network，and then used modulus wave velocity difference for fault location．Simulation shows that the method is applicable and has high precision for various fault conditions．

Coal mine power grid；Single phase grounding；Fault location；Phase-model transformation

TD61

A

1672-0652（2013）10-0004-05

2013-07-17

王建亮（1967—），男，山西寿阳人，1988年毕业于阜新矿业学院，高级工程师，主要从事煤矿供电安全管理工作（E-mail）sxxsmddhsy＠163．com