20 kV 线路经济供电半径

李 敏，冯 宇，程 杰

（1.中国电力科学研究院，武汉430074；2.湖北省电力勘测设计院，武汉430024）

城市电网的发展改造是随着用电需求的增长和负荷密度的增加而进行的。随着国民经济的发展和人民生活水平的提高，城市的用电水平不断上升，采用10 kV 供电所暴露出来的问题已日渐明显。配网电压等级采用20 kV 与采用10 kV 相比，前者可以增加供电能力，增大供电半径，降低线损，降低单位负荷的建设投资和运行费用。我国有很多地区都开展了20 kV 电压等级的研究，在苏州工业园区已采用了220/110/20/0.4 kV 的降压层次，国内有些经济发达地区也准备开展220/20/0.4 kV 的试点项目。本文旨在研究220/110/20/0.4 kV 和220/20/0.4 kV 供电方案20 kV 电缆线路和架空线路的经济供电半径。根据电网的实际情况，对全电网建设综合投资、电网公司营业收入情况、运行费用等进行经济比较，从而科学、合理地确定20 kV线路的经济供电半径，于此同时变电站变电容量、线路条数、长度都可以确定，就可以据此初步判断电网的建设规模，这对于通过负荷预测进行电网规模的规划具有指导意义。

1 计算模型的建立

1.1 经济分析方法

在以往研究线路经济供电半径时，常采用年总费用法计算。年总费用法是将技术方案从开始施工到基建结束年份的投资，折算到基建结束年份，然后将折算后的总投资平均分摊到方案服务年限的每一年，和年运行费用相加，得到的便是年总费用。

年总费用法是静态经济分析评价方法中的一种，对于评价项目的盈利能力而言相对欠缺，所以在实际的项目评价中可以结合动态经济效果评价指标来进行评价，而净现值法就是目前工程建设中广泛采用的动态经济效果评价方法之一。

净现值（net present value，NPV）法的优点是考虑资金的时间价值，符合市场经济的需要，同时考虑了投资项目的整个分析期内的经营情况。它直接用金额表示投资项目的收益性和收益能力，非常直观。由于净现值法考虑了项目有效期内的全部净现金流量，即除包含现金流出（投资等）外、还包含了现金流入（售电收入等），在项目有效期内的一切费用（包括投资和运行费用）和效益都考虑了时间因素，即按照贴现的方法，将不同时期发生的费用和效益折算为现值。因此用净现值法进行经济分析，可以较全面反映电力项目总投资的经济效果。两种方法的比较如表1 所示。

表1 年费用法、净现值法比较Tab.1 Comparison of annual cost method and NPV method

文献[1-4]研究中，均采用的是年总费用法，并在求解经济供电半径的过程中使用求导的方法，在计算过程中并未考虑到变电站容量限制条件和线路电压降限制条件。本文采用净现值法动态分析求解出变电站经济供电半径，并在求解过程中考虑到变电站容量限制条件和线路电压降限制条件。

净现值法是以净现值和净现值率为基础进行经济分析比较的方法。所谓净现值是指将投资项目在有效期内或寿命期内的净现金流量按一定的折现率全部折算到零期的累计现值之和。如果净现值大于零，说明该方案除能满足预定的收益率要求外，还有盈利，项目在经济上是可行的。净现值越大，投资项目就越优[5]。

NPV 的表达式为

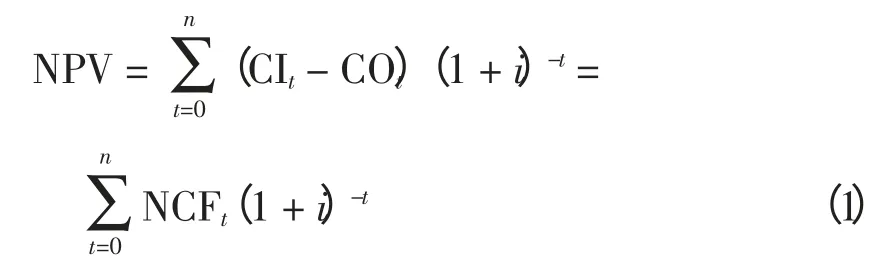
式中：CIt为第t年现金流入量；COt为第t年现金流出量；NCFt为第t年净现金流量，NCFt= （CIt-COt）；n 为项目寿命期或有效期；i 为项目基准报酬率或折现率。

本文中所取的目标函数是投资有效期内单位负荷的净现值（NPV0）。

1.2 模型假设条件

（1）220 kV（110 kV）变电站供电区域为圆形，变电站位于圆心，供电区域内，负荷均匀分布。

（2）配电网呈辐射结构，且不同的配电网结线方式相同（即在同一可靠性下）。

（3）110～220 kV 变电站均按3 台主变规划，首要考虑横向备用，满足N-1 准则。

（4）经济计算中，“现金流入”项只计售电收入和回收固定资产余值，“现金流出”项只计配电网建设投资、经营成本和所得税。

1.3 经济分析数学模型建立

1.3.1 建设总投资C4（万元）

1）220 kV（110 kV）变电站建设投资C1（万元）

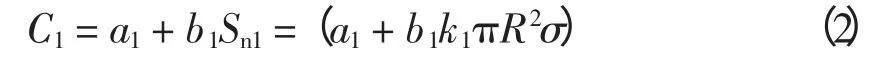
式中：Sn1为220 kV（110 kV）变电站容量，MVA；R为220 kV（110 kV）变电站供电区域半径，km；σ 为平均负荷密度，MW/km2；k1=1/（k1′cos ψ），k1′为220 kV（110 kV）变电站运行率；a1为与220 kV（110 kV）变电站容量无关的投资部分系数，万元；b1为与220 kV（110 kV）变电站容量相关的投资部分系数，万元/MVA；cos ψ 为系统功率因数。

2）20 kV 线路建设投资C2（万元）

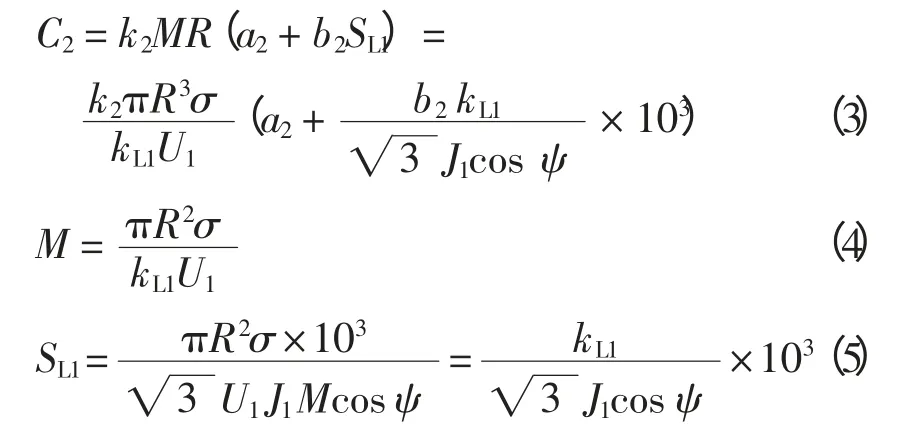
式中：M 为220 kV（110 kV）变电站20 kV 出线回路数；SL1为20 kV 出线平均截面积，mm2；U1为20 kV 电压等级，kV；k2为20 kV 线路曲折系数；J1为20 kV 导线计算电流密度，A/mm2；kL1为每回20 kV出线平均负荷系数，MW/kV；a2为与20 kV 导线截面无关的投资部分系数，万元/km；b2为与20 kV 导线截面相关的投资部分系数，万元/（mm2·km）。

3）中压配电站建设投资C3（万元）

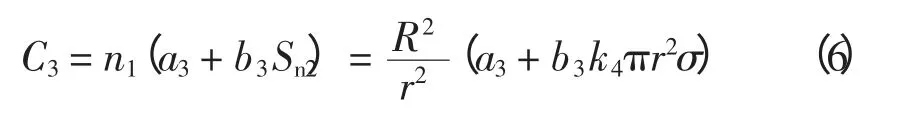
式中：Sn2为中压配变容量，kVA；n1为配电站的数量；k4为配变容载比；a3为与配电站额定容量无关的投资部分系数，万元；b3为与配电站额定容量相关的投资部分系数，万元/kVA；r 为20 kV 变电站供电区域半径，km。

4）建设总投资C4（万元）

1.3.2 年总电能损耗费用C8（万元）

1）220 kV（110 kV）主变年电能损耗费用C（5万元）

220 kV（110 kV）主变的年电能损耗为

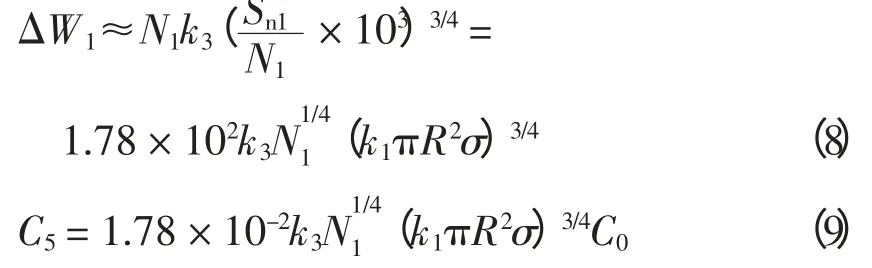
式中：k3为220 kV（110 kV）主变等效损耗系数，k3={k3′×8 760+k3″（k1′）2τ1}；k1′为220 kV（110 kV）主变运行率，k3′和k3″分别为220 kV（110 kV）主变铁耗、铜耗折算系数，τ1为220 kV（110 kV）主变年最大负荷损耗时间，h；N1为220 kV（110 kV）变电站主变台数；C0为损耗电能单价，元/（kW·h）。

2）20 kV 线路电能损耗C6[6-8]（万元）

M 条出线总损耗为

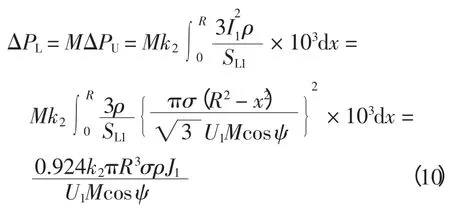
一年总线损为

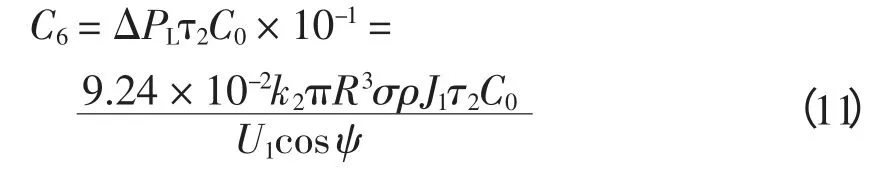
式中：τ2为20 kV 线路及20 kV 配变年最大负荷损耗时间，h；ρ 为电阻率，Ω·mm2/m；I1为线路电流，A。

3）20 kV 配变电能损耗费用C7（万元）

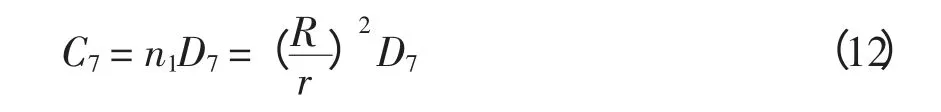
中压配变的年电能损耗为

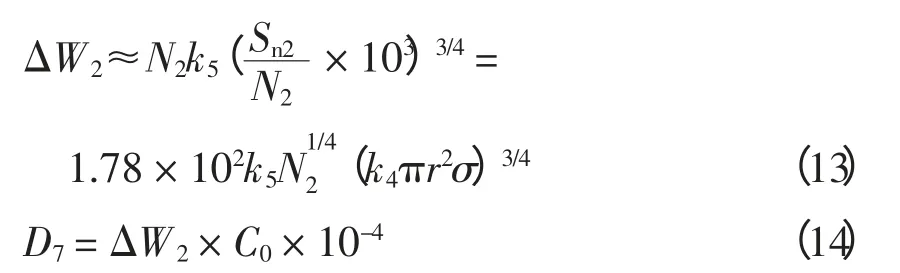
式中：N2为20 kV 配电站配变台数；k5为中压配变的等效损耗系数，k5= {k5′×8 760+k5″（k4′）2τ2}，k5′和k5″分别为中压配变铁耗、铜耗折算系数；k4′为中压配变运行率。

4）年总电能损耗费用（万元）

1.3.3 目标函数——单位负荷净现值（NPV0）

建设期和经营期净现金流量的计算公式可分别描述为：

又假设全部投资在建设起点一次投入，建成后1～n年每年经营净现金流量相等（不含回收额，投资的回收采用直线折旧法），第n年（经济使用寿命期末点）固定资产净残值为k0C4，则每年净现金流量（NCF）为

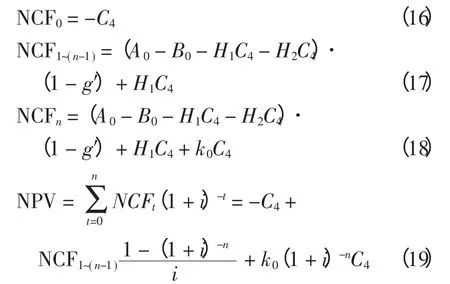
单位负荷容量的净现值为

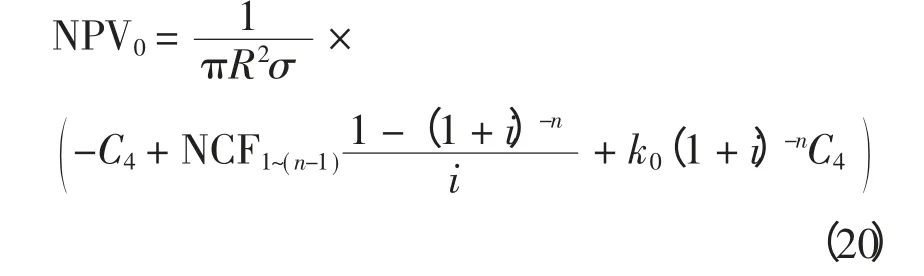
式中：A0为年营业收入，A0= πR2σT3G0× 10-1，万元；B0为年购网电费，B0= （A0/G0+C8/C0）Q0，万元，Q0为购电单价，元/（kW·h），G0为售电单价，元/（kW·h），C0为损耗单价，元/（kW·h）；g′为所得税率；k0为固定资产净残值系数；H1为固定资产折旧系数，H1=（1-k0）/n；H2为维护、检修费用系数；T3为中压配变年负荷最大运行小时数，h；n 为经济使用寿命期，a。

2 20 kV 经济供电半径求解

2.1 目标函数的约束条件

计算以单位负荷的净现值NPV0为目标函数，求解的目标是使NPV0最大。计算过程中，函数的约束条件如下。

（1）变电站容量限制，即

式中：k 为变电站容载比；Smax为变电站最大容量。

各种类型变电站单台容量取值如表2 所示。

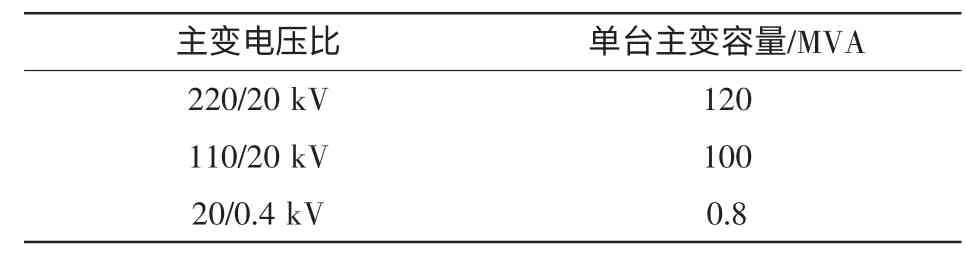
表2 各种类型变电站单台容量取值Tab.2 Single transformer capacity of all kinds of substations

（2）线路的电压降限制。

计算公式为

式中，R0和X0分别为线路单位长度的电阻和感抗，Ω/km。

显然，上述问题是一个带有约束条件的非线性规划问题，本文采用罚函数法编制计算机程序进行优化求解。

2.2 相关系数的取值

变电站、20 kV 线路和配电站相关系数参见表3～表5。经济参数如表6 所示。

表3 变电站相关系数取值【9-13】Tab.3 Correlative coefficients of substations

表4 20 kV 线路相关系数Tab.4 Correlative coefficients of 20 kV lines

表5 配电站相关系数Tab.5 Correlative coefficients of substations

表6 经济参数Tab.6 Correlative economic coefficients

2.3 计算结果

由于线路建设投资与供电半径的三次方成正比，所以当变电站的位置固定时并不是供电半径越大经济效益越好，随着供电半径的增大，线路的投资呈三次方的递增，会使单位负荷的净现值呈现先增大后减小的趋势，所以存在有一个半径值即经济供电半径使得单位负荷的净现值最大。表7列出了编程计算出的不同供电方案的经济供电半径值。

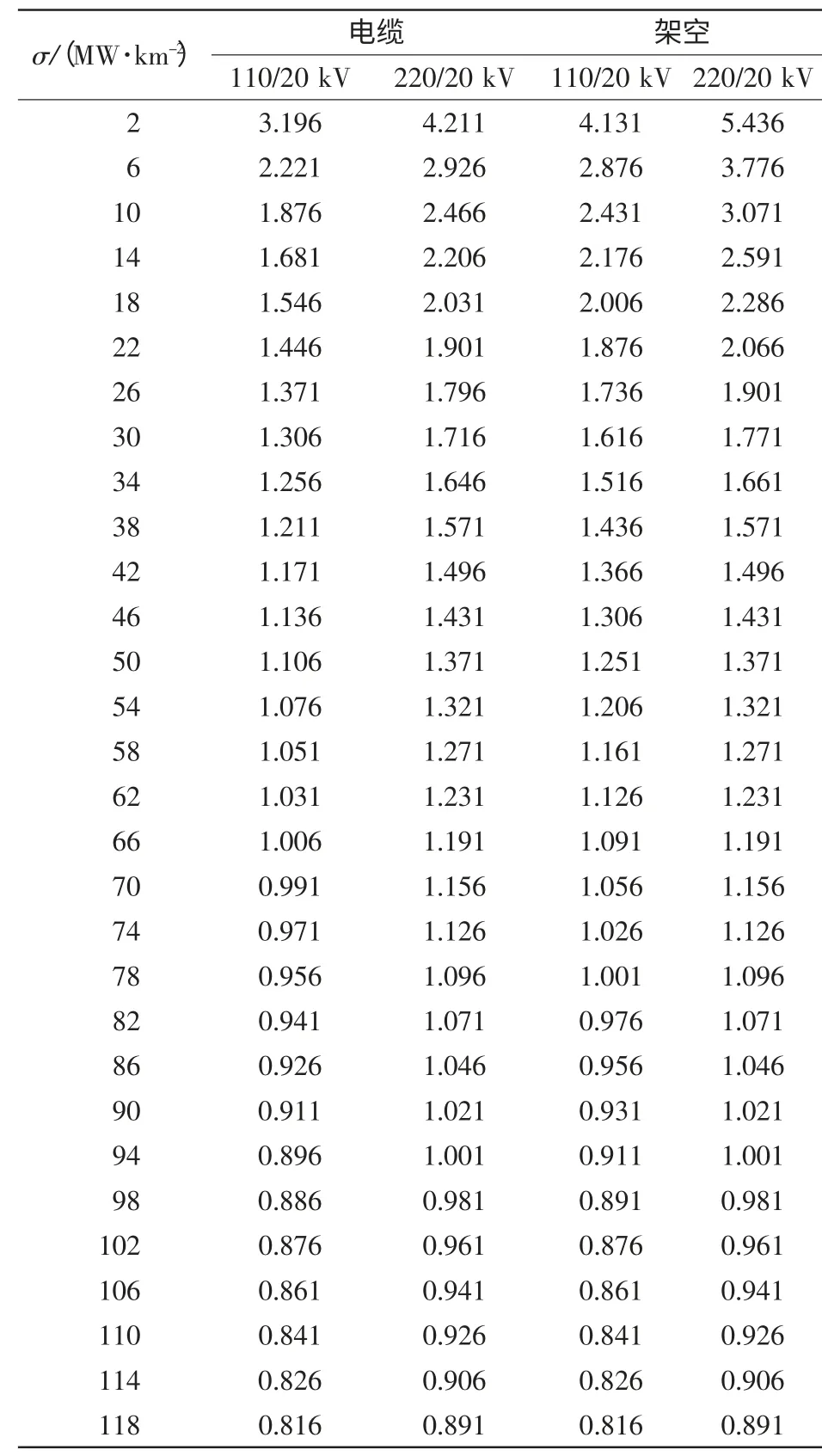
表7 20 kV 线路经济供电半径Tab.7 Economical radius of 20 kV lineskm

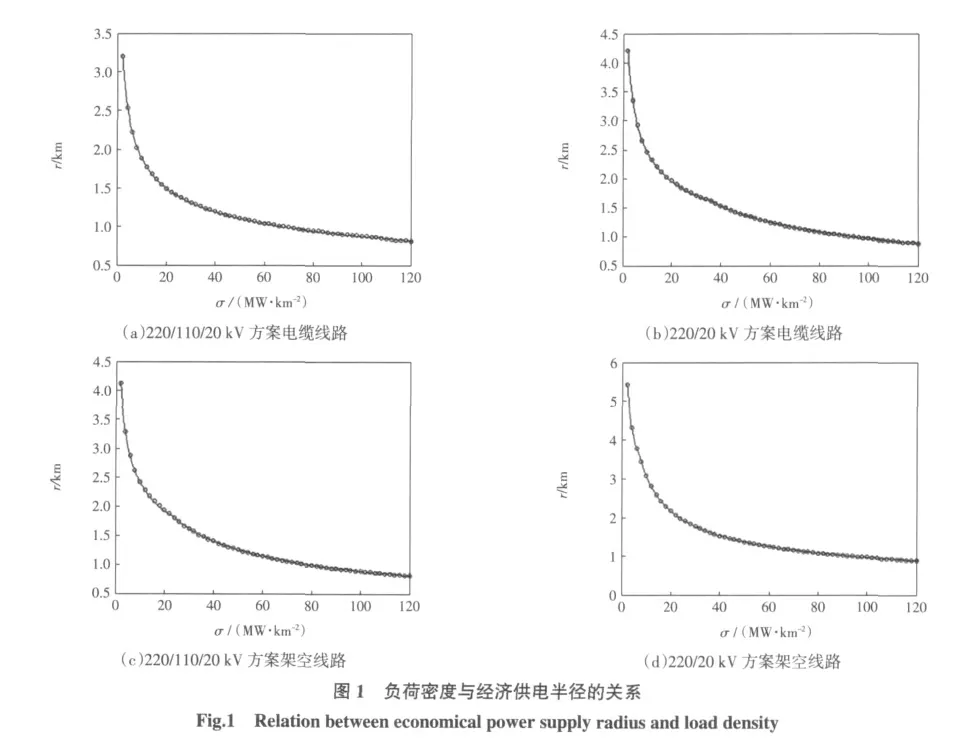
通过对表7 数据的分析，本文利用拟合的方式，拟合出20 kV 电缆线路和架空线路经济供电半径与负荷密度的关系式，见表8。图1 中圆圈为表7 中数值，曲线为表8 中的表达式。

结果分析如下。

（1）以单位负荷的净现值最大为目标，优化计算出20 kV 电缆线路和架空线路经济供电半径与负荷密度的关系，即在低负荷密度区经济供电半径Re∝σ-1/3，在高负荷密度区Re∝σ-1/2。

（2）在第2.1 节目标函数的约束条件中，变电站容量限制条件比线路的电压降限制条件苛刻，即满足变电站容量限制的最大半径值比满足线路电压降限制的最大半径值小。因此可推出

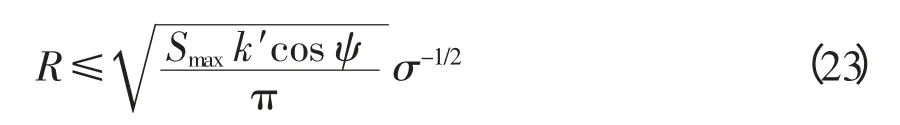
式中，k′为主变运行率。根据计算结果可知，当负荷密度大到一定程度时，变电站经济供电半径即为供电半径的限制值，即

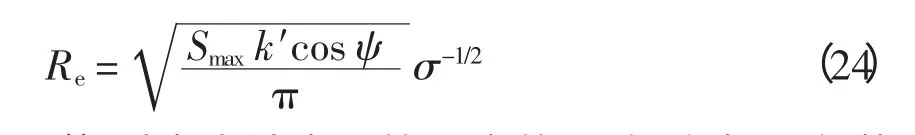
（3）受变电站容量等因素的影响，在相同负荷密度的条件下，220/20 kV 方案对应的经济供电半径比220/110/20 kV 方案大。

表8 20 kV 电缆线路和架空线路经济供电半径Re 与负荷密度的关系式Tab.8 Relation table between economical power supply radius and load density

3 结论

（1）本文运用净现值法，在全面考虑电网建设综合投资、电网公司营业收入情况、运行费用等因素的条件下，科学合理地建立了经济计算模型。与传统的年总费用法不同的是，净现值法考虑了企业的营业收入情况，本文采用的净现值法更适用于项目决策的最后评估。

（2）本文首次提出220/20/0.4 kV 方案的经济供电半径的研究。本文采用罚函数法编制程序进行优化求解和数值拟合的方法求出了220/110/20/0.4 kV 和220/20/0.4 kV 供电方案下20 kV 电缆线路和架空线路的经济供电半径和负荷密度的关系式。

（3）传统方法在求解经济供电半径的过程中往往采取求导的方法，而在求导过程中忽略了变电站容量限制及线路的电压降限制条件。本文全面考虑了变电站容量限制及线路的电压降限制条件下，采用罚函数法编制程序进行优化求解、数值拟合的计算方法及全面的分析，总结出：在低负荷密度区经济供电半径Re∝σ-1/3，在高负荷密度区Re∝σ-1/2。当负荷密度大到一定程度时，变电站经济供电半径即为供电半径的最大值，即

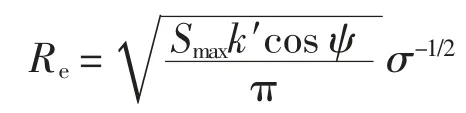
[1]刘友强，李欣然（Liu Youqiang，Li Xinran）.变电站经济容量和经济供电半径的探讨（Discussion on economical capacity and economical power supply radius for transformer substations）[J]. 广东电力（Guangdong Electric Power），2005，18（11）：7-9.

[2]于永源，王贤正，杨绮雯（Yu Yongyuan，Wang Xianzheng，Yang Yiwen）.变电所经济供电半径的优化选择（Optitionnal selection for substation feed economic radium）[J].电力科学与技术学报（Journal of Electric Power Science and Technology），1991，6（1）：118-124.

[3]张秀然，孙国凯，朴在林，等（Zhang Xiuran，Sun Guokai，Piao Zailin，et al）.66/10 kV 配电线路经济供电半径的探讨（Economical radius of power supply for 66/10 kV distribution line）[J]. 农村电气化（Rural Electrification），1997，11（8）：4-6.

[4]张秀然，孙国凯，杨涛（Zhang Xiuran，Sun Guokai，Yang Tao）.经济供电半径的实用计算方法与分析（The practical count method and analysis of economic power supply radius）[J].沈阳农业大学学报（Journal of Shenyang Agricultural University，1998，29（3）：249—250.

[5]张纯.电力经济与管理[M].北京：中国电力出版社，1998.

[6]温建春，韩学山，张利（Wen Jianchun，Han Xueshan，Zhang Li）.一种配电网理论线损计算的改进算法（Improved method for theoretical line loss calculation of distribution network） [J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（4）：72-76.

[7]彭新宇，黄民翔，许诺，等（Peng Xinyu，Huang Minxiang，Xu Nuo.et al）.10 kV 配电网线损的快速计算法（Fast method of 10 kV power distribution network′s energy loss calculation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2002，14（4）：45-47.

[8]范明天，张祖平. 中国配电网发展战略相关问题研究[M].北京：中国电力出版社，2008.

[9]Q/GDW 156—2006.城市电力网规划设计导则[S]. 北京：中国电力出版社，2007.

[10]刘振亚.国家电网公司输变电工程典型造价（2007 版）[M].北京：中国电力出版社，2008.

[11]吴夕科（Wu Xike）.南方电网城市配电网供电电压等级研究报告（Voltage grade study of urban distribution network in China southern power grid）[R].武汉：武汉高压研究所（Wuhan：Wuhan High voltage Research Institute），2005.

[12]郑正圻（Zheng Zhengqi）.20 kV 电压等级论证（20 kV voltage grade research） [R]. 武汉：武汉高压研究所（Wuhan：Wuhan High voltage Research Institute），1994.

[13]熊振东，程鹏（Xiong Zhendong，Cheng Peng）.中压配电网供电方案经济性分析（Economy analysis on power supply scheme of medium voltage distributiong network）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2010，22（1）：150-155.