VSC-HVDC 输电系统的无源性控制器设计

李升来，王 奔，刘向向，侯荣均

（西南交通大学电气工程学院，成都610031）

随着可控关断型电力电子器件绝缘栅双极型晶体管IGBT（insulated bate bipolar transistor）、可关断晶闸管GTO（gate turn-off thyristor）等和脉冲宽度调制PWM（pulse width modulation）技术的发展，电压源换流器高压直流输电系统VSC-HVDC（voltage source converter based high voltage direct current）越来越受到人们的关注。与传统的高压直流输电系统相比，该输电系统具有可向无源网络供电、无换相失败风险、有功和无功功率可独立控制、以及易于构成多端直流供电系统等优点[1]。

目前，国内外学术界对VSC-HVDC 的数学模型和控制策略已经进行了许多有益的探索，包括采用控制交流侧电压和相位，进而控制交流侧电流的间接电流控制策略[2]，其交流侧电流动态响应较慢；在同步旋转坐标下，采用控制交流侧电流和相位的直接电流控制策略[3]，其内外环采用两级PI来实现，其暂态性能不够理想；采用稳态逆模型，用前馈解耦的方式来实现系统电流快速跟踪和有功、无功功率独立调节的控制策略[4]，其外环建立在逆系统模型的基础上，在大扰动情况下很难保持稳定。此外，采用遗传算法理论，对控制环节有关参数进行优化[5]，从而对控制参数进行优化；采用H∞控制理论，在对输出信号进行分析的基础上，设计次同步阻尼控制器，抑制次同步振荡模式的效果明显，且具有一定的鲁棒性[6]。

本文简要地介绍了VSC-HVDC 的工作原理，建立其在dq 轴坐标系下的数学模型，并将其写成欧拉-拉格朗日EL（Euler-Lagrange）动态方程的形式[7]。通过选择适当的能量函数和阻尼输入矩阵，设计无源控制器，从而实现交流侧电流的快速跟踪和直流侧电压恒定，并且达到有功和无功功率独立控制的目的，最后对所设计的控制器进行仿真验证。

1 VSC-HVDC 工作原理和数学模型

假设两端无穷大VSC-HVDC 输电系统结构如图1 所示，两端换流器均采用VSC，具有相同的拓扑结构。图中，Us1、Ur、is1和Us2、Ui、is2分别为整流侧和逆变侧的双端无穷大电源电压、换流器的交流侧电压和电流；R1、R2和L1、L2为整流侧和逆变侧换流器的等效电阻和电感，其中，R1= R2= R，L1= L2= L；C1、C2、Rdc、L3分别为直流侧两端电容和线路等效电阻、电感值，其中C1= C2=C；Udc1、Udc2为直流侧两端直流电压。

由于VSC-HVDC 系统中的整流器和逆变器的电路结构相同，且与三相电压型PWM 换流器电路相似，所以，可以以整流侧电路为例，建立系统数学模型，如图2 所示。

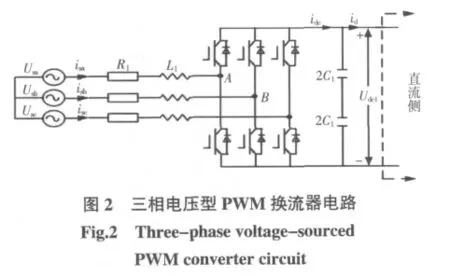
由于R1= R2= R，L1= L2= L，C1= C2= C 则可以得出交流侧的换流器在dq 旋转坐标下的数学模型，即

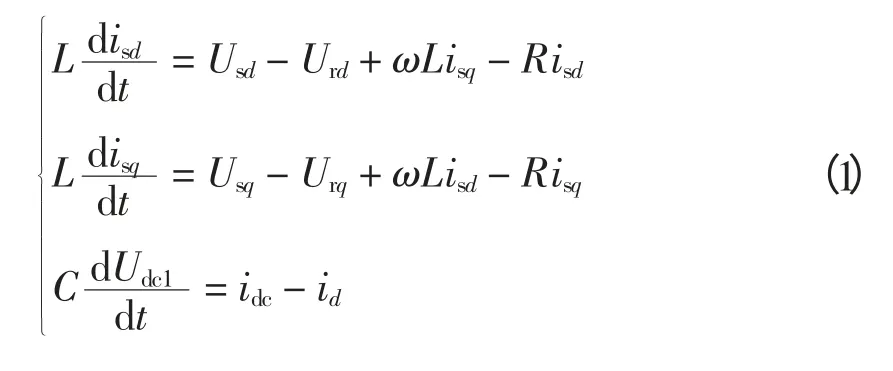
式中：Urd、Urq为VSC 交流侧电压基波的d、q 轴分量；Usq、Usd、isq、isd分别为Usabc，isabc变换后对应的d、q轴分量。考虑到VSC-HVDC 为三相对称系统，所以O 轴分量为0。第三式描述的是直流侧电压的动态特性，首先考虑式（1）中前两个数学表达式，且将它们写成Euler-Lagrange 形式[8]，即

其中：

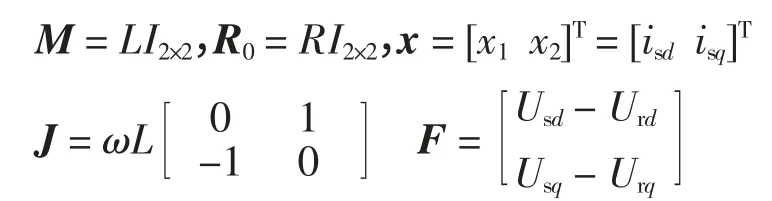
式中：M 为正定的对角阵；J 为反对称阵，反映系统内部的互联结构；R0为对称正定阵，表示系统附加的阻性结构，反映系统的耗散性；F 表示外部输入，反映系统与外界的能量交换；Urd、Urq为系统控制量。

定义能量函数为

式中，W=MR-1M 为对称正定矩阵。对V 求导得，

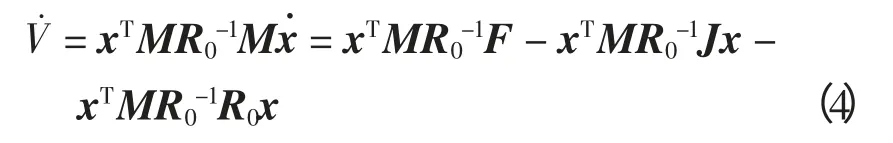
式中：MR0-1J 为反对称阵，所以xTMR0-1Jx=0。令，Q（x）=xTMx，yT=xTMR0-1，因为M 为正定对称矩阵，有Q（x）＞0。

对式（4）两边求积分，

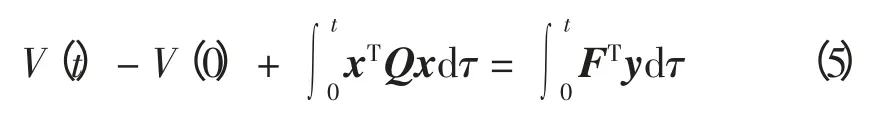
根据无源性系统的判断方法[9]，由式（5）可以得出，式（2）表示的系统是一个严格无源系统。

针对式（1）中的第三个表达式，后面设计了直流侧电压PI 调节器来实现直流侧电压恒定。

2 无源性控制器设计

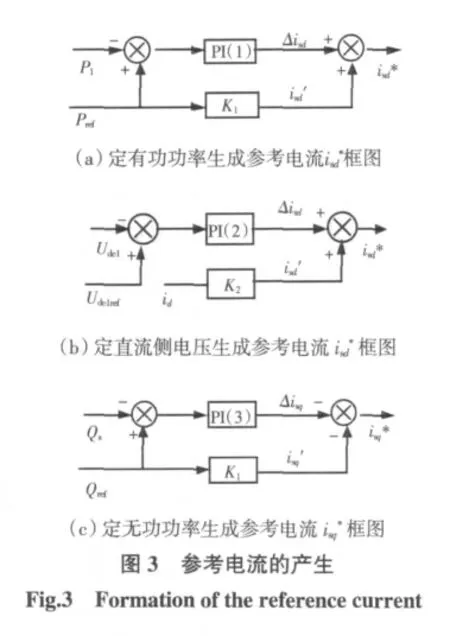
2.1 VSC-HVDC 参考电流计算

设计控制器时，外环控制器整流侧采用定直流电压和定无功功率控制，逆变侧采用定有功和无功功率的控制策略。根据生成的参考电流，设计内环无源控制器进行跟踪，以达到控制有功、无功功率的目的。文中的内环和外环区别于一般的传递函数中的内、外环，而是指系统控制框图图3 所示的内、外环。

根据瞬时功率理论，同时，忽略换流电抗器电阻和开关损耗时，换流站的有功、无功功率和直流侧的有功功率的表达式为

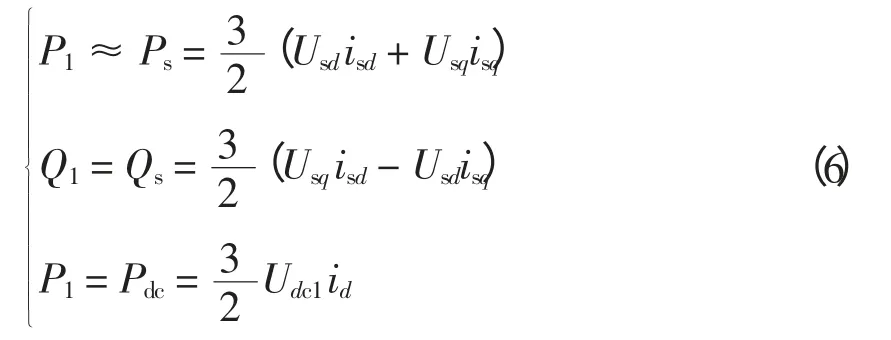
VSC-HVDC 为三相平衡系统，令两端无穷大电源a 相相电压的初相角为0°，有：Usd=Us，Usq=0。将其代入式（6），得到直流侧电压处于稳态时的表达式为

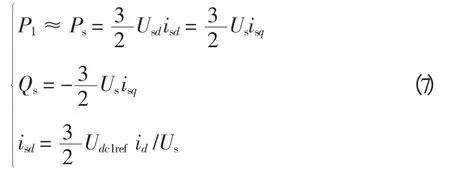
式中，Us为一个恒定值，所以有功、无功功率可以通过调节isd和isq独立来控制。

将式（7）改写成

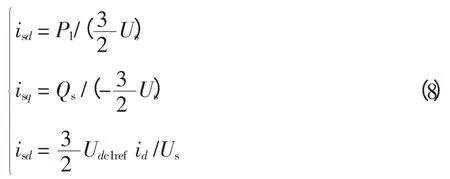
当给定有功、无功功率和直流侧电压的参考值Pref、Qref、Udc1ref，由式（8）得到电流的预估值isd′、isq′。为消除稳态误差，通过三个PI 调节器PI（1）、PI（2）、PI（3），把实际测得的有功、无功功率以及直流侧电压值和给定参考值之间的偏差转化为修正量Δisd和Δisq，然后用相应的预估计值加上修正值，从而得到内环参考电流PI 调节器的参数通过实验得到。相应控制框图如图3 所示。令

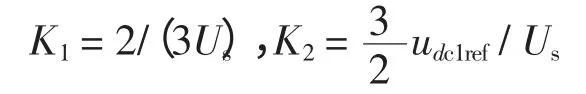
2.2 无源控制器设计

为实现对外环生成的参考电流的跟踪，采用能量整形的方法，来达到理想的平衡点。建立误差系统，令

定义能量函数为

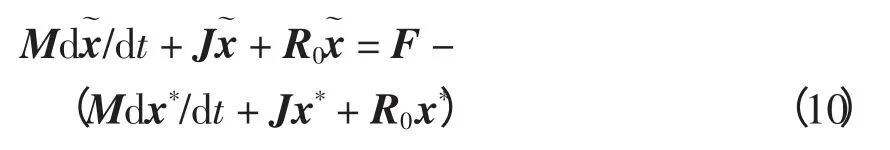
为提高x 向x*的收敛速度，需注入适当阻尼，加入耗散项

将式（11）代入式（10），得

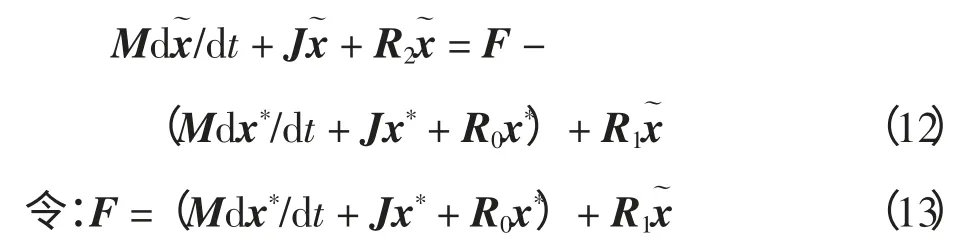
则式（12）得

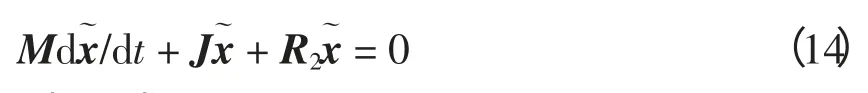
对V1求导，

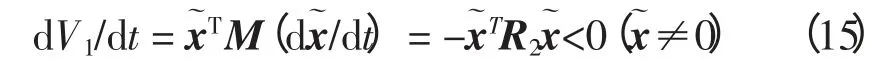
所以电流向参考点渐近收敛，达到平衡点时，式（13）可以化为

将式（2）中矩阵参数代入式（16），得

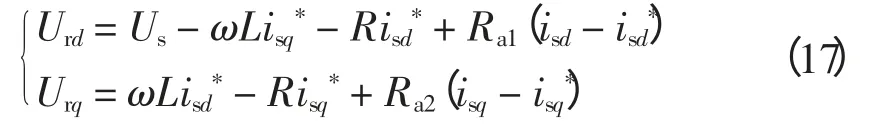
计算得到Urd、Urq。同理，可以计算得到逆变侧的Uiq、Uiq。

至此，无源性控制器设计完成，控制框图如图4 所示。图中，用Ucd、Ucq代替Urd、Urq和Uid、Uiq。当为整流侧时，Ucd、Ucq取Urd、Urq；当为逆变侧时，Ucd、Ucq代替Uid、Uiq。将Ucd、Ucq输入到SVPWM 控制器中，生成换流器的控制信号Sa、Sb、Sc。

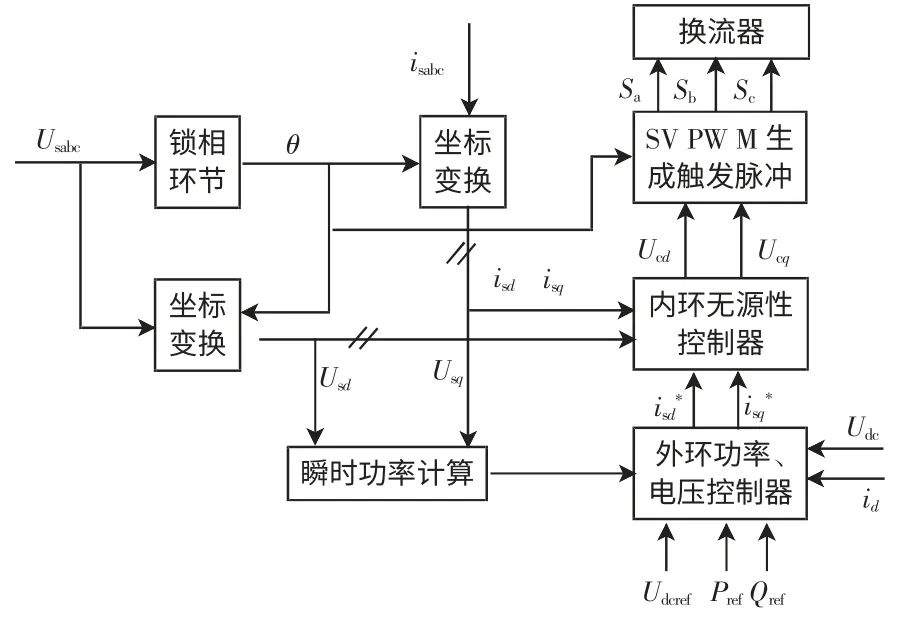
图4 系统控制框图Fig.4 Block diagram of system control

3 仿真分析

为验证所设计控制器的有效性，在Maltlab 中搭建了图1 所示的双端无穷大VSC-HVDC 系统。主要参数如下：系统整流端和逆变端的无穷大母线额定电压Us1=Us2=10 kV，直流侧直流电压的设定值为Udc=20 kV，交流侧电感L1=L2=15 mH，交流侧电阻R=0.2 Ω，直流侧电感L3=20 mH，直流侧等效电阻Rdc=0.5 Ω，直流侧电容C1=C2=7 mF，开关频率为5 000 Hz，换流器额定功率为14 MW。本文采用标幺值表示，交流侧和直流侧的基准功率为12.4 MW，换流站交流侧基准电压为8.16 kV，交流侧电流基准值为1kV；直流侧电压基准值20kV，电流基准为600 A。外环的三个PI 控制器和无源性控制器的参数为：

仿真时，系统整流侧采用定直流侧电压和定无功功率控制；逆变侧采用定有功、无功功率控制。文中所涉及物理量采用标幺值表示，正常稳态运行时，整流侧有功功率为1p.u.，无功功率为0；逆变侧有功功率为-1p.u.，无功功率为0，直流侧电压为1p.u.。

3.1 系统启动实验

取上述参数，假定系统启动前直流电容器电压已经预充到17 kV，仿真结果如图5、6 所示。图5中，分别为双端无穷大电源a 相电压Us1a、整流侧的a 相交流电流is1a、直流电压Udc1、有功和无功功率P1、Q1的响应波形。图6 中，分别为逆变侧的交流电流is2a、直流电压Udc2、有功和无功功率P2、Q2的响应波形。在有功功率、无功功率波形图中，实线表示有功功率，虚线表示无功功率。

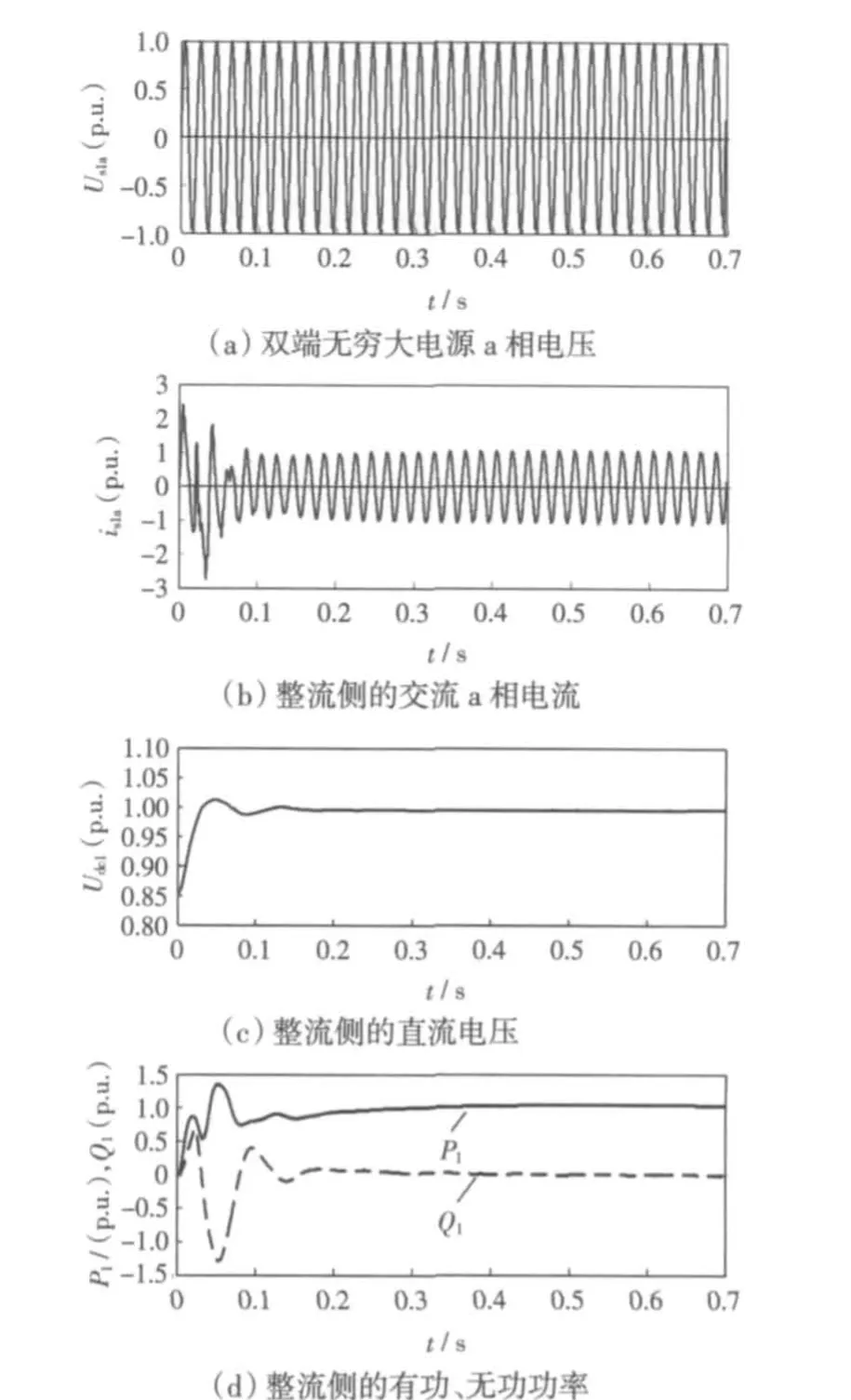
图5 启动实验整流侧的波形Fig.5 Waveforms in the rectifier for startup experiment

通过启动实验可以看出，系统在t=0.3 s 时就很快的到达稳态，而且直流侧电压和有功、无功功率的超调量较小。

3.2 无功功率阶跃响应实验

整流侧无功功率参考值变化如下：在1～1.3 s，为0；在1.3 s，阶跃至-0.2p.u.。逆变侧无功功率参考值变化如下：在1～1.3 s，为0，在2 s，阶跃至0.2p.u.。仿真结果如图7 所示。图7 中分别为整流侧的有功、无功功率P1、Q1和以及逆变侧的P2、Q2的响应以及整流侧直流侧电压Udc1。

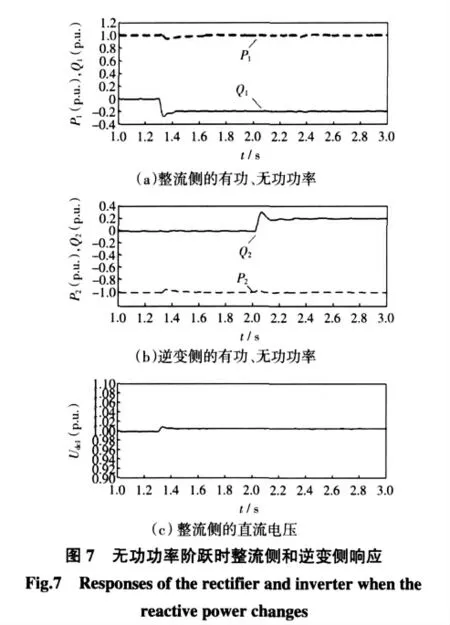
由图7 可以看出，当整流侧和逆变侧无功功率发生阶跃时，直流侧电压有微小的抬升，有功功率几乎不受影响，有功、无功功率可进行独立调节，两换流站的无功功率也可以进行独立调节，且在调节过程中直流电压抖动不超过1%。

3.3 逆变侧三相接地短路故障实验

在t=1.2 s 时，逆变侧发生三相短路，持续时间为五个周期t=0.10 s，仿真结果如图8 和图9所示。图8 中分别为整流器交流侧a 相交流电流is1a，有功、无功功率P1、Q1和直流侧电压Udc1的响应波形；图9 为对应逆变侧的is2a、P2、Q2和Udc2响应波形。

由实验3 可以看出，在逆变侧三相接地短路故障时，整流侧仍能稳定运行，说明整流端和逆变端可以独立进行控制，具有很强的抗干扰能力，且在大扰动消失后能快速恢复到故障前的稳态值。

4 结语

本文建立了VSC-HVDC 输电系统在dq 坐标下的EL 数学模型，设计了无源控制器，并进行了实验仿真验证。仿真结果表明：所设计的无源性控制器具有响应快速、对扰动不敏感、鲁棒性强等优点，使得系统在受到大扰动时直流侧电压和有功、无功功率能快速恢复到故障前的状态，能够快速准确地回到期望的稳态工作点，整流侧和逆变侧控制器均能够实现有功与无功的独立调节。基于无源性理论，结合VSC-HVDC 特有的能量传输特性设计的无源性控制器物理意义明确，结构简单，鲁棒性强，具有较高的理论研究价值。

[1]陈谦，唐国庆，胡铭（Chen Qian，Tang Guoqing，Hu Ming）.采用dq0 坐标的VSC-HVDC 稳态模型与控制器设计（Steady-state model and controller design of a VSC-HVDC converter based on dq0-axis）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（16）：61-66.

[2]陈海荣，徐政（Chen Hairong，Xu Zheng）.基于同步坐标变换的VSC-HVDC 暂态模型及其控制器（Transient model controller design for VSC-HVDC based on synchronous reference frame）[J]. 电工 技术学报（Transactions of China Electrotechnical Society），2007，22（2）：121-126.

[3]Liu Zhongqi，Shao Weijun，Song Qiang，et al.A novel nonlinear decoupled controller for VSC-HVDC system[C]//Asia-Pacific Power and Energy Engineering Conference.Wuhan，China：2009.

[4]包宗贤，邹超（Bao Zongxian，Zou Chao）.向无源网络供电的VSC-HVDC 系统的新型控制器设计（New control design for VSC-HVDC supplying passive networks）[J].电力系统保护与控制（Power System Protection and Control），2008，36（14）：22-27.

[5]陈蔓，陆继明，毛承雄，等（Chen Man，Lu Jiming，Mao Chengxiong，et al）. 基于遗传算法的优化控制在VSCHVDC 中的应用（Application of genetic algorithm based optimal control in VSC-HVDC）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（4）：19-23.

[6]邓婧，李兴源，王渝红，等（Deng Jing，Li Xingyuan，Wang Yuhong，et al）.H_∞控制理论在次同步阻尼控制器设计中的应用（Application of H_∞control theory on subsynchronous damping controller）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（6）：1-5.

[7]王久和，黄立培，杨秀媛（Wang Jiuhe，Huang Lipei，Yang Xiuyuan）.三相电压型PWM 整流器的无源性功率控制（Power control of three-phase boost-type PWM rectifier based on passivity）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（21）：20-25.

[8]Lee Tzann-Shin.Lagrangian modeling and passivity-based control of three-phase AC/DC voltage-source converters[J].IEEE Trans on Industrial Electronics，2004，51（4）：892-902.

[9]王久和.电压型PWM 整流器的非线性控制[M].北京：机械工业出版社，2008.