采用BBPSO 优化SVM 的电机定子故障诊断

王攀攀，史丽萍，杨晓冬，张 涛

（中国矿业大学信息与电气工程学院，徐州221008）

感应电机定子绕组匝间短路故障是导致电机失效的主要原因之一，约占电机故障的30%～40%[1]，因此对电机定子进行早期的检测和诊断具有重要意义。

而感应电机定子的故障诊断问题实质上是状态识别问题。目前，状态识别的方法主要包括模糊理论[2]、神经网络[3]和支持向量机[4，5]等。前二者都是基于大样本的学习理论，难以满足只能提供少量故障样本的诊断识别问题。而支持向量机SVM（support vector machine）是一种基于统计学习理论的机器学习方法，在解决小样本问题中表现出独特的优势和良好的应用前景，并具有优良的泛化能力。但是，在SVM 状态识别过程中，其参数的选取一直是一个难题，影响了它的性能和实用性。

骨干微粒群优化算法BBPSO（bare-bones particle swarm optimization）[6]是一种新兴的全局优化技术，由Kennedy 于2003 提出。由于BBPSO 算法概念简单、无需设置参数、易实现、能有效解决复杂优化问题，因此在科学研究与工程实践中得到了广泛的关注。

本文将BBPSO 算法和SVM 相结合进行感应电机定子匝间短路故障诊断，其中应用BBPSO 算法进行SVM 模型的参数优化。

1 微粒群优化算法和支持向量机

1.1 微粒群优化算法

微粒群优化算法PSO（particle swarm optimization）[7]是由Kennedy 和Eberhart 于1995 最先提出的一种模拟自然生物群体行为的全局优化技术。在PSO 算法中每个微粒就是解空间中的一个解，根据自己的飞行经验和同伴的飞行经验来调整自己的飞行轨迹。每个微粒在D 维空间里的位置表示为矢量xi=（xi，1，xi，2，…，xi，D），飞行速度表示为矢量vi=（vi，1，vi，2，…，vi，D）。每个微粒都有一个被优化函数决定的适应值，并且知道自己到目前为止发现的最好位置pi（称为微粒个体极值）和现在的所处位置xi，这些可以看作是微粒自己的飞行经验。除此之外，每个微粒还知道到目前为止领域中所有微粒发现的最好位置pg（称为微粒全局极值），这个可以看作是微粒同伴的经验。微粒群优化算法是一种基于迭代的优化工具，对于第t +1 次迭代，每个微粒的每一维按如下公式进行变化[7]。

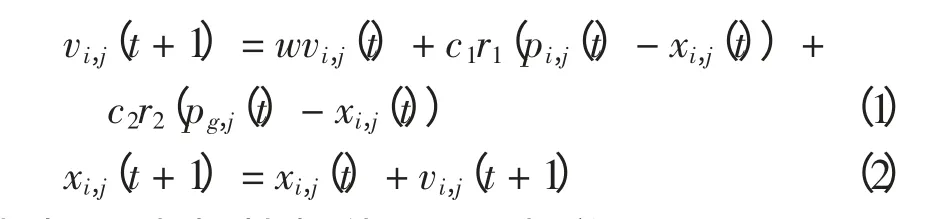
式中：w 为惯性权值；c1、c2为学习因子；r1、r2是[0，1]之间的随机数；vi，j∈[-vmax，vmax]，其中vmax为用户设定的最大微粒速度；i=1，2，…，N，N 为微粒群规模；j=1，2，…，D。

Clerc 和Kennedy 分析了微粒的运动轨迹，证明了在标准PSO 算法中每个微粒i 向它的个体历史极值和全局极值的加权平均值Gi收敛[8]，即

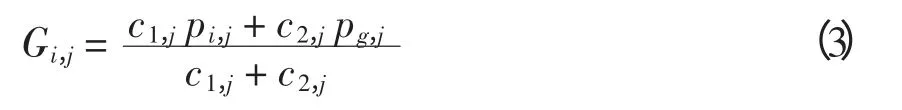
式中，c1，j和c2，j是在[0，1]之间的随机数，当迭代次数趋于无穷时所有微粒将收敛到同一点。

依据这种思想，Kennedy 于2003年，提出了骨干微粒群算法（BBPSO）[6]。BBPSO 算法利用一个关于微粒全局极值点和个体极值点的高斯分布完成微粒位置的更新，即

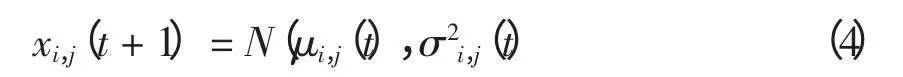
式中：μi，j（t）=（pi，j（t）+ pg，j（t））/2 为高斯分布的均值；σ2i，j（t）= |pi，j（t）- pi，j（t）|为高斯分布的标准差。

与标准PSO 算法相比，BBPSO 算法的最大优点就是无需设置惯性权重和学习因子等控制参数，更适合工程实际应用。

1.2 支持向量机

支持向量机是基于VC 维理论（Vapnik-Chervonenkis dimension）和结构风险最小化原则而提出的一种通用的机器学习算法[9]。其基本思想是寻找一个最优分类超平面，将两类样本尽可能正确地分开，并使分类间隔最大，进而获得较好的推广能力。

支持向量机最初是针对模式分类中线性可分的2 类分类问题提出的。给定大小为l 的训练集T={xi，yi}li=1，其中xi∈Rd是d 维的模式输入，yi∈{-1，1}是对应的期望输出，SVM 的目标是构造一个最优分类函数，尽可能多地正确划分样本且最大化分类间隔，即

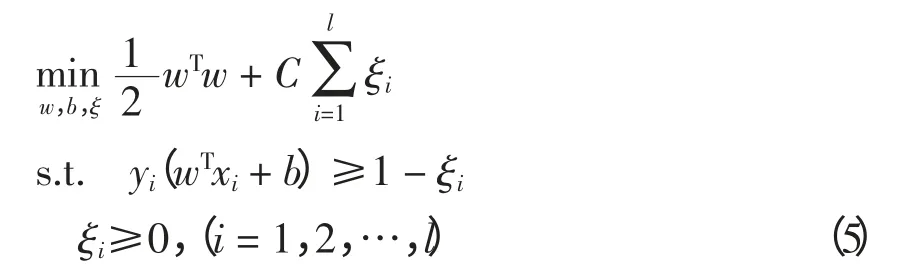
式中：C 为惩罚系数，ξi为松弛变量。此优化问题可根据拉格朗日方法转化为它的对偶形式为

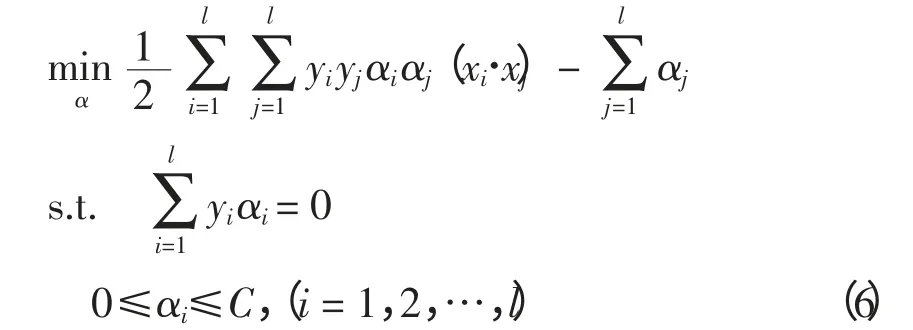
求解此凸二次规划问题，获得最优解α*=，选取位于开区间（0，C）中α*的分量，计算进而构造出最优分类函数为

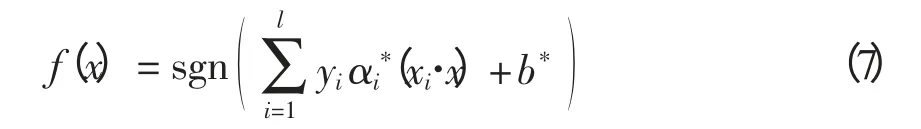
对于非线性问题，可以将输入空间的样本通过非线性变换Φ：Rd→H 映射到高维特征空间，从而转化为线性分类问题，形成非线性支持向量机。然而，SVM 并不直接求解特征空间的点积，而是利用原空间的核函数来代替它。根据泛函相关理论，只要核函数K（xi·xj）满足Mercer 条件，它就对应某一变换空间中的内积即K（xi·xj）=（Φ（xi）·Φ（xj））。此时最优分类函数改为

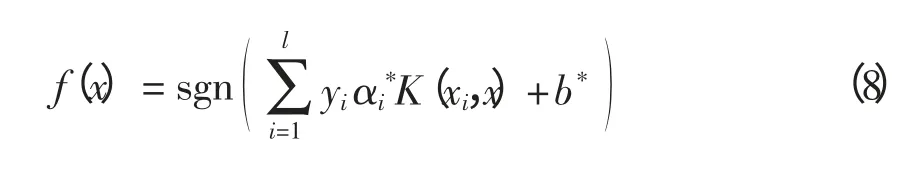
2 BBPSO 算法优化SVM 参数

支持向量机最重要的一个参数就是核函数，选择什么样的核函数就意味着训练样本映射到什么样的空间进行线性划分，会直接影响到分类性能。根据文献[10]的分析，对于线性不可分的小样本数据，选用径向基RBF（radial basis function）核函数时SVM 具有较高的性能。本文也选用RBF 作为核函数，该核函数形式为

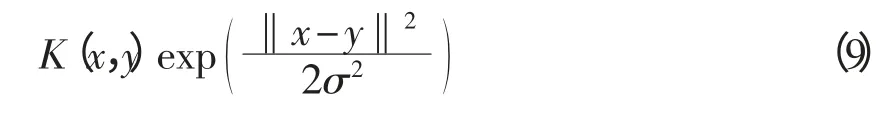
式中，参数σ 主要影响数据在特征空间中的分布，它会直接影响SVM 的泛化性能。式（5）中的惩罚系数C 在特征空间中确定经验水平并影响SVM 的推广能力。如果这两个参数选取不当，将会导致分类准确率直线下降。为此，本文采用了具有很强全局搜索能力的BBPSO 算法，对σ 和C 进行优化。并选择k-折交叉验证误差作为适应度函数，即

式中：li是对第i 个测试集进行测试时，错误分类的训练点个数；l 为训练集点数。k-折交叉验证的具体做法是：首先对预处理后的数据样本随机的分成k 个互不相交的子集S1，S2，…Sk，使每个子集的大小大致相等。然后进行k 次训练与测试。第i 次测试和训练的做法是：选择Si作为测试集，其余子集作为训练集，SVM 根据这个训练集求出决策函数后，对测试集Si进行测试，得到其中错误分类的训练点个数li，进而根据式（10）求出微粒的适应值。

BBPSO 算法优化SVM 参数的主要步骤如下：

步骤1 预处理训练集数据，主要是小波包特征提取和归一化处理。

步骤2 初始化微粒群中的微粒位置Pj（Cj，σj）、个体极值和全局极值；设置算法参数，种群规模、最大迭代代数等。

步骤3 计算每个微粒的适应值。

在蒸汽保护热处理的情况下，北美短叶松不一样的热处理时间得到了不一样的粗糙度数据和图片。由图3可知，在微观形貌上，热处理1 h样品上的碎片比未处理的少，故其粗糙度较低，但随着热处理时间的增加，木材表面出现了深而大的裂痕，同时碎片增多，故热处理2 h比热处理1 h粗糙，到了4 h时，样品形貌劈裂比未处理时更严重。而图片上2 h样品表面的碎片情况与未处理相比略少，故其粗糙度也比未处理的略低。

步骤4 更新微粒个体极值。

步骤5 更新种群全局极值。

步骤6 根据式（4）更新微粒位置。

步骤7 若满足停止条件（适应值误差小于设定阈值或迭代次数超过最大代数），搜索停止，输出全局最优位置和全局最优适应值。否则，返回步骤3 继续搜索。

3 基于BBPSO 优化SVM 的匝间短路故障诊断

本文所提故障诊断方法是通过建立状态识别/分类模型来实现的。首先对采样电流信号进行小波包分解，提取信号的故障特征，必要时作归一化处理，然后将预处理好的故障特征向量分为训练集和测试集。在训练过程中，采用SVM 拟合感应电机运行（完好或故障状态）时的状态模型，建立训练数据的最优决策超平面，针对SVM 中参数的选取，使用BBPSO 算法得到全局最优参数；训练完毕后，将测试集输入到SVM 中，判断最后的状态（完好或故障）结果，具体诊断模型如图1 所示。

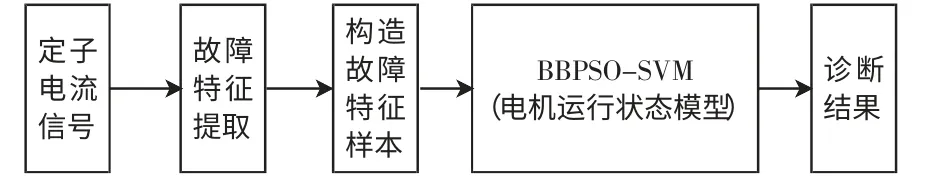
图1 感应电机定子匝间短路故障诊断模型Fig.1 Diagnosis model of stator winding inter-turn short circuit fault in induction motor

3.1 基于小波包的特征量提取

当电机定子绕组发生匝间短路故障时，三相绕组的对称性遭到破坏，呈现在气隙磁场中的是较强的空间谐波，定子电流中是较强的时间谐波（即高次谐波明显增强）。并且定子电流中的偶次谐波和奇次谐波也会因三相绕组失去对称性而有所增强。文献[11]，[12]指出：匝间短路故障的发生会使定子电流中出现特定的谐波分量或改变原某些谐波的能量。

上述与故障相关的谐波分量的出现或变化，必然引起信号相应频带能量的改变。由于小波包分解后的信号具有各个频带信号独立，能量守恒的特点，因此采用小波包对定子电流信号进行分解，提取匝间短路故障的特征。

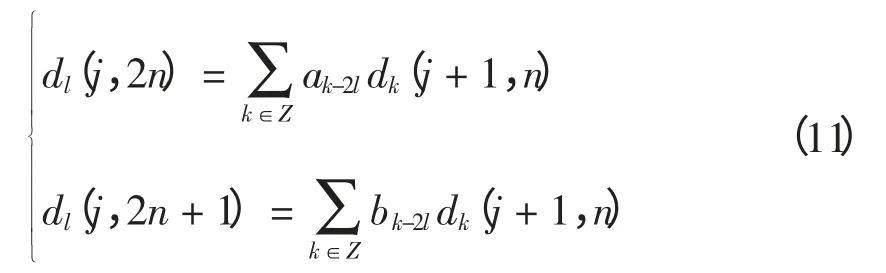
式中，ak-2l，bk-2l为小波包分解共轭滤波器系数。由Parseval 恒等式可知

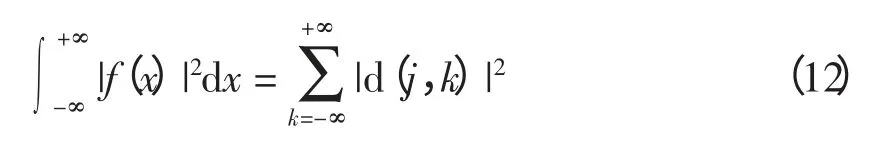
因此，小波包变换系数d（j，k）的平方具有能量的量纲，可直接用于信号的能量特征提取。

3.2 故障诊断步骤

骨干微粒群算法优化SVM 的感应电机定子故障诊断的具体步骤如下。

步骤1 对采样电流信号进行j 层小波包分解，得到M=2j个正交的频带。

步骤2 根据Parseval 定理，求取各个频带信号的能量Ei（i=1，2，…，M）。

式中，Ni为第i 个子频段的数据长度。

步骤3 构造状态特征向量，并进行归一化处理。

步骤4 选择T 作为SVM 的输入向量，并将特征向量样本分成训练集和测试集两部分，利用骨干微粒群算法和交叉检验优化支持向量机模型参数。

步骤5 利用最优模型参数和训练集构造SVM 分类器。

步骤6 利用训练得到的分类模型，对测试集进行诊断。

4 诊断实例分析

实验电机为Y132M-4 型感应电动机，其每相定子绕组210 匝。电机定子故障模拟方案如图2所示，通过改变短路电阻Rx的大小来模拟不同程度下的定子绕组匝间短路故障。

分别对定子有无故障（设置Rx=2 kΩ）状态下的电机进行试验。数据采集器以1 666 Hz 的速率进行8 000 个点的数据采集。在各状态条件下，对电机A 相电流进行21 组数据采集，本文仅列出各状态下的1 组信号，原始A 相电流信号如图3 所示。

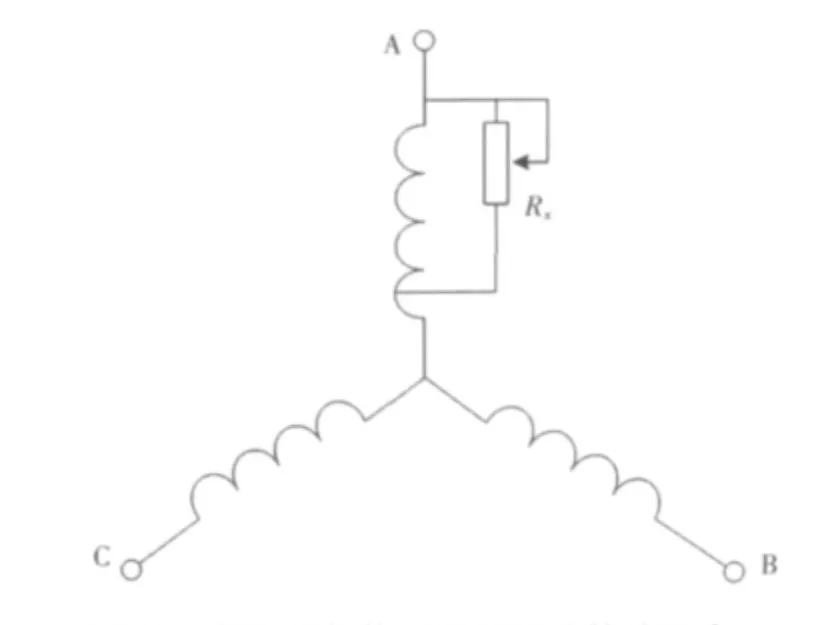
图2 定子A 相绕组匝间短路故障示意Fig.2 Stator A-phase winding inter-turn short circuit fault

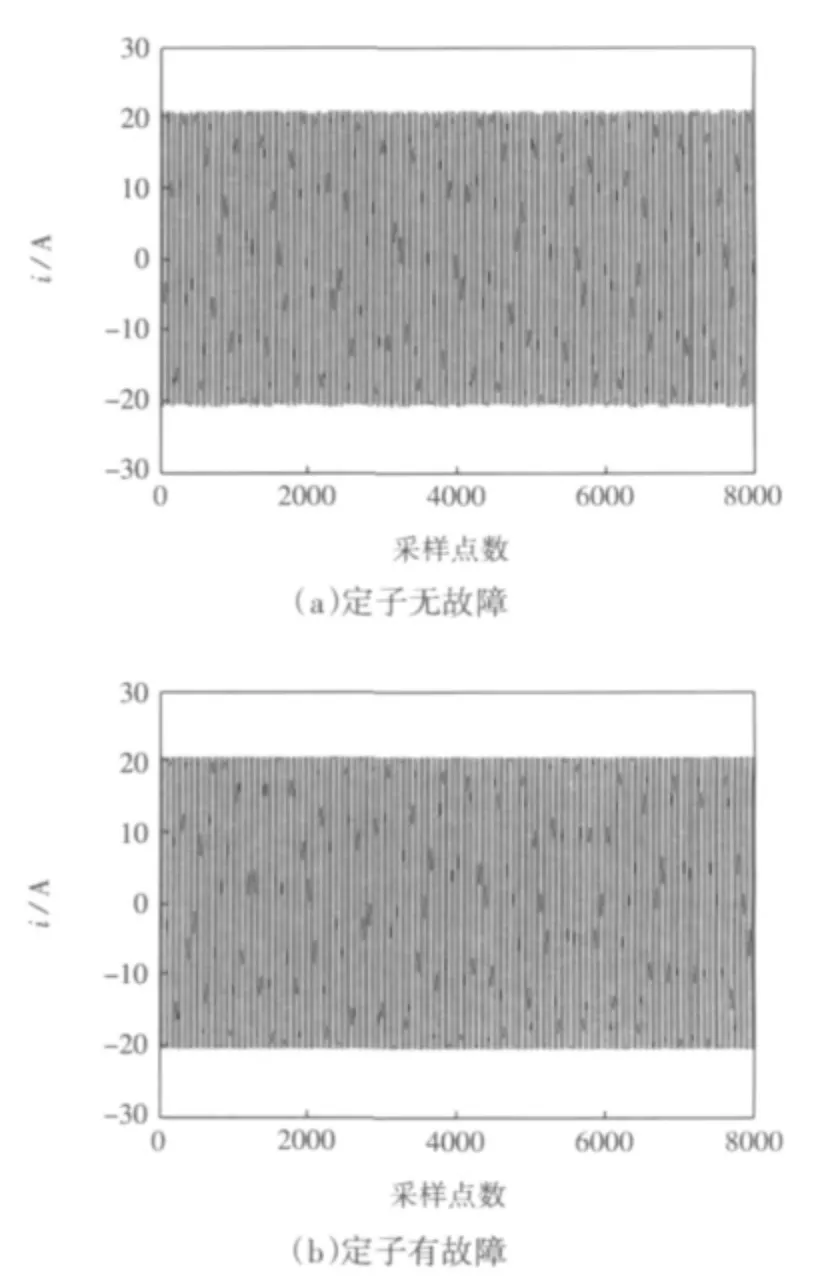
图3 定子电流信号波形Fig.3 Waveforms of stator current

对采样电流信号进行4 层Symlets 小波包分解，求取各频段信号的能量，并归一化。所列信号的特征向量如表1 所示。

表1 特征向量表Tab.1 Feature vectors

在本实验中，将各状态下的21×2 组数据进行分组，15×2 组作为训练集，6×2 组作为测试集。通过BBPSO 算法和k-折交叉检验在训练集上完成对SVM 模型参数的优化，其中参数k=3，BBPSO 的参数设置如表2 所示。

表2 BBPSO 算法参数设置Tab.2 Parameter configurations of the BBPSO

优化得到的最佳SVM 参数为Cbest= 3.016，σbest=1.648，3-折交叉验证误差为0.056。优化适应度曲线如图4 所示。

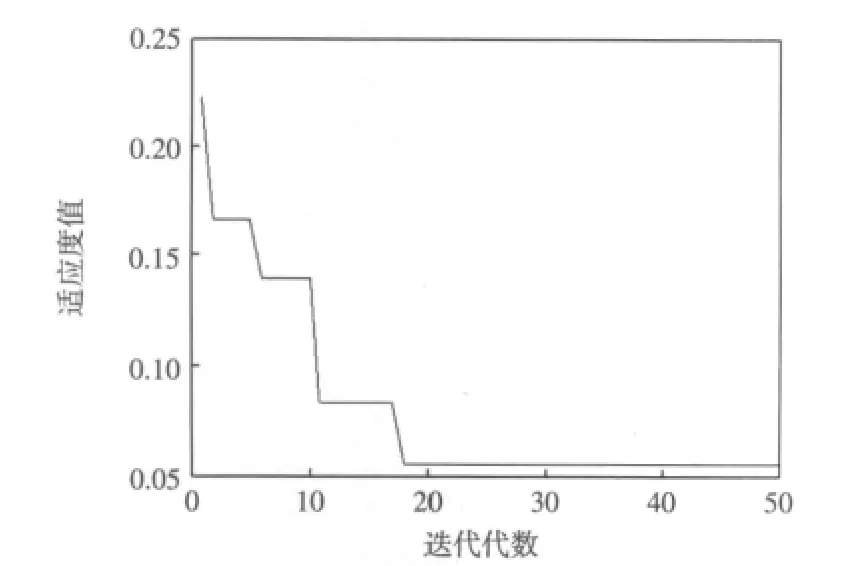
图4 适应度曲线Fig.4 Fitness evolutionary curve

利用训练集和最优参数Cbest和σbest对SVM 进行训练，形成故障诊断模型；然后对测试集进行分类，分类结果如表3 所示。感应电机的2 种状态，定子完好、定子匝间短路故障，对应的SVM 期望输出决策值分别为[SVM>0]和[SVM<0]。

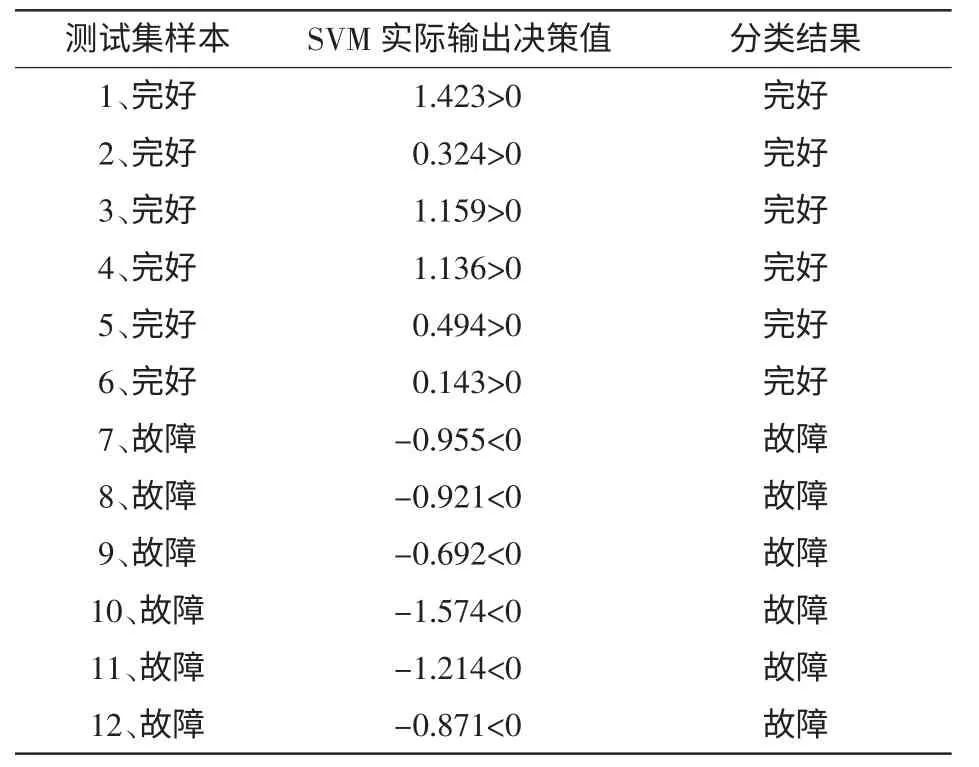
表3 支持向量机测试分类结果Tab.3 Test classification results of the SVM

从表3 可以看出，通过训练集和最优参数建立的感应电机匝间短路故障模型精度很高，在测试集上的识别准确率达到100%；同时也说明了该SVM 模型具有很好的推广性，尽管训练集只有30个数据样本，但是对测试集的识别准确率仍能达到100%。

为了验证最优SVM 模型参数的优越性，随机选取不同的C 和σ 值，在相同样本下进行识别试验比较，结果如表4 所示。

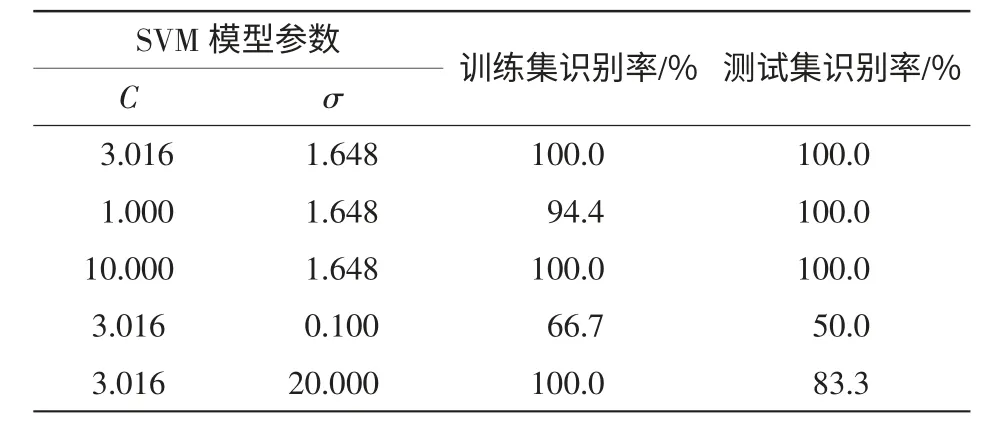
表4 不同模型参数的SVM 性能比较Tab.4 Comparison of SVM performance for different parameters

从表4 可以看出，过大或过小的C 和σ 值都会影响SVM 的识别性能。对于不同C 值下的SVM性能，虽然C=10.000 时训练集和测试集的识别率也能达到100%，但是过高的C 会导致过学习状态的发生。而通过BBPSO 算法获得的最优模型参数（第1 组数据）不但识别率最高，而且C 值较小，同时也克服了随机选择模型参数的盲目性，提高了模型的识别精度。

5 结语

本文首先提出一种基于BBPSO 算法的SVM参数优化方法，用以克服SVM 参数难以选择的问题，然后利用BBPSO 优化的SVM，来实现感应电机匝间短路故障诊断。试验结果表明，BBPSO 算法能够找出最优SVM 模型参数，并提高了识别模型的精度。在对试验电机的故障识别过程中，实例表明，该故障诊断方法具有很高的识别精度，即使在小样本情况下仍具有良好的推广能力。此外，该方法由于无需设置算法控制参数，因此更适合工程应用。

[1]Nandi S，Toliyat H A.Condition monitoring and fault diagnosis of electrical machines-a review [C]// IEEE Industry Applications Conference.Phoenix，USA：1999.

[2]宋功益，郭清滔，涂福荣，等（Song Gongyi，Guo Qingtao，Tu Furong，et al）. 模糊贝叶斯网的变压器故障诊断（Novel method for transformer faults diagnosis based on theory of fuzzy Bayesian networks）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：102-106.

[3]曲正伟，荣亚军，刘帅，等（Qu Zhengwei，Rong Yajun，Liu Shuai，et al）.RBF-NN 对发电机转子绕组匝间短路的诊断（RBF-NN’s diagnosis of generator rotor winding interturn short circuit fault）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：114-117.

[4]吕干云，程浩忠，董立新，等（Lü Ganyun，Chen Haozhong，Dong Lixin，et al）. 基于多级支持向量机分类器的电力变压器故障识别（Fault diagnosis of power transformer based on multi-layer SVM classifier）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（1）：19-22，52.

[5]朱苏航，吕干云（Zhu Suhang，Lü Ganyun）.利用遗传支持向量机进行电压暂降信号识别（Voltage sag signal identification with GA-SVM）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（1）：84-87.

[6]Kennedy J.Bare bones particle swarms [C]// IEEE Swarm Intelligence Symposium.Indianapolis，USA：2003.

[7]Kennedy J，Eberhart R.Particle swarm optimization [C]//International Conference on Neural Networks Proceedings.Perth，USA：1995.

[8]Clerc M，Kennedy J.The particle swarm-explosion，stability，and convergence in a multidimensional complex space[J].IEEE Trans on Evolutionary Computation，2002，6（1）：58-73.

[9]Cortes C，Vapnik V.Support-vector networks[J].MachineLearning，1995，20（3）：273-297.

[10]杨俊燕，张优云，赵荣珍（Yang Junyan，Zhang Youyun，Zhao Rongzhen）.支持向量机在机械设备振动信号趋势预测中的应用（Application of support vector machines in trend prediction of vibration signal of mechanical equipment）[J]. 西安交通大学学报（Journal of Xi’an Jiaotong University），2005，39（9）：950-953.

[11]Stavrou A，Sedding H G，Penman J.Current monitoring for detecting inter-turn short circuits in induction motors[J].IEEE Trans on Energy Conversion，2001，16（1）：32-37.

[12]Gentile G，Meo S，Ometto A.Induction motor current signature analysis to diagnostics of stator short circuits[C]//IEEE International Symposium on Diagnostics for Electric Machines，Power Electronics and Drives. Atlanta，USA：2003.