周期均值叠加法在中长期预报中的应用
2013-02-28张青山任海青
张青山,任海青,张 宁
(辽宁省水文水资源勘测局丹东分局,辽宁 丹东 118001)
1 爱河流域概况
爱河是鸭绿江下游水丰水库以下最大支流,也是丹东地区的较大主要河流,发源于宽甸县双山子乡盘道岭,流域面积5891 km2,河长189 km,流经凤城市、振安区、宽甸县于丹东市振安区九连城注入鸭绿江。流域内地势西北高,东南低,山地占77%,丘陵占17%。该流域植被良好,包气带不厚,地下水埋藏较浅。梨树沟水文站是爱河下游控制站,流域面积5629 km2,河长为165 km,距丹东潮水位站35 km,该站自1956年开始已有50余年完整的流量实测资料。流域内建有雨量站20处,其中草河站以上8处,龙湾站以上5处;铁佛寺站以上5处,区间有民生、梨树沟2处。该站1960年8月4日发生有资料记载以来的最大洪水,洪峰流量为17400 m3/s,为有资料记载以来第一大洪水;2010年8月20日18时该站发生12300 m3/s洪峰流量,相应水位101.75 m,为有资料记载以来第二大洪水。爱河流域历来是丹东地区防汛重点地区,尤其是下游,关系着马市、丹东市城区近百万人口生命财产的安全问题,多年来已引起各级领导的关注,该流域的洪水预报就显得尤为重要。
2 中长期预报的思路和方法
2.1 基本思路
概率统计的方法越来越多地应用于水文预报工作中,其基本原则是从大量的历史资料中应用数理统计的方法去寻求分析水文要素历史变化的统计规律以及与其他因素的关系,然后用这些规律来进行洪水预报。本文是采用周期均值叠加方法分析梨树沟站多年最大洪峰流量的统计规律,并利用周期均值外推后叠加做出洪水预报。
2.2 周期均值叠加法应用分析过程
选用的分析因子是年最大流量,即把梨树沟站逐年年最大流量的变化过程作为一个波动过程看待,并认为这个波动是有n个具有不同周期的周期波叠加形成的,其数学模型为

式中:X(t)为年最大流量序列;pi(t)为各个周期波序列;ε(t)为各个误差项序列。只要根据实测的历年最大洪峰流量数据,分析识别出年最大流量所含有的周期,而且这些周期在预测期内仍然保持不变的话,就可以根据分析出来的周期分别进行外延,然后再叠加起来进行洪峰预报。由于年洪峰流量过程线的外形比较复杂,在图形外观很难判断出他是否存在周期,存在的周期是多少,周期的可靠性如何,为解决这些问题本文是采用方差分析法来分析识别周期。
选取梨树沟站1956—2006年51年最大洪峰流量资料进行分析,其过程如下:
各年最大流量距平值△Qi及△Qi2:△Qi=Qi-;
计算周期 k 的最大值:k=(资料序列数-1)/2=(51-1)/2=25,最大周期可定为 25 年。初步选定了 25,21,19,17,15,12,11,9 共 8 个周期进行试验分析。
由上述资料分别列表计算各实验周期的基本数据(表1为12年周期计算表),并分别计算每个试验周期的组间离差平方和S1、组内离差平方和S2、组间自由度f1和组内自由度f2、组间方差S1/f1与组内方差S2/f2、方差比F、选定信度0.10,根据自由度f1,f2在 F分布表中查处相应F0.10数据,各计算参数如表2。
比较确定是否有周期,若 F>F0.10说明有周期存在,从表2中数据看出19,17年周期 F<F0.10说明无周期或周期信度较低,其余周期信度在90%以上。从中选取 F值较大的周期为第一周期,根据丹东地区历史资料情况选取12年周期作为第一周期,并计算每组平均值作为周期波中各年的振幅值,过滤该振幅值构成新序列X1(t)。根据新序列X1(t)的数据,用分析第一周期的各个步骤来分析第二周期的新序列X2(t)。以此类推分别试验推算25,15,11,9,21作为第2~6周期,并计算出各周期振幅值,每计算完一个周期进行一次叠加比较拟合值与实测值拟合情况,否则再按上述步骤继续分析,直到满意为止。
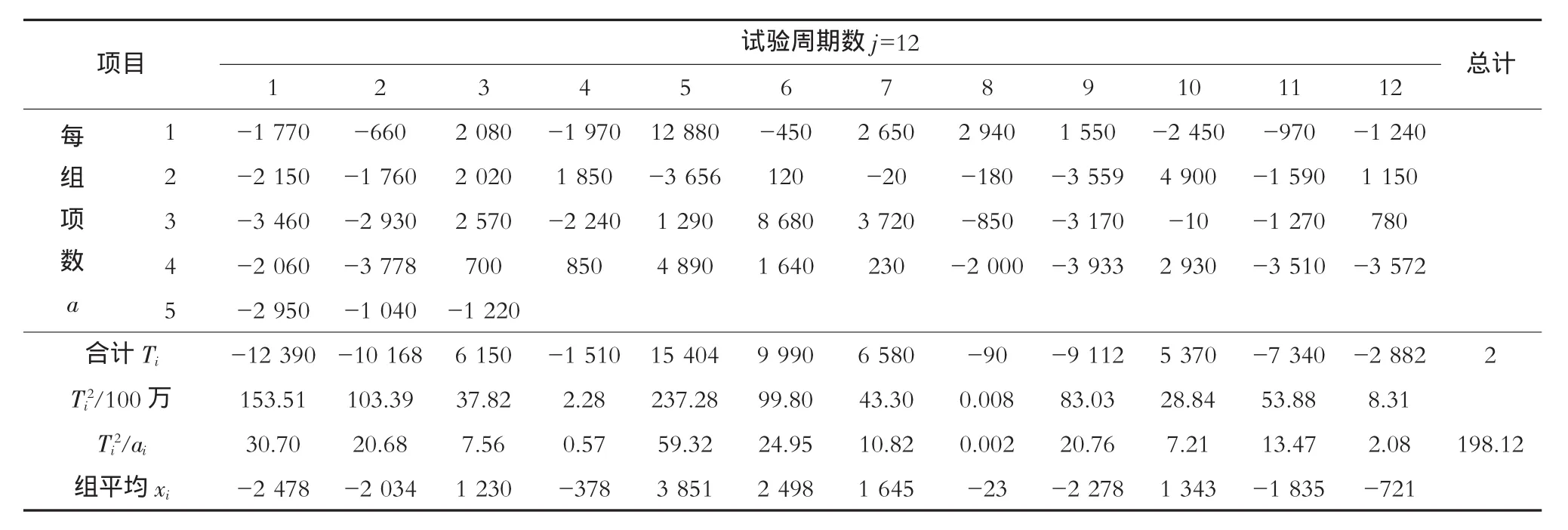
表1 实验周期分组排列表

表2 各种试验周期的方差比F数值表
应用上述周期波序列叠加后的拟合流量,与原实测洪峰流量进行比较,可见二者相差不大,拟合很好,应用周期波叠加的过程线与实测过程线的比较见图1。
预报时只需在计算表中把各个周期波数值外推一行,把这些数据叠加起来再加上多年实测平均Q值得到的数据即为预报值。
3 预报实例
近些年来已把周期值叠加法应用到爱河梨树沟站的中长期预报中,精度是较高的,表3例举了2010、2012两年的预报过程及结果(其他年份洪水较小)。2010年拟合流量12400 m3/s,实测流量 12300 m3/s,误差-100 m3/s;2012年拟合流量4850 m3/s,实测流量4870 m3/s,误差 20.0 m3/s。
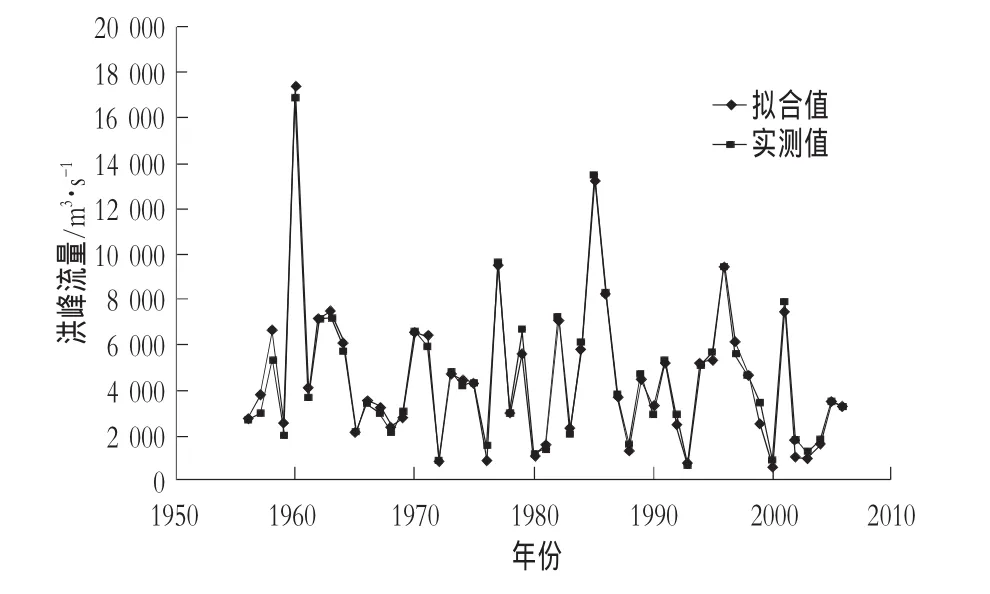
图1 周期均值叠加法预报流量拟合图
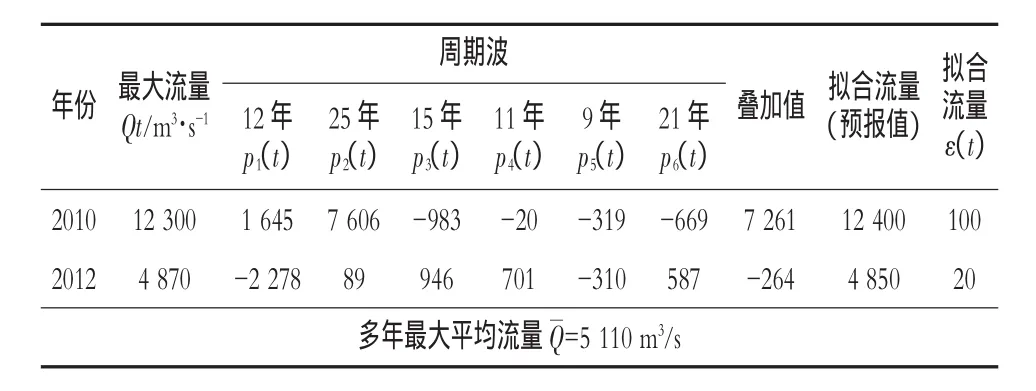
表3 爱河梨树沟站周期值叠加法预报实例表
4 结语
1)周期值叠加法进行梨树沟站中长期预报,其方法是可行的,精度也很高。
2)应用方差分析来识别周期,其方法比较简单。但由于水文要素很难满足每组数据符合正态分布及各组总体的均方差相等的条件,因此所得到的分析结果应该是近似的。
3)为防止出现伪周期现象,在用方差分析来识别周期时其信度标准不要太低,一般不要低于0.10。
4)应用方差分析得到的周期用于洪水预报时,要及时根据实测资料检验周期的稳定性,若发现周期有显著的波动,在预报时不宜再应用这种周期进行外延。
