基于应力恢复子模型的车身结构计算方法研究

周 泽 李光耀 成艾国 赵 敏

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

子模型技术无外部节点数量的限制，适合于整体框架结构分析中需要获取局部细节精确解的问题，相比子结构技术具有更好的适用性，因而在工程问题中得到了广泛的应用。如文献［1］运用子模型技术进行平板裂纹区域应力研究，获得了局部精确应力解；文献［2］运用子模型技术对车轮疲劳寿命进行研究，获得了列车轮毂的精确接触应力；文献［3］运用子模型技术进行局部模型的流固耦合求解，获得了精确的计算结果；文献［4］运用子模型方法对大桥局部结构进行屈曲研究，其子模型计算结果与测试值基本一致；文献［5］运用子模型技术对微观结构进行分析，获得了应力分布的精确结果；文献［6］将子模型方法运用于口腔医学研究，取得了陶瓷牙齿裂纹研究方面的成果；文献［7］运用子模型方法进行桥面结构研究，验证了桥面基础弯沉问题；文献［8］在跨悬索桥结构研究中，采用子模型技术获得的结构关键位置应力与实测值一致；文献［9］运用子模型技术对斜拉桥的局部力学行为进行研究，确保了局部应力与实测值的一致性。上述的研究均表明：子模型法在保证计算效率的同时，能获取结构关键部位的详细信息，且计算结果具有很高的精度，是进行整车结构中局部精细应力分析的有效方法。

目前，子模型技术主要侧重于研究位移边界方法［1－9］。本文将应力恢复边界［10］的子模型方法（recovery based stress method，RSM）应用于汽车车身结构的计算与分析，有效提高了车身结构的计算精度和分析效率，证明其方法适用于工程实际应用。

1 子模型技术

1.1 子模型分析流程

典型子模型分析流程如图1所示。首先，对全局模型进行线性数值计算，并根据计算结果择取所关注区域边界节点的位移边界。通过应力恢复的子模型方法获得在全局模型中该局部区域的边界节点载荷；然后通过MATLAB编程，将全局模型中的边界节点载荷根据形函数进行插值计算，获得新边界节点载荷，并以此边界条件进行子模型构建。

在细化子模型网格后，采用同样方法，重新获得新网格尺寸下的子模型边界节点载荷条件。逐步细化子模型网格，直到有限元模型数值解关于网格尺寸收敛，该数值解即为结构分析精确数值解。

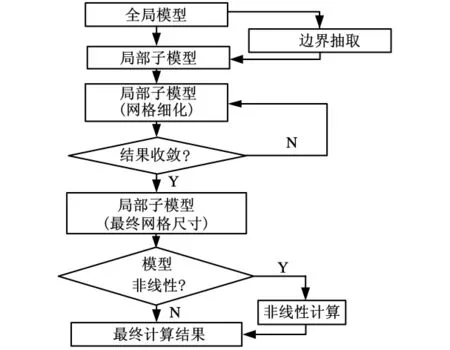
图1 子模型分析流程图

1.2 基于应力恢复的子模型方法

一般而言，位移边界及载荷边界获取是通过保留初始模型边界网格，并在子模型与初始模型边界网格之间采用粗细网格过渡方法实现的，如图2所示。图3所示为位移/载荷边界方法网格边界处理示意图。

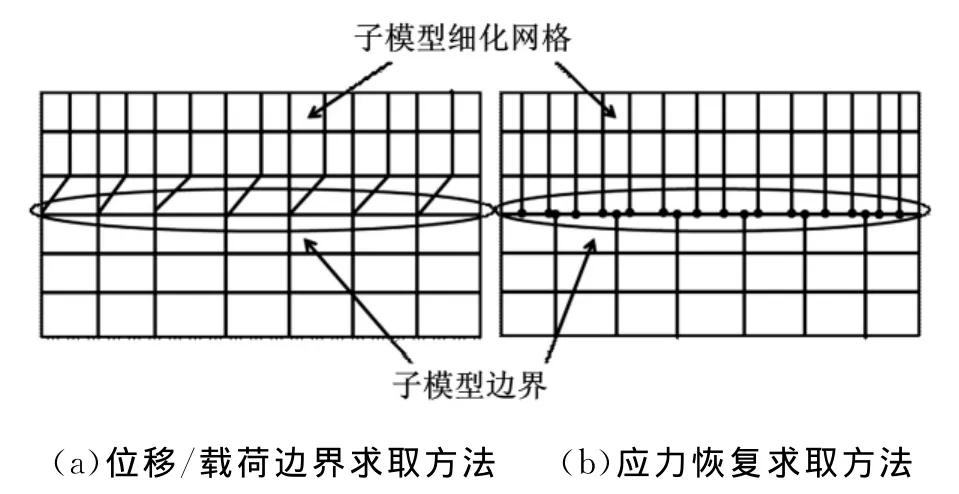
图2 子模型细化网格后的边界求取方法

基于应力恢复子模型边界获取方法能避免网格细化带来的边界处理繁杂及减少网格剧增带来的网格处理工作量，提高网格过渡区域的网格质量和计算效率。恢复应力的子模型边界载荷可以表示为

式中，Sp为恢复应力多项式；n为边界法向量。

图3 位移/载荷边界方法网格边界处理示意图

随着后续网格的进一步细化，在子模型边界Γ区域，将模型边界节点力值通过有限元型函数重新插值到新边界节点上（图2b），即可获得新边界节点的载荷边界条件。新的子模型边界节点载荷＾f可表示为

式中，t为单元厚度；N为型函数。

2 车身结构分析现状及方法

典型车身结构强度的主要分析流程为：首先测试或计算出典型行驶工况［11－12］（如制动、转向、扭转、过坑等）中底盘与车身连接点（即底盘安装硬点）处的力和力矩；然后将其施加至车身有限元模型，并通过惯性释放的方法计算出白车身相关区域的应力值。

本文通过道路耐久性试验测试获得的整车各行驶工况的加速度值、典型整车强度工况和应力判断标准如表1所示。表1中，根据各工况在整车道路耐久性试验中出现的频率情况分为峰值工况和极限工况，出现频率较高的工况为峰值工况，而出现次数较少的工况为极限工况。

表1 典型整车强度工况及应力判断标准

根据表1各工况加速度值和整车动力学可计算获得整车底盘与车身连接点处的载荷。整车动力学模型如图4所示。

将计算所得底盘安装点处载荷施加在白车身有限元模型上，即可获得白车身各工况下的应力情况，根据表1中各工况的应力判断标准，即可找出各耐久性路试车身的开裂问题，并提出相应优化方案。

图4 整车强度工况计算模型

3 计算案例

在某型号微型车耐久性试验中，尾门框上角区域出现长约30mm裂纹（图5），且该处几何形状较为复杂，最小圆角约为2mm，同时该裂纹距离圆角边界约20mm。而通常计算的10mm网格有限元模型将忽略该局部重要特征，这一忽略，特别是区域圆角特征的忽略，将直接导致数值计算精度的低下和计算收敛性条件难以满足，因此必须针对该区域进行网格精细化计算。本文使用基于应力恢复的边界子模型方法来获取上述局部区域载荷条件下的精确解。

图5 某车型尾门框裂纹与几何模型

3.1 整车有限元模型及其验证

图6 整车模型

整车有限元模型如图6所示，其网格尺寸为10mm，总共有节点672 118个、单元641 852个，模型总质量为1680kg。整车实际满载质量为1800kg，其中底盘件约为140kg。车身有限元模型单元为壳单元，焊点单元为CWELD单元，主要附件质量采用点质量MASS单元，其数值均为实测值。有限元计算软件为MSC.Nastran，白车身主要性能指标的试验及仿真值对比如表2所示，因表中各仿真指标误差控制在5%以内，故满足计算精度要求。

表2 整车性能指标试验及仿真对比

3.2 整车模型及子模型计算结果

整车结果表明：在过坑扭转工况时，开裂位置单元应力值为326.6MPa，且为该局部区域应力值最大处。该处的零件材料为B170P，理论屈服值为170～260MPa，抗拉极限大于340MPa。根据表1中的过坑扭转工况定义，该处应力值符合强度工况要求，路试开裂风险较小，因而需要进一步研究开裂原因。

图7 有限元子模型

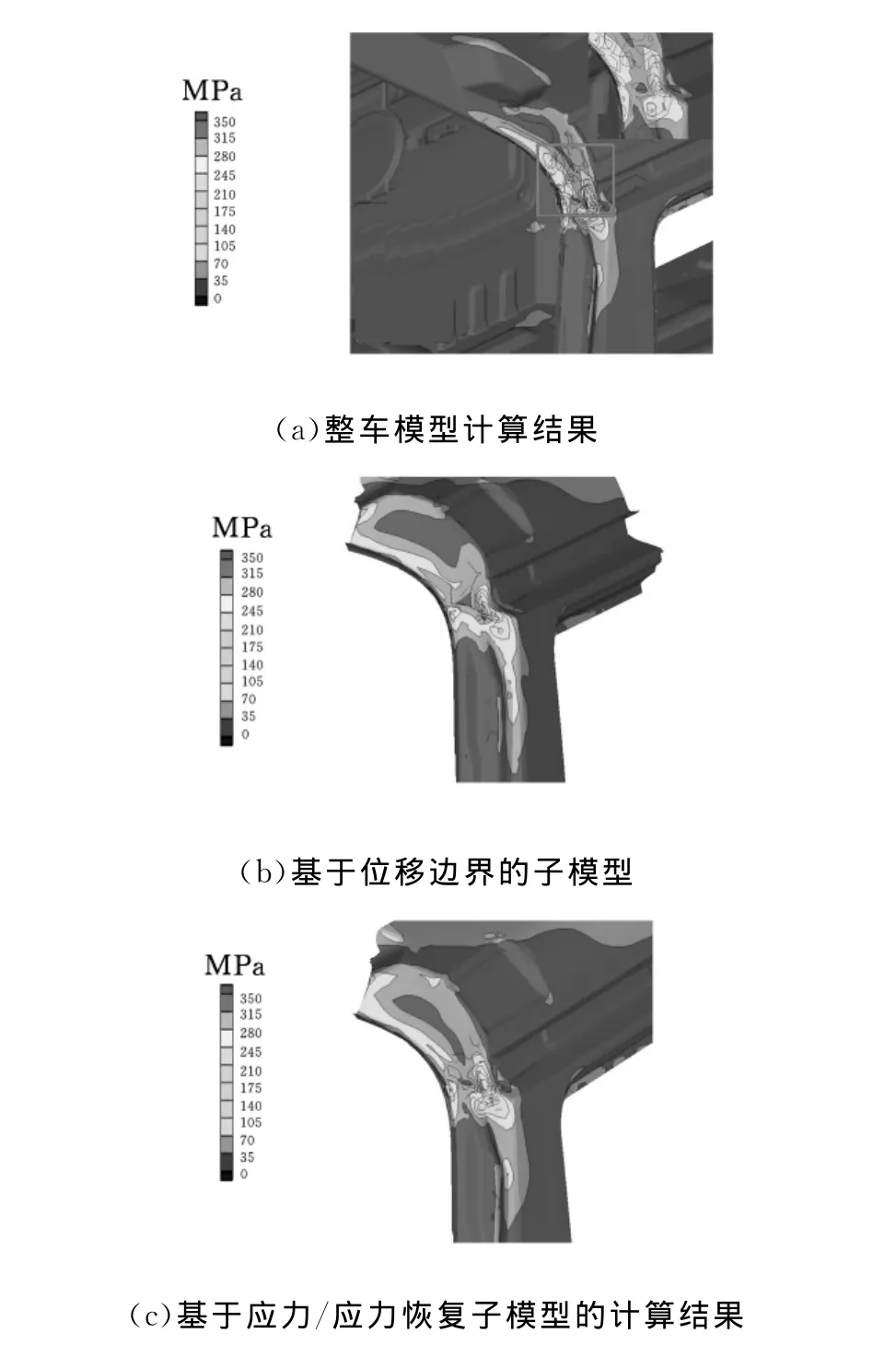
图8 整车模型及子模型计算结果对比

在局部子模型（图7）中，应选择距离裂纹位置足够远的节点。本文中选择距离裂纹位置400mm处作为子模型的边界。该位置应力值较小，且应力梯度变化小。如图8所示，基于位移边界子模型开裂位置应力值σ为327.2MPa，而基于应力边界子模型开裂位置应力值为326.6MPa，基于应力恢复子模型在局部网格未细化时的结果与基于应力边界子模型的结果一致，三种子模型处理技术均满足精度要求。随着子模型网格细化程度的增加，若采用基于位移/载荷边界方法将导致初始的边界网格与细化网格子模型之间的过渡过于复杂，会导致子模型网格工作量急剧增大，同时计算不确定性增大（图3）。故本文采用基于应力恢复子模型方法进行网格细化处理。

3.3 子模型收敛性计算

在上述子模型基础上，逐步细化网格尺寸，直到满足网格尺寸收敛性要求。图9为不同网格尺寸下的局部开裂区域应力云图，根据计算结果可知，随着网格逐步细化，开裂区域的应力云图会更加圆滑，更加合理。在网格尺寸分别为2mm、1mm时，两者的应力云图差别不大，接近一致。由图10、图11所示可知，随着网格逐步细化，结构应力值逐步增大而应变能误差逐步减小，在网格尺寸小于2mm后，变化趋于平缓。其中，应变能误差根据网格尺寸0.5mm子模型与各网格尺寸子模型的总应变能差值进行评估。网格尺寸为0.5mm的子模型，其节点数量约为184 000个。其他网格尺寸子模型节点数量如表3所示。

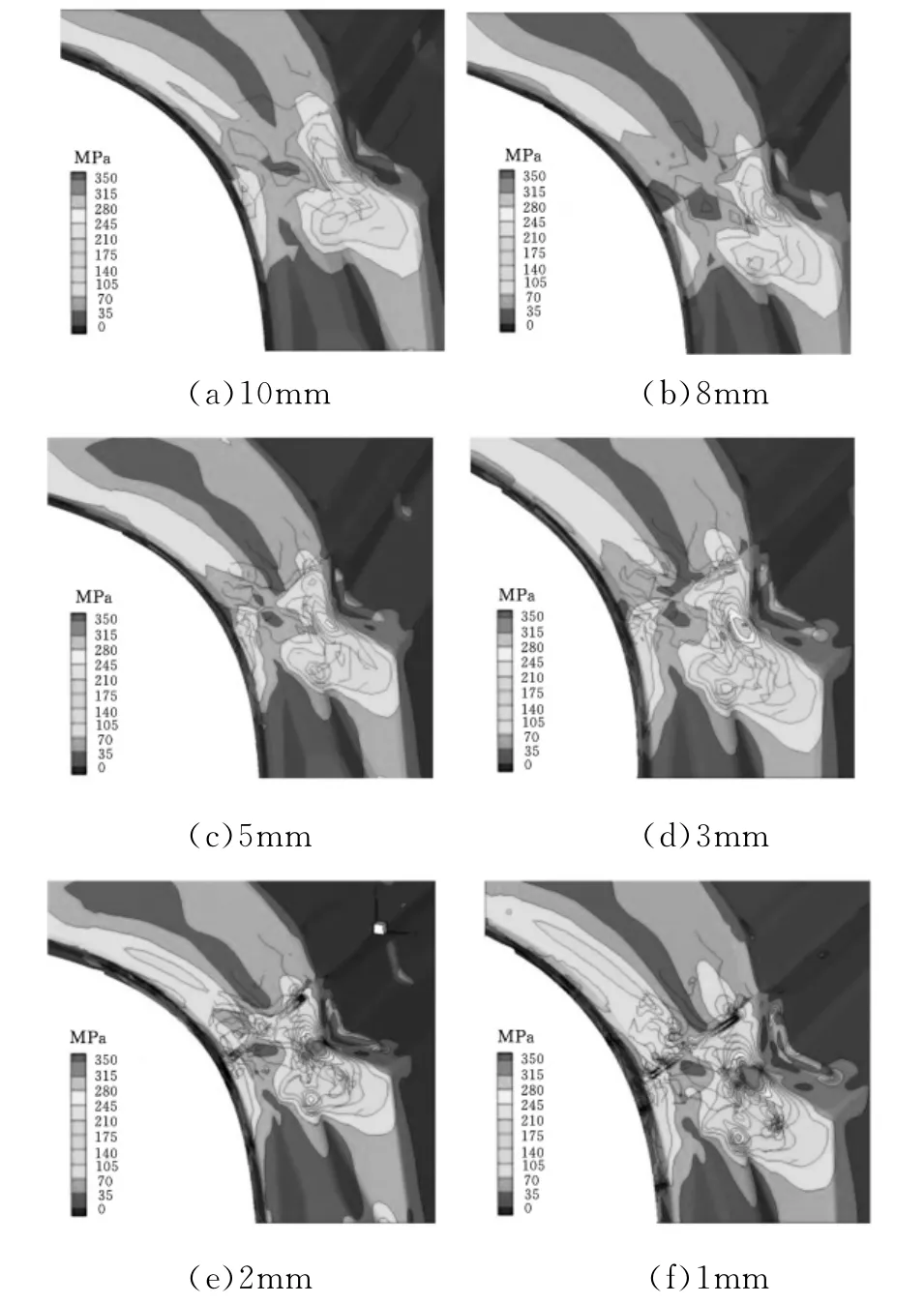
图9 不同网格尺寸下的局部开裂区域应力云图

图10 网格尺寸与开裂处应力值

图11 网格尺寸与部件应变能误差

表3 模型尺寸与计算时间对比

因此，在网格尺寸为2mm时，该模型数值计算结果满足网格尺寸收敛性要求。故分析该局部结构时，要求其网格尺寸至少不大于2mm。而作为指导结构设计的CAE工程师，应在此子模型计算结果的基础上，提供改进和优化建议。

上述整车模型及子模型计算均在商业有限元软件MSC.Nastran中进行。计算表明：当整车模型采用2mm网格时，整车模型节点数量预计约为16 802 950（约为10mm网格模型的25倍），根据文献［13］经验，该节点数量模型无法在单台服务器上计算，只能采用分布式计算器求解。而子模型随着网格的逐步细分，模型计算的时间仍然较短，即使将网格划分为1mm的子模型，在节点数量高达442 193时，其计算时间也仅为893.347s，计算花费增加不多（表3）。因此，基于计算精度及计算资源消耗均衡考虑，子模型是提高车身结构分析精度的合适选择。

4 结语

对于车身结构而言，特别是门框接头等主要受力件，是整车受力结构的重要组成部分，也是其破坏的潜在区域，因而有必要获得局部区域应力值。本文基于整车框架结构考虑，采用基于应力恢复的车身计算方法获得其关键受力区域的精确解，极大地提高了计算的精度和求解的效率。另外，本文介绍的基于应力恢复的子模型方法，不局限于车身结构分析，适用于整体受力框架需要获得局部精确数值解的问题，具有普遍的工程适用性。

［1］ Kwon S W，Sun S T.Characteristics of Three－dimensional Stress Fields in Plates with a Throughthe－thickness Crack［J］.International Journal of Fracture，2000，104：291－315.

［2］ Liu Yongming，Stratman B，Mahadevan S.Fatigue Crack Initiation Llife Prediction of Railroad Wheels［J］.International Journal of Fatigue，2006，28：747－756.

［3］ Michael L，Steven P A，Eugene K，et al.A Finite Element Model Predicts the Mechanotransduction Response of Tendon Cells to Cyclic Tensile Loading［J］.Biomech Model Mechanobiol，2008，7：405－416.

［4］ Wang Hao，Li A Q，Guo T，et al.Accurate Stress A－nalysis on Rigid Central Bckle of Long－span Suspension Bridges Based on Submodel Method［J］.Science in China Series E：Technological Science，2009，54（4）：1019－1026.

［5］ Johar C，Kirsten W Z，Oliver A.Investigation of Stress Distribution in via Bottom of Cu－via Structures with Different［J］.Microelectronics Reliability，2009，49：1090－1095.

［6］ Liu Hengliang，Lin C L，Sun M T，et al.3DMicrocrack Propagation Simulation at Enamel/Adhesive Interface Using FE Submodeling and Element Death Techniques via form by Means of Submodeling［J］.Annals of Biomedical Engin Eering.2010，38：2004－2012.

［7］ 徐伟，李智，张肖宁.子模型法在大跨径斜拉桥桥面结构分析中的应用［J］.土木工程学报，2004，37（6）：30－34.Xu Wei，Li Zhi，Zhang Xiaoning.Application of Submodeling Method for Deck Structure of Diagonal Cable－stayed Bridge with Long Span［J］.China Civil Engineering Joural，2004，37（6）：30－34.

［8］ 李爱群，王浩.子模型法在超大跨悬索桥钢箱梁应力分析中的应用［J］.工程力学，2007，24（2）：80－84.Li Aiqun，Wang Hao.Stress Analysis on Steel Box Girders of Super－long－span Suspension Bridges with Submodel Method［J］.Engineering Mechanics，2007，24（2）：80－84.

［9］ 张鹏飞，张启伟.千米级斜拉桥扁平钢箱梁的局部力学行为［J］.天津大学学报，2010，43（7）：593－600.Zhang Pengfei，Zhang Qiwei.Local Mechanical Behavior of Flat Steel Box Girder for Kilometer Level Cable Stayed Bridge［J］.Journal of Tianjin University，2010，43（7）：593－600.

［10］ Gu H，Zong Z，Hung K C.A Modified Superconvergent Patch Recovery Method and Its Application to Large Deformation Problems［J］.Finite Elements in Analysis and Design，2004，40：665－687.

［11］ Heisler H.Advanced Vehicle Techolgy［M］.Oxford：Reed Educational and Professional Publishing Ltd，Second Editional.2002.

［12］ 汽车工程手册编辑委员会.汽车工程手册［M］.北京：人民交通出版社，2001.

［13］ MSC.Software Corporation.MD.Nastran Installation and Operations Guide［M］.Santa Ana：MSC.Software Corporation，2008.