数值建模时骨料对混凝土侵彻及毁伤问题的影响＊

张凤国，刘 军，梁龙河，楼建锋，王 政

（北京应用物理与计算数学研究所，北京100094）

早期对混凝土冲击响应的数值模拟主要将混凝土靶板作为均匀连续介质处理，实际上混凝土材料是由砂浆和骨料等介质混合而成，显然，连续介质模型不能描述混凝土细观非均匀性对于材料损伤及破坏局部化的影响。A.Vervuurt等［1］应用网格模型模拟混凝土的破坏过程，假定混凝土为砂浆基质、骨料和粘接剂组成三相复合材料，首先根据一定的骨料粒径分布，随机生成混凝土的三相结构，然后把规则或不规则的三角形网格映射到生成的混凝土的三相结构上，对于分别处于不同相中的单元赋予对应的力学性质参数，以反映混凝土细观层次上的非均匀性。

一些学者进行了类似的研究，如刘光廷等［2］根据混凝土骨料的级配生成混凝土结构（考虑了骨料分布的随机性），并将有限元网格投影到该结构上，根据不同类型单元的位置确定单元的材料特性，用以代表混凝土的三相结构，采用非线性有限元技术模拟了混凝土单边裂缝受拉试件从损伤到断裂的全过程。混凝土材料的宏观力学特性根据不同相材料所占的体积份额给出。显然，采用多相数值计算模型，提高了混凝土冲击响应的数值模拟技术水平［3］。

尽管如此，由于含骨料混凝土数值建模在程序处理上相对比较复杂，混凝土各相材料参数还不是十分完备，以及各相之间相互作用的数值处理和物理描述也有待进一步完善，目前混凝土的数值建模还主要是以素混凝土建模为主，即将混凝土靶板作为均匀连续介质处理。

本文中，拟采用数值方法分析含骨料混凝土的数值建模对混凝土侵彻及毁伤问题的影响，分析结果可为相关混凝土数值模拟问题的计算分析提供参考。

1 含骨料混凝土的数值建模

含骨料混凝土结构一般都采用均匀搅拌的工程方法浇筑而成，选取的骨料尺寸分布范围也不大，在此条件下，基于均匀分布的思想，利用单元置换的方法，我们在二维拉格朗日有限元程序LTZ－2D 中实现了含骨料混凝土靶材料的数值建模。LTZ－2D 程序采用的是三角形结构单元，相邻的2个三角形单元可以组成1个四边形单元，单元置换方法首先建立砂浆材料的数值模型，然后每相隔一定的四边形单元将单元的砂浆材料参数置换成骨料的材料参数，从而建立含骨料混凝土材料的数值模型。图1显示了含不同比例骨料混凝土的数值模型。

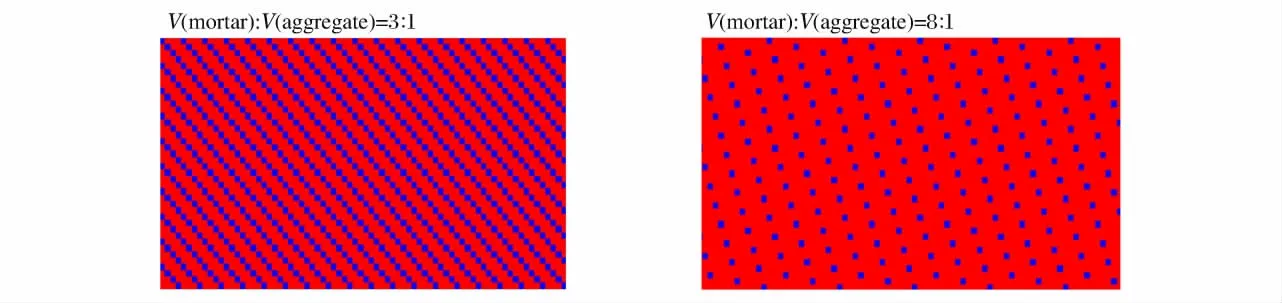
图1 含不同比例的骨料混凝土数值模型Fig.1 Computing models of concrete targets with different aggregate structure

2 混凝土各相材料的物理描述

混凝土结构由不同材料混合而成，在弹性－声波加载范围内对不同材料之间定量上的耦合关系可以进行描述。R.Hill［4］给出了弹性范围内不同物质混合的一般描述，即混凝土各相材料与其等效混凝土材料之间的力学表达式，在假设应力相同条件下给出了混合物的计算公式

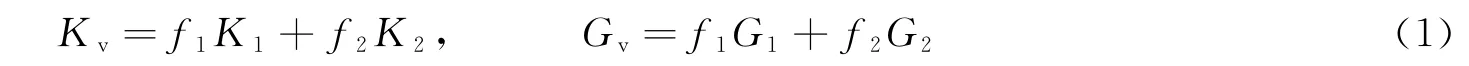
在假设应变相同条件下给出了计算公式

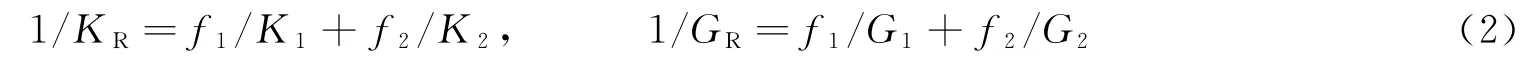
式中：下标i＝1，2表示各相材料，fi为材料所占份额，且∑fi＝1，K 为材料的体积模量，G 为材料的剪切模量。

同时，若基于应力应变关系，则可以推导出近似关系式

本文中将混凝土作为砂浆和骨料两相材料处理，根据公式（2），可以由各相材料的抗压强度fc，i 和密度ρi 得到等效混凝土材料的抗压强度fc和密度ρ 分别为

3 含骨料混凝土侵彻问题的数值分析

数值计算时选取的骨料的抗压强度为154 MPa，密度为2.66g／cm3，压实强度为105 MPa，对应的体积应变为0.008 77，砂浆的抗压强度为48MPa，密度为2.44g／cm3。为了对比分析含骨料混凝土的数值建模对混凝土侵彻及毁伤问题的影响，将含骨料混凝土等效为素混凝土，砂浆和骨料的体积比为3∶1，并根据公式（4）～（5）得到等效混凝土的抗压强度为58MPa，密度为2.495g／cm3，计算时采用的压实强度为1.209GPa，对应的体积应变为0.167 05。骨料、砂浆及等效混凝土的状态方程均采用改进后的混凝土HJC模型［5］，其他模型参数和材料参数可以根据文献给出的方法确定［6－7］。损伤模型采用文献中给出的混凝土动态拉伸损伤模型及参数［8］。数值模拟利用二维Lagrange弹塑性流体力学有限元程序LTZ－2D，弹体质量0.5kg，弹体直径25.4mm，弹头曲率半径与弹体直径之比为3.0，混凝土薄靶厚178mm、厚靶厚1m。

图2 含骨料混凝土靶以及均匀素混凝土靶侵彻后的损伤情况Fig.2 The damage graphs of concrete targets as the penetration results

图2 显示了弹体以500m／s速度贯穿混凝土薄靶后的数值模拟结果（密度图）。计算结果表明，弹体对含骨料混凝土薄靶造成的损伤破坏面积大于等效混凝土靶，且靶板的破坏主要沿着骨料界面产生和发展，即由于骨料的存在，增加了混凝土内部裂纹的扩展范围，加快了裂纹的扩展速度。同时，不同撞击速度vi下弹体剩余速度vr的对比结果（见图3）显示，低速侵彻时，骨料对弹体的侵彻有一定的阻碍作用，弹体剩余速度低于等效混凝土的计算结果，而较高速侵彻情况下，由于靶板背面的损伤破坏情况增大，对弹体在最后侵彻过程的阻碍作用减小，因而弹体剩余速度高于等效混凝土的计算结果。

由于靶板背面脱落情况的存在，弹体对混凝土厚靶的侵彻有别于薄靶情况。对于厚靶的侵彻情况，我们分析了弹体的速度v 和位移d 随时间的变化情况，如图4所示。相对于等效混凝土靶，由于骨料的存在，弹体在侵彻过程中的速度波动相对大一些，但在整个侵彻过程中，含骨料混凝土的数值建模对弹体的侵彻过程影响不大，主要影响也是在弹体速度降为较低的时候，因而含骨料混凝土计算的弹体侵彻深度较大，但总体差别不大。同时，计算结果也验证了我们所采用的混凝土等效处理方法的适用性、所选用的模型参数和材料参数的合理性。

不过，这里需要说明的是，对于弹体的侵彻，骨料的影响是相对的。一般情况下，就局部而言骨料尺寸相对弹体尺寸较小，骨料的影响正如上面所分析的情况，如果骨料尺寸相对较大，就需要将含骨料混凝土看作是由骨料和砂浆组成的复合靶板进行分析。

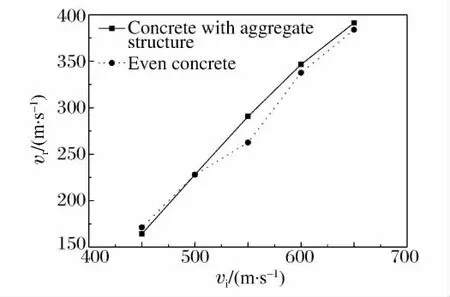
图3 含骨料混凝土的数值建模对剩余速度的影响Fig.3 The influence of aggregate structure on the residual velocity

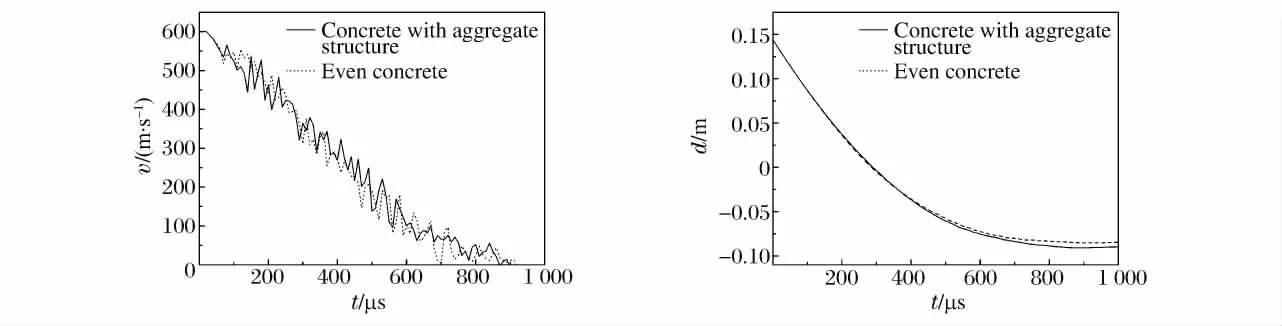
图4 含骨料混凝土数值建模对弹体速度和位移变化的影响Fig.4 The influence of aggregate structure on the velocity and displacement of projectile

4 结 论

采用二维拉格朗日弹塑性流体力学有限元程序LTZ－2D 探讨了含骨料混凝土的数值建模对混凝土侵彻及毁伤问题的影响，并分析了对含骨料混凝土的等效处理方法。在混凝土骨料尺寸相对弹体尺寸较小情况下，对于薄靶侵彻，低速撞击时骨料对弹体有阻碍作用，而速度较高时，由于靶板背面毁伤面积增大的原因，弹体的剩余速度增大；对于厚靶侵彻，相对于等效混凝土靶，含骨料混凝土的数值建模对弹体的侵彻过程影响不大。分析结果可以为混凝土侵彻问题的数值分析提供参考。

［1］ Vervuurt A，Schlangen E，Van Mier J G M.Tensile cracking in concrete and sandstone：Part 1－Basic instruments［J］.Materials and Structure，1996，26（1）：9－18.

［2］ 刘光廷，王宗敏.用随机骨料模型模拟混凝土材料的断裂［J］.清华大学学报：自然科学版，1996，36（1）：84－89.Liu Guang－ting，Wang Zong－min.Numerical simulation study of fracture of concrete materials using random aggregate model［J］.Journal of Tsinghua University：Science and Technology，1996，36（1）：84－89.

［3］ Thoma K，Riedel W，Hiermaier S.Mesomechanical modeling of concrete shock response experiments and linking to macromechanics by numerical analysis［C］∥ECCM Conference München，1999.

［4］ Hill R.Elastic properties of reinforced solids：Some theoretical principles［J］.Journal of the Mechanics and Physics of Solids，1963，11（5）：357－372.

［5］ 张凤国，李恩征.大应变、高应变率及高压强条件下混凝土的计算模型［J］.爆炸与冲击，2002，22（3）：198－202.Zhang Feng－guo，Li En－zheng.A computational model for concrete subjected to large strains，high strain rates，and high pressures［J］.Explosion and Shock Waves，2002，22（3）：198－202.

［6］ 张凤国，李恩征.混凝土撞击损伤模型参数的确定方法［J］.弹道学报，2001，13（4）：12－16.Zhang Feng－guo，Li En－zheng.A method to determine the parameters of the model for concret impact and damage［J］.Journal of Ballistics，2001，13（4）：12－16.

［7］ Holmquist T J，Johnson G R，Cook W H.A computational constitutive model for concrete subjected to large strains，high strain rates and high pressures［C］∥Proceeding of the 14th International Symposium on Ballistics.USA：American Defense Prepareness Association，1993：591－600.

［8］ 张凤国.动载荷作用下混凝土靶板损伤破坏的数值分析［J］.兵工学报，2009，30（9）：19－22.Zhang Feng－guo.Numerical analysis of the damage of concrete under dynamic loading［J］.Acta Armamentrii，2009，30（9）：19－22.