一种基于角谱理论的改进型相位恢复迭代算法*

刘宏展 纪越峰

1)(北京邮电大学，信息光子学与光通信国家重点实验室，北京 100876)

2)(华南师范大学，广东省微纳光子功能材料与器件重点实验室，广州 510006)

(2012年12月20日收到;2013年1月29日收到修改稿)

1 引言

相位恢复是指利用光的衍射理论，对输入光场进行衍射计算，得到输出面光场的场强分布，将其与实测(或理想)的输出场强数据进行比较，以能量转换效率最大、误差最小为准则，通过迭代或者搜索找到最符合实测(或理想)场强数据的相位分布.相位恢复是物理及工程中的一个基础性问题[1]，由于其在信号恢复、空间光通信、光学衍射元件的设计等场合有广泛的应用[2-4]，它已成为一个很重要的研究领域，其核心是要找到合适的相位恢复算法.而采用迭代算法进行相位恢复是当前主要的研究思路之一，并被运用到实践中[5].早在1972年，Gerehberg等[6]提出了G-S迭代算法，G-S算法简单而实用，但它的误差并不随着迭代次数增加而递减，相对于其他算法而言最小误差偏大，所得结果是相对最优.在此基础上，发展了许多改进算法，例如输入输出算法(IO)、混合输入输出算法(HIO)[7]等，可它们并不能保证迭代过程总收敛到正确解，有时甚至会停滞在某个局部极小值附近;另一方面，混合遗传-模拟退火算法[8]、免疫遗传算法[9]和蚁群算法[10]等也相继产生，但共同的缺点就是原理相对比较复杂，编程难度较大，且收敛速度相对较慢.以上算法都只适用于么正变换系统，基于此，杨国祯和顾本源提出任意线性变换系统中振幅-相位恢复的一般理论和杨-顾(Y-G)算法[11]，它已成功应用到各种实际问题和各种变换系统中.

本文结合星间卫星通信光学发射天线光束整形的实际需求，在传统G-S算法的基础上，提出了一种基于角谱传播理论的、能对复杂光场进行快速高精度相位恢复的幅度梯度加成迭代算法(下文简称加成算法)，即利用角谱传播理论，构建输入和输出面光场之间的正、逆向衍射过程，把整形要求达到的理想(或实际)输出光场振幅通过幅度参数加入到迭代过程的中间环节，并引入梯度方法，综合运用输入、输出光场信息，找到能量集中度高、误差小的相位分布.由于角谱理论严格满足亥姆霍兹方程，用它来处理迭代过程中输入、输出面光场间的衍射计算，可以得到更精确、可靠的结果[12];理想输出光强加入到迭代中间环节，使得迭代一次时便综合了输入、输出面的光强信息，不像传统的G-S那样只进行简单的替换，从而加速了迭代的速度;梯度法的引入，通过自适应的加大迭代步长，确保了对复杂光场相位恢复的良好收敛性.文章首先对算法中将要用到的角谱理论进行简短介绍，然后着重对新算法进行了描述与分析，最后对算法的性能，通过数值仿真进行了详细的比较.

2 算法描述与分析

要进行相位恢复迭代运算，就必须进行光场衍射及逆衍射运算，因此我们将首先简单介绍文中要用到的角谱理论，然后重点对加成算法进行描述与分析.

2.1 角谱理论

在直角坐标系中，令输入面平面坐标为xi，yi，输入光场振幅为U(xi,yi)、相位为φ(xi,yi);经某一空间距离d衍射后，在输出面的坐标为xo，yo，输出光场振幅为U(xo,yo)、相位为φ(xo,yo)，输入、输出光场的复振幅为Ei，Eo.引用傅里叶变换及逆变换符号：F{}，F-1{}，则由输入光场，获得输出光场的角谱衍射积分为[13]

H∗(fx,fy)是 H(fx,fy)的共轭，k=2π/λ，λ 为光波长，ΔLh为衍射光场的计算宽度，m，n均为采样点数，N为采样总数.由(1)，(2)式进行离散数值计算时，可借助快速傅里叶变换(FFT)完成.衍射光场的角谱理论严格满足亥姆霍兹方程，用它来处理相位恢复迭代算法过程中输入输出面光场间的衍射计算，可以得到更精确、可靠的结果，这为算法的设计提供了理论支撑.

2.2 幅度梯度加成迭代算法

传统G-S算法具有收敛速度较慢，对初始相位敏感等缺点，为了尽量消除这些不利因素，必须对传统G-S算法进行改进，本文把改进的算法称为幅度梯度加成迭代算法.其流程如图1所示.

其中W 为输出面整形光场的范围，βk，gk，γk的表达式是参考文献[14]得到的.

图1 幅度梯度加成迭代算法流程图

与传统G-S算法相比，文中提出的加成算法做了三方面的改进：一方面，通过变量参数α把实际(或理想)输出光场振幅与角谱衍射得到的输出光场振幅共同组成新的输出光场振幅，而不是像传统G-S算法那样，仅仅把角谱衍射得到的输出光场振幅用实际(或理想)输出光场振幅来替换.通过这样的处理，让每次的迭代衍射结果叠加在输出面光场信息中，并通过逆衍射过程，反馈回输入光场，从而构成了反馈环路，加速了迭代速度，具体见算法流程第4)步.另一方面，通过MATLAB中的自带angle()函数，直接对光场求对应的相位，避免了某些情况下，因出现分母取零奇点而迭代算法无法进行的情况，具体见算法流程第4)，6)步.第三方面，利用文献[14]的思想，把一种简单的梯度方法引用到迭代过程，在保证算法向目标最优解迭代的过程中，通过加大每次迭代的步长，加速了整个算法的收敛速度，且进行迭代时，不需要预先知道迭代值之外的其他信息，计算过程简单，具体见算法流程的第8)步.

3 加成算法仿真与结果分析

在星间激光通信系统中，因其通信距离达到几万公里，要求光束以近衍射极限发散角进行发射，加上有效星载的限制，光学天线多采用同轴两镜式反射望远镜结构[2].由于次镜对光束中心部分的遮挡，严重减损光束能量，因此，在光束进入发射天线前，必须对其进行有效的整形，使其变换成空心环状激光束，保证光束能量能够尽可能多地从光学天线发射出去.下边就以设计合适的星间激光通信星载光学天线光束衍射整形器为例子，来检验新提出的加成算法的功能.考虑到功率受限对星载系统的影响，光束整形应尽量保持光束的能量，因此具体迭代过程以能量集中度η为判断依据.

3.1 参数设置

具体参数如下，光波长λ=830 nm，整形后的高斯光束要求整形成外径R=3 mm，内径r=1.5 mm，即遮挡比为R/r=2的中空光束，从而减少光学天线中的次镜对光束能量的遮挡.高斯光束的束腰为0.75 mm，假设光束整形器放置在距入射光束束腰d=450 mm处，入射、出射光场所在平面的范围都设定为半径为5 mm的圆形区域，取样点数N=256.有了这些参数，利用(1)—(9)式，就上文中提出的加成算法，即可对其性能进行深入探讨.

3.2 仿真与分析

为了突出加成算法的优点，本节将从以下三方面着手：首先，从迭代速度以及误差下降速度与G-S算法进行比较;其次，通过初始相位取不同随机值，证明加成算法对初始相位是否具有适应性;最后，通过变换能量集中度η指标，证明算法是否具有收敛一致性.

先考查加成算法的迭代速度.从算法的流程图1可以看到，必须先确定幅度变量参数α，这里采用参考文献[15]中的试探法来实现，根据文中给出的数据，得到α=0.8.令输入光束的初始相位φ(xi,yi)=0，则新算法与G-S算法的相关数据如表1所示，表中列出了η分别为90%，94%时，两种算法的迭代次数与最小误差的取值.从表1可见，当η=90%，G-S算法的迭代次数为22次，加成算法为16次，加成算法的迭代速度略快，但随着能量集中度指标的提升，当η=94%时，GS算法要355次，而加成算法为213次，可见，加成算法的收敛速度明显优于G-S算法.另外，从最小误差来看，见表中第3、5列，似乎G-S算法能达到的最小误差的绝对值比加成算法小，但其实，它们都处在同一数量级上，因此从这个角度来看，它们能达到的最小误差是基本一致的.同样还是考察最小误差，若从单位迭代次数引起误差的下降速率来看，加成算法明显比G-S算法快.比如，利用表1数据，加成算法的误差下降速率=(0.1520-0.0950)/(213-16)=3.12×10-4，同理，G-S的下降速率=1.83×10-4，两者相比，得到加成算法单位迭代次数引起误差的下降速率是G-S的1.7倍.因此，在达到同样级别误差的约束条件下，加成算法收敛速度明显优于G-S算法.

表1 G-S算法与幅度梯度加成算法比较

由于G-S算法对输入光场的初始相位敏感，在进行迭代运算时，通常需要经过多次试探后，才能找到合适的初始相位值，进行迭代运算，这样费时费力.接下来，我们研究加成算法对初始相位的适应性.首先选定能量集中度η指标为90%，然后令输入初始相位φ(xi,yi为取值在[0 π]之间的随机数，具体由MATLAB中的rand()函数产生，进行一次完整的加成算法运算，得到当前随机初始相位下的迭代总次数M，并记录;重新产生新的随机初始相位φ(xi,yi)，进行新一轮加成算法运算，得到新的M值;依次重复10次，所得结果如2所示.

图2 不同随机初始相位下迭代次数的分布

图2中，横坐标表示初始相位取10次不同值时，对应的加成算法运行次序n，纵坐标表示加成算法运行一次的迭代总次数M.对于确定的能量集中度，从图2可以看到，当输入光场的初始相位随机变化时，加成算法的最小迭代次数为10次，最大为12次，绝大多数都是11次.因此，对于不同的随机初始相位值，加成算法表现出极好的适应性，它可以克服G-S算法对初始相位敏感的缺陷.不仅如此，与零初始相位相比，见表1中迭代次数的数据，初始相位取随机取值时，加成算法具有更快的收敛速度.

对于相位恢复迭代算法，都希望对于不同的随机初始相位值，算法最后都能收敛于最小的误差点.为此，令能量集中度η指标分别为90%，94%，分10次，对随机初始相位取不同的值，研究加成算法的收敛一致性，其仿真结果如图3所示.

图3 不同随机初始相位下迭代误差的分布

图3中，有两条图线，横坐标与图2的含义一致，纵坐标表示每次加成算法能达到的最小误差e.上边那条对应η=90%，10次运算的结果是，其迭代误差e密集分布在0.14两侧，即迭代误差趋向于0.14，可见，加成算法的迭代收敛具有一致性.同时，与初始相位为0时e=0.1520(见表1)相比，其误差有所减小.下边的图线对应η=94%，其迭代误差e更加密集地分布于0.09附近，与η=90%相比，此时迭代误差更加减小，且收敛一致性更优.这也从一个侧面说明，加成算法中用能量集中度η或者迭代误差e作为判断依据是统一的，这是因为，能量更集中了，自然迭代所能达到的最小误差便变小;而迭代误差变小了，则光束能量就更集中.

3.3 仿真实例

最后，设定能量集中度η以达到92%为标准，运用加成算法得到的星间激光通信光学天线光束整形器如图4所示.从图4(a)看到，迭代过程迭代误差e是单调递减的，能量集中度η是单调递增的，没有出现吉布斯现象[16]，而理想输出光场图4(b)与迭代所得光场图4(c)的误差e=0.1150.考虑到衍射光场边界的限制，在文中给定数据的约束下，当迭代误差进步一下降后，能量集中度η可以达到95%，因此，从能量利用率的角度来看，基于加成迭代算法进行光学天线光束整形器设计是可行的.图4(d)是所设计光束整形器的相位分布图，它决定了光束整形的最终效果，根据其分布，通过相关的运算、处理，运用衍射光学技术，就可以制作出来，其具体的器件实施过程，这里将不作讨论.

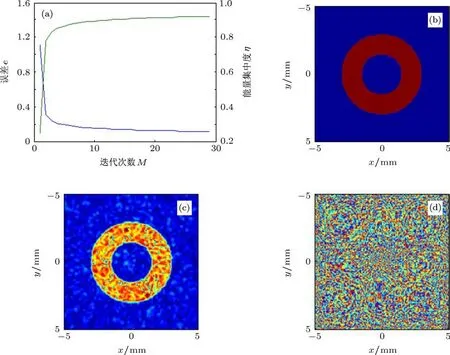
图4 仿真实例 (a)迭代误差、能量集中度与迭代次数关系图;(b)理想的整形光束幅度;(c)迭代所得整形幅度;(d)衍射整形元件的相位分布

4 结论

基于光场的角谱传播理论，在传统G-S相位恢复迭代算法的基础上，本文提出了一种幅度梯度加成相位恢复迭代算法.该算法通过引入幅度变量参数α，把输入光场的幅度信息通过正向衍射过程，加入到输出光场幅度的表征当中，并通过逆衍射过程，馈送至输入光场，形成反馈回路，从而加速迭代的收敛速度，而不像传统G-S算法那样只是单纯的把正向衍射得到的光场振幅用实际(或理想)的输出光场振幅置换，在整个迭代过程中，输入或输出光场的振幅都是单向传播，不能形成闭合回路，不利于加快迭代过程的收敛.另外，相对于传统的G-S，文中提出的加成算法在进行新一轮迭代过程时，引入了梯度运算，自适应地加大了迭代步长，从而也加快了收敛速度.从仿真结果看，在约束能量集中度η后，对于不同的随机初始相位，加成算法的最终迭代次数M趋同，可见，加成算法的收敛性并不依赖于初始相位分布，具有优良的适应性;与零初始相位相比，随机初始相位的迭代次数和最小误差都更小，这更加验证了加成算法对随机初始相位的适应性，而且收敛速度更快，这些都得益于幅度反馈与梯度的联合作用.不仅如此，对于设定的不同能量集中度标准，输入不同随机初始相位，新算法每次得到的最终迭代最小误差都趋于同一数值，比如，当η=94%时，最小误差e都密集分布在0.09附近，加成算法表现出优良的收敛一致性.综上所述，幅度梯度加成相位恢复迭代算法，具有收敛速度快，对初始相位适应性好，收敛一致性好等优点，它为复杂光场的相位恢复提供了一种新的方法，对设计衍射光学元件、光学整形器件，尤其是对能量集中度要求高的整形器件，提供了技术支持.

[1]Huang L X，YaoX，CaiD M，GuoY K，YaoJ，GaoF H 2010 Chin.J.Laser.37 1218(in Chinese)[黄利新，姚新，蔡冬梅，郭永康，姚军，高福华2010中国激光37 1218]

[2]Yu J J，Tan L Y，Ma J，Han Q Q，Yang Y Q，LiM 2009 Chin.J.Laser.36 581(in Chinese)[俞建杰，谭立英，马晶，韩琦琦，杨玉强，李密2009中国激光36 581]

[3]Wu R，Hua N，Zhang X B，CaoG W，ZhaoD F，Zhou S L 2012 Acta Phys.Sin.61 224202(in Chinese)[邬融，华能，张晓波，曹国威，赵东峰，周申蕾2012物理学报61 224202]

[4]Yu B，Peng X，Tian J D，Niu H B 2005 Acta Phys.Sin.54 2034(in Chinese)[于斌，彭翔，田劲东，牛憨笨2005物理学报54 2034

[5]Deng X P，ZhaoD M 2011 Appl.Opt.50 6019

[6]Gerchberg R W，Saxton W O 1972 Optik 35 237

[7]Fienup J R 1982 Appl.Opt.21 2758

[8]Lu Y，LiQ，Dong Y H，GaoH D，Ma Z G 2001 J.Opt.Laser 12 365(in Chinese)[鲁建业，李琦，董蕴华，高惠德，马祖光2001光电子激光12 365]

[9]Fang L，Ye Y T，Wu Y F，Lu J J，Yang X M，Cheng Z Q Opt 2006 Opt.El.Eng.33 42(in Chinese)[方亮，叶玉堂，吴云峰，陆佳佳，杨先明，成志强2006光电工程33 42]

[10]LiS L，LiH T，Yang X J 2008 J.Appl.Opt.29 758(in Chinese)[李社蕾，李海涛，杨喜娟2008应用光学29 758]

[11]Yang G Z，Gu B Y 1981 Acta Phys.Sin.30 410(in Chinese)[杨国桢，顾本源1981物理学报30 410]

[12]Goodman J W 1996 Introduction toFourier Optics(2nd EdN.)(New York：McGraw-Hill)p55

[13]LiJ C 2009 Acta Opt.Sin.29 1163(in Chinese)[李俊昌2009光学学报29 1163]

[14]Biggs D S C，Andrews M 1997 Appl.Opt.36 1766

[15]Wen C L，JiJ R，Dou W H，Song Y S 2010 Acta Opt.Sin.30 2473(in Chinese)[温昌礼，季家镕，窦文华，宋艳生2010光学学报30 2473]

[16]Deng X G，LiY P，Qiu Y，Fan D Y 1995 Chin.J.Laser B 4 447