X射线对金硅界面剂量增强效应的模拟研究

吴正新 何承发 陆 妩 郭 旗 艾尔肯阿不列木 于 新 张 磊 邓 伟 郑齐文

1（新疆大学物理科学与技术学院 乌鲁木齐 830046）2（中国科学院新疆理化技术研究所 乌鲁木齐 830011）3（新疆电子信息材料与器件重点实验室 乌鲁木齐 830011）

X射线对金硅界面剂量增强效应的模拟研究

吴正新1,2,3何承发2,3陆 妩2,3郭 旗2,3艾尔肯阿不列木1于 新2,3张 磊2,3邓 伟2,3郑齐文2,3

1（新疆大学物理科学与技术学院 乌鲁木齐 830046）
2（中国科学院新疆理化技术研究所 乌鲁木齐 830011）
3（新疆电子信息材料与器件重点实验室 乌鲁木齐 830011）

本文以光子与物质的相互作用机制为基础，论述了剂量增强效应的基本原理。用蒙特卡罗方法研究了金和硅交界时X射线入射产生的剂量梯度分布，通过MCNP5程序建立了一个三维的金硅界面结构模型，计算了不同厚度的金在金硅界面的剂量增强因子。计算结果表明：当X射线为30–300 keV时，界面附近硅一侧存在较大的剂量增强效应。金的厚度影响界面附近的剂量增强效果，当金的厚度为0–10 μm时，剂量增强因子随金的厚度增大；当金的厚度超过10 μm后，剂量增强因子随金厚度的增加而减少。

蒙特卡罗方法，剂量增强因子，界面，能量沉积，体元

随着半导体集成电路技术的飞速发展，为了改善器件性能，许多超大规模集成电路(VLSI)在芯片制造工艺中引入重金属工艺，为了提高器件可靠性，多数集成电路封装盖内层镀一层Au(如Kovar封装结构)[1]，高原子序数(如Au,W等)与器件灵敏区(主要成分为SiO2或Si)构成原子序数差异很大的界面，高原子序数材料对低能X射线有较大的光电吸收截面。因此，X射线在高原子序数材料中将产生大量的二次电子，部分次级电子进入交界面的半导体灵敏区中，在灵敏区产生明显的剂量增强效应[2–7]，从而使器件灵敏区沉积的能量超过了常规方法测量的平衡剂量值，器件损伤水平超过了预期，严重影响器件寿命和可靠性。通常以剂量增强因子DEF(Dose enhancement factor)表示剂量增强的程度，DEF定义为：DEF=界面区域剂量/平衡剂量。因而界面附近区域剂量深度分布的研究对半导体器件抗辐射加固及材料辐射效应的研究具有重要意义。

在半导体器件辐射效应研究中，吸收剂量的测量是在满足次级电子平衡等条件下，构造一个剂量计模体系统来测量标准介质或材料中的吸收剂量，然后换算至同样辐照条件的其他感兴趣材料的吸收剂量。由于换算过程涉及到带电粒子平衡厚度及该厚度对射线能谱的衰减修正等，实际操作比较繁琐。理论预测[8]指出，用该方法估计不同材料界面附近的实际剂量，将产生数倍的误差，此外，界面到均匀块介质之间的过渡区中能量沉积仅涉及窄小的几何尺度，实验测试比较困难。相比之下，蒙特卡罗程序[9]考虑的物理过程比较全面，计算中对光子和次级电子的所有次级过程都模拟跟踪，计算结果更接近真实值，产生的误差较小，因此，蒙特卡罗方法是研究剂量增强效应的有效途径。

本文通过三维蒙特卡罗光子-电子输运程序MCNP5，并根据辐射剂量学中的带电粒子平衡原理，提出了平衡剂量计算模型，模拟计算了不同能量的X射线在硅模体中心轴的剂量深度分布，对X射线及次级电子在金硅界面的传输进行了研究，模拟计算了不同能量的X射线在金和硅界面一侧的剂量与剂量增强因子随距离的变化关系及金厚度对界面剂量增强因子的变化情况。

1 MCNP程序及理论模型

1.1 MCNP程序及模拟粒子输运过程

MCNP程序(Monte Carlo N-particle transport code)是美国洛斯阿莫拉斯国家实验室开发的一种模拟粒子输运过程的蒙特卡罗程序, 是目前世界上公认较成熟的蒙特卡罗程序包之一[10]，可以用于计算复杂三维几何结构中的光子、中子、电子以及光子-中子-电子之间的耦合输运问题，也可以计算临界系统(包括次临界及超临界)的特征值问题，它适用于诸如反应堆和加速器的屏蔽计算、核环境污染及辐射剂量计算等核科学与技术方面的许多问题。

MCNP程序关于X射线在物质中输运主要考虑的物理过程为光电效应、康普顿效应、电子对效应，并分别产生光电子、康普顿电子以及正负电子对。电子在输运过程中会发生轫致辐射，模拟计算时先对源粒子抽样，抽取源粒子的空间位置、方向、能量、权重，确定初始状态(r, Ω, E, W)，然后用强迫碰撞抽样自由程距离l，新碰撞位置r’ = r + lΩ，在r’处确定粒子与某种物质的某种原子发生何类反应，由入射方向Ω、能量E和微分截面抽样出出射方向Ω’和出射能量E’，光子在输运过程中与核相互作用会产生电子，同样，电子在输运过程中会产生次级光子。对此，采取了先电子后光子的模拟原则。即当光子(包括源光子与次级光子)产生了次级电子时，先将原级光子存入光子库中，立即跟踪次级电子；当电子产生次级光子时，先将次级光子存入光子库，继续跟踪原级电子，对任一条分支都按此原则处理。当一个电子分支的历史结束后，首先清查电子库，若有库存电子时，便按后存入先取出的原则取出库内电子进行模拟。在确定电子库中已无电子后，再清点光子库，若有库存光子，同样进行。此时有可能产生电子，必须把光子存起来，跟踪电子。直到光子库无光子，再重新开始一个历史，直到全部粒子跟踪完毕。因此，对于X射线在金中产生的次级光子以及次级电子在界面的输运，MCNP5可以很好地进行模拟。

1.2理论模型

当X射线或γ射线照射到一种材料时，入射光子与物质原子发生的相互作用具有一定的几率，相互作用几率的大小可用截面来表示。X射线或低能γ射线与原子序数高的物质相互作用时，光电效应占优势。在非相对论情况下，即hv＜＜m0c2时，光子与原子K层束缚电子作用光电截面概率为：

其中，α=1/137为精细结构常数，m0c2为电子的静止质量，hv为光子能量，z为物质的原子序数，σth为汤姆逊散射截面。

在相对论情况下，即hv＞＞m0c2时：

在这两种情况下，都有σk正比于z5的关系，即随着z的增大，光电截面迅速增大。这是因为光电效应是X射线与γ光子和束缚电子的作用，z越大，则电子在原子中束缚得越紧，就越容易使原子核参与光电过程来满足能量和动量守恒要求，因而产生光电效应几率就越大。从式(1)和(2)还可以看到，σk随hv的增加而减少，低能时减小得更快一些，高能变化缓慢一些，X射线或者γ光子能量低时，电子被束缚得越紧，越容易发生光电效应，而当能量较高时，电子的束缚能相对来说可以忽略不计，这种电子接近“自由电子”，所以光电截面很小[11]。金原子序数是79，远远大于硅的原子序数14，因而当低能X射线通过金硅界面时，金中产生的光电子远多于硅中产生的光电子，这些光电子会通过界面非平衡扩散进入硅中，引起硅中的剂量增强。

本文用MCNP5程序建立一个三维的金硅界面结构模型，模拟计算的空间几何用笛卡尔坐标描述，分别在X、Y和Z坐标方向将受辐照材料划分成许多小格，划分的间隔在3个方向均不同，最后形成一个由许多小体元组成的矩形几何体(如图1所示)。

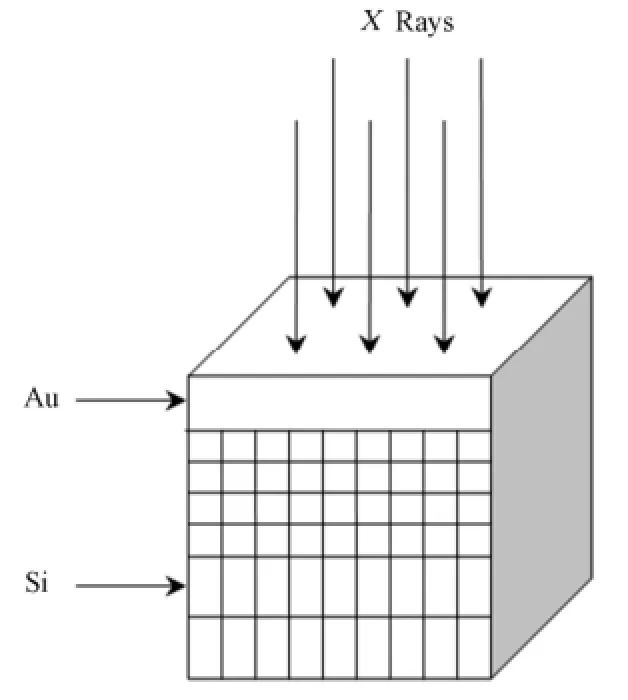
图1 计算几何条件示意图Fig.1 Sketch of geometric condition for calculation.

受辐照的金与硅尺寸分别为XYZ=9 cm× 9 cm×0.001/0.456 cm，(注:能量大于1 MeV时，因X射线的射程较长，须在整个模体底部加一厚度为1 cm硅的背散射层)，由于主要考虑硅模体表面区域的剂量分布，所以在划分硅材料时，深度方向单元尺寸为4层5 μm、4层10 μm以及45层100 μm，X和Y方向同为1 cm，从而整个硅模体被分割成4295个小体元。源模型简化为长20 cm、宽20 cm的正方形源，整个模体外部是空气，X射线垂直入射到金箔中，入射的粒子数为5×108，计算出各单元剂量值的不确定度小于2%。若设置的单元几何尺度过小，为达到较小的不确定度必须采用更大的入射粒子数，将耗费更多的机时。所用的计算机: Pentium Dual-Core CPU E6700，3.19 GHz，1.96 GB内存。模拟计算时采用光子与电子的联合输运方式，使用*f8卡记录各个小体元中的能量沉积即可得到各个点的剂量值，最后对正中心的体元进行取样，分析受X射线辐照后剂量随深度的分布参数。

因电子输运的计算量非常大，故模拟计算中使用MCNP5提供的能量截止卡，电子的截止能量选取为CUT: e=0.025 MeV，光子的截止能量选取为CUT: P=0.01 MeV。低于此能量的粒子被杀死，截掉了粒子径迹，因而能节省计算机时。表1中我们比较了能量截止值与缺省值的计算时间。从计算的结果可以明显看出，两种情况下吸收剂量值几乎吻合，不确定度也相对降低了一点，同时节约了68%左右的计算机时。

表1 计算机模拟时间比较(截止能量值与缺省值，对于0.1 MeV光子)Table1 CPU time comparison for energy cut-off values and default values in the simulation of 0.1 MeV photon.

2 模拟及讨论

为了计算平衡剂量，采用X射线辐照纯硅模体，其他条件不变的方法计算硅中的深度剂量分布曲线，得到平衡剂量。分别对0.03、0.05、0.07、0.1、 0.15、0.2、0.3、0.4、0.5、0.6、1.17、1.33 MeV各能点进行MCNP5计算10 h，最后对正中心的体元进行取样，即可分析X射线辐照后剂量随深度的分布参数。图2给出了不同能量的X射线在硅模体中心轴的剂量深度曲线。

图2 不同能量的X射线在硅模体中心轴的剂量深度曲线Fig.2 Central axis depth-dose curves in silicon phantom for X-rays at different energies.

从模拟结果可以看出，X射线在受照物质中的吸收剂量先随深度增长至一极大值，而后随深度逐渐递减。光子能量较低时，吸收剂量在物质浅层就达到最大值，主要是因为低能时光电效应的贡献远大于康普顿辐射的贡献。当光子能量较高时，次级光电效应减弱，对剂量的贡献逐渐低于次级康普顿效应[12]。考虑到次级电子的作用，靠近物质表面的浅层内，吸收剂量随深度增加。直到某一区域内电子的增加与因初始射线衰减而使电子释出的数目相等时，吸收剂量达到极大值，即为平衡剂量。从图中可以看出，对于能量为1.33 MeV与1.17 MeV的光子，最大剂量深度约为3 mm，即这两种能量光子在硅中的电子平衡厚度。此后，随物质层深度增加，材料对射线的衰减作用占优势，吸收剂量逐渐递减。

图3为不同能量的光子在金和硅界面一侧的剂量随距离的变化关系。

图3 金和硅界面的剂量随距离及能量的变化曲线Fig.3 Dose at Au/Si interface with variable distance for different energies.

从图3可以看出，入射能量不同的X射线在硅中的剂量分布也不同。能量低于0.3 MeV的X射线在界面附近存在明显的剂量梯度分布，这主要是因为X射线在物质中沉积能量可以分为两个步骤，即光子通过光电效应和康普顿效应将能量转移给产生的光电子、康普顿电子和俄歇电子，这些次级电子再将能量沉积于材料中，材料中的剂量分布主要与材料中产生的次级电子数量、能量射程、角分布等特性有关[13]，当0.03–0.3 MeV能量段的X射线入射在金硅界面时光电效应占主导作用，在界面附近产生的光电子和俄歇电子不平衡，导致了次级电子从金向硅中输运，将辐射能带到硅中，使界面附近沉积的能量不同于硅单独被光子辐照时的情况，因而在靠近界面附近区域(一般约为200 μm)以内产生极强的剂量增强效应。当能量超过0.4 MeV时，光子与物质的作用主要是康普顿效应，而康普顿效应对剂量增强效应贡献并不大，这是因为康普顿作用截面与材料原子序数关系不大，因而没有明显的剂量增强效应。图4给出不同能量的光子在金和硅界面一侧的剂量增强因子随距离及能量的变化关系。

图4 金和硅界面的剂量增强因子随距离及能量的变化曲线Fig.4 Dose enhancement factor at Au/Si interface with variable distance for different energies.

从计算结果可以看出，X射线能量不同，DEF也不同，存在一个峰值，在0.1 MeV时其剂量增强因子达到最大(19.98)，其原因是当光子的能量低于0.1 MeV时，虽然产生的光电子数目多，但是金对X射线的衰减也大。随着能量的增大，康普顿效应逐渐占优势，虽然金对能量大的X射线几乎没有衰减，但是在界面区域产生的净电子数目减少，因此，对应于某一光子能量存在一个极大值[14]。当能量大于0.4 MeV时，剂量增强并不明显，DEF接近1或者小于1。

为了研究高原子序数材料的厚度对界面剂量增强因子的影响，本文以金为例，硅模体的厚度仍为0.456 cm，其他条件不变，分别计算了金厚度为5、8、10、12、15、20、40、70 μm时界面的剂量增强因子。图5为典型X射线能量分别为100、150 keV剂量增强因子随金厚度的变化关系。从图中可以明显看出，金的厚度影响界面附近剂量效果，当金的厚度为0–10 μm时，剂量增强因子随金厚度增加；当金的厚度超过10 μm后，继续增加金的厚度，剂量增强因子随金厚度的增加而减少，符合射线与物质相互作用的指数衰减规律。而距离金硅界面越远，剂量增强系数越小，当金的厚度为10 μm时，距界面5、10、15、20、30 μm处的剂量增强因子分别为19.98、12.95、9.63、8.05、6.10。

图5 X射线为100 keV(a)、150 keV(b)时DEF和金厚度的关系Fig.5 Relationships between dose enhancement factor and the thickness of Au for an energy of X-ray of 100 keV(a) or 150 keV(b).■ 5 μm, ○ 8 μm, ▲ 10 μm, ☆ 15 μm, ◀ 20 μm

3 结语

利用蒙特卡罗方法研究了金与硅交界时X射线在界面硅一侧产生的剂量深度分布以及金的厚度对剂量增强因子的影响。计算结果表明：X射线在金硅材料界面及其附近的吸收剂量分布与单质硅材料中的平衡剂量相比有很大差异，对低能光子，这种现象尤其明显。当X射线为30–300 keV时，界面附近硅一侧存在较大的剂量增强效应，剂量增强因子最大值达到19.98。当光子能量超过1 MeV时，光子和物质的主要作用是康普顿效应，因而计算出剂量增强因子小于1，不产生剂量增强。当X射线能量相同时，由于射线平均自由程的限制以及高原子序数材料对射线的衰减作用，金的继续增厚不会使硅一侧剂量进一步增大。

该项研究工作为X射线引起的不同材料界面的剂量增强提供了理论手段，也可为半导体器件的抗辐射加固技术及材料辐射效应的研究提供有用的参考价值。此外，MCNP5作为一个大型蒙特卡罗粒子输运程序，其强大的几何处理能力和截面数据库可以解决很多实验中无法定量分析的问题，为实验提供依据。

致谢本工作得到东华理工大学核工程技术学院杨磊老师、西安交通大学核科学与技术学院王三丙博士和兰州大学核科学与技术学院谢芹同学的大力协作和支持, 在此一并表示衷心的感谢!

1 Chadsey W L. X-ray dose enhancement[Z]. VOL. I: Summary Report RADC-TR-76-159, ADAC26248

2 Wall J, Burke E A. Gamma dose distribution at and near the interface of different materials[J]. IEEE Transactions on Nuclear Science, 1970, 17(6): 305–309

3 Garth J C, Chadsey W L, Burke E, et al. Monte Carlo analysis of dose profiles near photon irradiated material interfaces[J]. IEEE Transactions on Nuclear Science, 1975, 22(6): 2562–2567

4 Garth J C, Burke E A, Woolf. The role of scattered radiation in the dosimetry of small device structures[J]. IEEE Transactions on Nuclear Science, 1980, 27(5): 1459–1565

5 Long D M, Millward, Wallace. Dose enhancement effects in semiconductor devices[J]. IEEE Transactions on Nuclear Science,1982, 29(5): 1980–1986

6 Kerric K G, Gorbics S G. Experimental determination of the low-enegry spectral component of Cobalt-60 sources[J]. IEEE Transactions on Nuclear Science, 1985, 32(8): 4356–4359

7 Long D M, Millward D G, Fitzwilson R L, et al. Handbook for dose enhancement effects in electronic devices[Z]. Rome air development center report, RADC-TR-83-84, 1983

8 Garth J C, Chadsey. X-ray produced charge depotion and dose in dielectrics near interfaces including space field and conductivity effects[J]. IEEE Transactions on Nuclear Science, 1974, 21(8): 235–242

9 许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京: 原子能出版社, 2006

XU Shuyan. Application monte carlo method in nuclear physics experiment[M]. Beijing: Atomic Energy Press, 2006

10 Judith F, Briesmeister. MCNP-5 general Monte Carlo N-particle transport code[R]. USA: Los Alamos National Laboratory, 2002

11 卢希庭. 主编. 原子核物理[M]. 北京: 原子能出版社, 2000: 63–68

LU Xiting. Nuclear physics[M]. Beijing: Atomic Energy Press, 2000: 63–68

12 何承发, 巴维真, 吾勤之. γ射线在界面附近金中的剂量分布[J]. 核技术, 1997, 20(3): 143–147

HE Chengfa, BA Weizhen, WU Qinzhi. Dose profiles of gamma rays in gold near interfaces with other materials[J]. Nuclear Techniques, 1997, 20(3): 143–147

13 Attix F H. Introduction to radiological physics and radiation dosimetry[M]. New York: John Wiley and Sons Press, 1986: 261

14 Garth J C. High energy extension of the semi-empirical model for energy deposition at interfaces[J]. IEEE Transactions on Nuclear Science,1981, 28(6): 4145–4152

CLCTL99

Monte Carlo simulation of dose enhancement effect of X-ray at Au/Si interface

WU Zhengxin1,2,3HE Chengfa2,3LU Wu2,3GUO Qi2,3ARKIN Abulim1YU Xin2,3ZHANG Lei2,3DENG Wei2,3ZHENG Qiwen2,3

1(School of Physics Science and Technology,Xinjiang University,Urumqi 830046,China)
2(Xinjiang Technical Institute of Physics and Chemistry,Chinese Academy of Sciences,Urumqi 830011,China)
3(Xinjiang Key Laboratory of Electronic Information Materials and Devices,Urumqi 830011,China)

Background:The dose enhancement factor of X-ray was found in 1970s, because of its bad damage to electronic devices. Purpose: This paper is mainly to calculate the dose-enhancement factor at Au/Si interfaces. Methods: The gradient distribution of dose with X-rays has been studied at and near the interface of Au/Si by Monte-Carlo simulation of particle transportation. The mechanism of dose enhancement is discussed based on the principles of interaction of photon with matter. A 3D Au/Si model has been established by MCNP5 program and the dose-enhancement factors of different thicknesses Au/Si interfaces were calculated by Monte Carlo method. Results: The calculated results demonstrate that there exists a stronger dose-enhancement in the Si side near the interface when the energy of X-ray is 30–300 keV. Conclusions: When the thickness of Au is 0–10 μm, dose-enhancement factor of X-ray increases along with the increase of the thickness of Au, when the thickness of Au exceeds 10 μm, dose-enhancement factor of X-ray decreases along with the increase of the thickness of Au.

Monte Carlo method, Dose-enhancement factor, Interface, Energy deposition, Voxel

TL99

10.11889/j.0253-3219.2013.hjs.36.060201

国家自然科学基金(10775178)资助

吴正新，男，1985年出生，2010年毕业于东华理工大学，现为新疆大学物理科学与技术学院硕士研究生，核技术及应用专业

何承发，E-mail: hecf@ms.xjb.ac.cn

2013-03-04，

2013-04-27