基于EMD的滚动轴承故障特征提取方法

夏均忠，苏涛，马宗坡，冷永刚，白云川

（1.军事交通学院汽车工程系，天津 300161；2.天津大学机械工程学院，天津 300072）

滚动轴承的故障诊断过程实质上是信号处理与模式识别的过程，前者的目的是从复杂、含噪的原始信号中提取表征故障本质的特征，而后者通过大量范例的学习，自主地对输入特征分类，进而识别具体故障。前者的输出结果需要作为后者的输入，因此如何从含噪振动信号中有效提取故障特征信号是轴承故障诊断的关键。

目前常用于滚动轴承故障特征提取的方法主要有：基于傅里叶变换的频域分析、高阶谱、时频分析、经验模式分解、随机共振理论[1]等。经验模式分解（Empirical Mode Decomposition，EMD）是基于信号的局部特征时间尺度对信号进行分解，分解出的各个分量突出了数据的局部特征，对其进行分析能更准确有效地把握原数据的特征信息。本文就该方法做了研究，并系统分析在此其基础上提出的希尔伯特-黄变换(Hilbert-Huang Transform，HHT)、局域均值分解(Local Mean Decomposition，LMD)以及集合经验模态分解(EnsembleEmpiricalMode Decomposition，EEMD)方法。

1 经验模式分解（EMD）

Huang N E等人[2]在对瞬时频率概念进行深入研究后创造性地提出本征模态函数（Intrinsic Mode Function，IMF）的概念及将任意信号分解为基本模式分量的新方法——EMD。这一创造性的方法提出后就迅速地被引入到故障诊断领域。

EMD把一个复杂的时间序列分解为有限个IMF之和，每一个IMF需满足以下两个条件：

（1）在整个时间序列内，极值点个数与过零点个数相同或相差最多不超过一个。

（2）由局部极大值点和局部极小值点分别形成的包络线的均值为零。

EMD分解的具体步骤如下[3]：

（1）假设信号为x(t)，取其上下包络局部均值组成的序列m(t)。

（2）令h1(t)=x(t)-m(t)，若h1(t)满足IMF条件，则其为第一个IMF分量；反之将h1(t)作为原始数据重复步骤（1）和（2）k次，得h1k(t)=h1(k-1)(t)-m1k(t)，使h1k(t)满足IMF条件获得第一个IMF，记做c1(t)=h1k(t)。

（3）从x(t)中减去c1(t)，得到残差

将r1(t)作为原始数据重复以上步骤，得到x(t)的第二个分量c2(t)。以此类推，当rn(t)为单调函数不能再提取IMF分量时，循环结束，得到n个IMF分量。最终信号x(t)被分解成n个IMF分量与一个余项的和

轴承发生故障时，在不同频带内的信号频率分布会发生改变，故可通过计算其振动信号某个IMF的频谱判断轴承是否发生故障。

文献[4]针对滚动轴承故障振动信号的调制特征和传统包络分析法的缺陷，提出基于经验模态分解和谱峭度的改进包络谱滚动轴承故障特征提取方法。文献[5]针对故障轴承振动信号中含有强烈的背景噪声，难以提取故障频率的现实情况，提出了基于经验模态分解和奇异值差分谱的轴承故障诊断方法。文献[6]应用基于EMD和自适应形态滤波的解调方法，进行滚动轴承故障信息的分离和故障特征频率提取。

EMD方法是一种自适应的局部化分析方法，EMD分解出的各个IMF分量突出了数据的局部特征，它从根本上摆脱了傅里叶变换的局限性，非常适用于非平稳、非线性过程。这种方法的主要缺点是对信号进行EMD时存在过包络、欠包络和边界效应、模态混淆现象。

2 希尔伯特—黄变换（HHT）

虽然EMD分解突出了数据的局部特征，但局部细节并不是很明显。由此Huang N E等人提出运用Hilbert变换对其进行包络分析。HHT首先对信号进行非线性的自适应分解——EMD，得到不同的本征模态函数（IMF），然后利用Hilbert变换研究信号的时频能量分布，提供更为清晰的局部细节时频特征[7]。

对信号x(t)进行EMD分解，分解后的信号用式（2）表示。

对其中的每一个IMF做Hilbert变换得

构造IMF解析函数

可得到幅值函数ai(t)及相位函数θi(t)，进一步得到瞬时频率ωi(t)。这样，信号x(t)就可以展开为以下形式

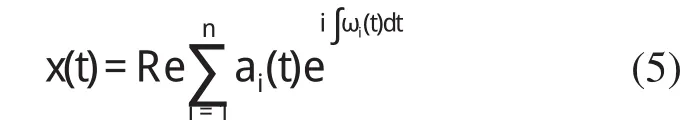
式中Re表示取实部。

最终得到信号的Hilbert谱及Hilbert边际谱，分别如下

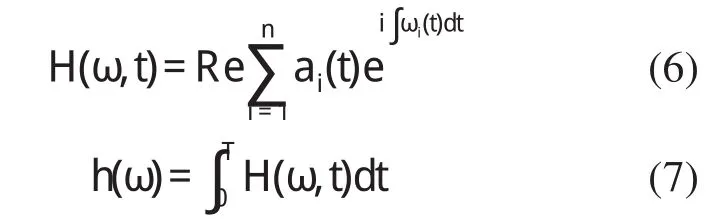
若Hilbert边际谱某个频率处有幅值，则表示原信号中这个频率的振动成分存在，因此可通过边际谱找到轴承故障频率，判断轴承故障发生位置。文献[8]分别运用EMD和HHT对滚动轴承提取不同瞬时频率和振幅的多组非平稳信号的故障特征，并对结果做了分析比较。文献[9]针对滚动轴承外环和内环发生故障时轴承产生的振动信号具有调制特点，提出基于Hilbert变换的滚动轴承内、外环故障诊断方法，运用Hilbert变换对其振动信号进行包络解调，实现载波和调制波的分离。

HHT方法的优点表现为它是一种自适应信号处理方法，适合于处理非平稳非线性信号。这种方法的主要缺点是对信号进行EMD时同样存在过包络、欠包络和端点效应现象；利用Hilbert变换形成解析信号后计算瞬时频率时会产生无法解释的负频率等问题；另外运用HHT时频谱图对故障分类时，仍需要人的主观判断，缺乏智能性，因此，把HHT时频谱图与智能算法相结合起来，进一步提高其智能性是未来的研究方向。

3 局域均值分解（LMD）

EMD分解存在明显的边界效应，且分解后的分量包含的频率和包络信息较少，另外Hilbert变换会产生负频率现象,针对以上问题就发展提出了LMD。

LMD是Smith于2005年提出的一种基于EMD的自适应非平稳信号的分析方法[10]。它可将任何一个复杂非平稳信号分解成多个瞬时频率且具有物理意义的生产函数（Product Function，PF）之和，其中每个PF分量都是由一个包络信号和一个纯调频信号相乘而得到的，包络信号是该PF分量的瞬时幅值，而PF分量的瞬时频率则可由纯调频信号直接求出；求出所有PF分量的瞬时频率和瞬时幅值后，再进一步组合，就可得到原始信号完整的时频分布。

对信号x(t)进行LMD的过程如下

（1）将局部均值函数m11(t)从原始信号x(t)中分离出来，得到

再用h11(t)除以局域包络函数a11(t)来对h11(t)进行解调，得

若s11(t)是纯调频信号，则它对应的局域包络函数a12(t)=1；若a12(t)≠1，则将s11(t)作为原始数据重复以上迭代过程，直至s1n(t)为一纯调频信号。因此有以下算法

（2）得到PF分量瞬时幅值函数，即PF分量的包络信号

（3）得到原始信号的第一个PF分量

（4）将PF1(t)从信号x(t)中分离出来，得到新信号μ1(t)，将μ1(t)作为原始数据重复以上步骤，循环k次，直到μk为单调函数为止。这样信号x(t)分解成k个PF分量与μk之和，即

式中μk是残余项，PFp(t)为包络信号和纯调频信号的乘积。即

将LMD引入到故障诊断中，通过分解和变换故障信号进行分析处理，经过分解可把信号分解成多个频率成分的组合，通过这些频率的对比，就可分辨出其故障特征。

文献[11]提出一种基于LMD包络谱和SVM（支持向量机）的滚动轴承故障诊断方法，对振动信号分解得到的PF分量进行包络分析并从包络谱中提取特征幅值比作为特征向量用于故障诊断。文献[12]对滚动轴承振动信号进行LMD分解后将具有明显冲击特征的PF分量进行FFT得到其频谱图，从图中可清晰地观测到故障频率。文献[13]应用LMD的能量算子解调方法提取故障特征信息，为提高分析精度，提出特征趋势正弦函数数据延拓方法以有效克服边界效应的影响。文献[14]结合LMD和Wigner高阶矩谱进行轴承故障诊断，实验结果验证了该方法的有效性。

LMD的主要优点为其生产函数PF与EMD的IMF相比可保存更多的频率和包络信息；其迭代次数少，运算速度快，边界效应不明显；基于LMD的时频分析结果比Hilbert谱在时频谱中能量更集中，且避免Hilbert变换在计算瞬时频率时产生的无法解释的负频率现象；它能根据信号本身特点进行自适应分解，分解后的每个PF分量都有一定的物理意义，能更好地反映实际系统的状态和信号内在本质。存在的主要问题是：平滑次数较多时，信号会发生提前或滞后现象，平滑时步长不能最优确定。

4 集合经验模态分解（EEMD）

EEMD是由Huang N E等人在EMD的基础上提出的一种新型信号处理方法[15]。

与前面几种方法相比它的应用范围更加广泛，诊断精度也要优于前面几种方法，且克服了EMD分解的模态混淆问题。

集合经验模式分解是把包含了信号和有限幅值白噪声的全体测试均值定义为真实IMF分量，其本质就是一种叠加高斯白噪声的多次EMD分解，利用高斯白噪声具有频率均匀分布的统计特性，使加入噪声后的信号在不同尺度上具有连续性[16]。尽管附加的噪声可能导致较小信噪比，但它可提供一个均一化的相关尺度分布以克服模态混淆，其中所谓的

式中r(t)为最终的残余分量，代表信号的平均趋势。本征模分量cj(t)(j=1,2,…)代表信号从高到低不同频段的成分，每个频段所包含的频率成分是不相同的，携带的能量也是不同的，并且二者会随着振动信号x(t)的变化而变化。

文献[19]提出EEMD与多尺度主元分析（MSPCA）相结合的方法进行轴承故障检测；该方法首先自适应地将信号分解到不同时间尺度，然后对其中的主要成分进行分析。文献[20]将轴承振动信号通过EEMD分解成若干IMF并以每个IMF的Renyi熵值为特征向量并结合主元分析来进行故障诊断。文献[21]针对旋转机械振动信号的非平稳、非线性等特点，提出基于EEMD的奇异熵谱故障诊断方法。

EEMD方法是一种自适应的信号处理方法，对平稳信号、非平稳信号、非线性信号都适用。通过多次对目标数据加入随机白噪声序列保证了不同区域信号映射的完整性，并且克服了传统EMD分解造成的模态混淆问题，从而提高了信号模态分解的准确性；另外通过该方法得到的IMF分量更能反映故障真实内涵，失真较小。此方法的缺点是它需要添加白噪声，可能会导致较小的信噪比；另外EEMD分解过程中的两个重要参数，即白噪声幅值和EEMD分解次数的选取是难点和关键，人为因素较大。模态混淆是指1个IMF分量包含很大的特征时间尺度或者相近的特征时间尺度分布在不同的IMF分量中[17]。

EEMD的分解步骤和原理如下[18]：

（1）在原始信号x(t)中多次加入幅值均值为0、标准差为常数的白噪声ni(t)，即

（3）重复以上两个步骤N次。将上述对应的IMF进行总体平均运算，消除多次加入高斯白噪声对真实IMF的影响，最终得到EEMD分解后的IMF为

5 结语

EMD是一种自适应的局部化分析方法，EMD分解出的各个IMF分量突出了数据的局部特征，从根本上摆脱了傅里叶变换的局限性。HHT使得EMD分解后的局部细节时频特征更加明显。LMD改善了EMD分解的边界效应，基于LMD的时频分析结果比Hilbert谱在时频谱中能量更集中，且避免Hilbert变换在计算瞬时频率时产生的无法解释的负频率现象；它能根据信号本身特点进行自适应分解，分解后的每个PF分量都有一定的物理意义，能更好地反映实际系统的状态和信号内在本质。EEMD通过多次对目标数据加入随机白噪声序列保证了不同区域信号映射的完整性，克服了EMD分解造成的模态混淆问题，提高了信号模态分解的准确性。

随着滚动轴承故障诊断技术的发展，单一的振动信号故障特征提取技术已不能很好地满足故障诊断要求,为提高诊断的效率和准确率，多种技术方法的结合运用成为其发展方向。EMD和能量算子、AR模型、奇异值分解、神经网络、时频熵、分形维数、近似熵、ICA、循环平稳、STFT[22]、等方法结合应用，是滚动轴承故障特征提取的研究方向。

[1]夏均忠，刘远宏，马宗坡，等.基于调制随机共振的微弱信号检测研究[J].振动与冲击，2012，31（3）：132-135.

[2]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London,1998,454(1971):903-995.

[3]Xiaomin Zhao,Tejas H.Patel,Ming J.Zuo.Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J].Mechanical Systems and Signal Processing,2012,27:712-728.

[4]蔡艳平，李艾华.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击，2011，30（2）：167-172.

[5]张超，陈建军.基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J].振动工程学报，2011，24（5）：539-545.

[6]周川，刘畅，伍星，等.基于EMD和自适应形态滤波的解调方法及其应用研究［J］.机械科学与技术，2011，30（8）：1376-1380.

[7]钟飞，张伟.Hilbert-Huang变换去除可控震源谐波畸变[J].清华大学学报（自然科学版），2011，51（6）：862-867.

[8]Michael Feldman.Theoretical analysis and comparison of theHilberttransform decomposition methods[J].Mechanical Systems and Signal Processing,2008,22:509-519.

[9]黄中华，谢雅.基于Hilbert变换的滚动轴承内环和外环故障诊断［J］.中南大学学报，2011，42（7）：1992-1996.

[10]Smith J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface,2005,2(5):443-454.

[11]李志农，刘卫兵.基于局域均值分解包络谱和SVM的滚动轴承故障诊断方法研究[J].机械设计与制造，2011，11（11）：170-172.

[12]于雯，陈晓平.局域均值分解法在轴承故障诊断中的应用[J].轴承，2011，(9)：49-52.

[13]鞠萍华，秦树人，赵玲.基于LMD的能量算子解调方法及其在故障特征信号提取中的应用［J］.振动与冲击，2011，30（2）：1-4.

[14]刘卫兵，李志农，蒋静.基于局域均值分解和Wigner高阶矩谱的机械故障诊断方法的研究［J］.振动与冲击，2010，29（6）：170-173.

[15]Wu Z H,Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances inAdaptive DataAnalysis,2009,1(1):1-41.

[16]张玲玲，廖红云.基于EEMD和模糊C均值聚类算法诊断发动机曲轴轴承故障[J].内燃机学报，2011，29（4）：332-336.

[17]张玲玲，骆诗定，肖云魁，等.集合经验模式分解在柴油机机械故障诊断中的应用[J].科学技术与工程，2010，10（27）：6745-6749.

[18]陈略，訾艳阳，何正嘉，等.总体平均经验模式分解与1.5维谱方法的研究［J］.西安交通大学学报，2009，43（5）：94-98.

[19]Matej Žvokelj,Samo Zupan,Ivan Prebil.Multivariate and multiscale monitoring of large-size low-speed bearings using ensemble empirical mode decomposition method combined with principalcomponentanalysis[J].Mechanical Systems and Signal Processing,2010,(24):1049-1067.

[20]窦东阳，李丽娟.基于EEMD-Renyi熵和PCA-PNN的滚动轴承故障诊断[J].东南大学学报，2011，（41）：107-111.

[21]高清清，贾民平.基于EEMD的奇异谱熵在旋转机械故障诊断中的应用［J］.东南大学学报，2011，41（5）：998-1001.

[22] Robert B.Randall,Jerome Antoni.Rolling element bearing diagnostics-A tutorial[J].Mechanical Systems and Signal Processing,2011,25:485-520.