适用于任意接收机航迹的无源WiMAX－SAR成像方法

汪 玲 庄旭昇 庞 铄

（南京航空航天大学电子信息工程学院，南京，210016）

引 言

随着电子对抗技术的发展，传统有源雷达面临着电子干扰、超低空突防、反辐射导弹和隐身技术的严重威胁。在这种形势下，收发分置的无源雷达体制引起了雷达界的广泛关注。无源雷达由于自身不发射信号，因此具有较强的抗电子干扰、抗反辐射导弹、抗低空突防和反隐身的能力，并且具有成本低、可靠性高、生存能力强的优点［1，2］。

基于外部辐射源（也称为机会照射源）的无源合成孔径雷达（Synthetic aperture radar，SAR）是无源雷达的研究重点之一。目前可利用的机会照射源包括调幅（Amplitude modulation，AM）和调频（Frequency modulation，FM）广播信号、电视信号、无线通信信号、全球定位系统（Global positioning system，GPS）信号等。WiMAX［3，4］（Worldwide interoperability for microwave Access），即全球微波互联接入，是一项新兴的基于IEEE 802.16标准的宽带无线城域网技术，使用2～66GHz频段，数据传输距离最远为50km，信号带宽可达20 MHz，若作为雷达照射源可提供的最大距离分辨率为7.5m，因此将WiMAX信号作为机会照射源进行SAR成像具有距离分辨率高和探测距离远的优势。

文献［5］研究了 WiMAX信号的双基模糊函数，从理论上说明WiMAX信号应用于双基雷达系统的可行性。文献［6］对移动 WiMAX信号进行了波形分析和模糊函数分析，结果表明WiMAX信号作为雷达照射源有较大的实用价值。然而文献［5，6］仅仅是从模糊函数的角度对 WiMAX信号进行了理论分析，并没有将 WiMAX信号应用到真正的雷达系统中。文献［7］通过利用固定WiMAX信号进行了室内运动目标的被动雷达检测实验，但只得到了目标的轨迹信息，并未实现目标成像。文献［8］中研究了利用 WiMAX信号进行SAR成像的方法，但该方法仅适用于小转角情形。在文献［9］中提出了一种基于斜侧视圆周扫描的近场转台成像系统大转角成像算法。

本文在对已有文献的研究基础上，给出一种基于滤波反投影（Filtered back projection，FBP）原理的成像方法用于以WiMAX信号为照射源的无源SAR成像。该 WiMAX－SAR成像方法能够实现任意接收机飞行轨迹下的无源SAR成像。

1 信号模型

1.1 WiMAX信号

WiMAX是IEEE802.16系列标准的统称，也被称为802.16Wireless MAN（Wireless metropolitan area network）或802.16，其信号形式主要采用正交频分复用（Orthogonal frequency division multipex，OFDM）调制技术。OFDM是一种多载波数字调制技术，其子载波类型有以下三种：用于传送数据的数据子载波，用于信道环境估计的导频子载波和不发送任何数据的空子载波。

WiMAX信号的表达式为［10］

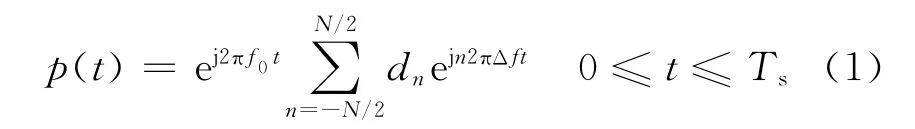
式中：Ts表示一个符号的持续时间；f0为载波频率；dn为第n个子载波上传输的复信号；Δf为每个子载波上的步进频率，即

1.2 WiMAX－SAR回波信号模型

在无源SAR系统中，设发射机发射波形为WiMAX信号，如式（1）所示。T，γR（s）分别表示发射机和接收机的飞行轨迹，通过Born近似可得接收的回波信号如下［11－13］

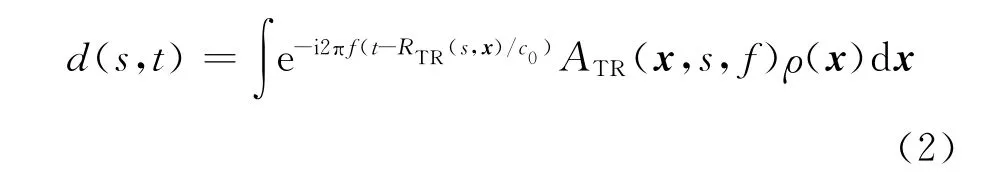
式中：s为慢时间；t为快时间；c0为光速；f为频率；x＝（x1，x2）表示地面目标二维坐标；x＝（x1，x2，ψ（x1，x2））表示目标的三维坐标，ψ是一个已知的平滑函数，称为地形因子；ρ（x）为场景反射率函数；RTR（s，x）＝｜T－x｜＋｜x－γR（s）｜表示发射机到目标和目标到接收机的总距离，称为双基距离；ATR（x，s，f）是一个与发射天线波束方向性图Jtr（x，T）、接收天线波束方向性图Jrc（x，T）、发射波形PWiMAX（f）（pWiMAX（t）的傅里叶变换）、几何延展因子等因素有关的复幅度函数，可以表示为

2 基于FBP的双基WiMAX－SAR成像方法

2.1 FBP原理

通过对回波信号d（s，t）进行逆运算处理，可得重建的场景反射率

式中｜f｜称为斜滤波器［15］，由其形式可知，该滤波器在时域的引入微分效果，因此可以增强重建图像边缘的锐化度；Q′TR称为匹配滤波器；则是用于补偿幅度调制影响和变量代换产生的额外项。

将式（14）代入式（13），可得

可见数据采集空间Ωz的大小决定了像素点z处的重建质量，类似于成像系统的“带宽”，带宽越宽，重建图像（z）越逼近真实图像ρ（x）。由式（15）可知，数据采集空间Ωz包含的向量方向取决于双基雷达的观察方向，这与发射机位置和接收机的飞行轨迹有关，向量长度与发射波形带宽，发射机和接收机相对地面点z的几何关系有关。

2.2 算法流程

根据2.1节的分析可知，经FBP处理得到的场景图像为

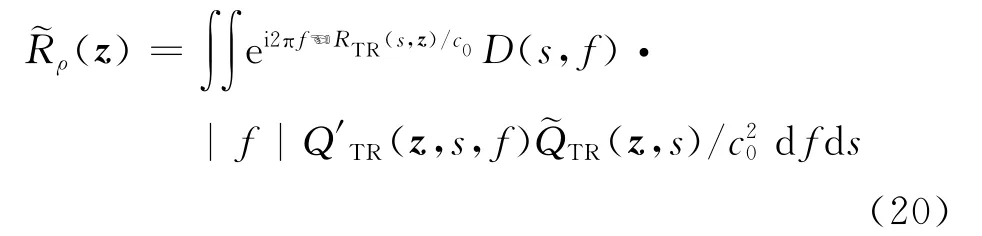
由此可给出FBP算法的处理步骤，同时给出每一步的算法复杂度（假设s，t的采样个数均为N，重建图像像素个数为N×N）。

（1）对接收信号d（s，t）在快时间上作傅里叶变换，即D（s，f）＝Ft［d（s，t）］，运 算 复 杂 度O（N2logN）；

（2）斜滤波和匹配滤波处理，得到滤波信号，即（s，f）＝D（s，f）｜f｜Q′TR（f），运算复杂度O（N2）；

（3）将滤波后信息向等距离线作反投影，即（z）运 算 复 杂 度O（N2logN）；

滤波处理和反投影处理是本算法的核心部分，是成像的关键，而运算可以采用快速BP算法［16］或并行处理，包括使用GPU进一步提高运算效率［17］。具体算法流程如图1所示。

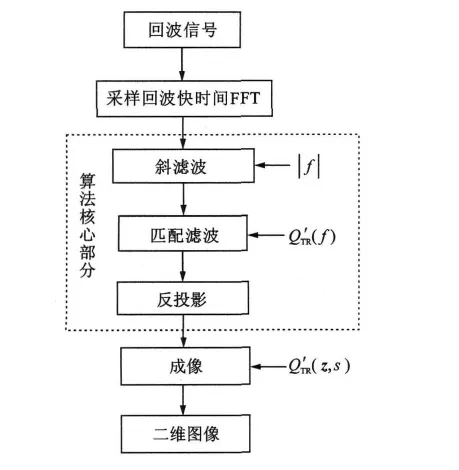
图1 FBP算法流程图

3 成像仿真验证

WiMAX信号参数设置为子载波数256，信号带宽20MHz，载波频率10GHz，循环前缀长度1.428 6μs，有效符号长度11.429μs，符号总长度12.185 7μs。场景大小设为22km×22km，划分成128×128个像素，其中像素点［1，1］和像素点［128，128］分别对应场景中的［0，0，0］km 和［22，22，0］km。假设场景中包含9个点目标，像素位置分别为（90，65）（40，65）（65，40）（65，90）（65，65）（90，40）（40，40）（90，90）（40，90），如图2所示。

根据接收机载机的飞行轨迹不同，设计两个实验，发射机位置和接收机飞行轨迹分别如图3和图4所示。接收信号采样频率fs为200MHz，孔径采样点数Na为2048，载机飞行速度v为261m／s。在两实验中，WiMAX 发射机位置为［0，0，6.5］km，接收机飞行轨迹分别为圆轨迹和直线轨迹，即γR，1（s）＝［11＋11cos（s），11＋11sin（s），6.5］km和γR，2（s）＝［0，10s／π，6.5］km，其中s∈［0，2π］。圆轨迹飞行时，成像孔径为全孔径，即一个圆周，接收机直线轨迹飞行时，成像所用孔径长度为20 km。

图2 仿真场景

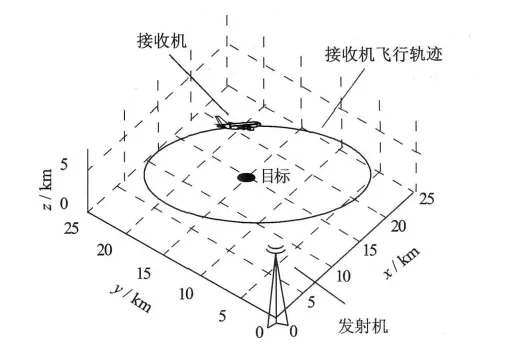
图3 实验1场景示意图（接收机圆轨迹飞行）

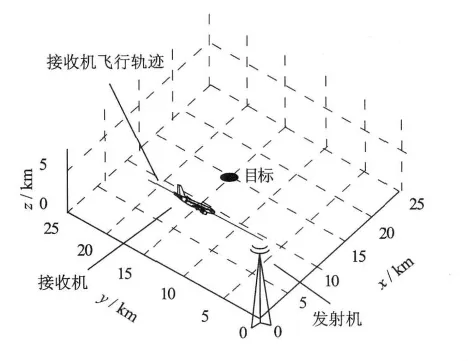
图4 实验2场景示意图（接收机直线飞行）

以WiMAX信号作为机会照射源，利用第2节中给出的FBP成像方法分别进行仿真实验1和仿真实验2，成像结果如图5和图6所示，其中图5（a）和图6（a）分别为两次实验的多点目标成像结果，图5（b）和图6（b）分别为两次实验中间位置点目标X方向剖面图，图5（c）和图6（c）为Y方向剖面图。成像结果表明该FBP算法在不同载机轨迹下均可实现WiMAX信号的无源SAR成像。由图5（b）和（c）分析可得，接收机圆轨迹飞行时，场景中间位置点目标X方向和Y方向的3dB宽度分别为16.79m和15.88m；由图6（b）和（c）分析可得接收机直线飞行时，场景中间位置点目标X方向和Y方向的3dB宽度分别为19.30m和31.93m。由此可知，实验1的成像效果较之实验2的成像结果要好。这是因为当接收机圆轨道飞行时，数据采集空间Ωz包含了所有观察方向，图像各部分边缘能够较好重建；而当接收机直线飞行时，Ωz仅包含部分观察方向，因此只有某些方向的边缘被重建。

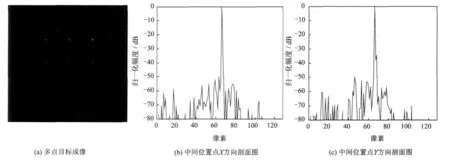
图5 无源SAR，接收机圆轨迹飞行时成像结果

图6 无源SAR，接收机直线飞行时成像结果

4 结束语

本文给出了一种采用WiMAX信号进行无源雷达成像的方法，通过对场景 WiMAX回波信号进行FBP处理，得到场景反射率。该方法适合于任意接收机轨迹情况下的无源 WiMAX－SAR成像。文中给出了接收机载机不同飞行轨迹下的多点目标成像结果，验证了所研究的 WiMAX－SAR成像方法的有效性。在本文中假设接收机的航迹信息已知，若存在误差，可以采用自聚焦技术进行运动误差补偿。关于运动误差对图像重建质量影响的分析以及相应进一步的补偿方法将是下一步研究的内容。

［1］ 汤子跃，张守融.双站合成孔径雷达系统原理［M］.北京：科学出版社，2003.Tang Ziyue，Zhang Shourou.Bistatic synthetic aperture radar systems theory［M］.Beijing：Science Press，2003.

［2］ 王放，黎湘.双／多基地合成孔径雷达研究进展［J］.电光与控制，2010，17（4）：45－49.Wang Fang，Lin Xiang.Dual／multi－base synthetic ap－erture radar research［J］.Optics ＆ Control，2010，17（4）：45－49.

［3］ 郎为民，刘波.WiMAX技术原理与应用［M］.北京：机械工业出版社，2008：81－116.Lang Weiming，Liu Bo.Principles and applications of WiMAX technology［M］.Beijing：Machinery Industry Press，2008：81－116.

［4］ 彭木根，王文博.下 一 代 宽 带 无 线 通 信 系 统OFDM＆WiMAX［M］.北京：机械工业出版社，2007：174－231.Peng Mugen，Wang Wenbo.Next－generation broadband wireless communication system OFDM ＆WiMAX［M］.Beijing：Machinery Industry Press，2007：174－231.

［5］ Arroyo J，Jackson J，Temple M.WiMAX ambiguity function for PCL systems ［C］／／Proceedings of the IEEE 2010National Aerospace and Electronics Conference.Fairborn：IEEE，2010：54－59.

［6］ 汪清，候春萍，Lu Yilong.基于移动 WiMAX的被动雷达信号分析及模糊函数性质研究［J］.计算机应用研究，2010，27（6）：2226－2231.Wang Qing，Hou Chunping，Lu Yilong.The mobile WiMAX－based passive radar signal analysis and characterization of the ambiguity function［J］.Application Research of Computers，2010，27（6）：2226－2231.

［7］ 汪清，候春萍，Lu Yilong.基于固定 WiMAX的被动雷达系统研究［J］.传感器与微系统，2010，29（10）：55－58.Wang Qing，Hou Chunping，Lu Yilong.Fixed WiMAX based passive radar system research［J］.Sensors and Microsystems，2010，29（10）：55－58.

［8］ 庞铄，汪玲.采用WiMAX信号的无源SAR成像方法［J］.雷达科学与技术，2012，10（6）：607－612.Pang Shuo，Wang Ling.WiMAX signals using passive SAR imaging methods［J］.Radar Science and Technology，2012，10（6）：607－612.

［9］ 闫伟，杜卫民，许家栋，等.基于斜侧视圆周扫描的近场微波成像算法［J］.数据采集与处理，2013，28（1）：7－11.Yan Wei，Du Weimin，Xu Jiadong，et al.A near－field microwave imaging method based on side－looking circular scanning［J］.Data Acquisition and Processing，2013，28（1）：7－11.

［10］Committee L S.IEEE standard for local and metropolitan area networks.part 16：Air interface for fixed broadband wireless access systems［S］.New York，USA：IEEE Std，2009.

［11］Nolan C J，Cheney M.Synthetic aperture inversion［J］.Inverse Problems，2002，18（1）：221－236.

［12］Nolan C J，Cheney M.Synthetic aperture inversion for arbitrary flight paths and non－flat topography［J］.IEEE Trans Image Process，2003，12（9）：1035－1043.

［13］Cheney M.Synthetic－aperture assessment of a dispersive surface［J］.International Journal of Imaging Systems and Technology，2004，14（1）：28－34.

［14］Yarman C E，Yazici B.Synthetic aperture hitchhiker imaging［J］.IEEE Transactions on Image Processing，2008，17（11）：2156－2173.

［15］Natterer F，Wubbeling F.Mathematical methods in image reconstruction［M］.Philadelphia，PA：SIAM，2001.

［16］Nilsson S.Application of fast backprojection techniques for some inverse problems of integral geometry［D］.Linkoping，Sweden：Linkoping University，1997.

［17］Capozzoli A，Curcio C，Liseno A.GPU－basedω－k tomographic processing by 1dnon－uniform FFTs［J］.Progress in Electromagnetics Research M （PIERM），2012，23：279－298.