一种高效率的RPIM法及其在电磁场中的应用

王立鹏，王欣彦，战洪仁，张先珍，寇丽萍

(沈阳化工大学，辽宁沈阳110142)

0 引 言

近些年来发展的无单元法不需要生成网格，通过节点来构造插值函数，在国内外受到高度重视，成为热门的数值计算方法。无单元法在分析裂纹扩展、特大变形、碰撞、金属冲压成型等很多问题具有优势［1］。无单元法也可被用来解决电磁场数值计算网格限制的问题［2-7］。目前，已有多种无单元法，径向基点插值型无单元法［8］是其中一种。径向基函数(RBF，Radial Basis Fuction)是以点x到节点xi之间的距离为自变量构成的一类函数，也叫距离基函数。它具有求解效率高、运算简单、各向同性和空间维数无关等优点，几乎可以逼近所有的函数。因此，在多元逼近论中用径向基函数进行插值已成为一种有效的工具。常用的径向基函数有数种，其中的复合2次Multiquadrics(MQ)径向基函数由于具有较高的收敛率［9］，应用较为广泛。

然而，无单元法的计算量较大，其求解效率不及有限元法。通常，无单元法的求解采用迭代方法，包括高斯-赛德尔(Gauss-Seidel)迭代、松弛迭代、共轭梯度法(Conjugate Gradient，CG)、广义最小余数法等。

目前，在迭代求解方法中，多重网格法是一种比较热门的求解方法。简单地说，多重网格法是采用不同尺度的网格，先在细网格上进行光滑迭代，消除高频误差，然后通过限制算子R将细网格上残差转换至粗网格，再通过粗网格来消除低频误差，这样一层一层传下去，然后残差又通过延拓算子R一层一层返回到细网格上，对先前的细网格迭代解进行修正。这就是应用较为广泛的V循环多重网格法的思想。

上世纪60年代，多重网格方法(MG)开始出现，起初并未受到重视。从20世纪70年代开始，多重网格法成为研究热点，得到了快速的发展，现在已成为一种有效的数值方法，用来求解偏微分方程组离散化形成的大型代数方程组［10-18］。多重网格法的主要优点是它具有快速收敛性，收敛速度与网格尺寸无关。该方法可应用到电磁场的数值分析中［19］。

多重网格法是以有限差分法为架构来引入多重网格的校正与迭代技术，实质上是多重网格有限差分法。因而，同有限差分法一样，多重网格法对复杂的定解条件、复杂的边界几何结构等方面问题模拟较为困难。

多重网格法求解技术同有限单元法相结合［20］，可提高求解效率，正被用来求解各种数值计算问题。目前，该方法在无单元法的应用还很有限，多重网格法已被用在无单元伽辽金法上来求解电磁场问题［21］，但这种高效的求解方法还未被应用到径向基点插值型无单元法。本文将径向基点插值型无单元法同多重网格法思想相结合，提出基于径向基点插值型无单元的多重节点法，该方法在粗节点的构造方法及限制算子的确定等方面都与有限元多重网格法有所区别。通过算例分析，证明多重节点法可获得较为理想的径向基点插值型无单元法的求解效率。

1 径向基点插值型无单元多重节点法(RPIM－MN)原理

1.1 多重节点法(MN)

多重网格法是基于网格基础之上的，在有限单元法、有限差分法等以网格为基础的离散方法中都有广泛的应用。而无单元法本身指的是通过一组散布节点来构造场函数的近似表达式，可以消除网格，即使有背景网格也只是用来进行积分计算的。可见，以网格为基础的多重网格法并不是为无单元法量身定做的。但是，可以借鉴高效求解的多重网格法的思想，将其引入到无单元法的求解中，这就是多重节点法。

为了简单起见，只分析用粗细两层无单元节点。在细节点的离散场域上，实施径向基点插值型无单元法求解给定的线性方程组:

式中:KH为粗节点线性系统的系数矩阵;ΩH为粗节点求解域;rH为残差。

该方法的计算步骤如下:

(1)前光滑迭代计算，对KHxH=bH进行细节点迭代，得到近似的解υH，并计算细节点近似解的残差。

(2)对残差进行限制，rH←R(bυh-Khυh，由 Ωh向ΩH转移。

(3)在ΩH上解残差方程。设υH=0，解KHxH=rH，用υH作为近似的解。

粗节点系数矩阵:KH=RKhP

(4)插值，由向ΩH向Ωh转移校正量，并修正Ωh上的解:

由R=σPT可确定P，其中σ为比例系数。

(5)后光滑迭代计算，ε0为一个任意小的正数，若 ε≥ε0，转向步骤(1)。

1.2 径向基点插值型无单元多重节点法(RPIMMN)

在粗节点的构造方法及限制算子的确定方法上，径向基点插值型无单元多重节点法同有限元多重网格法有所区别。

(1)粗节点的构造算法

该法采用了聚集式的方法构造粗节点，也就是从初始细节点中，按一定地方式选出粗节点，不再另外布置新点。具体如下:

(a)为每个节点k确定一个“影响值”v(k)，其值等于节点k的影响域内节点数目。

(b)对于边界节点，首先将边界几何结构突变点选作粗节点;然后按“影响值”从大到小选取N个节点为粗节点。N约为边界节点总数的一半。

(c)对于内部节点，按“影响值”从大到小选取M个节点为粗节点。M约为节点总数的一半。

(d)对于均匀布点，可在细节点的基础上间隔的选取粗节点。

(e)将新粗节点的影响域中所有未定点变为细节点。

图1表示了均匀布点情况下，两重节点法的粗、细节点布置及各节点的支撑域。图中的圆形区域为各节点的影响域。

图1 径向基点插值型无单元多重节点法示意图

(2)限制算子R的确定

对无单元法来说，限制算子R是指将细节点上残差限制到粗节点上的映射矩阵。限制算子是根据粗、细节点的位置来确定的。由于没有网格的束缚，径向基点插值型无单元两重节点法粗节点和细节点之间的映射关系较为简单，可采用节点间的距离函数来构造。本文讨论两重节点(细节点层为k，粗节点层为k-1)的迭代情况。

限制算子矩阵元素:

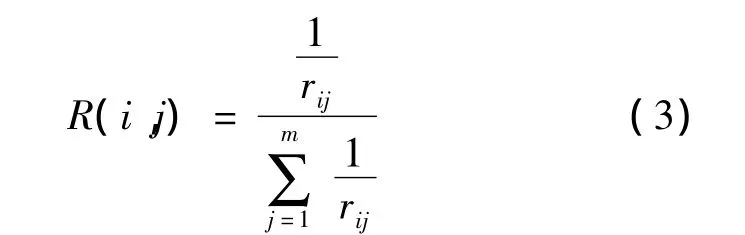
式中:i为任意一个粗节点号;j为任意一个在粗节点i影响域内的无单元节点号(不包括i节点);m是粗节点i影响域内节点数;rij表示粗节点i与节点的距离。

按式(3)，限制算子R可以根据细节点和粗节点在场域中的相应位置来确定。

延拓算子P可根据P=RT来确定。

上述算法也可以类推，形成径向基点插值型无单元多重节点法。

2 计算实例

算例一:一长直接地金属槽，a=0.1 m，槽内电位函数 φ(x，y)满足 Laplace方程，φ0=10 V，边界条件如图2所示。取第一类边界上罚因子为10 000;在计算中采用了二重节点，51×51个细节点，26×26个粗节点，计算后再增加节点数，比较多重节点法(MN)与共轭梯度法(ICCG)的计算结果，如图3所示。可以看出，同 ICCG法相比，MN法的计算时间要少得多。

算例二:一台长为55 mm、外径为53 mm的永磁直流电动机，该电机为瓦片形磁极结构，4对极8槽，钕铁硼永磁体磁化方向为平行磁化。其磁钢矫顽力为7.81×105A/m，所建立的场域模型如图4所示。

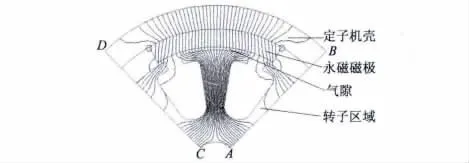
图4 永磁直流电动机空载磁场

对电机的空载电磁场进行分析，取一个极距为求解区域，AB边、CD边满足第二类齐次边界条件:

用无单元法离散电机电磁场域，分别采用MN法和ICCG法对其进行求解。MN法采用二重节点法，无单元细节点数为59 731，无单元粗节点数为29460。

通过计算，得到10-4精度要求下的电机磁力线分布，如图4所示。其中，二重节点法计算时间为187 s，ICCG法计算时间为294 s。

由于多重节点法的迭代计算是分散在各层中进行的，且粗节点数目较少，所以计算迭代次数时，粗节点的迭代次数必须折合到细节点，方便与单层ICCG法的迭代次数进行对比。

将W定义为总迭代数，其表达式:

式中:M为多重节点的层数;Nk为在第k层中的迭代次数。

由于在多层节点中，W相当于把各层的迭代计算次数都折算到最细层，然后叠加。由于忽略了限制算子和延拓算子的工作量，总迭代数可方便、粗略地估计多重节点法计算量。

比较多重节点法总迭代数与ICCG法的总迭代数，得到总迭代数与收敛容差之间的关系曲线，如图5所示。容易看出，在满足相同的精度条件下，多重节点法的总迭代数要比ICCG法的小很多。也就是说，径向基点插值型无单元多重节点法较ICCG法有更高的计算效率。

图5 总迭代数和收敛容差关系曲线

3 结 论

本文对于用多重节点法求解RPIM无单元法离散的电磁场域进行研究，总结如下:

(1)通过引入多重网格法的思想，构造了适用于径向基点插值型无单元法的多重节点法，并实现了用多重节点法求解径向基点插值型无单元法问题，从而在快速收敛的同时又兼有无单元法消除网格限制的特点。

(2)对同一问题来说，在相同的精度要求下，在同一自由度下，RPIM-MN法要较ICCG法具有更高的计算效率。

［1］ 张雄，宋康祖，陆明万.无网格法研究进展及其应用［J］.计算力学学报，2003，20(6):730-742.

［2］ Maréchal Y.Some meshless methods for electromagnetic field computations［J］.IEEE Trans.Mag.，1998，34(5):3351-3354.

［3］ Cingoski V，Miyamoto N，Yamashita H.Element-free Galerkin method for electromagnetic field Computations［J］.IEEE Trans.Mag.，1998，34(5):3236-3239.

［4］ 刘素贞，杨庆新，陈海燕，等.无单元法在电磁场数值计算中的应用研究［J］.电工技术学报.2001，16(2):30-33.

［5］ Lu Huifen，Jiang Hao.Application of meshless local Petrov-Galerkin methods in electromagnetics［C］//Electrical Machines and Systems.2003，2:798-801.

［6］ Ho S L，Yang S Y，Wong H C，et al.A meshless collocation method based on radial basis functions and wavelets［J］.IEEE Trans.Magn.，2004，40(2):1021-1024.

［7］ Li Gang，Aluru N R.Linear，nonlinear and mixed-regime analysis of electrostatic MEMS［J］.Sensor and Actuators(A)，2001，91(3):278-291.

［8］ Wang J G，Liu G R.A Point Interpolation Meshless Method Based on Radial Basis Functions［J］.Int.J.Numer.Methods Engrg.，2002，54:1623-1648.

［9］ Schaback R.Error estimates and condition numbers for radial basis function interpolation［J］.In Proceedings of Adv.Comput.Math.，1995:251-264.

［10］ Hackbusch W，Trottenberg U.Multigrid methods III［C］//Proc.3rd Int.Conf.on Multigrid methods.Int.Series of Num Math 98.Birkhauser，Basel 1991.

［11］ Hackbusch W，Trottenberg U.Multigrid methods［C］//Lecture Notes in Mathematics 960.Springer，Berlin，1986.

［12］ Iserles A.A first course in the numerical analysis of differential equations［M］.Cambridge:Cambridge Univ.Press，1996.

［13］ Hackbusch W.Convergence of multi-grid iterations applied to difference equation［J］.Math.Comp.，1980，34:425-440.

［14］ Hackbusch W.On the convergence of multi-grid iterations［J］.Beitrage Nuimer.Muth.，1981，9:213-239.

［15］ Hackbusch W，Wittum G.Multigrid methods V［C］//Proc.5th European Multigrid Conf.in Stuttgart Germany，Lecture Notes in Computational Science and Engineering 3.Springer，Berlin，1998.

［16］ Hackbusch W.Multi-grid methods and applications［M］.New York:Springer-Verlag，1985.

［17］ Hackbusch W，Trottenberg U.Multigrid methods II［C］//Lecture Notes in Mathematics 1228.Springer，Berlin，1982.

［18］ Hackbusch W.Robust multigrid methods［M］.Friedr Vieweg 8 Sohn，1988.

［19］ 周浩，倪光正.多重网格法及其在静态电磁场数值分析中的应用［J］.中国电机工程学报，1990，10(5):20-26.

［20］ Braess D，Verfurth R.Multigrid methods for nonconforming finite element methods［J］.IAM J.Numer.Anal.，1990，27:979-986.

［21］ 王立鹏，王欣彦，唐任远.EFG-MG法及其在电磁场数值计算中的应用［J］.电工技术学报.2010，25(1):1-5.