基于LMI和BMI的多时滞不确定离散系统稳定性凸优化算法
2013-02-19陈炎龙段红玉
陈炎龙,段红玉
CHEN Yan-long,DUAN Hong-yu
(河南牧业经济学院 信息工程系,郑州 450011)
0 引言
实际控制系统中产生的不确定性和时滞会降低系统的稳定性,这使得近十年来不确定时滞系统鲁棒控制研究倍受关注[1~3],在不确定离散多时滞系统的稳定性研究和成本界方面也取得了一些成果[4~6]。然而,基于LMI的不确定多时滞离散系统稳定性和可保成本方面的研究较少。最近,文献[7]利用线性矩阵不等式(LMI)解决了一类带有单输入输出时滞不确定系统的保成本控制,文献[8]推广了这一系统,获得了多时滞离散系统稳定性和可保成本的新LMI方法。真对文献[8],本文研究了基于LMI和BMI的多时滞不确定离散系统稳定性凸优化算法,以提高可保成本控制水平和获得较小下界。
1 相关基础知识
以如下不确定多时滞离散系统为例[8]:


针对系统(1),选取Lyapunov函数为:

其中,P>0,Si> 0, Tj >0。
定义1 对系统(1)和成本函数(2),如果存在状态反馈控制器u∗(k)和正数J∗,使得闭环系统(3)渐进稳定,且J ≤J∗,则称J∗为可保成本,u∗ (k)为保成本控制律。
引理1[8]给定矩阵D,E 和维数适当的对称矩阵G,对满足FT F ≤ I的矩阵F,不等式G+DFE+ETFT DT <0成立的充要条件是存在实数e>0 使得G+eD D T+e−1ET E<0。
2 所提系统稳定标准

则系统(3)是渐进稳定的,且可保成本:

证明 由公式(4)的Lyapunov函数V(x(k))沿公式(3)系统任意轨线的向前差分为:

令,η(k)=(xT(k),xT(k−τ))T,将公式(7)中
i第二项改写为:

因此:

根据Lyapunov稳定理论,公式(3)的系统是渐进稳定的。
不等式(8)表明:
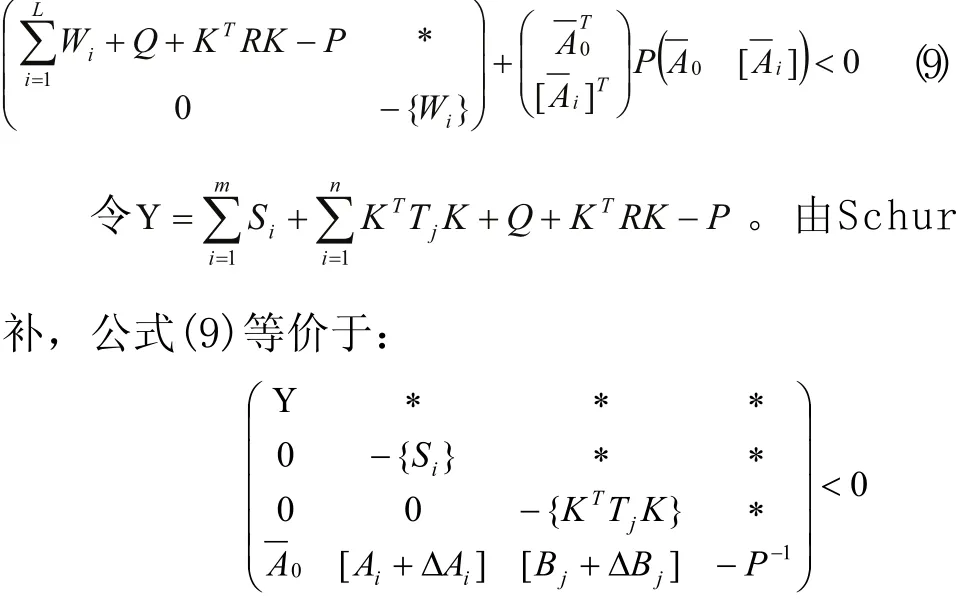
上式可以改写成:
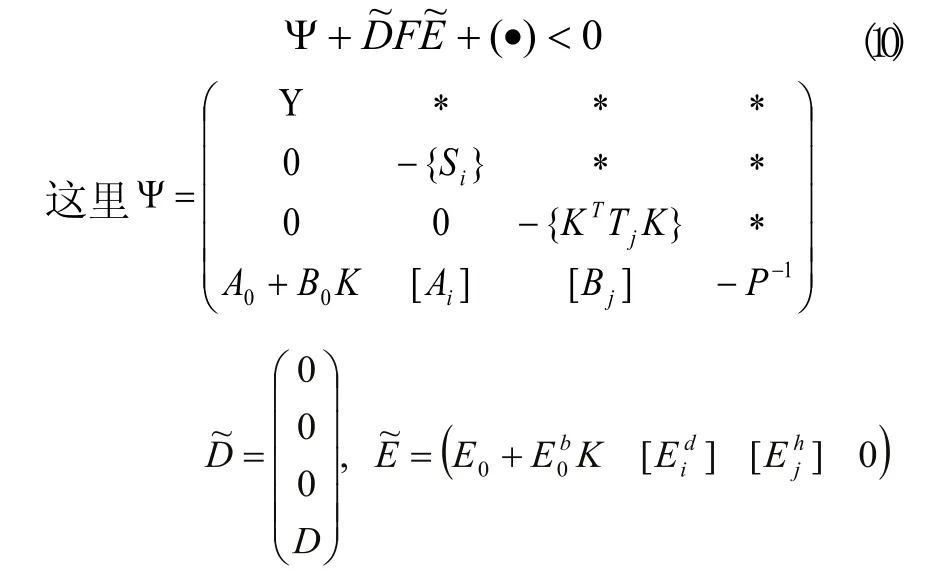
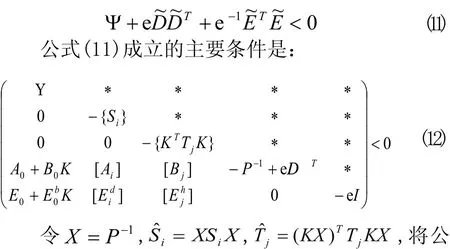
据引理,公式(10)成立当且仅当存在实数e >0使得下式成立:式(12)边同时乘以diag(X,{X m },{X n },I,I),再次利用Schur complement引理,公式(12)与公式(5)等价。而且,由公式(7)式得到:
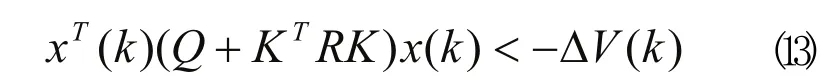
将公式(13)两边从0到∞求和,结合系统稳定性,就有:

3 所提相关凸优化算法

注3:本算法依赖于初始可行解,在不等式(6)有可行解得情况下,算法可能求不到解.但是如果初始可行解满足算法,由于它考虑解的迭代搜索,使得获得的近优解具有较少的保守性。
4 实例验证
考虑不确定多时滞离散系统[8]:

K=(−0.0363,−0.0459,−0.0132).相应于(6)式的可保成本J *=16.5445,小于文献[8]中的J *=18.5931。
5 结束语
本文研究了多时滞不确定离散系统的稳定性,给出了一个系统稳定定理,并基于LMI和BMI,提出了一个相关稳定性凸优化算法,同文献[8]的方法相比,本文优化算法能够获得较小的可保成本。
[1]K.Ramakrishnan,G.Ray.Robust stability criteria for a class of uncertain discrete-time systems with time-varying delay[J].Applied Mathematical Modelling,2013,37(3):1468-1479.
[2]Duyu Liu,Shouming Zhong,Xinzhi Liu.Stability analysis for uncertain switched neutral systems with discrete timevarying delay:A delay-dependent method[J].Mathematics and Computers in Simulation,2009,80(2):436-448.
[3]吴江江,余世明.一类不确定多时滞离散系统的稳定性分析与鲁棒控制器设计[J].自动化技术与应用,2010,29(1):1-3.
[4]罗跃生,龚新平,李彤.离散多时滞系统时滞记忆鲁棒H∞容错控制[J].华中科技大学学报(自然科学版),2011,30(11):61-67.
[5]Z.Q.Zuo.Y.J.Wang.Novel Optimal Guaranteed Cost Control of Uncertain Discrete Systems with Both State and Input Delays[J].Journal of Optimization Theory and Appli cations,2008,139(10):159-170.
[6]Zhang,Tang.Output feedbackH∞control for uncertain piecewise linear systems[J].Journal of Dynamical and Control Systems,2008,l4(1):141-144.
[7]李阳.多时滞离散系统的反馈控制器设计[J].科学技术与工程,2012,12(31):8434-8437.
[8]杨晓娜,吴华滨,林小峰.基于HDP的离散多时滞系统的优化控制[J].计算机测量与控制,2013,21(2):388-290.
